INST 240 Revolutions Lecture 8 Spacetime Diagrams Cause

INST 240 Revolutions Lecture 8 Spacetime Diagrams

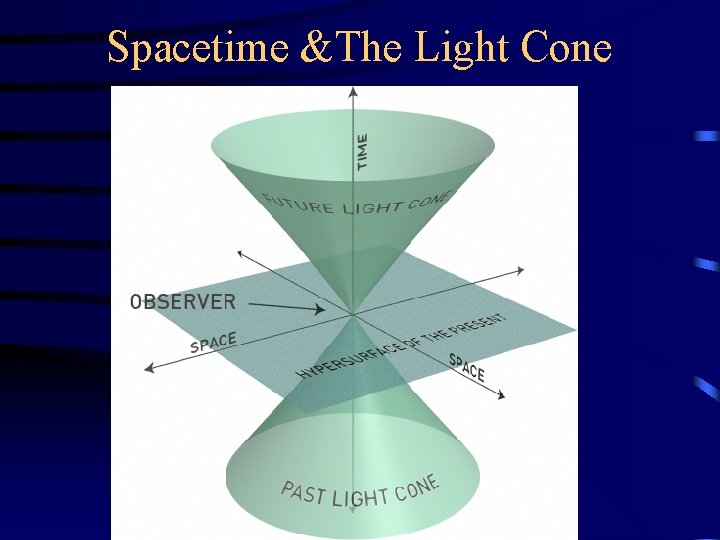
Cause and Effect • How does relativity ensure that some events appear in the “correct” order, while for others it doesn’t matter? • We’ll see later that these events are in different categories (space-like and timelike connected) • It will be easy to figure out which is which with the help of a light-cone diagram

Spacetime &The Light Cone

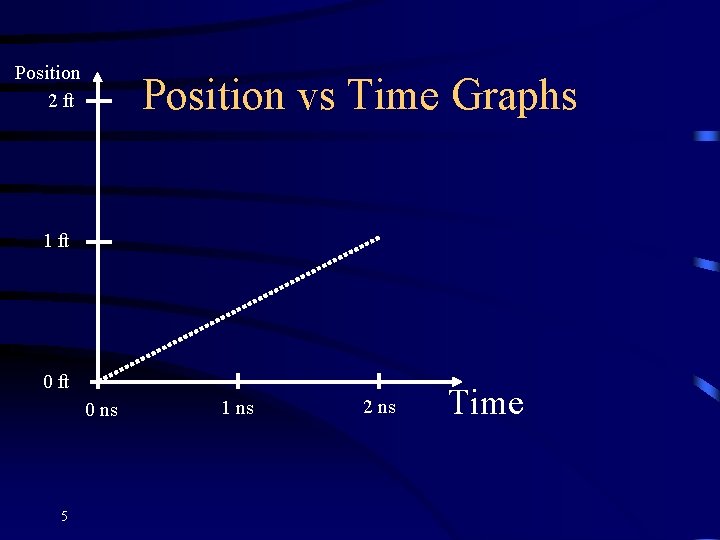
Position 2 ft Position vs Time Graphs 1 ft 0 ns 5 1 ns 2 ns Time

Spacetime graphs (Axes flipped) Time Space (Position) 6

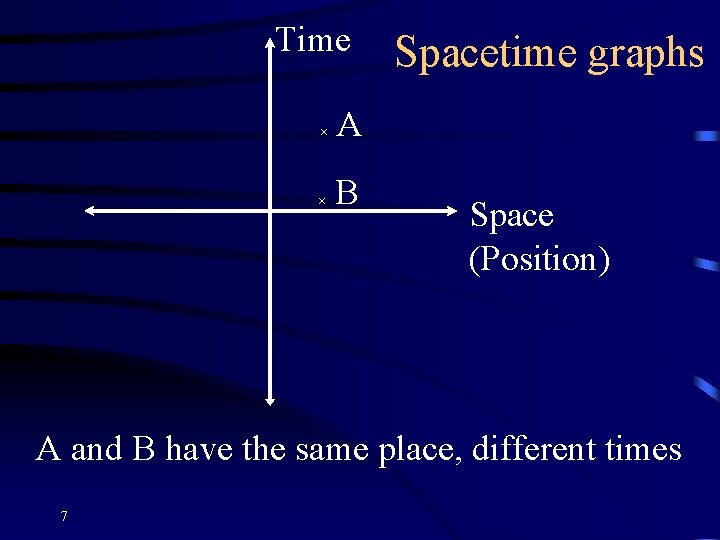
Time × × Spacetime graphs A B Space (Position) A and B have the same place, different times 7

Time × A × Spacetime graphs B Space (Position) Everybody snap your fingers like this. 8

Time × × A Spacetime graphs B Space (Position) Everybody snap your fingers like this 9

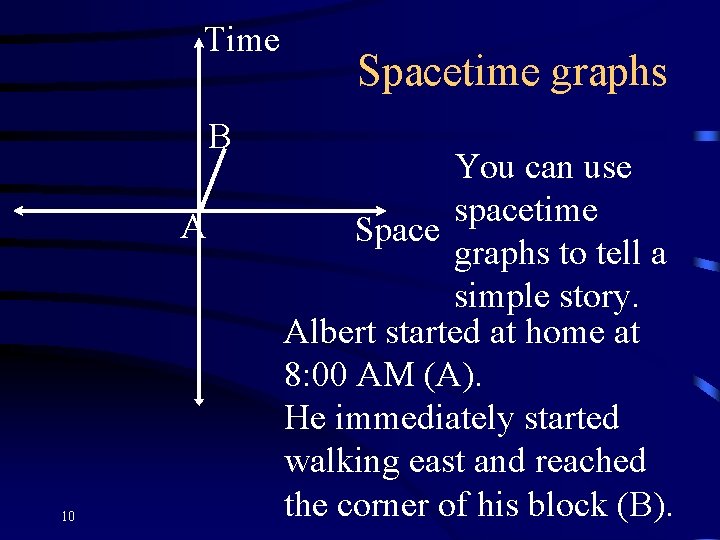
Time B A 10 Spacetime graphs You can use spacetime Space graphs to tell a simple story. Albert started at home at 8: 00 AM (A). He immediately started walking east and reached the corner of his block (B).

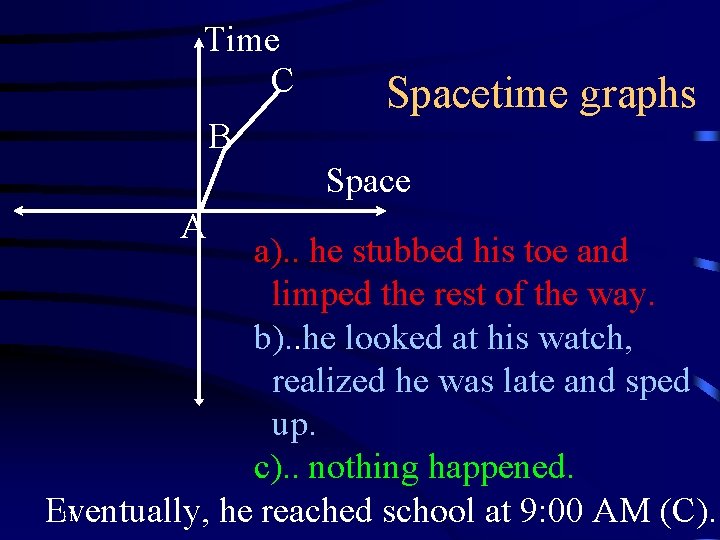
Time C B Spacetime graphs Space A a). . he stubbed his toe and limped the rest of the way. b). . he looked at his watch, realized he was late and sped up. c). . nothing happened. Eventually, he reached school at 9: 00 AM (C). 11

Spacetime = Space plus Time • In relativity space and time are not independent of each other (if one is measured differently by a second observer, so is the other) • Makes sense to upgrade time to a direction (dimension) rather than viewing it as an (unchanging) parameter

Worksheet Part 1 • Make up stories using the space-time diagrams 13

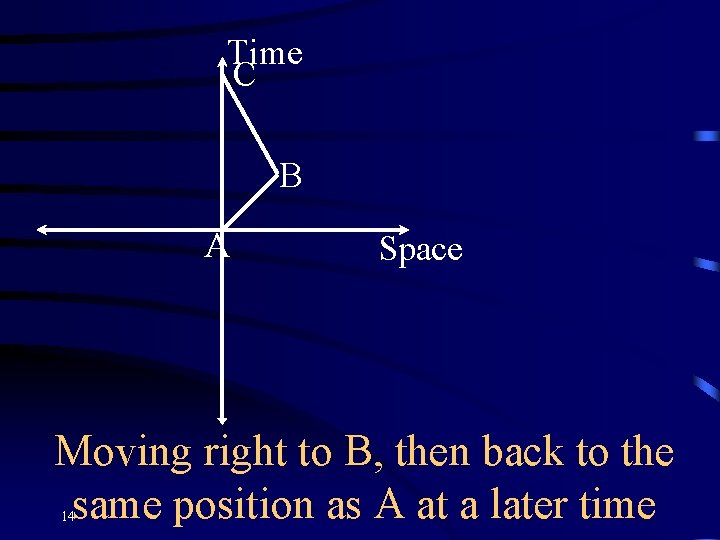
Time C B A Space Moving right to B, then back to the same position as A at a later time 14

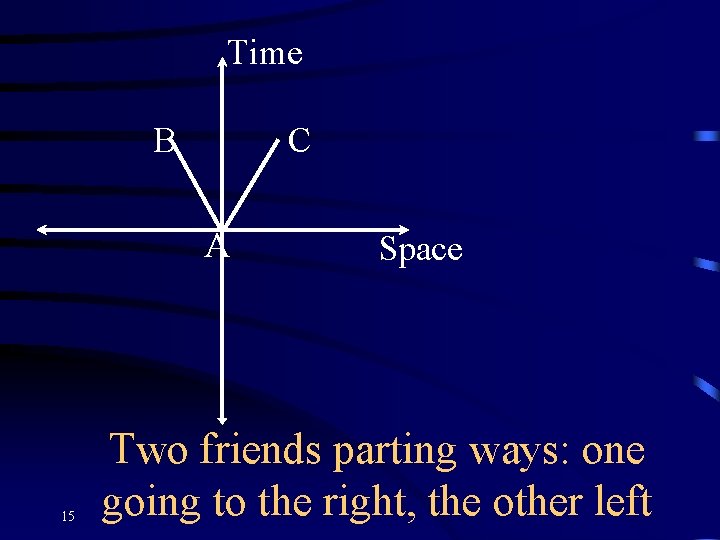
Time B C A 15 Space Two friends parting ways: one going to the right, the other left

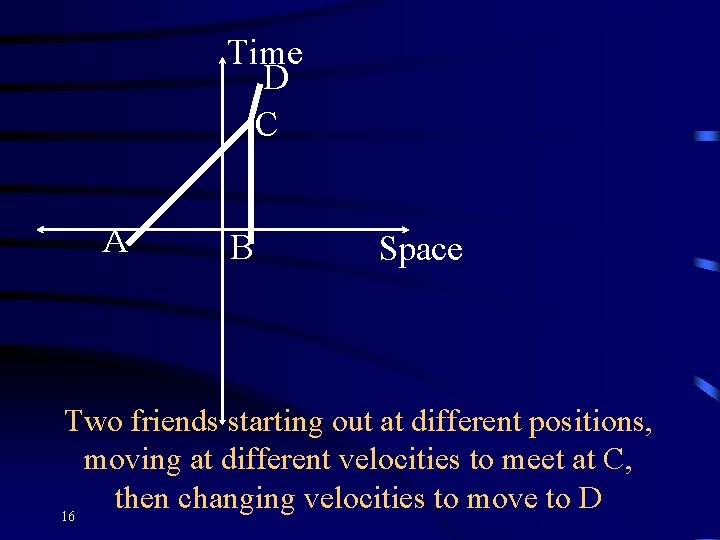
Time D C A B Space Two friends starting out at different positions, moving at different velocities to meet at C, then changing velocities to move to D 16

What is ct? • Skippyjon Jones The units for 'c' are meters/second. The units for 't' are seconds. When these two units are multiplied, we are simply left with meters. (m/s)(s)=m. 'ct' is used to represent distance in time. • Somebody In this expression, 'ct' would be represented by meters in spacetime. This 'c' represents the cosmic speed, which can be considered the speed of light, and 't' is time. Therefore, 'ct' could be used to represent the distance in spacetime.

ct What is this (ct) means c times t t is in seconds thing? ct is in meters So c is in meters/second If t = 1 second, (ct) = 3 x 108 m/s x 1 s = 3 x 108 m We can say “the time was 300 000 meters” instead of “the time was 1 second” 18

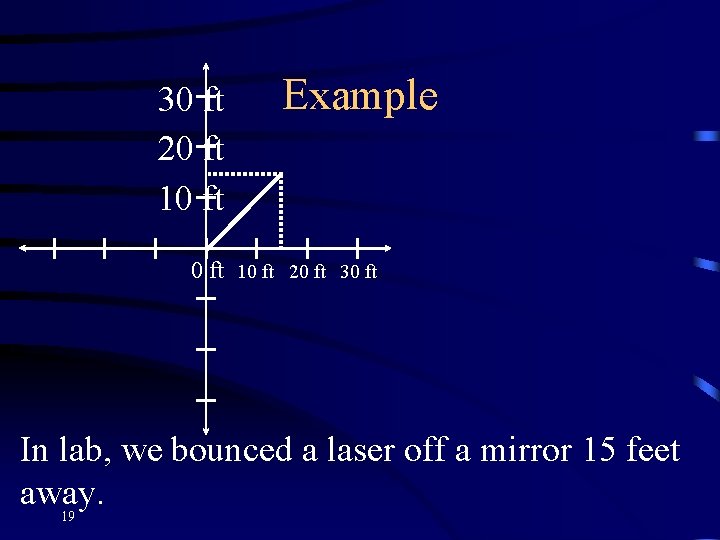
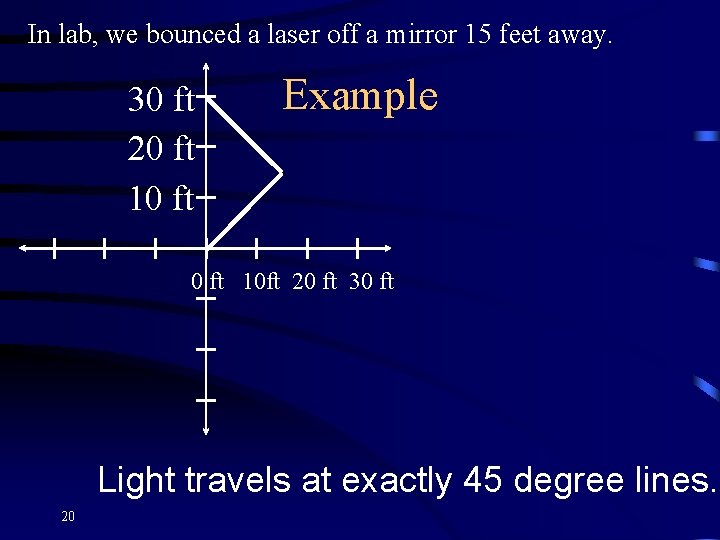
30 ft 20 ft 10 ft Example 0 ft 10 ft 20 ft 30 ft In lab, we bounced a laser off a mirror 15 feet away. 19

In lab, we bounced a laser off a mirror 15 feet away. 30 ft 20 ft 10 ft Example 0 ft 10 ft 20 ft 30 ft Light travels at exactly 45 degree lines. 20

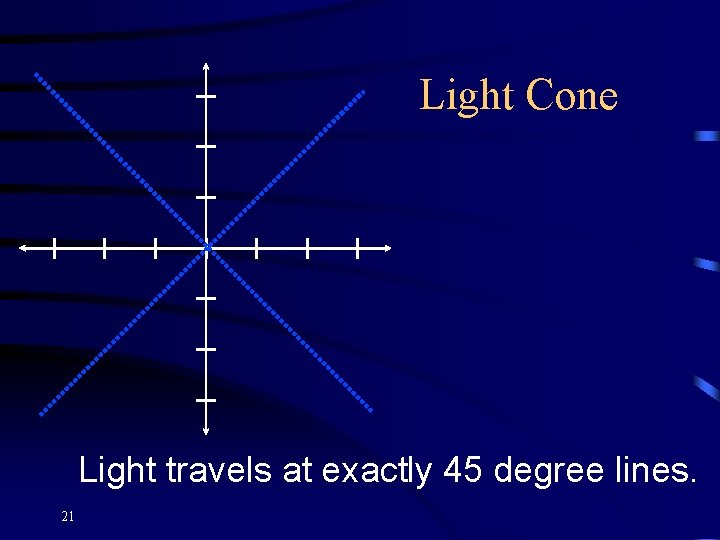
Light Cone Light travels at exactly 45 degree lines. 21

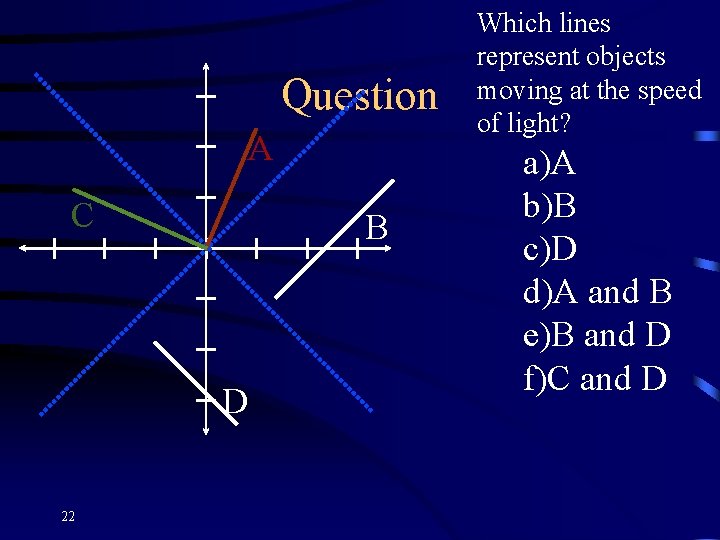
Question A C B D 22 Which lines represent objects moving at the speed of light? a)A b)B c)D d)A and B e)B and D f)C and D

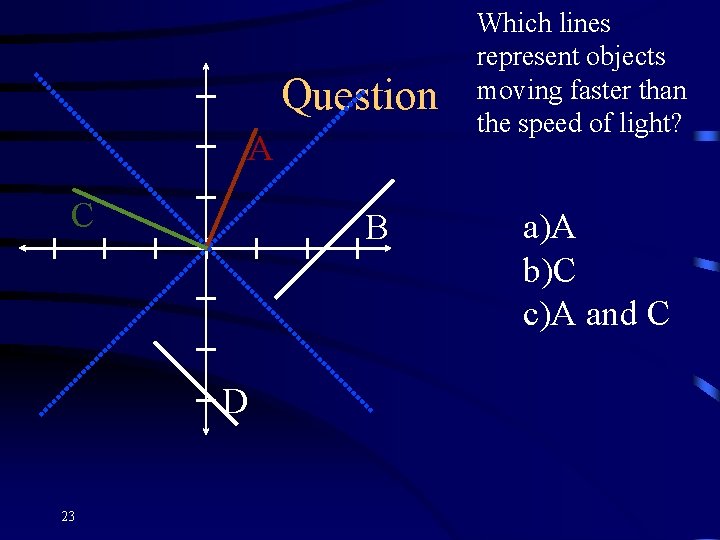
Question A C B D 23 Which lines represent objects moving faster than the speed of light? a)A b)C c)A and C

Worksheet II • Label both axes with the right units • Draw the spacetime graphs for the stories 24

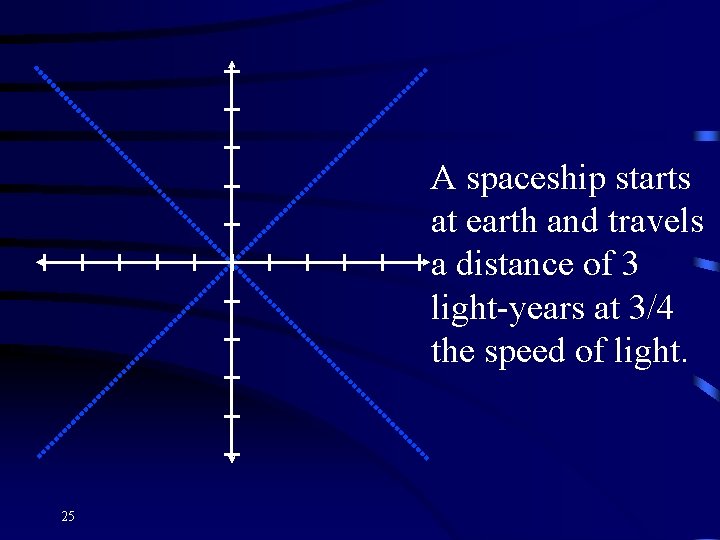
A spaceship starts at earth and travels a distance of 3 light-years at 3/4 the speed of light. 25

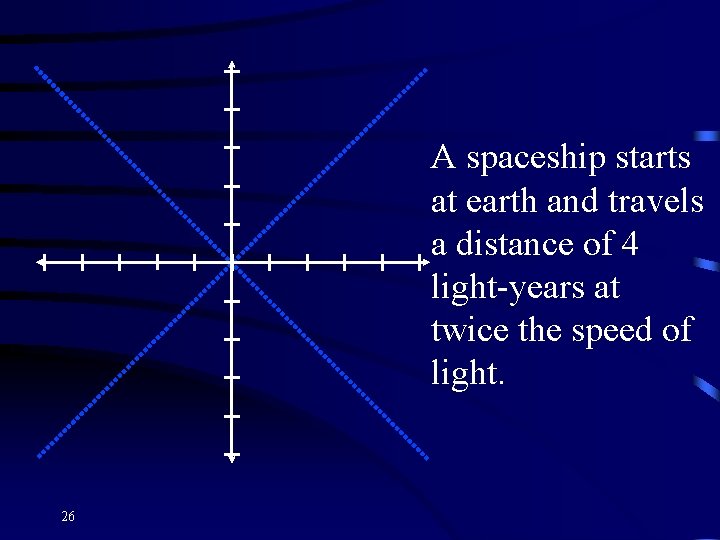
A spaceship starts at earth and travels a distance of 4 light-years at twice the speed of light. 26

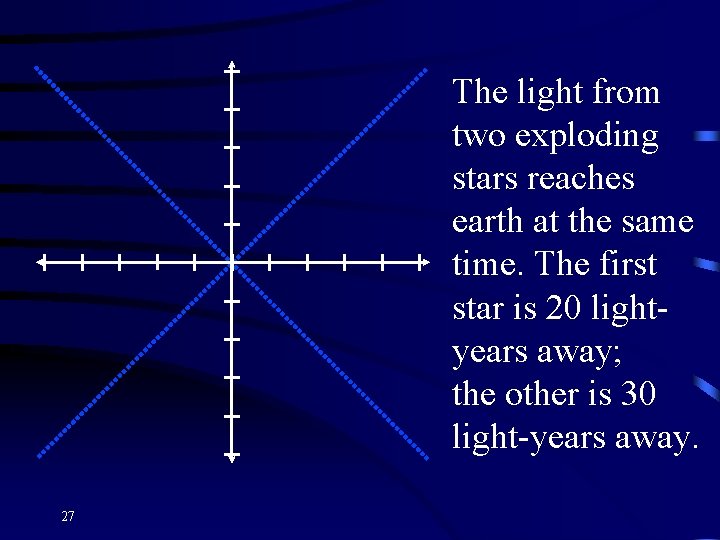
The light from two exploding stars reaches earth at the same time. The first star is 20 lightyears away; the other is 30 light-years away. 27

Cosmic speed limit So far, scientists have not observed any phenomenon that moves faster than the speed of light. This includes any form of communication or information transit. Later we will see WHY we think this to be universally true, but let’s just take it as a fact for the moment. 28

×O 29 We are here and now

×A ×O 30 We can walk or send a rocket or a message from O to A, so we can affect it. (Nostradamus sending a letter to start the Great Fire of London)

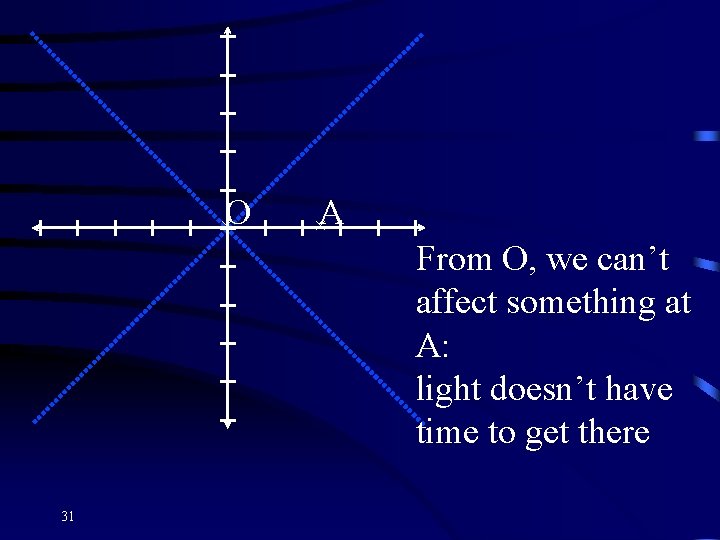
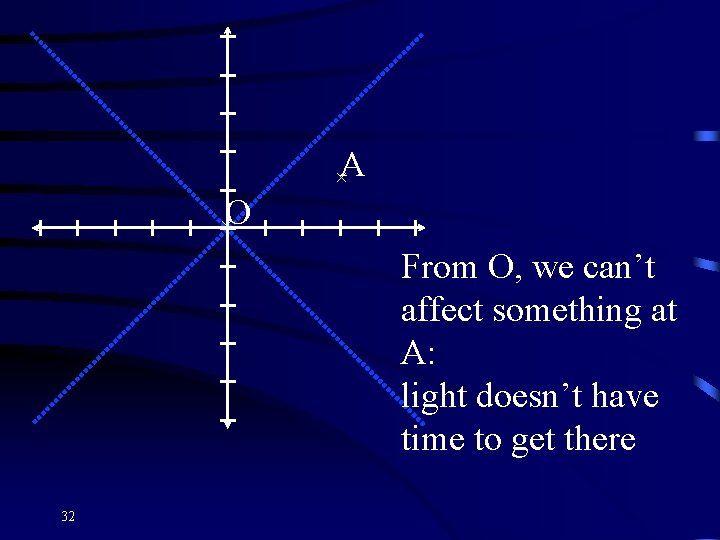
×O 31 ×A From O, we can’t affect something at A: light doesn’t have time to get there

×A ×O From O, we can’t affect something at A: light doesn’t have time to get there 32

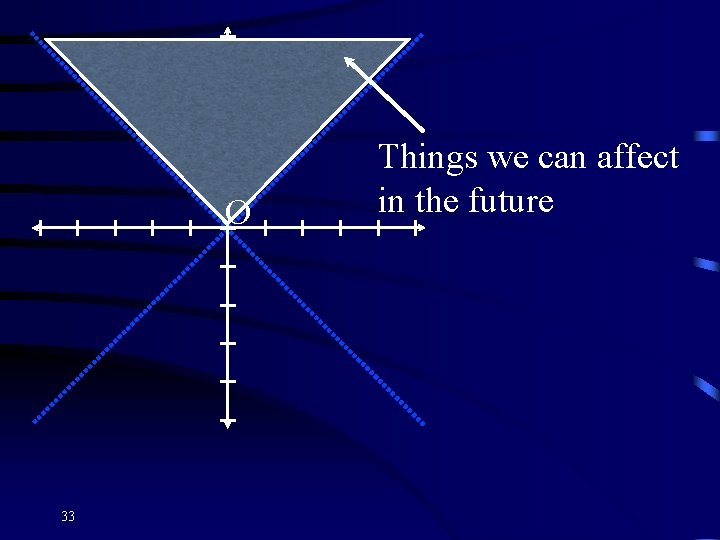
×O 33 Things we can affect in the future

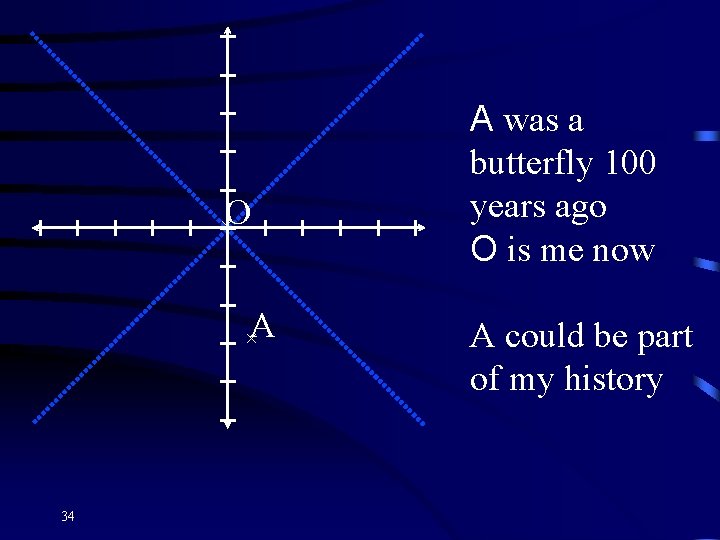
×O ×A 34 A was a butterfly 100 years ago O is me now A could be part of my history

A happened in the past O is me now ×O ×A But I can’t possibly know A has happened. . . light from A hasn’t reached me yet. e. g. a star 100 light years away exploded 50 years ago. 35

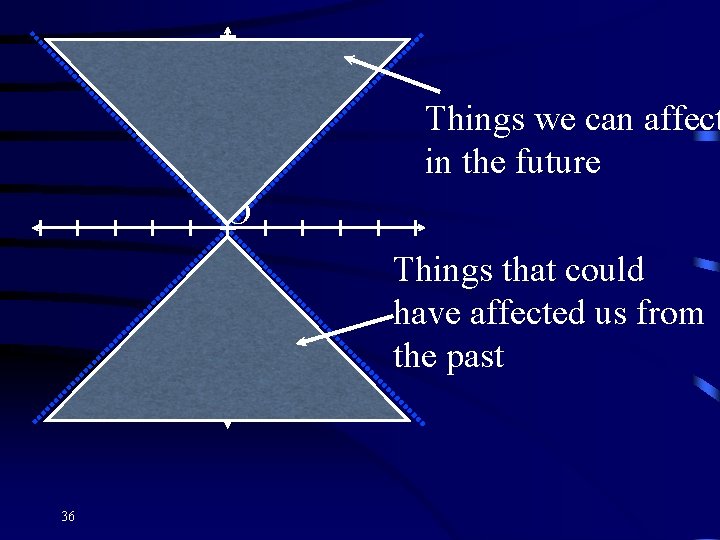
Things we can affect in the future ×O Things that could have affected us from the past 36

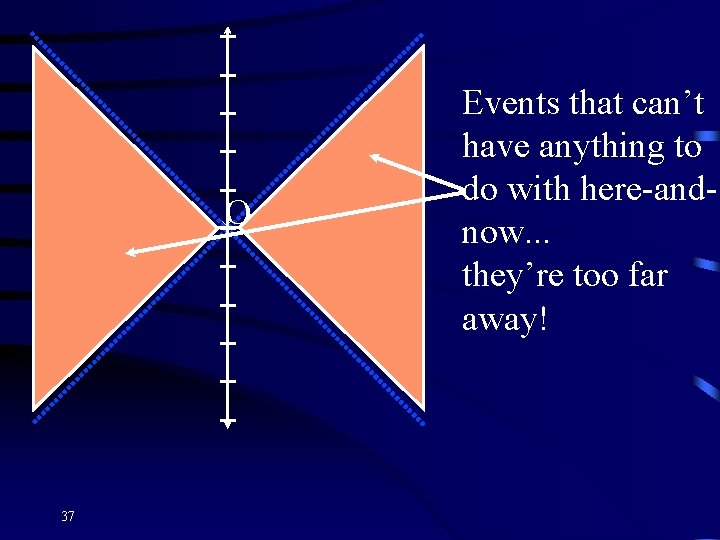
×O 37 Events that can’t have anything to do with here-andnow. . . they’re too far away!

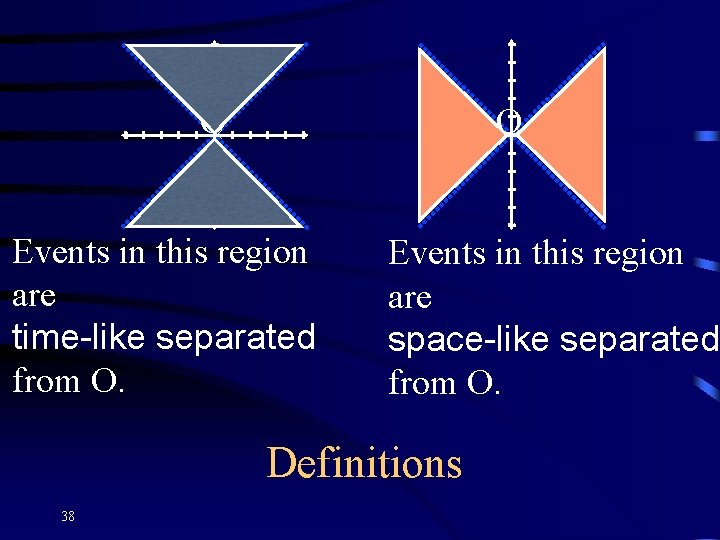
O× O× Events in this region are time-like separated from O. Events in this region are space-like separated from O. Definitions 38

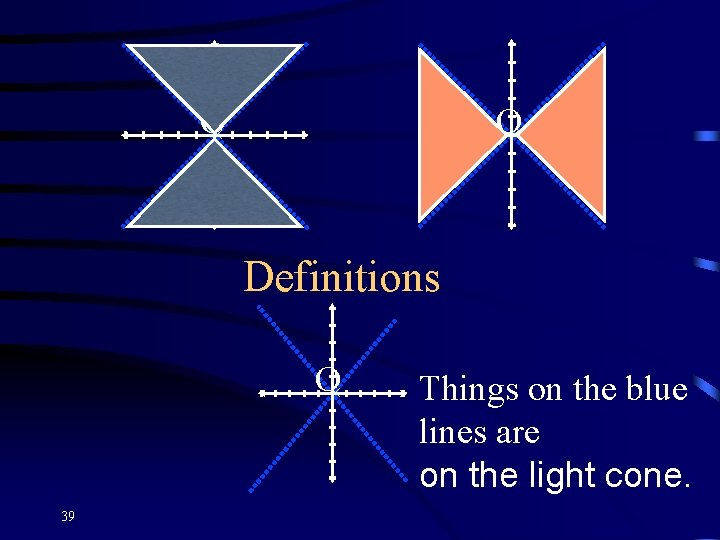
O× O× Definitions O× 39 Things on the blue lines are on the light cone.

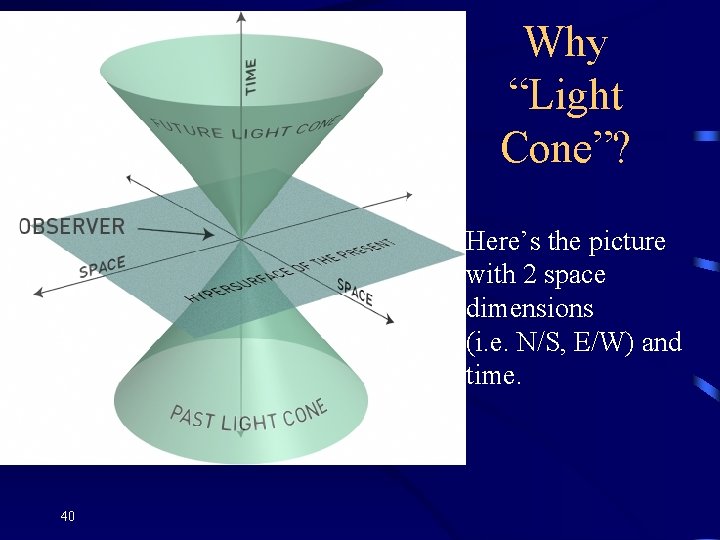
Why “Light Cone”? Here’s the picture with 2 space dimensions (i. e. N/S, E/W) and time. 40

Invariants: totally constant • are 65 adfg 5 h 4634 An invariant quantity is a value which is unchanged when applied to a different coordinate system. An example of an invariant quantity would be the distance between two points on a line. • Mikey Cigars Laws of nature will not change no matter what your viewing point is. For example, a TV will work in the family room of your house just the same as if it were in the kitchen. Two different places does not change the result.

Invariants • Observers can disagree on many things (distances, time intervals) • Can they agree on something? – Speed of light – Physics – Invariants!

How do we construct an invariant? • Pragmatic way: see what stuff (physics) we have to agree on, then express them in terms of the quantities we do not have agree on (coordinates) • Often, invariants are connected to symmetries

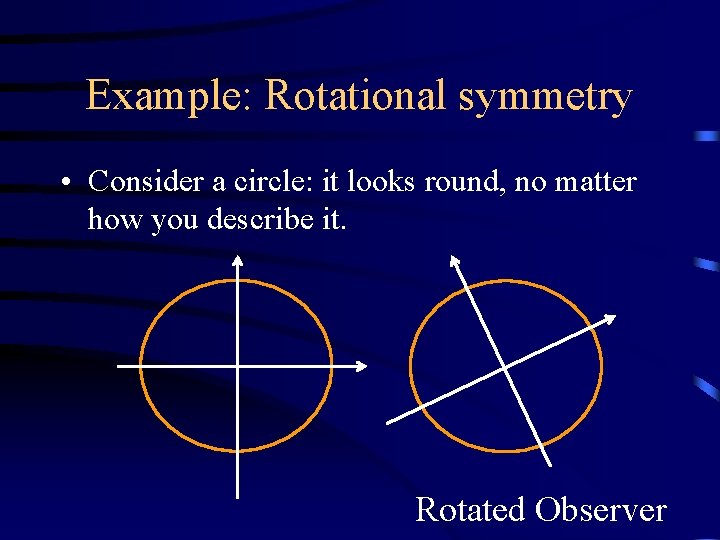
Example: Rotational symmetry • Consider a circle: it looks round, no matter how you describe it. Rotated Observer

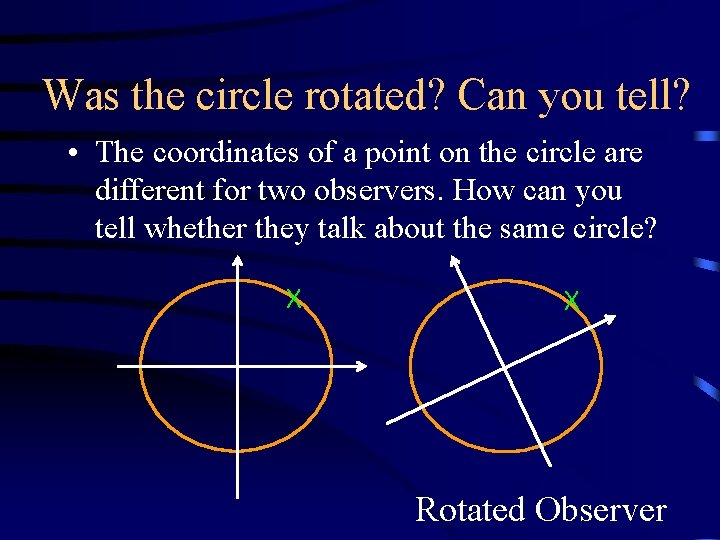
Was the circle rotated? Can you tell? • The coordinates of a point on the circle are different for two observers. How can you tell whether they talk about the same circle? x x Rotated Observer

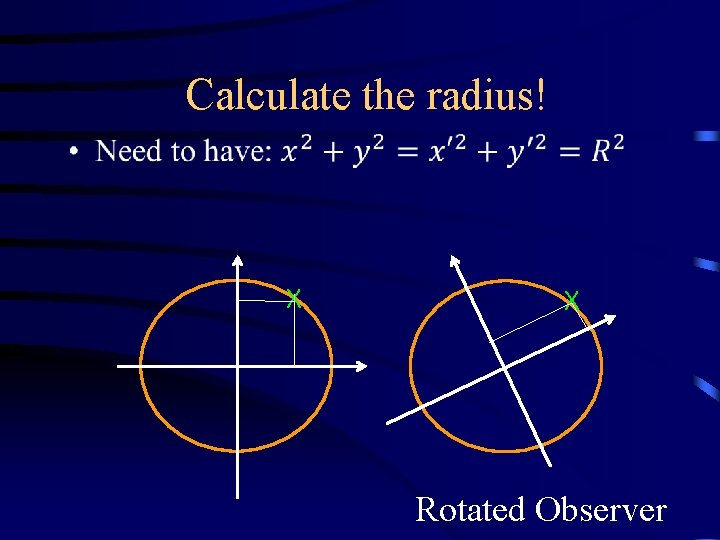
Calculate the radius! • x x Rotated Observer

Every observer has to agree on the radius; it’s what makes this circle! • The radius of the circle is an invariant – It stems from rotational symmetry

Pythagoras doesn’t work in Relativity! • See textbook: the “geometry” of spacetime is not as simple as the geometry of a flat sheet of paper (euclidean geometry, aka the geometry where Pythagoras works, the sum of the angles of a triangle is 180 degrees, etc. )

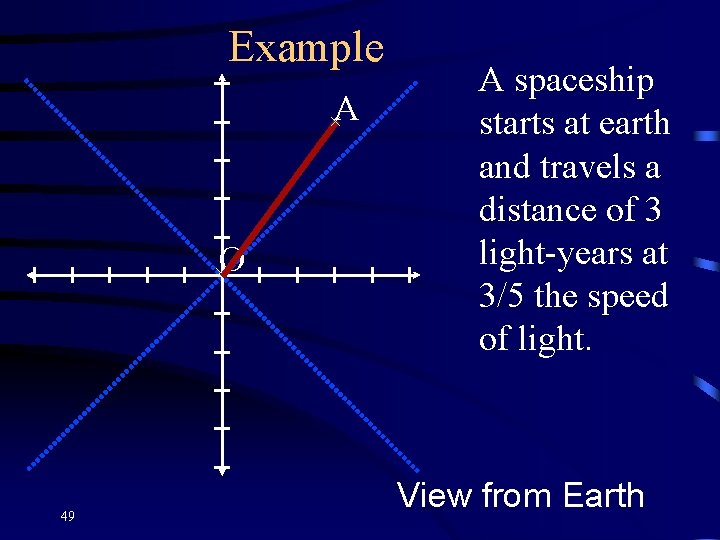
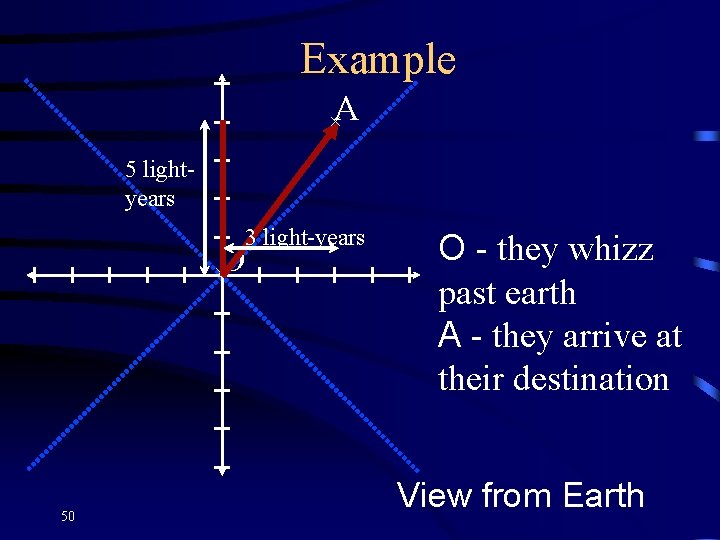
Example ×A ×O 49 A spaceship starts at earth and travels a distance of 3 light-years at 3/5 the speed of light. View from Earth

Example ×A 5 lightyears ×O 50 3 light-years O - they whizz past earth A - they arrive at their destination View from Earth

Gamma etc. if v/c = 3/5 c then γ = 5/4=1. 25 c. T’ = proper time = “c time” seen from rocket = 4 light-years View from Rocket 51

View from Rocket L’ = proper distance = distance seen from earth = 3 light-years L = contracted distance = L’/γ = 3 light-years/1. 25 = 12/5 ly = 2. 4 light-years 52

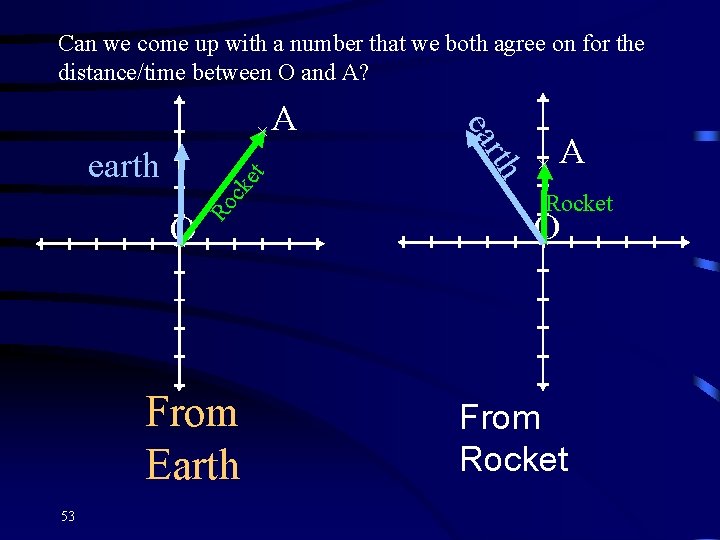
Can we come up with a number that we both agree on for the distance/time between O and A? ck et Ro O × From Earth 53 th ear ×A × A Rocket O × From Rocket

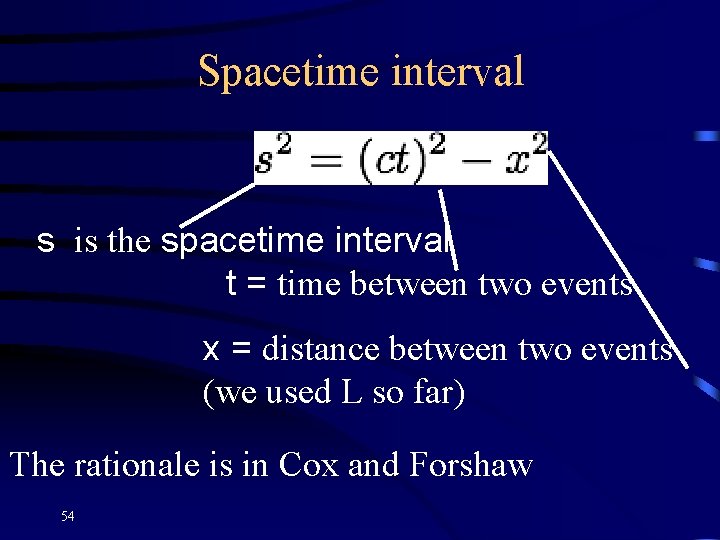
Spacetime interval s is the spacetime interval t = time between two events x = distance between two events (we used L so far) The rationale is in Cox and Forshaw 54

O-A measured by earth: t = 5 years so, ct = 5 light-years x = 3 light-years s 2 = (ct)2 - x 2 s 2 = (5)2 - (3)2 s 2 = 25 - 9 = 16 s = 4 light-years O-A measured by rocket: t = 4 years so, ct = 4 light-years x = 0 light-years (rocket doesn’t move) s 2 = (ct)2 - x 2 s 2 = (4)2 - (0)2 s 2 = 16 - 0 = 16 s = 4 light-years That is. . . s is just another name for the proper time! 55

The invariant! Every observer will calculate the same number: s = 4 light-years between the rocket leaving and the rocket arriving.

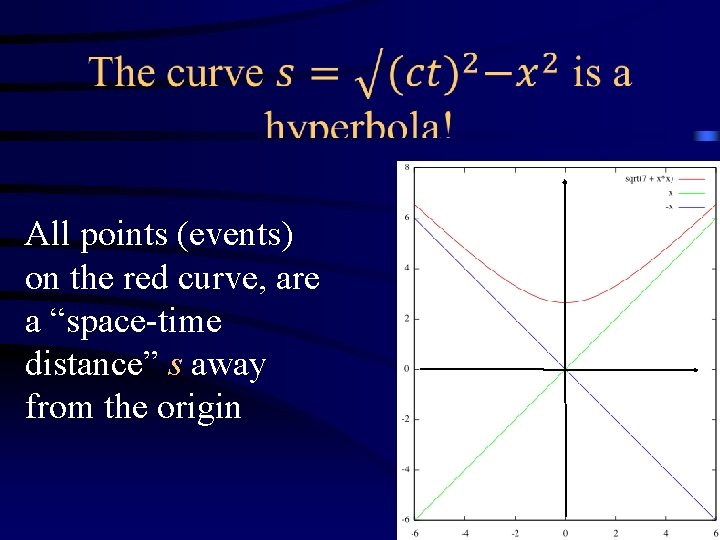
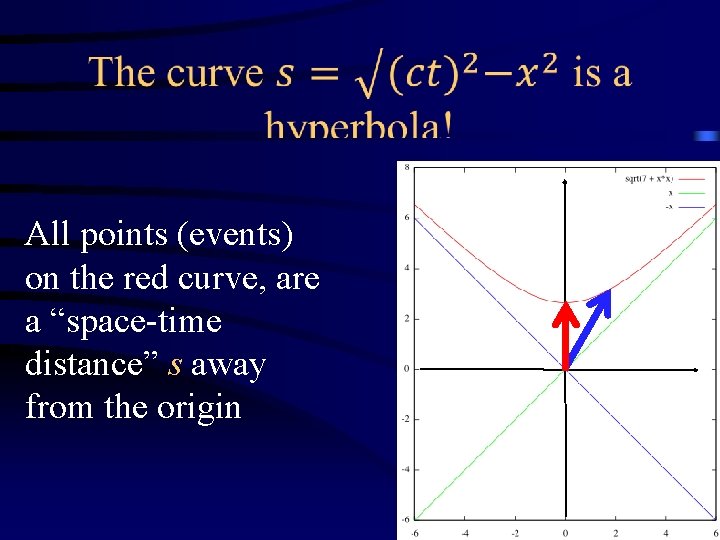
All points (events) on the red curve, are a “space-time distance” s away from the origin

All points (events) on the red curve, are a “space-time distance” s away from the origin