Insensitivity of GNSS to geocenter motion through the

Insensitivity of GNSS to geocenter motion through the network shift approach Paul Rebischung, Zuheir Altamimi, Tim Springer AGU Fall Meeting 2013, San Francisco, December 9 -13, 2013 1

Observing geocenter motion with GNSS • Degree-1 deformation approach (Blewitt et al. , 2001): – Based on the fact that loading-induced geocenter motion is accompanied by deformations of the Earth’s crust. – Gives satisfying results. – But can only sense non-secular, loading-induced geocenter motion. • Network shift approach: – Weekly AC solutions theoretically CM-centered. – AC → ITRF translations should reflect geocenter motion. – But unlike SLR, GNSS have so far not proven able to reliably observe geocenter motion through the network shift approach. – Why? 2

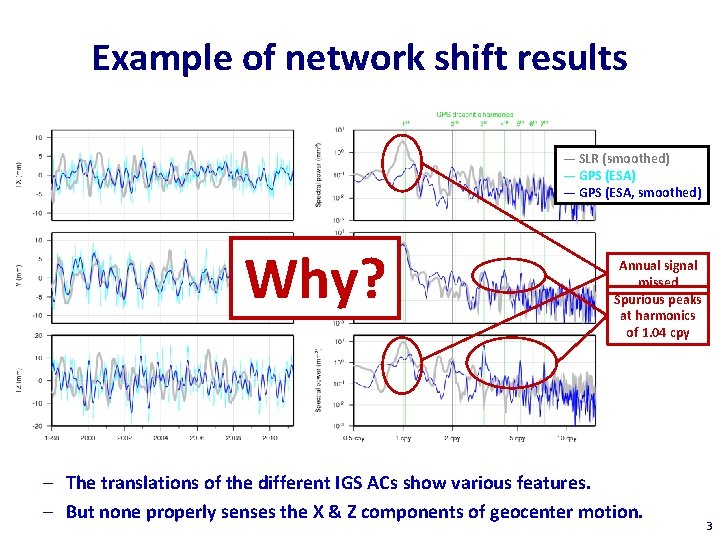
Example of network shift results — SLR (smoothed) — GPS (ESA, smoothed) Why? Annual signal missed Spurious peaks at harmonics of 1. 04 cpy – The translations of the different IGS ACs show various features. – But none properly senses the X & Z components of geocenter motion. 3

(Multi-) Collinearity • Consider the linear regression model: y = Ax + v = Σ Aixi + v observations parameters residuals – Ai = ∂y / ∂xi = « signature » of xi on the observations • Collinearity = existence of quasi-dependencies among the Ai’s • Consequences: – Some (linear combinations of) parameters cannot be reliably inferred, – are extremely sensitive to any modeling or observation error, – have large formal errors. 4

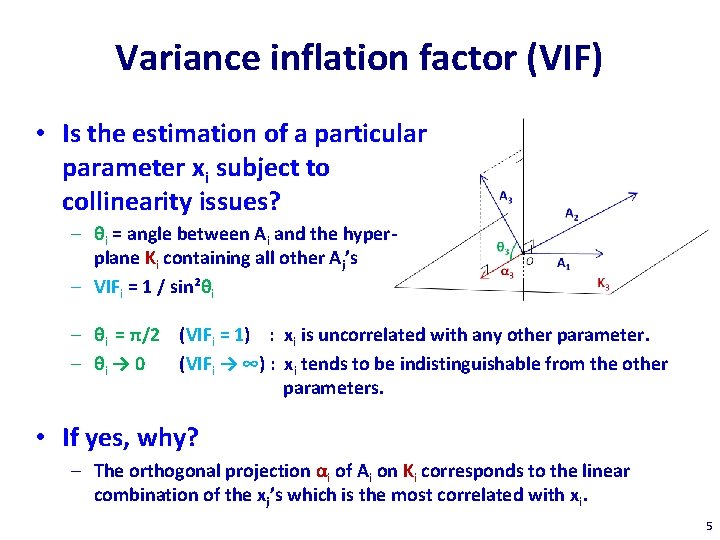
Variance inflation factor (VIF) • Is the estimation of a particular parameter xi subject to collinearity issues? – θi = angle between Ai and the hyperplane Ki containing all other Aj’s – VIFi = 1 / sin²θi – θi = π/2 (VIFi = 1) : xi is uncorrelated with any other parameter. – θi → 0 (VIFi → ∞) : xi tends to be indistinguishable from the other parameters. • If yes, why? – The orthogonal projection αi of Ai on Ki corresponds to the linear combination of the xj’s which is the most correlated with xi. 5

Mathematical difficulties • Geocenter coordinates are not explicitly estimated parameters. – They are implicitly realized through station coordinates. → Extend previous notions to such « implicit parameters » . • There are perfect orientation singularities. → Extend previous notions so as to handle singularities supplemented by minimal constraints. • The whole normal matrix is not available. – Clock parameters are either reduced or annihilated by forming double-differenced observations. → Practical collinearity diagnosis (next slide) 6

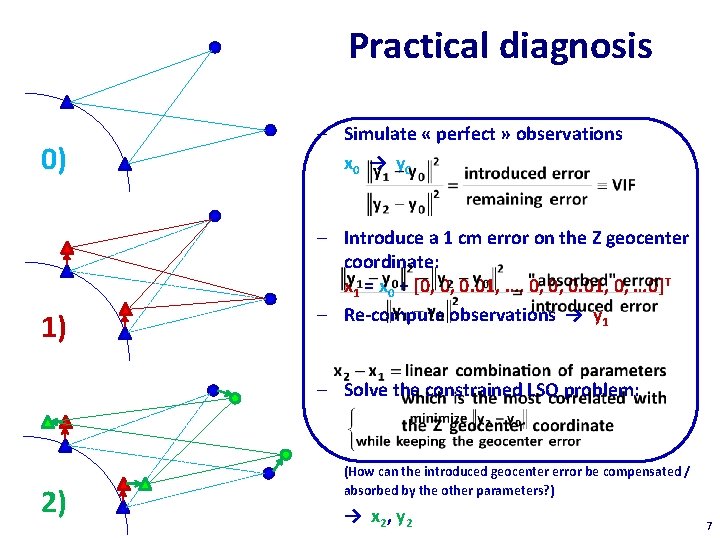
Practical diagnosis 0) 1) – Simulate « perfect » observations x 0 → y 0 – Introduce a 1 cm error on the Z geocenter coordinate: x 1 = x 0 + [0, 0, 0. 01, …, 0, 0, 0. 01, 0, … 0]T – Re-compute observations → y 1 – Solve the constrained LSQ problem: 2) (How can the introduced geocenter error be compensated / absorbed by the other parameters? ) → x 2, y 2 7

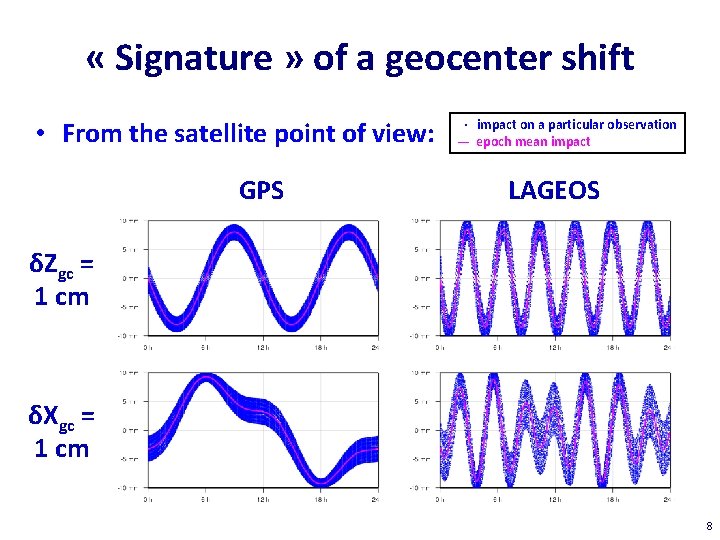
« Signature » of a geocenter shift • From the satellite point of view: GPS · impact on a particular observation — epoch mean impact LAGEOS δZgc = 1 cm δXgc = 1 cm 8

1 st issue: satellite clock offsets • Satellite clocks ↔ constant per epoch and satellite → The epoch mean geocenter signature is 100% absorbable by (indistinguishable from) the satellite clock offsets. → The GNSS geocenter determination can only rely on a 2 nd order signature. • In case of SLR : – The epoch mean signatures of Xgc and Ygc are directly observable. → No collinearity issue for Xgc and Ygc (VIF ≈ 1) – The epoch mean signature of Zgc is absorbable by the satellite osculating elements. → Slight collinearity issue for Zgc (VIF ≈ 9) 9

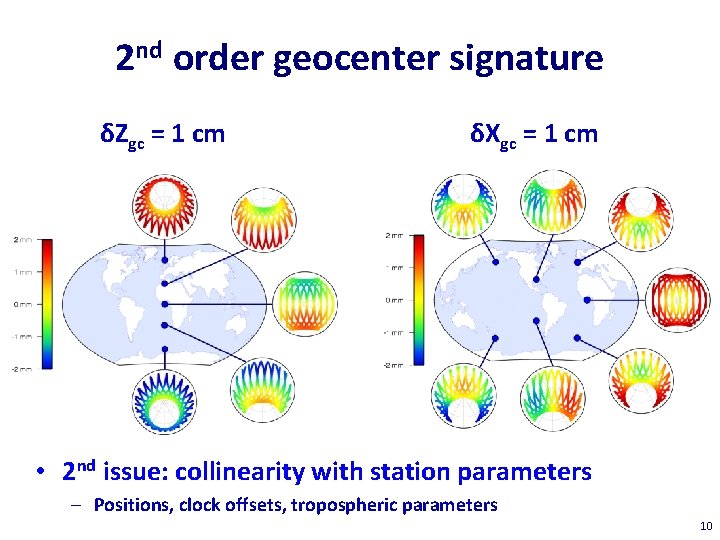
2 nd order geocenter signature δZgc = 1 cm δXgc = 1 cm • 2 nd issue: collinearity with station parameters – Positions, clock offsets, tropospheric parameters 10

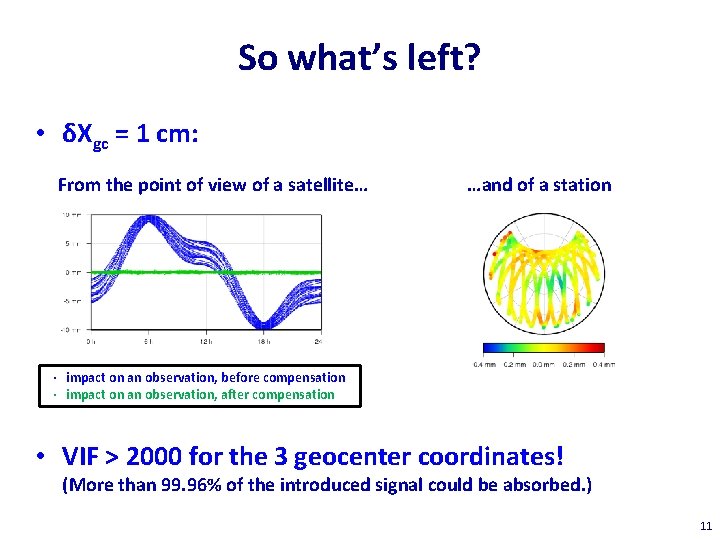
So what’s left? • δXgc = 1 cm: From the point of view of a satellite… …and of a station · impact on an observation, before compensation · impact on an observation, after compensation • VIF > 2000 for the 3 geocenter coordinates! (More than 99. 96% of the introduced signal could be absorbed. ) 11

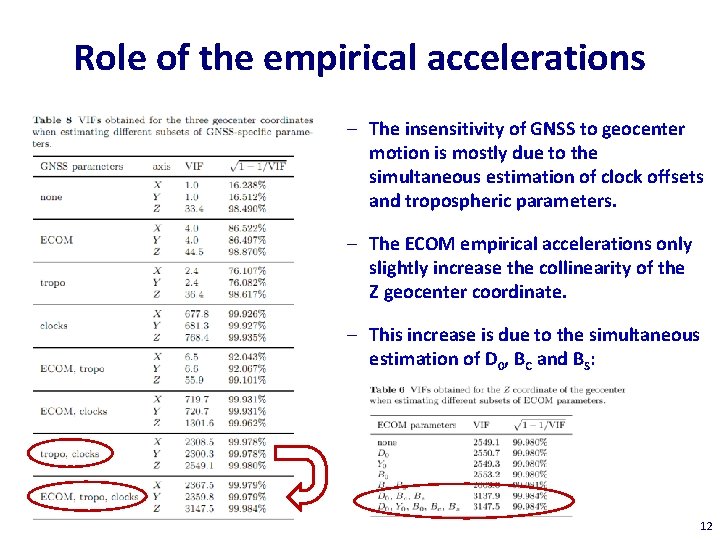
Role of the empirical accelerations – The insensitivity of GNSS to geocenter motion is mostly due to the simultaneous estimation of clock offsets and tropospheric parameters. – The ECOM empirical accelerations only slightly increase the collinearity of the Z geocenter coordinate. – This increase is due to the simultaneous estimation of D 0, BC and BS: 12

Conclusions (1/2) • Current GNSS are barely sensitive to geocenter motion. – The 3 geocenter coordinates are extremely collinear with other GNSS parameters, especially satellite clock offsets and all station parameters. – Their VIFs are huge (at the same level as for the terrestrial scale when the satellite z-PCOs are estimated). – The GNSS geocenter determination can only rely on a tiny 3 rd order signal. – Other parameters not considered here (unfixed ambiguities) probably worsen things even more (cf. GLONASS). 13

Conclusions (2/2) • The empirical satellite accelerations do not have a predominant role. – Contradicts Meindl et al. (2013)’s conclusions • What can be done? – Reduce collinearity issues (highly stable satellite clocks? ) – Reduce modeling errors (radiation pressure, higher-order ionosphere…) – Continue to rely on SLR… 14

Thanks for your attention! For more: Rebischung P, Altamimi Z, Springer T (2013) A collinearity diagnosis of the GNSS geocenter determination. Journal of Geodesy. DOI: 10. 1007/s 00190 -013 -0669 -5 15

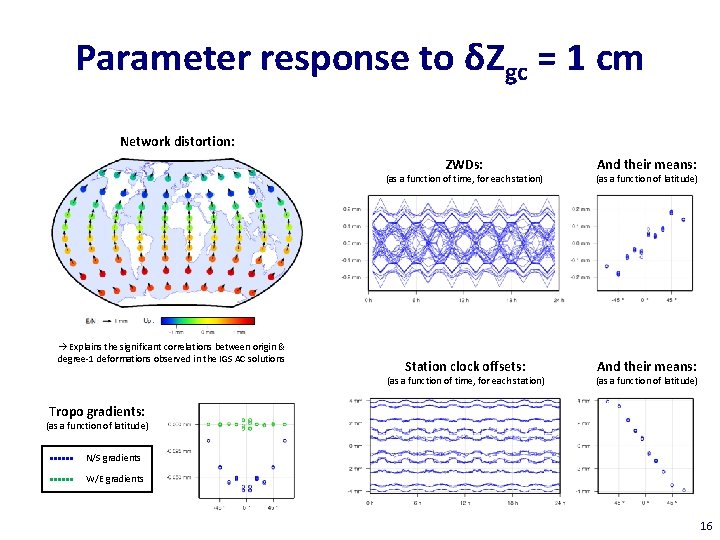
Parameter response to δZgc = 1 cm Network distortion: ZWDs: → Explains the significant correlations between origin & degree-1 deformations observed in the IGS AC solutions And their means: (as a function of time, for each station) (as a function of latitude) Station clock offsets: And their means: (as a function of time, for each station) (as a function of latitude) Tropo gradients: (as a function of latitude) N/S gradients W/E gradients 16

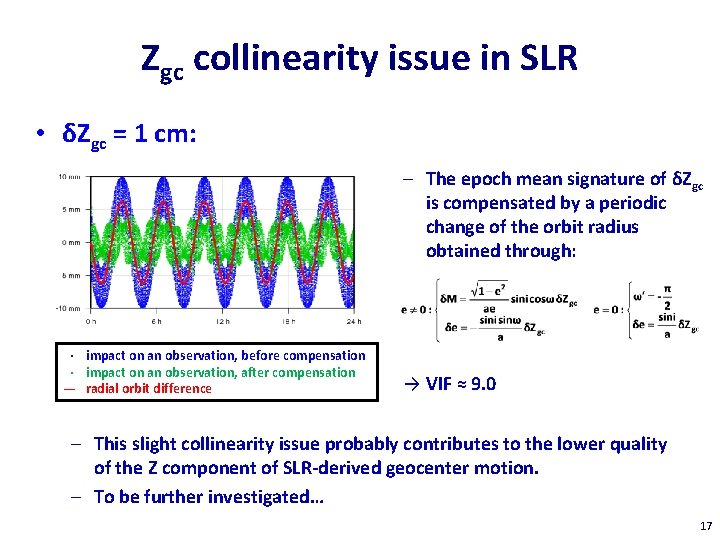
Zgc collinearity issue in SLR • δZgc = 1 cm: – The epoch mean signature of δZgc is compensated by a periodic change of the orbit radius obtained through: · impact on an observation, before compensation · impact on an observation, after compensation — radial orbit difference → VIF ≈ 9. 0 – This slight collinearity issue probably contributes to the lower quality of the Z component of SLR-derived geocenter motion. – To be further investigated… 17