Inscribed Angles Section 10 5 Essential Questions l

Inscribed Angles Section 10. 5

Essential Questions l 1. How to use inscribed angles to solve problems in geometry l 2. How to use inscribed angles to solve real-life problems

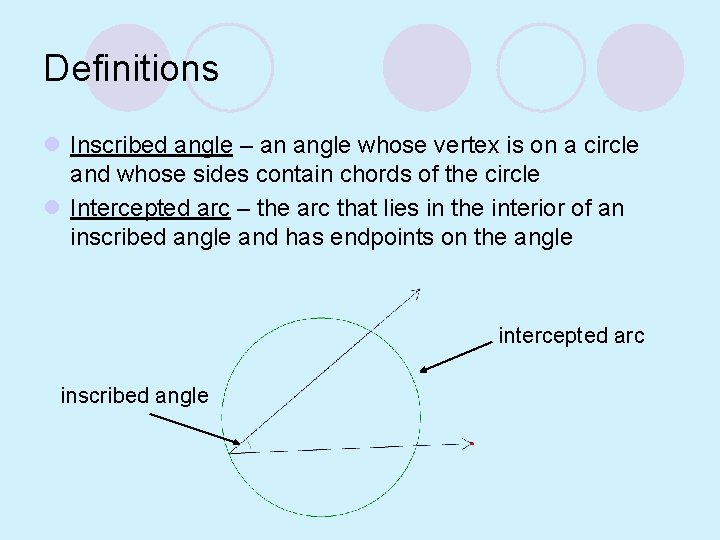
Definitions l Inscribed angle – an angle whose vertex is on a circle and whose sides contain chords of the circle l Intercepted arc – the arc that lies in the interior of an inscribed angle and has endpoints on the angle intercepted arc inscribed angle

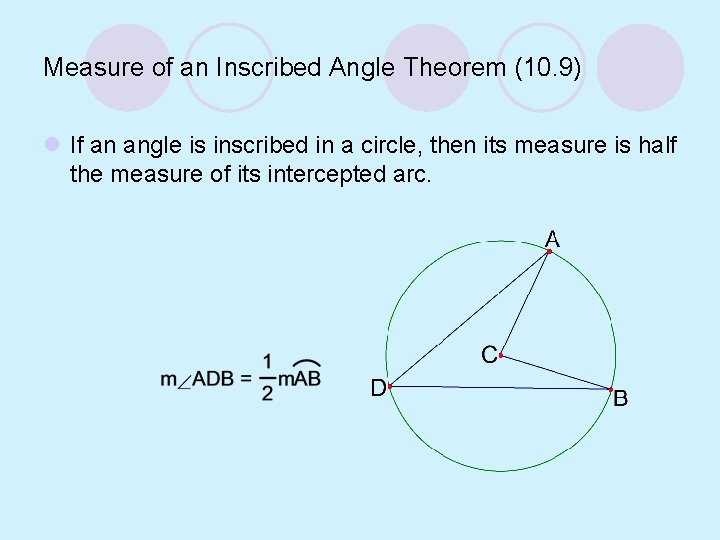
Measure of an Inscribed Angle Theorem (10. 9) l If an angle is inscribed in a circle, then its measure is half the measure of its intercepted arc.

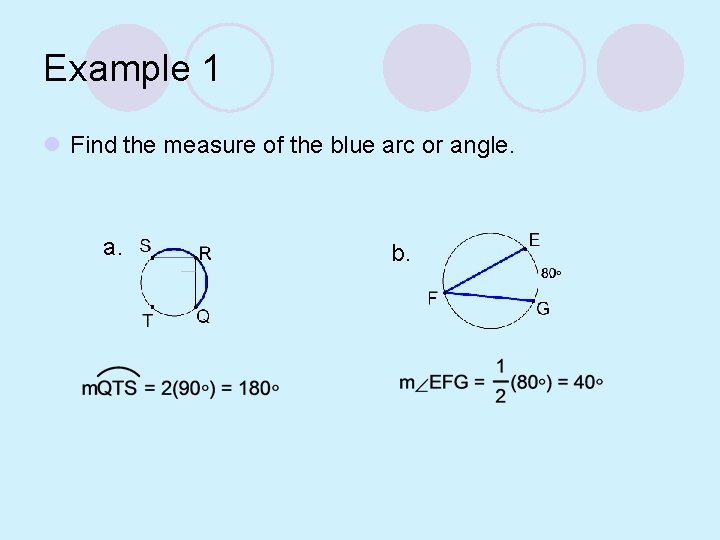
Example 1 l Find the measure of the blue arc or angle. a. b.

Congruent Inscribed Angles Theorem (10. 10) l If two inscribed angles of a circle intercept the same arc, then the angles are congruent.

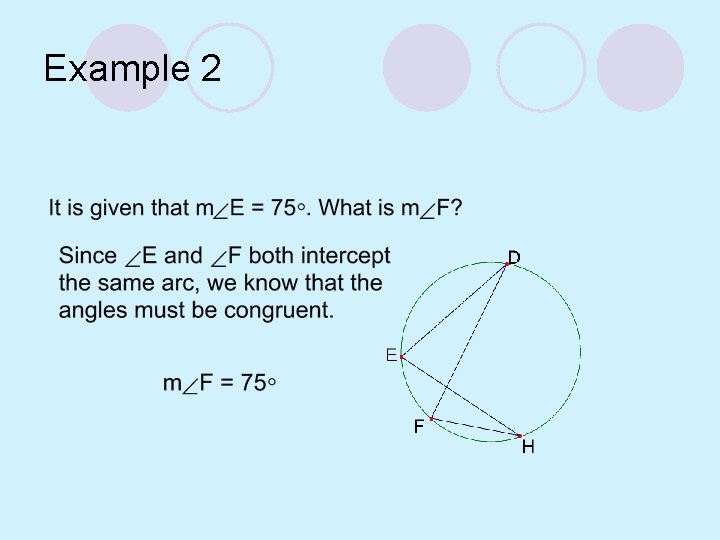
Example 2

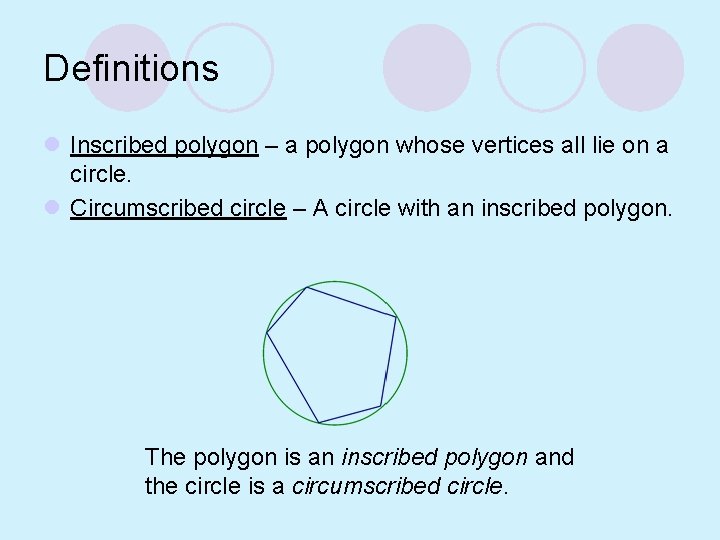
Definitions l Inscribed polygon – a polygon whose vertices all lie on a circle. l Circumscribed circle – A circle with an inscribed polygon. The polygon is an inscribed polygon and the circle is a circumscribed circle.

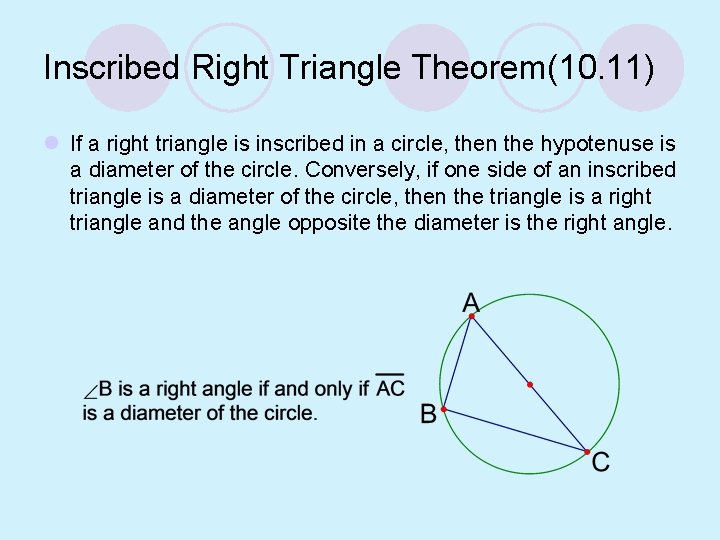
Inscribed Right Triangle Theorem(10. 11) l If a right triangle is inscribed in a circle, then the hypotenuse is a diameter of the circle. Conversely, if one side of an inscribed triangle is a diameter of the circle, then the triangle is a right triangle and the angle opposite the diameter is the right angle.

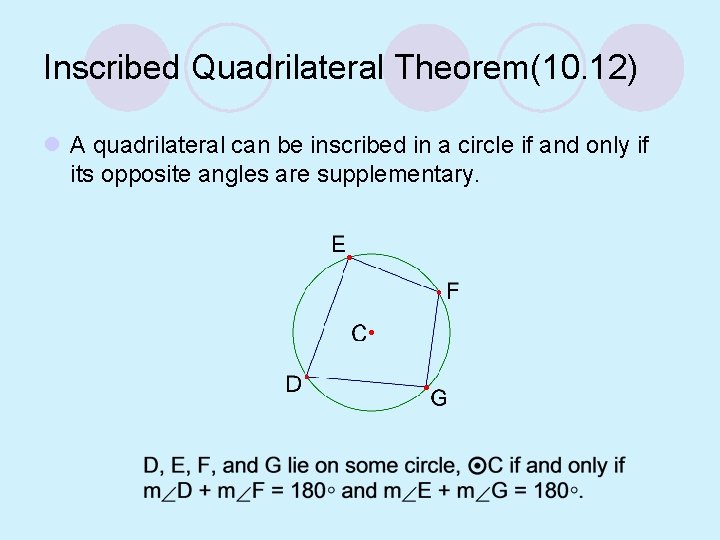
Inscribed Quadrilateral Theorem(10. 12) l A quadrilateral can be inscribed in a circle if and only if its opposite angles are supplementary.

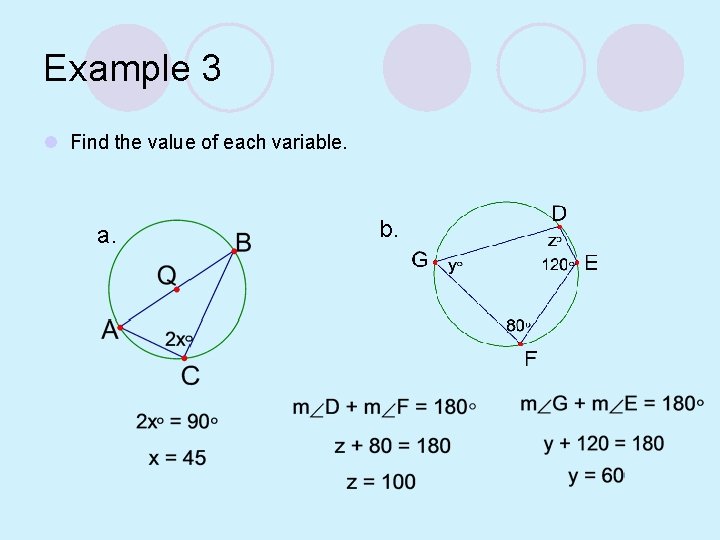
Example 3 l Find the value of each variable. a. b.

l Assignment: l P. 508/ 1 - 14 l HW: p. 508/ 15 - 33 all