Inscribed Angles Geometry 11 3 Using geometry tools

Inscribed Angles Geometry 11 -3

• Using geometry tools, or a calculator – Draw a large circle – Create a central angle and an inscribed angle that share the same points on the circle – Compare the measures Inscribed Angle Investigation

The measure of an angle inscribed in a circle is half the measure of its intercepted arc Inscribed Angle Theorem

Inscribed Angle Theorem

• Based on this last conjecture, what can do we know about an inscribed angle that intercepts a diameter of the circle? Inscribed Angle Investigation

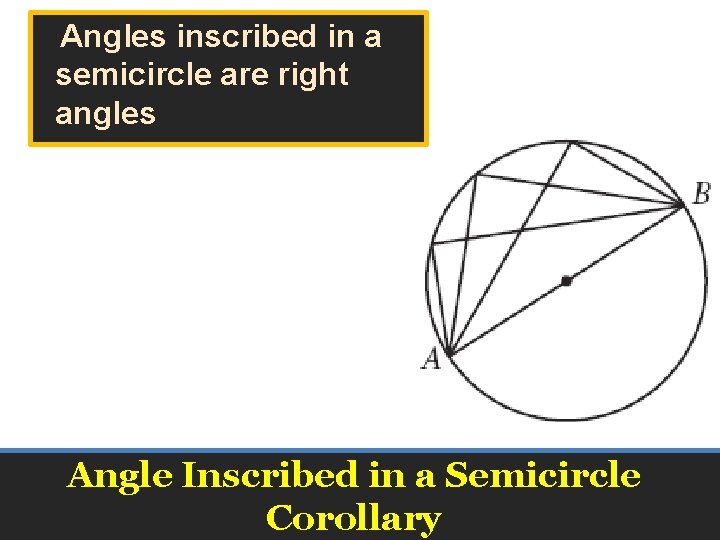
Angles inscribed in a semicircle are right angles Angle Inscribed in a Semicircle Corollary

• Using geometry tools, or a calculator – Create a second inscribed angle with a different vertex, but with the same intercepted arc as before – What can you conclude about the measures of the two angles? Inscribed Angle Investigation

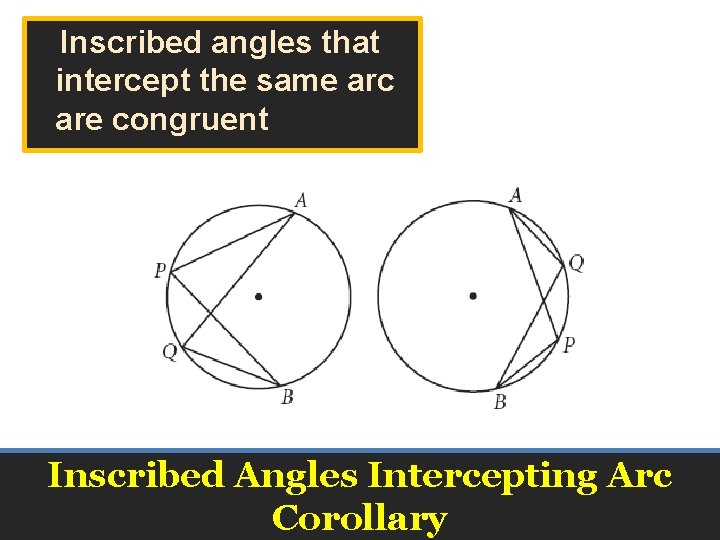
Inscribed angles that intercept the same arc are congruent Inscribed Angles Intercepting Arc Corollary

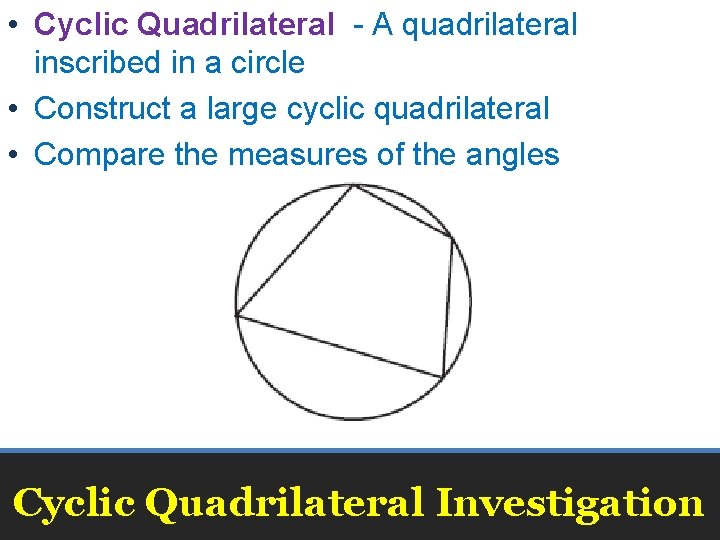
• Cyclic Quadrilateral - A quadrilateral inscribed in a circle • Construct a large cyclic quadrilateral • Compare the measures of the angles Cyclic Quadrilateral Investigation

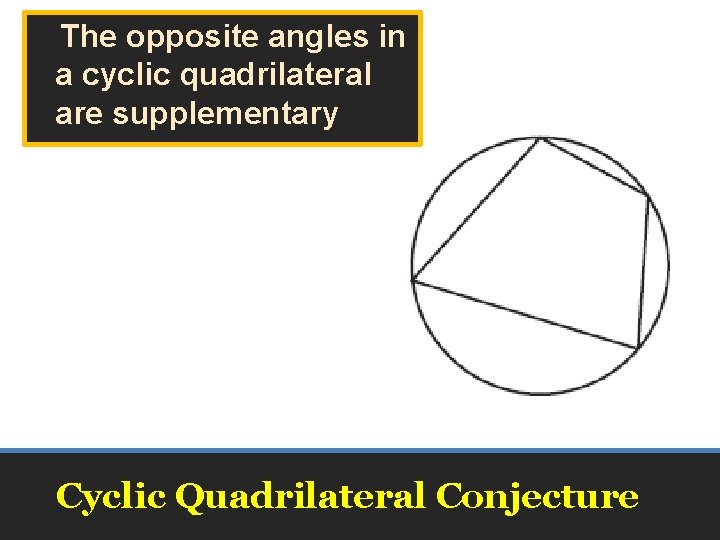
The opposite angles in a cyclic quadrilateral are supplementary Cyclic Quadrilateral Conjecture

Inscribed Angles

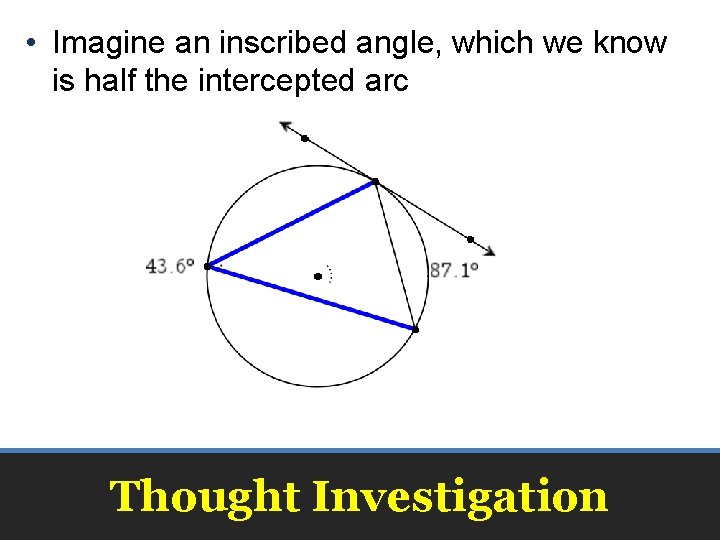
• Imagine an inscribed angle, which we know is half the intercepted arc Thought Investigation

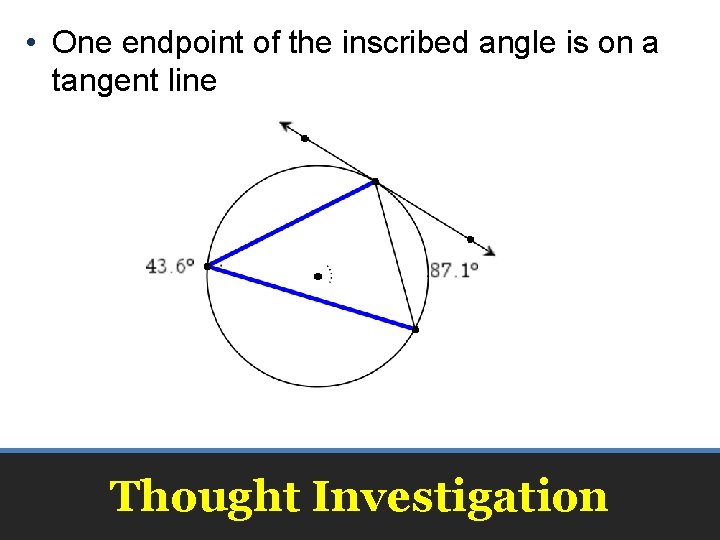
• One endpoint of the inscribed angle is on a tangent line Thought Investigation

• Move the vertex of the inscribed angle toward the tangent line, the angles value does not change, half the intercepted arc. Thought Investigation

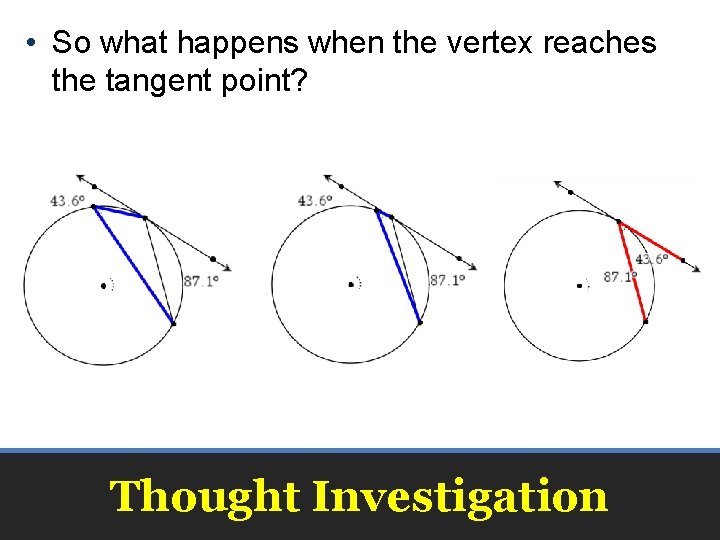
• So what happens when the vertex reaches the tangent point? Thought Investigation

Inscribed angles

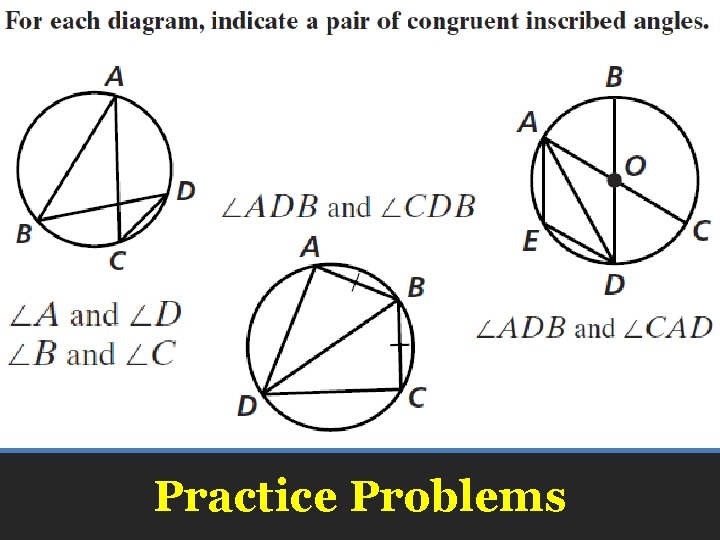
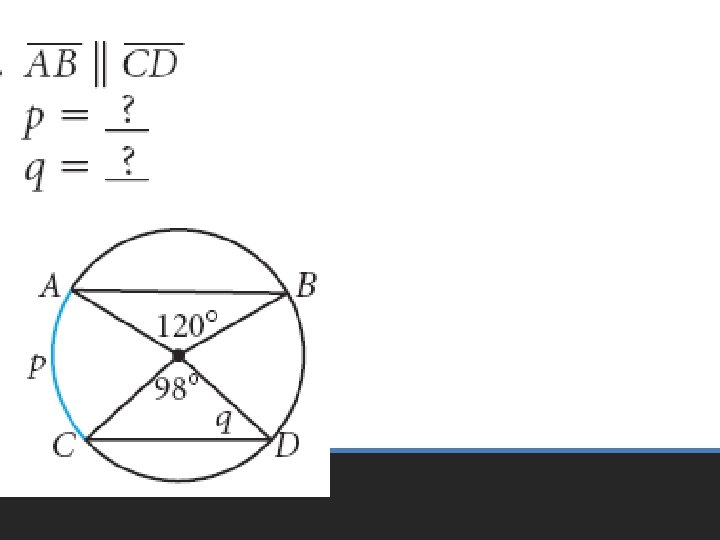
Practice Problems

Practice Problems

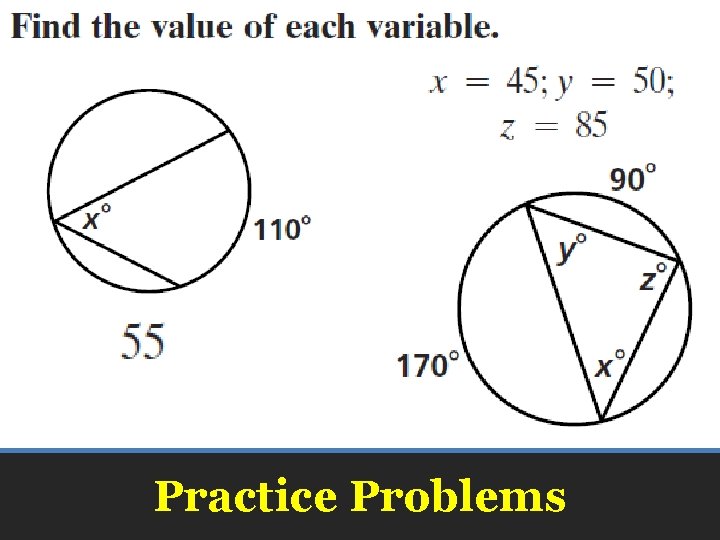
Practice Problems

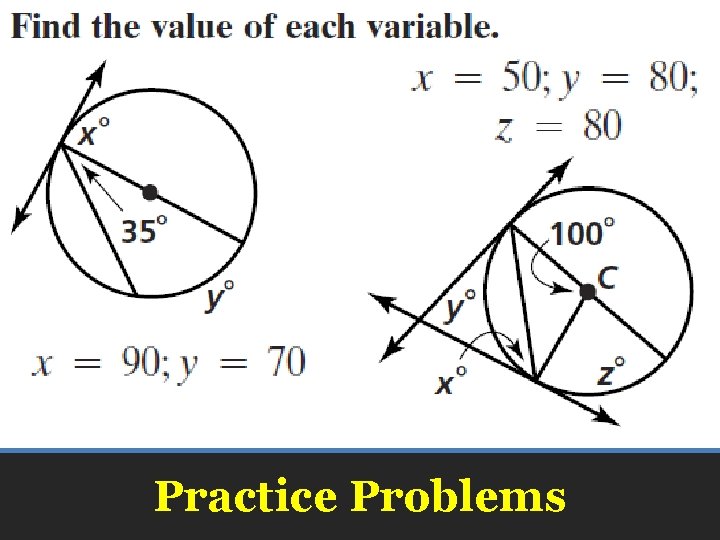
Practice Problems

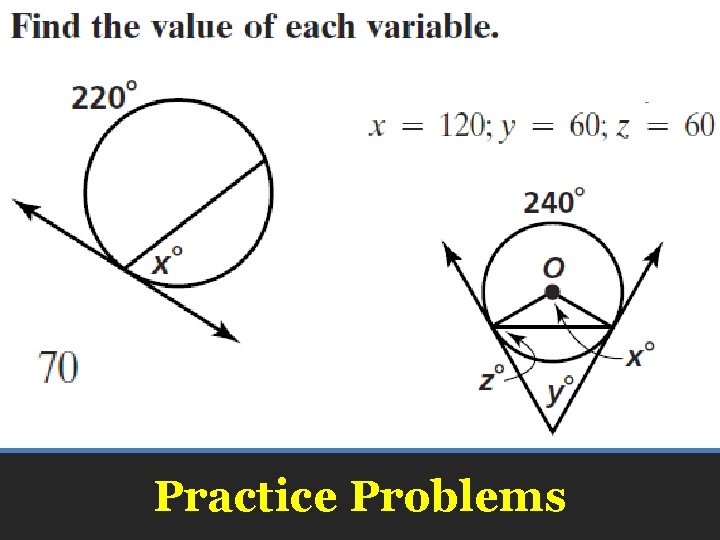
Practice Problems

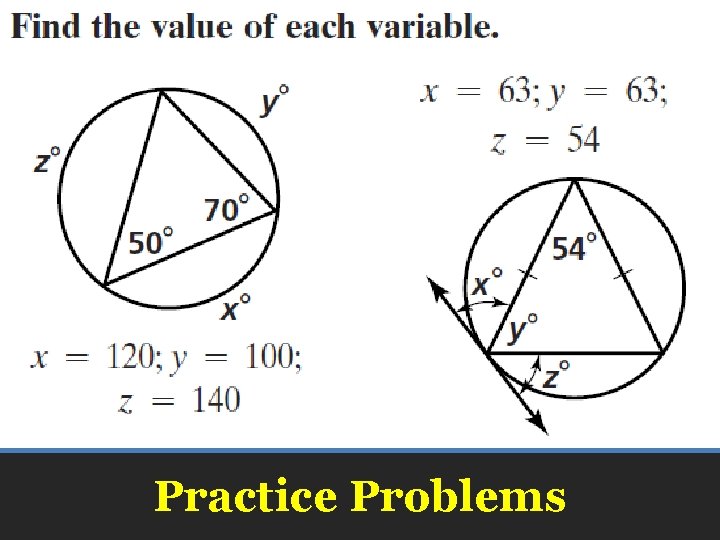
Practice Problems

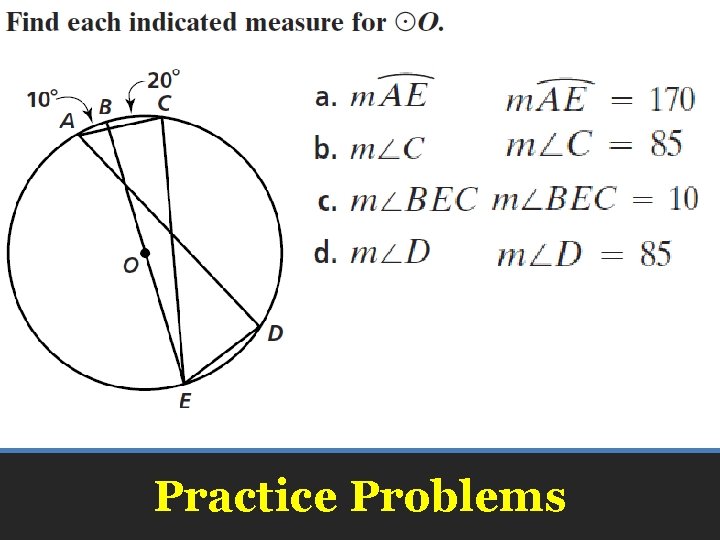
Practice Problems

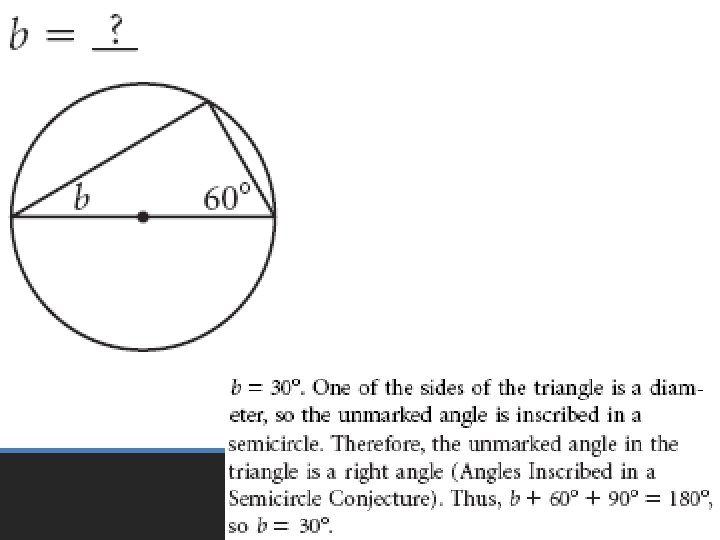
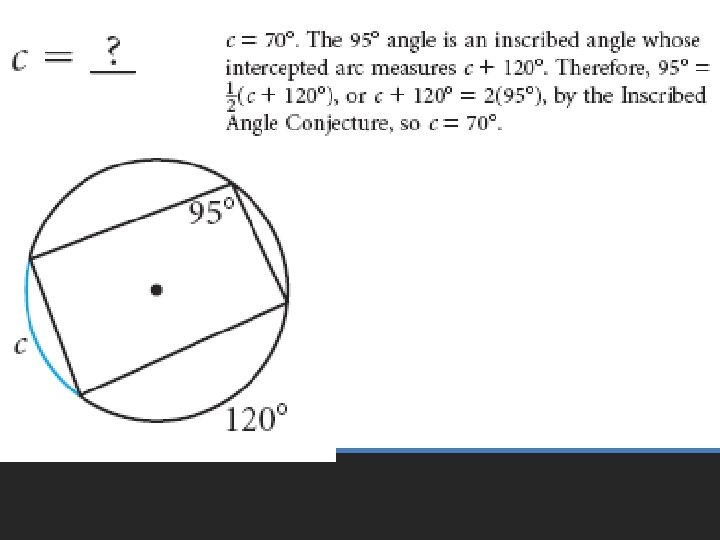
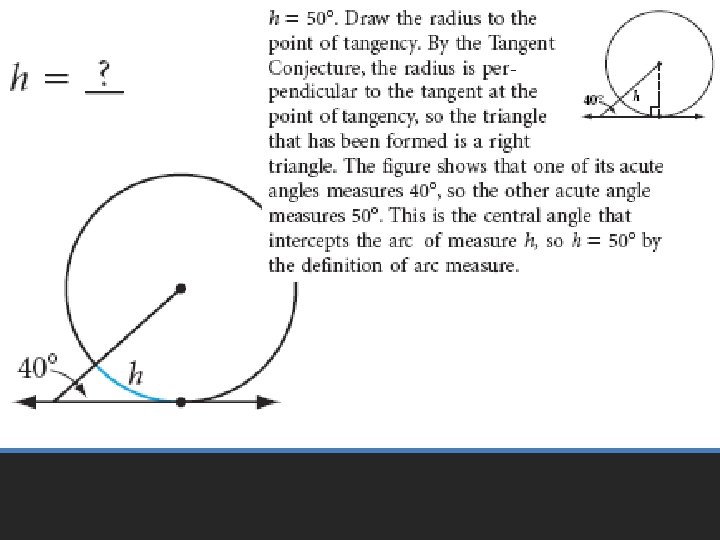
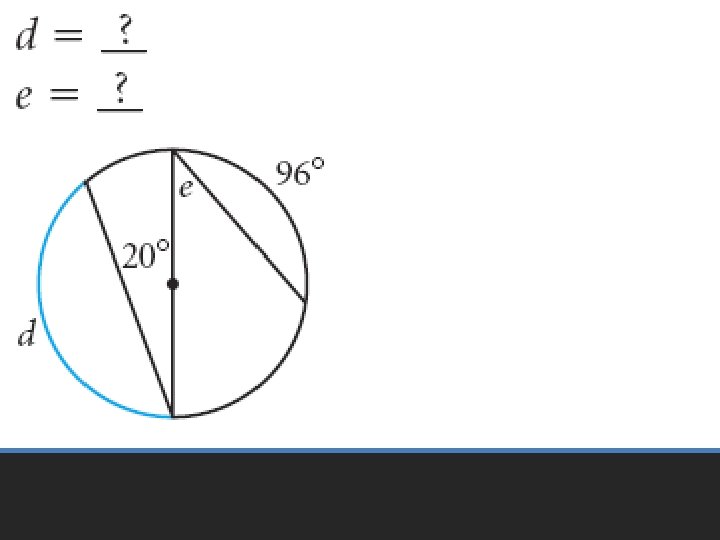
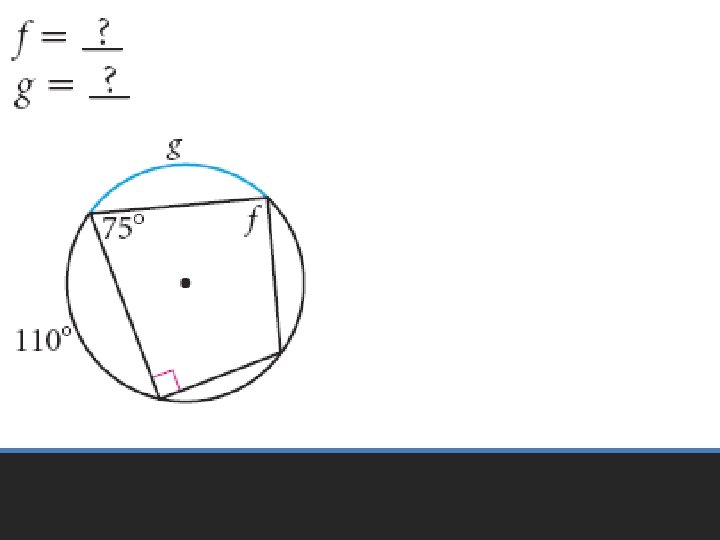
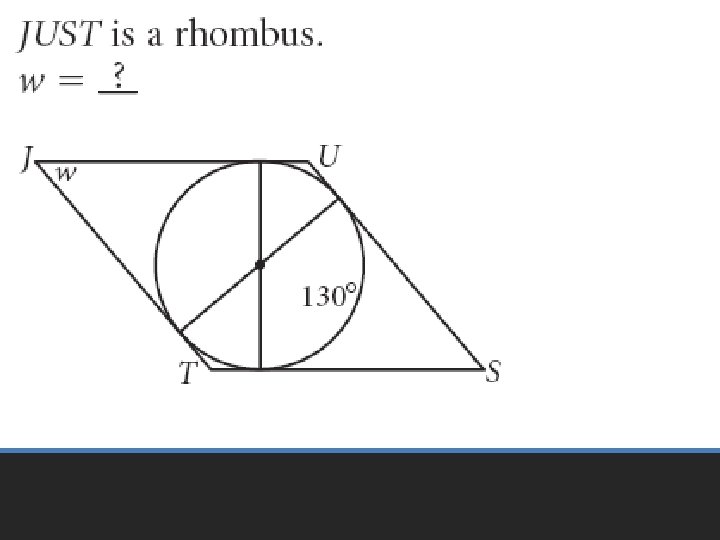
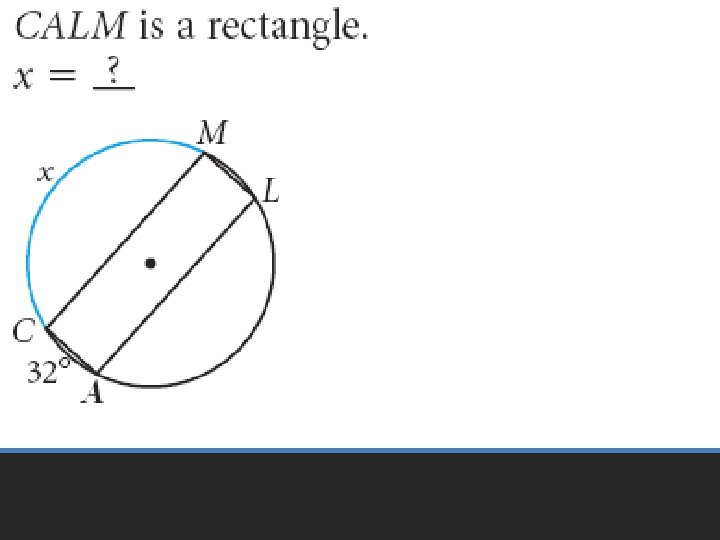
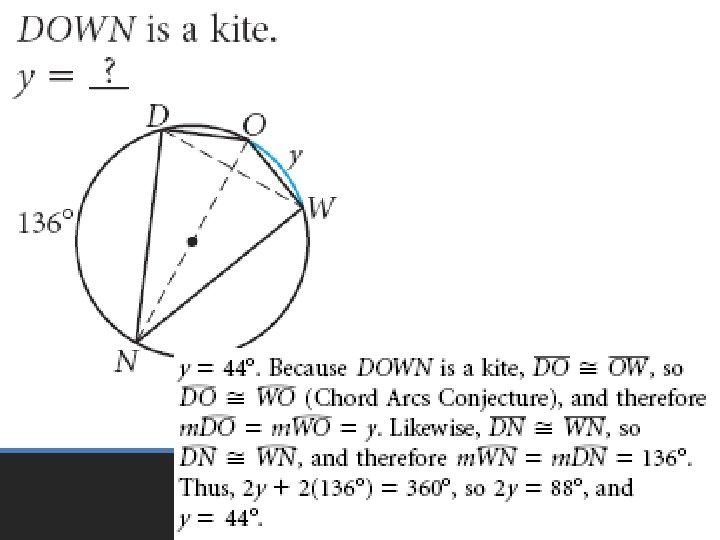
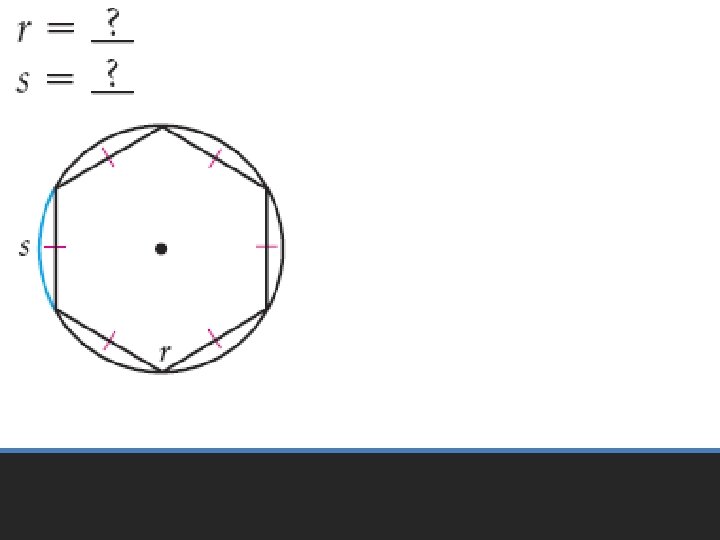
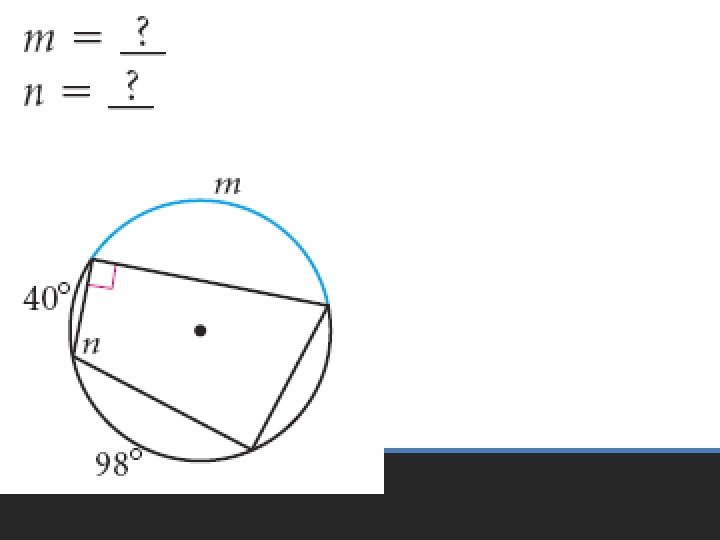
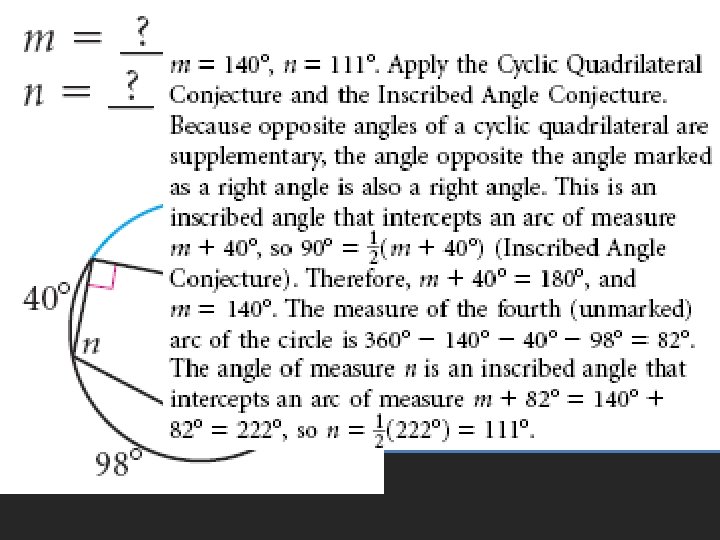
• Pages 601 – 605 • 6 – 24 even, 33 – 35, 51 – 53 Homework