Inscribed Angles Find measures of inscribed angles Find

Inscribed Angles • Find measures of inscribed angles • Find measures of angles of inscribed polygons. Three congruent central angles are pictured. What is the measure of each angle?

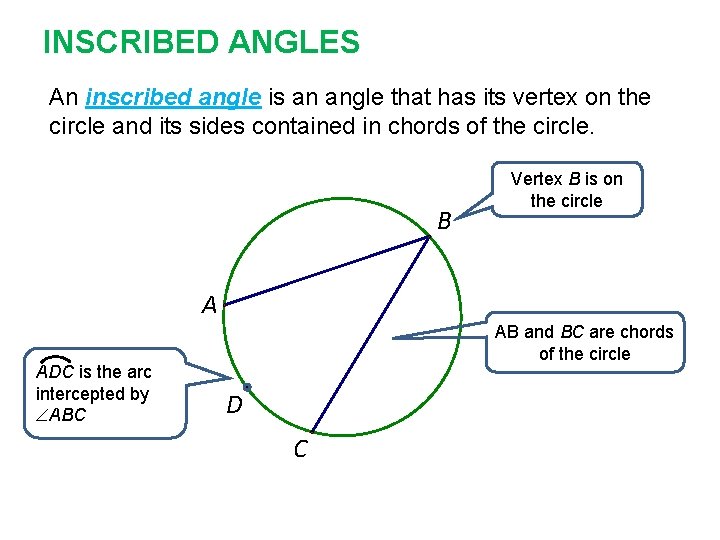
INSCRIBED ANGLES An inscribed angle is an angle that has its vertex on the circle and its sides contained in chords of the circle. B Vertex B is on the circle A ADC is the arc intercepted by ABC AB and BC are chords of the circle D C

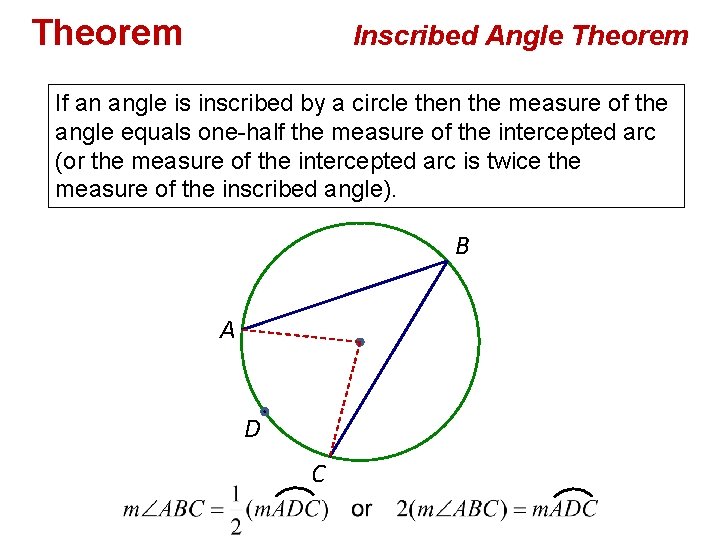
Theorem Inscribed Angle Theorem If an angle is inscribed by a circle then the measure of the angle equals one-half the measure of the intercepted arc (or the measure of the intercepted arc is twice the measure of the inscribed angle). B A D C

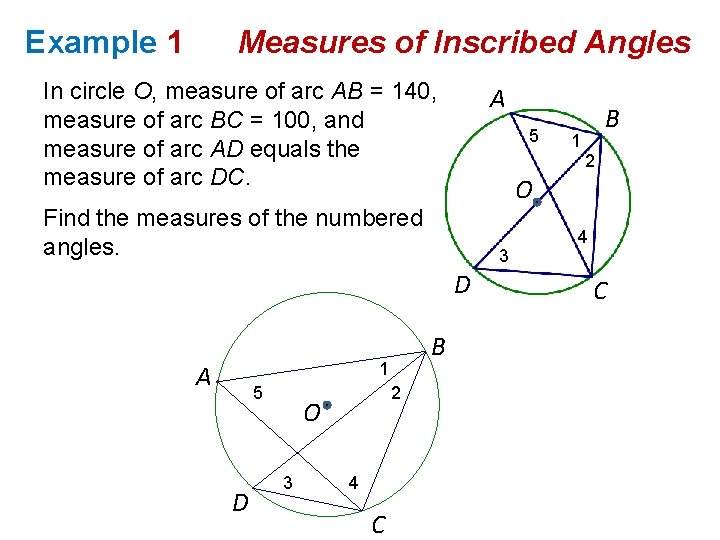
Example 1 Measures of Inscribed Angles In circle O, measure of arc AB = 140, measure of arc BC = 100, and measure of arc AD equals the measure of arc DC. A 5 3 D 1 A 5 D 2 O 3 4 C 2 O Find the measures of the numbered angles. B 1 B 4 C

Example 1 Measures of Inscribed Angles In circle O, measure of arc AB = 140, measure of arc BC = 100, and measure of arc AD equals the measure of arc DC. A 5 2 O Find the measures of the numbered angles. 3 D First find m. DC and m. AD 1 B 4 C

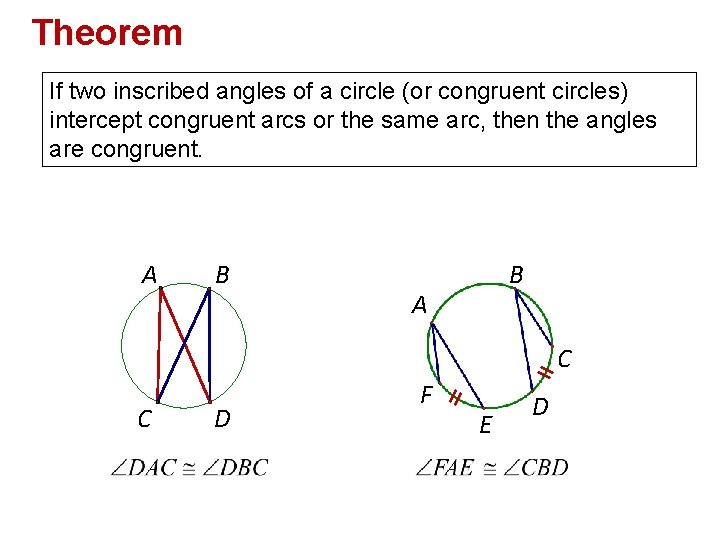
Theorem If two inscribed angles of a circle (or congruent circles) intercept congruent arcs or the same arc, then the angles are congruent. A B B A C C D F E D

Example 2 Inscribed Arcs and Probability

ANGLES OF INSCRIBED POLYGONS An inscribed triangle with a side that is a diameter is a special type of triangle.

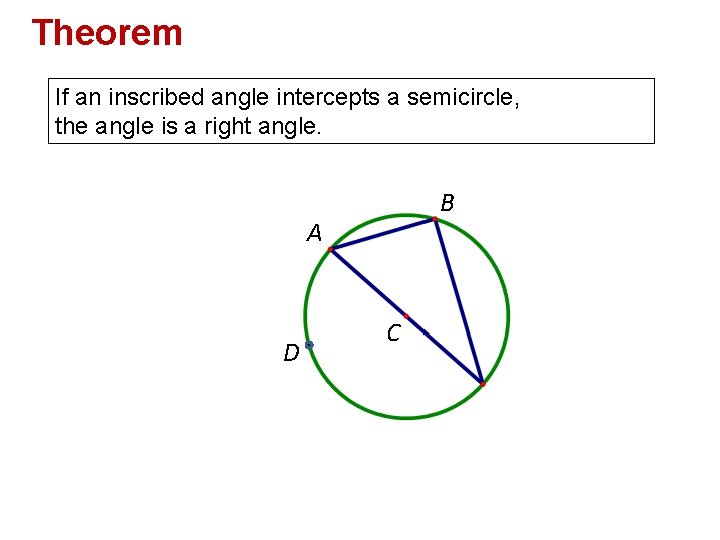
Theorem If an inscribed angle intercepts a semicircle, the angle is a right angle. B A D C

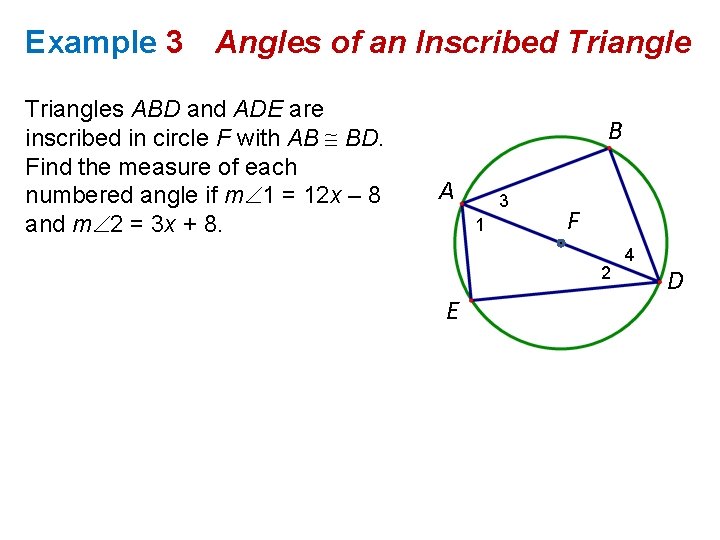
Example 3 Angles of an Inscribed Triangles ABD and ADE are inscribed in circle F with AB BD. Find the measure of each numbered angle if m 1 = 12 x – 8 and m 2 = 3 x + 8. B A 3 1 F 2 E 4 D

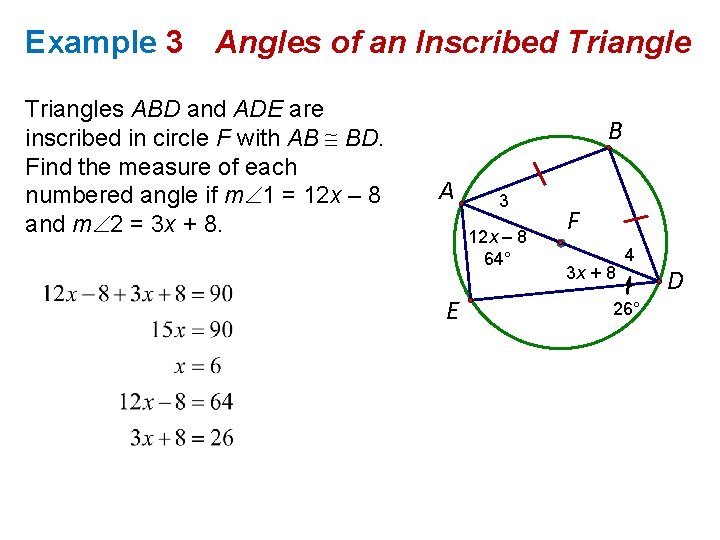
Example 3 Angles of an Inscribed Triangles ABD and ADE are inscribed in circle F with AB BD. Find the measure of each numbered angle if m 1 = 12 x – 8 and m 2 = 3 x + 8. B A 3 12 x – 8 64° E F 3 x + 8 4 26° D