Input Output Domain Range 1 Relation a set

  • Slides: 11
Download presentation
Input / Output & Domain / Range 1

Input / Output & Domain / Range 1

Relation- a set of ordered pairs Ex: {(-3, 1), (0, -2), (3, − 2)}

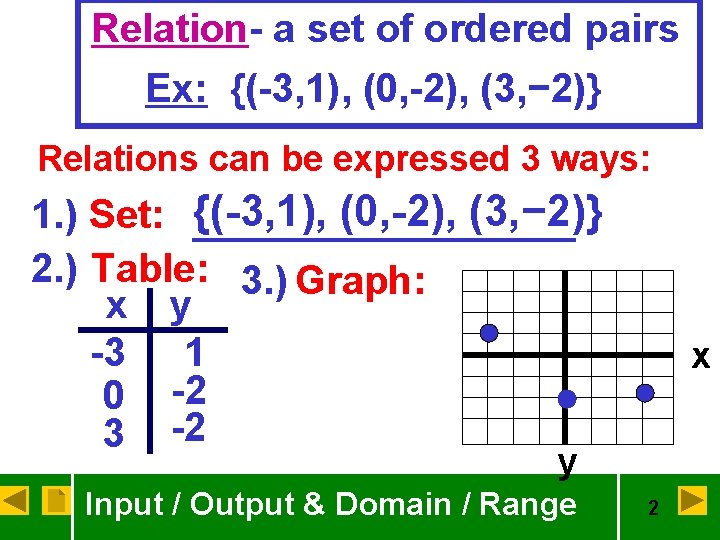
Relation- a set of ordered pairs Ex: {(-3, 1), (0, -2), (3, − 2)} Relations can be expressed 3 ways: 1. ) Set: {(-3, 1), (0, -2), (3, − 2)} 2. ) Table: 3. ) Graph: x y -3 1 0 -2 3 -2 x y Input / Output & Domain / Range 2

Relation- a set of ordered pairs Ex: {(-3, 1), (0, -2), (3, − 2)}

Relation- a set of ordered pairs Ex: {(-3, 1), (0, -2), (3, − 2)} Domain- the set of the first coordinate of each ordered pair. Domain = {-3, 0, 3} Range- the set of the second coordinate of each ordered pair. Range = {1, -2} Notice how the -2 is not repeated! Input / Output & Domain / Range 3

Try This: Write the Domain and Range of the following relation: {(1, 3), (5,

Try This: Write the Domain and Range of the following relation: {(1, 3), (5, -5), (-4, 0), (2, -3), (-5, -4)} Domain = {1, 5, -4, 2, -5} Range = {3, -5, 0, -3, -4} Input / Output & Domain / Range 4

Function - A relation in which each coordinate in the Domain is paired with

Function - A relation in which each coordinate in the Domain is paired with exactly one coordinate in the Range. Are these functions? A. {(-1, -1), (0, 0), (4, -4), (5, -5)} Yes B. {(1, 4), (0, 0), (1, -2), (2, -4)} No Input / Output & Domain / Range 5

You can also think of the Domain as the Input (or x value) and

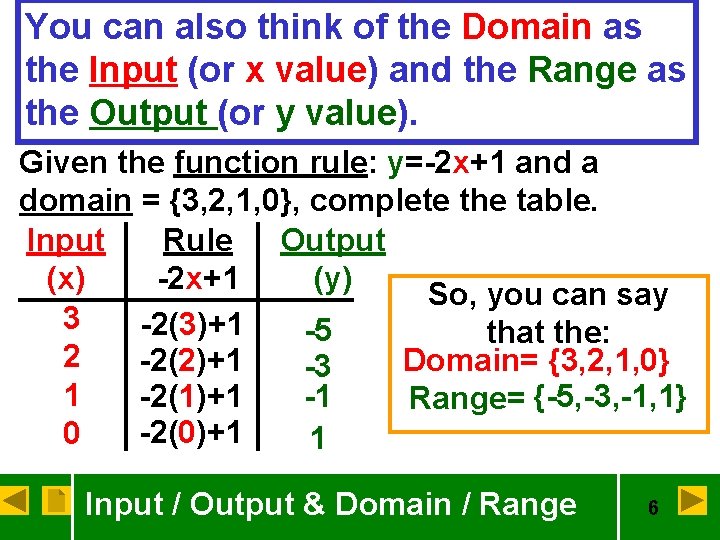
You can also think of the Domain as the Input (or x value) and the Range as the Output (or y value). Given the function rule: y=-2 x+1 and a domain = {3, 2, 1, 0}, complete the table. Input Rule Output (x) -2 x+1 (y) So, you can say 3 -2(3)+1 -5 that the: 2 -2(2)+1 Domain= {3, 2, 1, 0} -3 1 -2(1)+1 -1 Range= {-5, -3, -1, 1} -2(0)+1 0 1 Input / Output & Domain / Range 6

You can graph the function by using the Domain and the Range to write

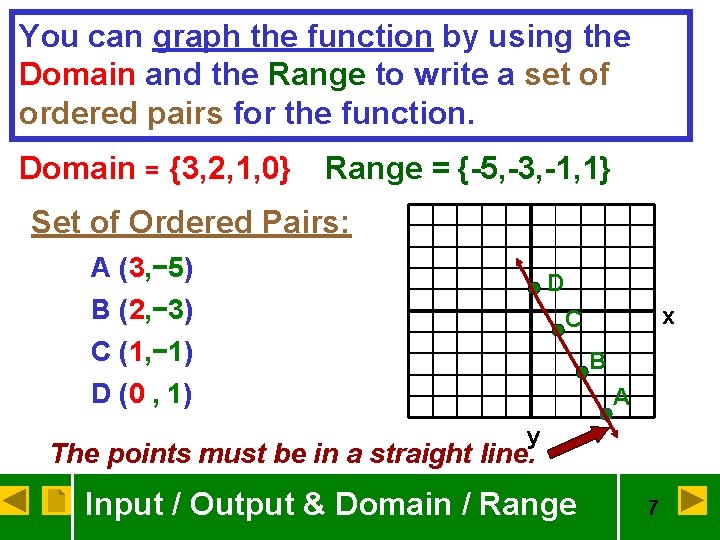
You can graph the function by using the Domain and the Range to write a set of ordered pairs for the function. Domain = {3, 2, 1, 0} Range = {-5, -3, -1, 1} Set of Ordered Pairs: A (3, − 5) D B (2, − 3) C (1, − 1) D (0 , 1) x C B A y The points must be in a straight line. Input / Output & Domain / Range 7

Try This: Given the function rule y=½x+1 and a domain = {4, 2, −

Try This: Given the function rule y=½x+1 and a domain = {4, 2, − 4} complete the table. First input the x-value (domain) into the function to find the output y-value (range). INPUT (x) 4 2 -2 -4 ½x+1 ½(4)+1 ½(2)+1 ½(-4)+1 OUTPUT (y) Now using the 3 table, give the: 2 Domain= {4, 2, -2, − 4} Range= {3, 2, 0, − 1} 0 − 1 Input / Output & Domain / Range 8

Next: Write a set of ordered pairs for the function and graph the function

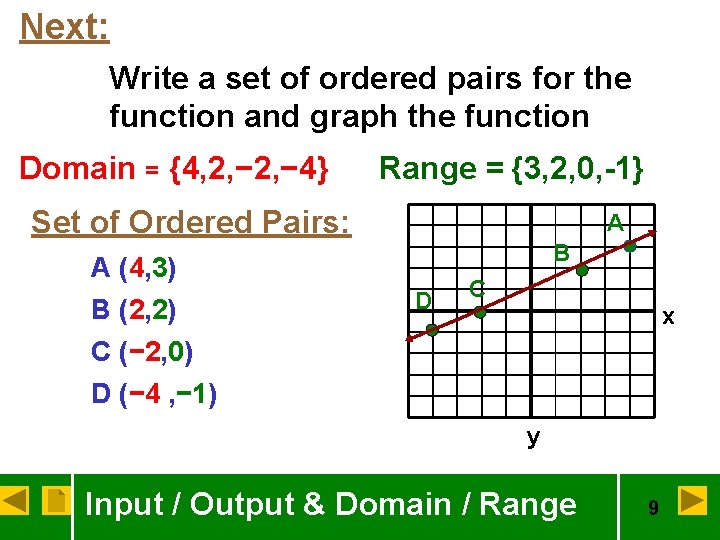
Next: Write a set of ordered pairs for the function and graph the function Domain = {4, 2, − 4} Range = {3, 2, 0, -1} Set of Ordered Pairs: A B A (4, 3) B (2, 2) C (− 2, 0) D (− 4 , − 1) D C x y Input / Output & Domain / Range 9

Try This: Given the function rule y=x− 3 and a domain = {0, 1,

Try This: Given the function rule y=x− 3 and a domain = {0, 1, 2, 3}, complete the table: First input the x-value (domain) into the function to find the output y-value (range). INPUT Rule (x) x− 3 0 (0)− 3 (1)− 3 1 2 (2) − 3 (3)− 3 3 OUTPUT (y) Now using the table, give the: − 3 Domain= {0, 1, 2, 3} − 2 Range= {-3, -2, − 1, 0} − 1 0 Input / Output & Domain / Range 10

Next: Write a set of ordered pairs for the function and graph the function

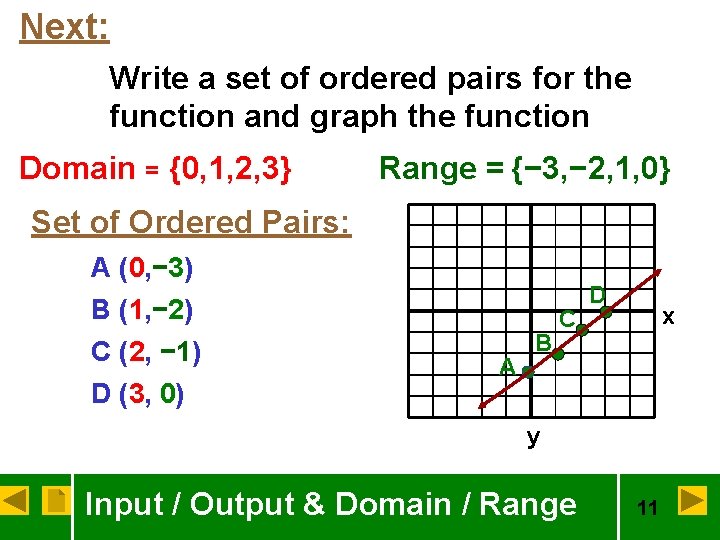
Next: Write a set of ordered pairs for the function and graph the function Domain = {0, 1, 2, 3} Range = {− 3, − 2, 1, 0} Set of Ordered Pairs: A (0, − 3) B (1, − 2) C (2, − 1) D (3, 0) A B C D x y Input / Output & Domain / Range 11