Initial beam studies using symplectic 2 D space

Initial beam studies using symplectic 2 D space charge with open BCs Stephen Webb, David Bruhwiler, Nathan Cook, Jon Edelen, Chris Hall, Ilya Pogorelov Radia. Soft, LLC. , Boulder, CO swebb@radiasoft. net 4 th Space Charge Workshop 4 November 2019 Boulder, Colorado USA – www. radiasoft. net

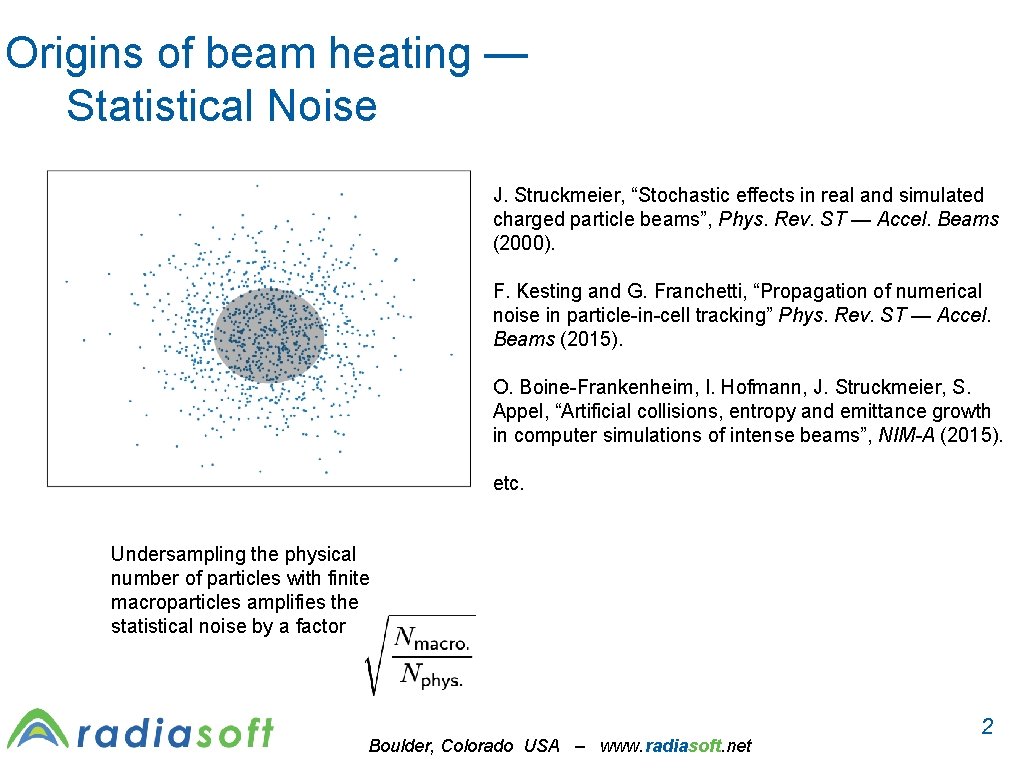
Origins of beam heating — Statistical Noise J. Struckmeier, “Stochastic effects in real and simulated charged particle beams”, Phys. Rev. ST — Accel. Beams (2000). F. Kesting and G. Franchetti, “Propagation of numerical noise in particle-in-cell tracking” Phys. Rev. ST — Accel. Beams (2015). O. Boine-Frankenheim, I. Hofmann, J. Struckmeier, S. Appel, “Artificial collisions, entropy and emittance growth in computer simulations of intense beams”, NIM-A (2015). etc. Undersampling the physical number of particles with finite macroparticles amplifies the statistical noise by a factor Boulder, Colorado USA – www. radiasoft. net 2

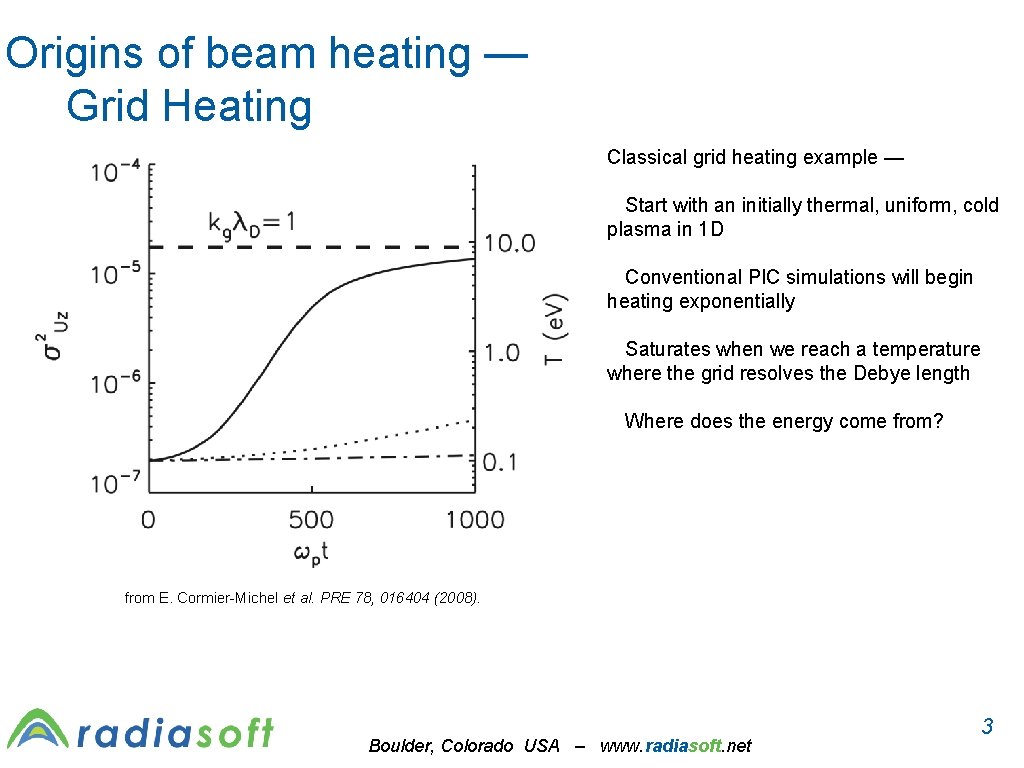
Origins of beam heating — Grid Heating Classical grid heating example — Start with an initially thermal, uniform, cold plasma in 1 D Conventional PIC simulations will begin heating exponentially Saturates when we reach a temperature where the grid resolves the Debye length Where does the energy come from? from E. Cormier-Michel et al. PRE 78, 016404 (2008). Boulder, Colorado USA – www. radiasoft. net 3

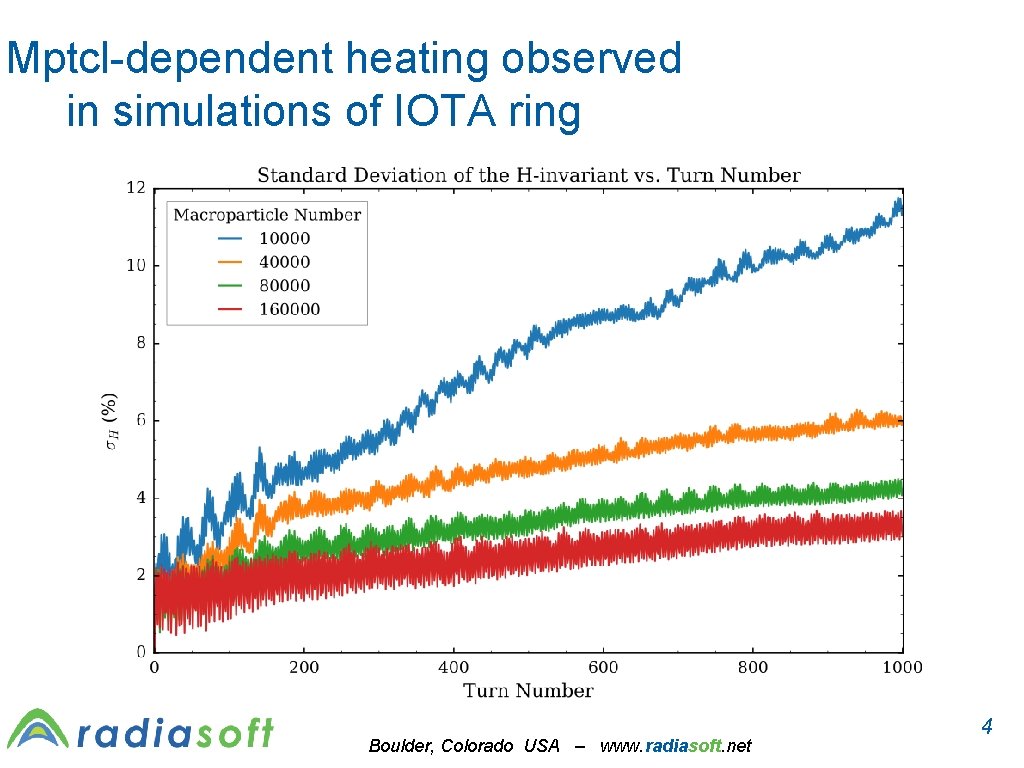
Mptcl-dependent heating observed in simulations of IOTA ring Boulder, Colorado USA – www. radiasoft. net 4

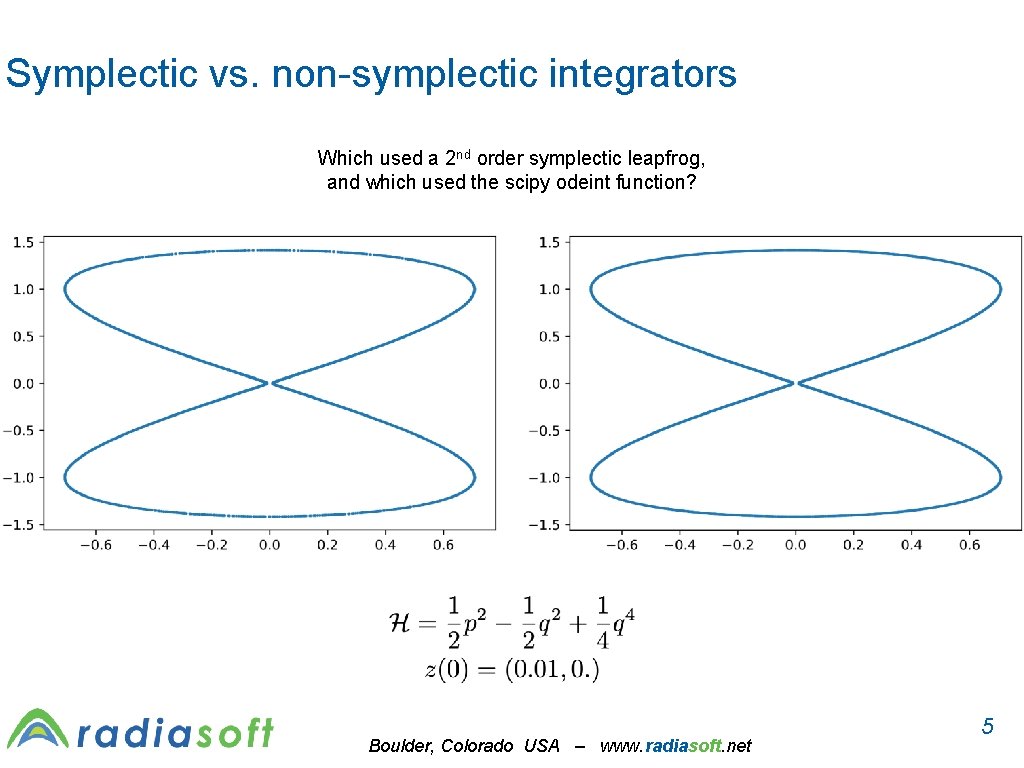
Symplectic vs. non-symplectic integrators Which used a 2 nd order symplectic leapfrog, and which used the scipy odeint function? Boulder, Colorado USA – www. radiasoft. net 5

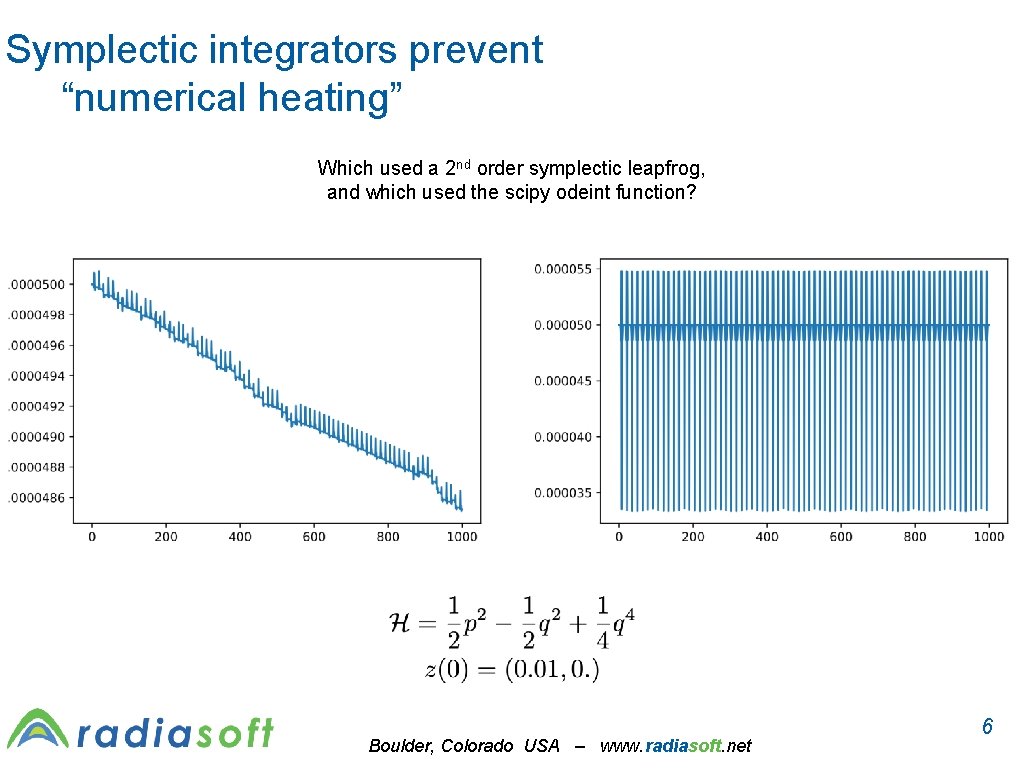
Symplectic integrators prevent “numerical heating” Which used a 2 nd order symplectic leapfrog, and which used the scipy odeint function? Boulder, Colorado USA – www. radiasoft. net 6

Symplectic integrators preserve a pseudo-Hamiltonian Physical Hamiltonian Numerical Hamiltonian • computable from BCH series • converges to physical Hamiltonian as dt → 0 • subject to Hamiltonian perturbation theory S. P. Auerbach and A. Friedman, “Long-time behaviour of numerically computed orbits: Small and intermediate timestep analysis of onedimensional systems”, J. Comp. Phys. 93, 1 (1991). Boulder, Colorado USA – www. radiasoft. net 7

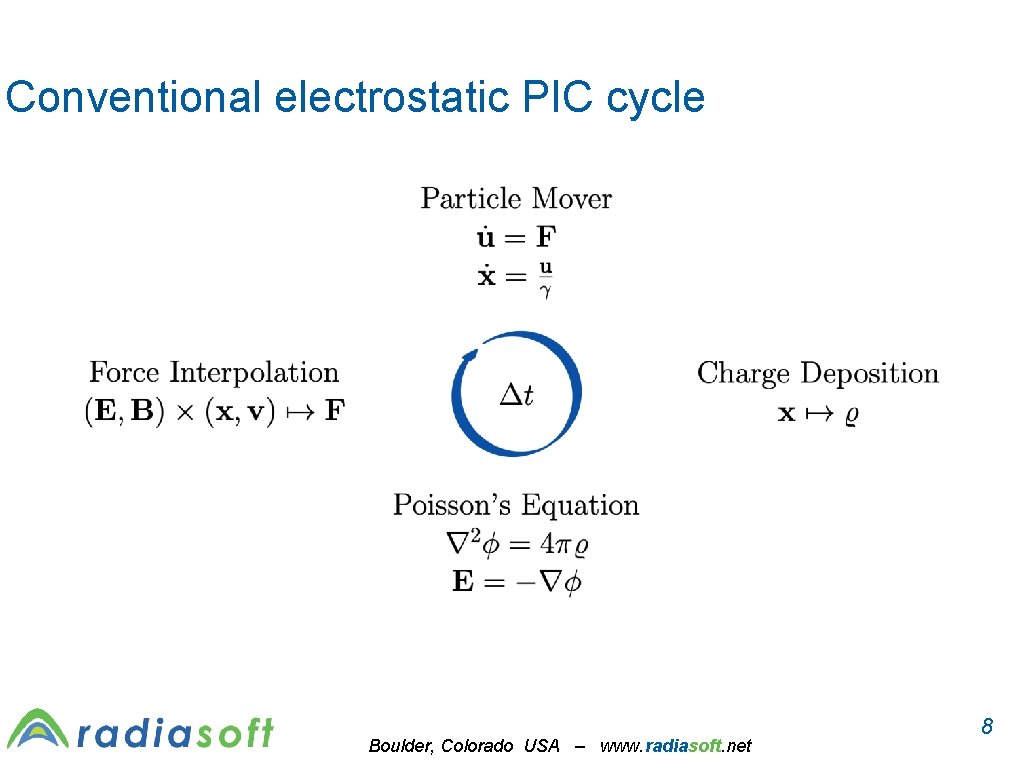
Conventional electrostatic PIC cycle Boulder, Colorado USA – www. radiasoft. net 8

Self-consistent symplectic algorithms start with the action integral Procedure for self-consistent symplectic algorithms 1. Discretize fields using some basis functions (Fourier-Bessel modes, splines, Legendre polynomials, etc. ) 2. Discretize phase space into macroparticles 3. Evaluate the volumetric integrals 4. a. Discretize the action in time* b. Convert to a Hamiltonian F. E. Low, “A Lagrangian formulation of the Boltzmann-Vlasov equation for plasmas”, Proc. Royal Soc. A (1958). *J. E. Marsden and M. West, “Discrete mechanics and variational integrators”, Acta Numerica (2001). Boulder, Colorado USA – www. radiasoft. net 9

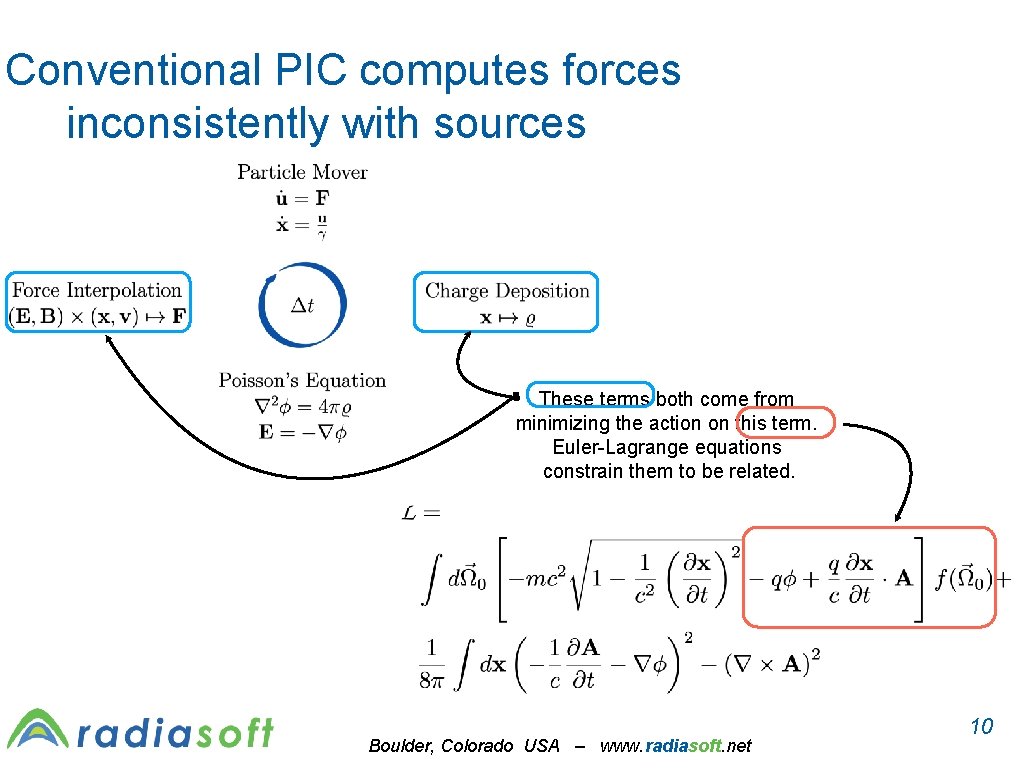
Conventional PIC computes forces inconsistently with sources These terms both come from minimizing the action on this term. Euler-Lagrange equations constrain them to be related. Boulder, Colorado USA – www. radiasoft. net 10

A series of approximations leads to a relativistic, electrostatic algorithm Change to s-dependent tracking; particles cannot “turn around”, so cannot work near the source. Self-consistent forces only come from longitudinal vector potential and scalar potential — no radiation. Change to co-moving coordinates; assumes small velocity spread. “small” transverse dynamics; neglects fringe fields. Boulder, Colorado USA – www. radiasoft. net 11

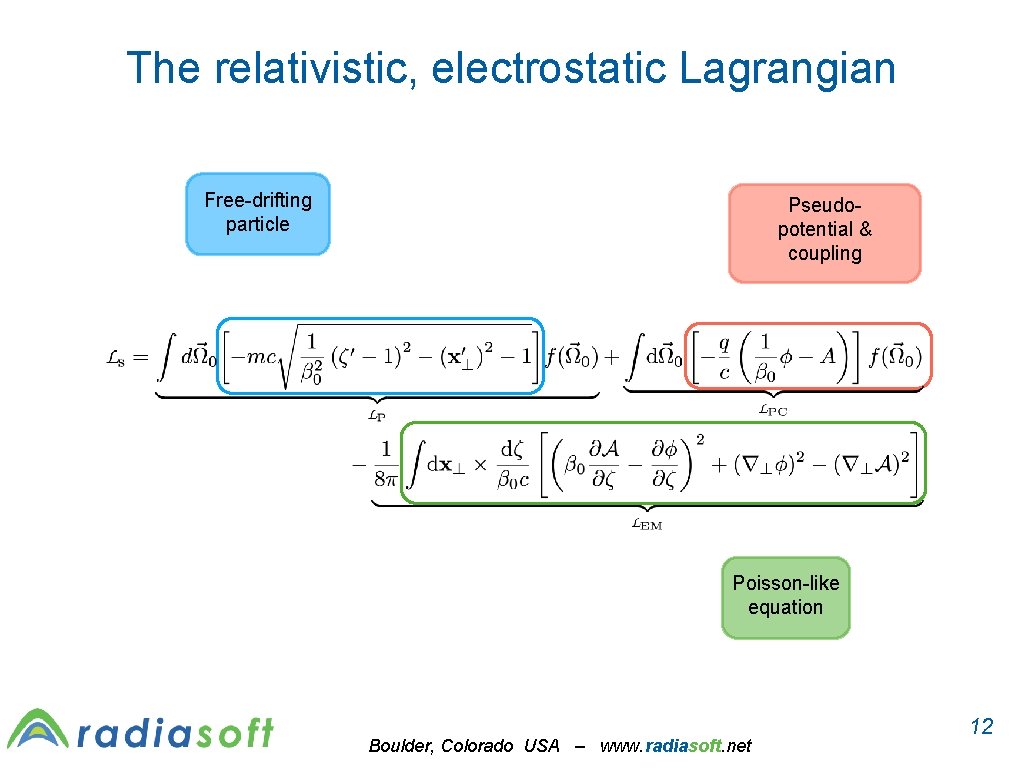
The relativistic, electrostatic Lagrangian Free-drifting particle Pseudopotential & coupling Poisson-like equation Boulder, Colorado USA – www. radiasoft. net 12

Represent the fields as Fourier modes No s-derivative of the fields → no field canonical momentum; → degenerate Lagrangian — i. e. “no Hamiltonian”; → can get away with it here, but an issue to be aware of for e. g. magnetostatics Boulder, Colorado USA – www. radiasoft. net 13

Particle Discretization Define macroparticles as floating tracers in configuration space Changes the particle-coupling term Defines the “dressed potentials”, the macroparticles interact through their shape with the fields Boulder, Colorado USA – www. radiasoft. net 14

Hamiltonian + Poisson Equation Free-drifting particle External Potentials Self-consistent dressed pseudopotential Poisson-like pseudopotential equation Self-consistent dressed pseudopotential Boulder, Colorado USA – www. radiasoft. net 15

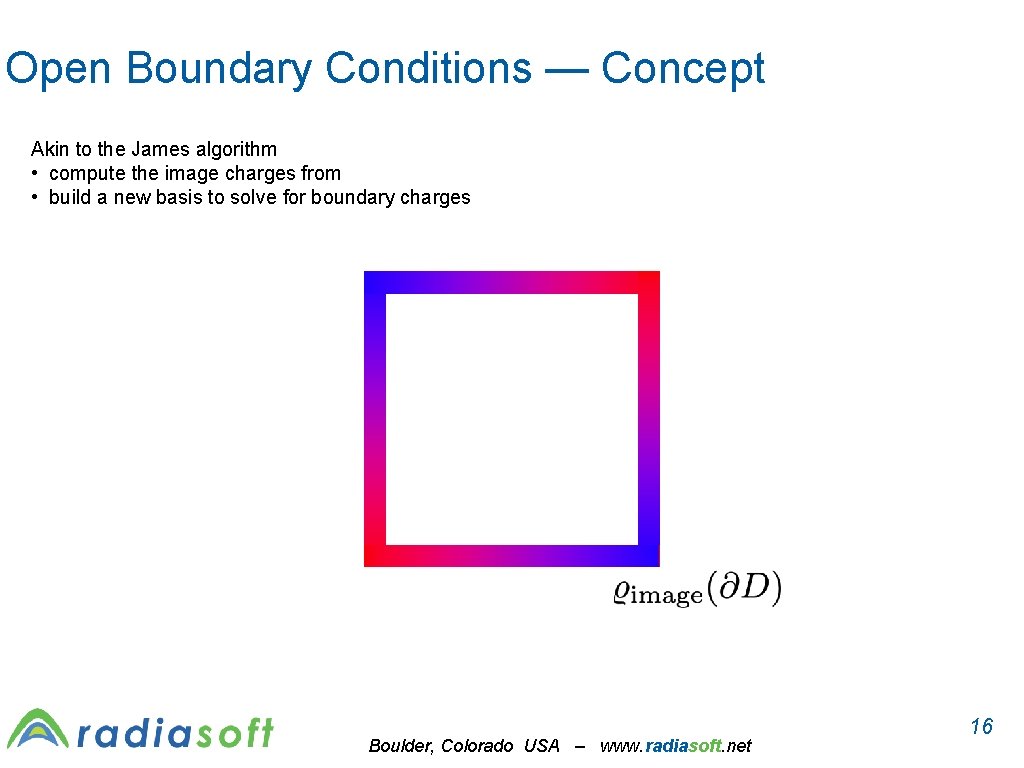
Open Boundary Conditions — Concept Akin to the James algorithm • compute the image charges from • build a new basis to solve for boundary charges Boulder, Colorado USA – www. radiasoft. net 16

Open Boundary Conditions — Implementation Sol’n w/ conducting boundaries Defines the Dirichlet boundary sol’n. Fills in the potential from the boundary Boulder, Colorado USA – www. radiasoft. net 17

Examples of the Algorithm Two working implementations: • rsrespic, dev library — https: //github. com/radiasoft/rsrespic • Synergia, dev branch — email me for a copy Boulder, Colorado USA – www. radiasoft. net 18

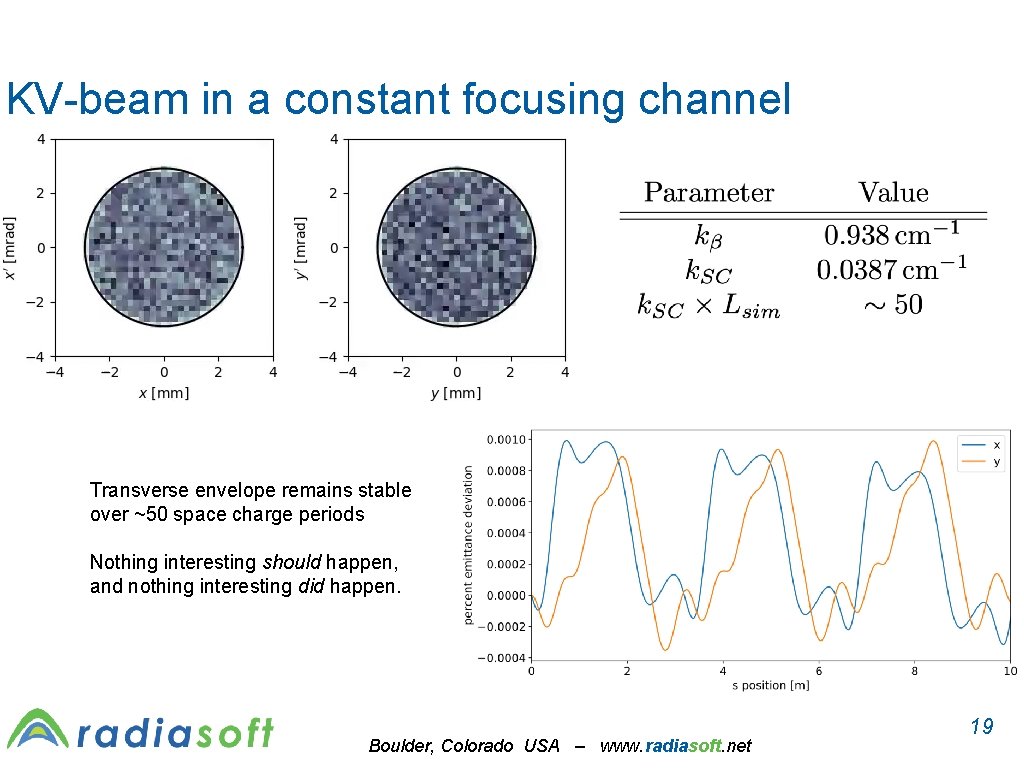
KV-beam in a constant focusing channel Transverse envelope remains stable over ~50 space charge periods Nothing interesting should happen, and nothing interesting did happen. Boulder, Colorado USA – www. radiasoft. net 19

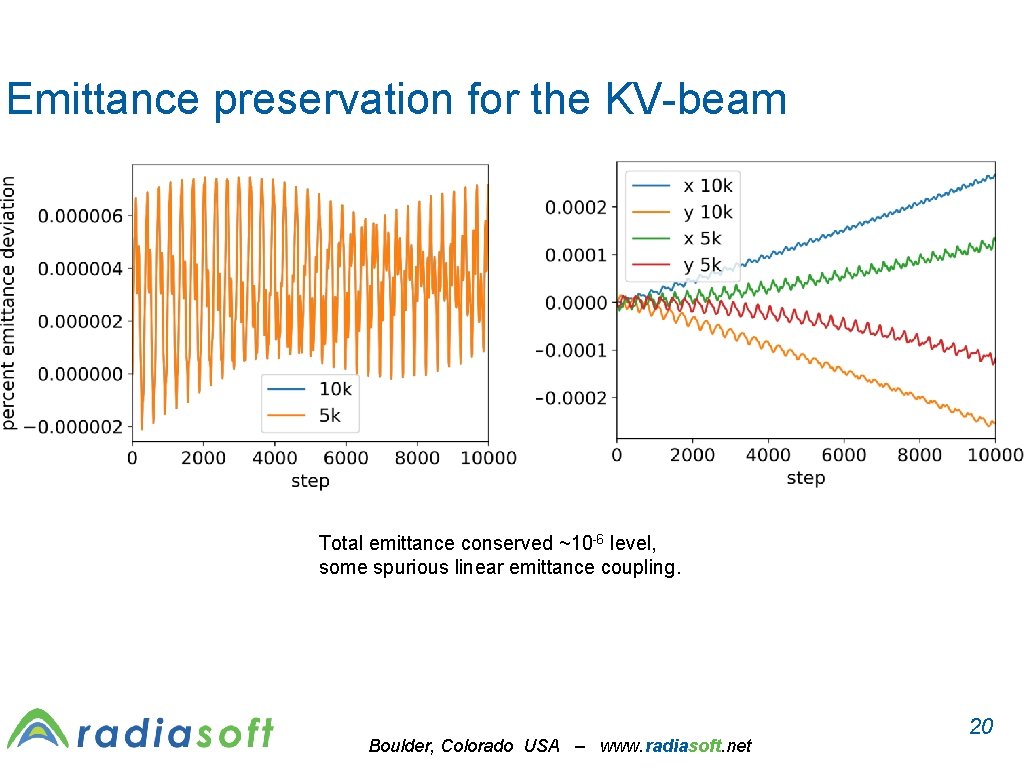
Emittance preservation for the KV-beam Total emittance conserved ~10 -6 level, some spurious linear emittance coupling. Boulder, Colorado USA – www. radiasoft. net 20

Octupole nonlinear resonance in a FODO channel • • Tune the FODO tune to just above the 1/4 -integer Increase current to put tune depression on the resonance Linear space charge depresses the tune across the 1/4 -integer Octupolar space charge forces drive resonant islands Boulder, Colorado USA – www. radiasoft. net 21

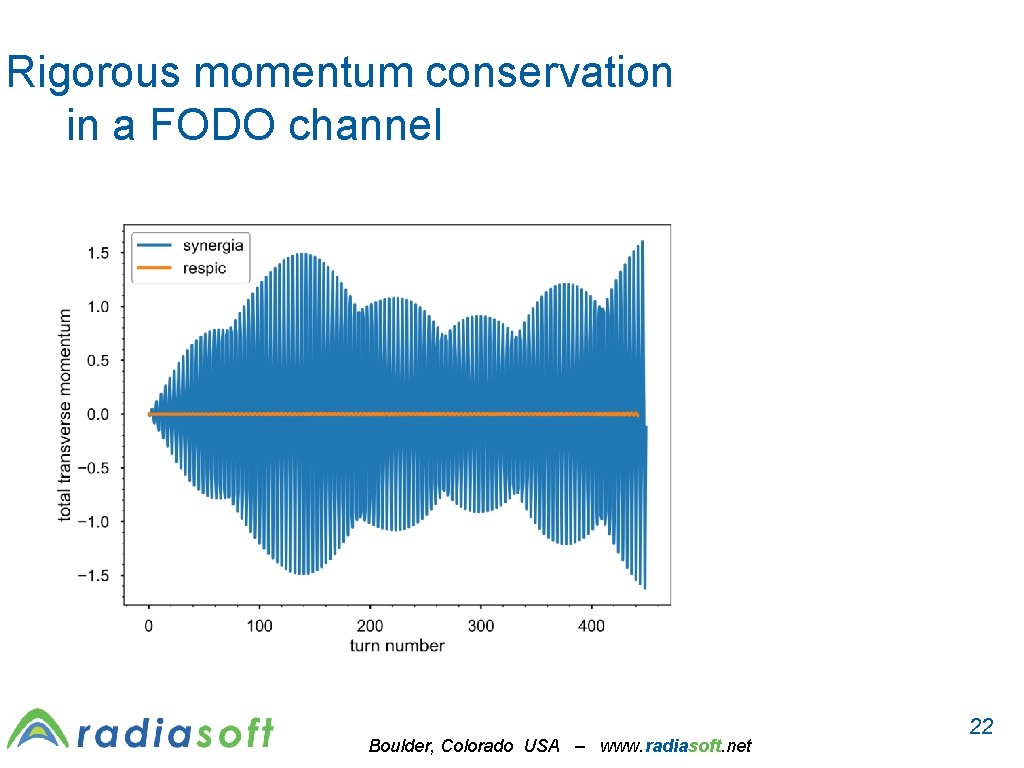
Rigorous momentum conservation in a FODO channel Boulder, Colorado USA – www. radiasoft. net 22

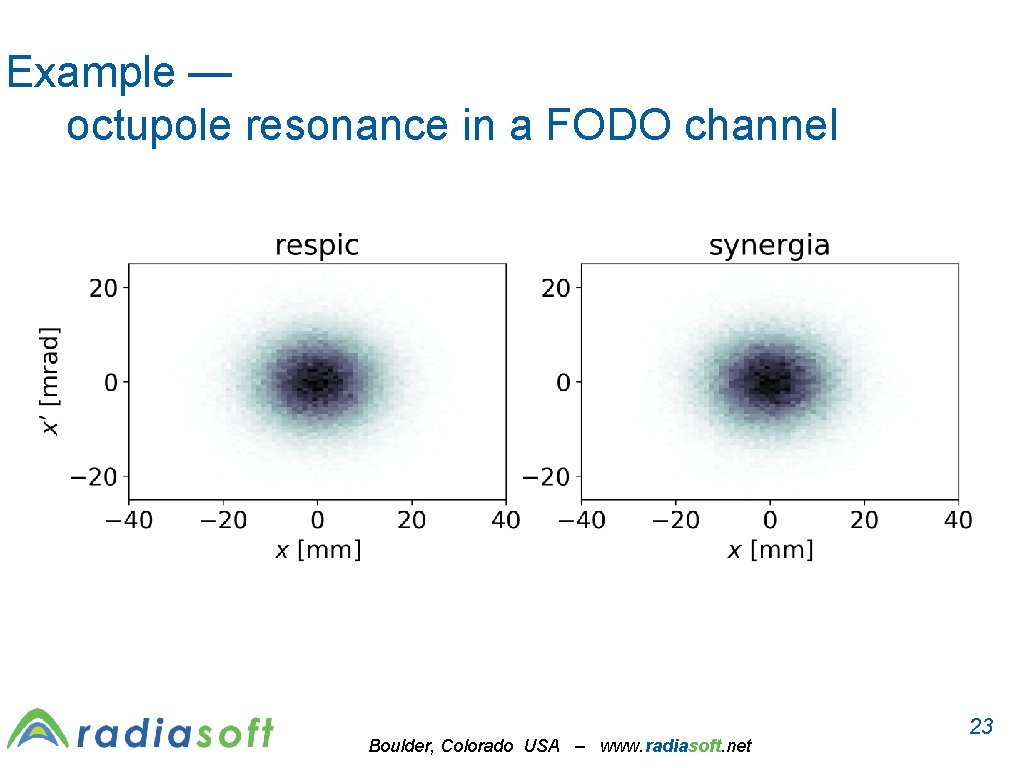
Example — octupole resonance in a FODO channel Boulder, Colorado USA – www. radiasoft. net 23

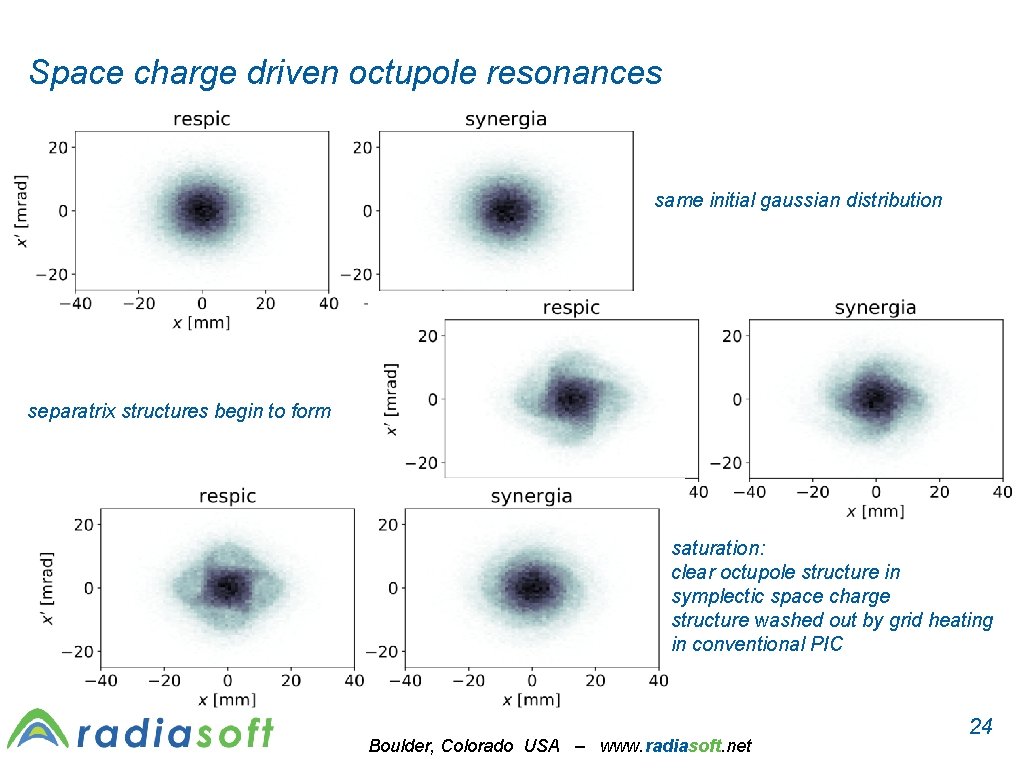
Space charge driven octupole resonances same initial gaussian distribution separatrix structures begin to form saturation: clear octupole structure in symplectic space charge structure washed out by grid heating in conventional PIC Boulder, Colorado USA – www. radiasoft. net 24

Symplectic Space Charge, Status & Future Work Problems Symplectic Space Charge solves: • Grid heating — existence of a conserved pseudo -Hamiltonian means no spurious energy growth Problems Symplectic PIC does not solve: • Particle noise* — still need many macro particles Three challenges to spectral symplectic space charge solvers: • Global Deposition — poor scaling with number of modes, • Global Deposition — parallel performance tied to All. Reduce() • Force Interpolation — scales with number of modes Gridded Poisson solvers suffer none of these, but do have the same challenges as a conventional Poisson solver — load balancing, memory-nonlocal deposition… Particle shapes and how they affect noise — C. E. Mitchell and J. Qiang, “Analysis of Particle Noise in a Gridless Spectral Poisson Solver for Symplectic Multiparticle Tracking”, Proc. Of IPAC’ 19 WEPTS 079 (2019). Boulder, Colorado USA – www. radiasoft. net 25

Thank you This material is based upon work supported by the U. S. Department of Energy, Office of Science, Office of High Energy Physics, under Award Number DESC 0011340. Boulder, Colorado USA – www. radiasoft. net 26

Symplectic Space Charge, Status & Future Work Problems Symplectic Space Charge solves: • Grid heating — existence of a conserved pseudo -Hamiltonian means no spurious energy growth Problems Symplectic PIC does not solve: • Particle noise* — still need many macro particles Three challenges to spectral symplectic space charge solvers: • Global Deposition — poor scaling with number of modes, • Global Deposition — parallel performance tied to All. Reduce() • Force Interpolation — scales with number of modes Gridded Poisson solvers suffer none of these, but do have the same challenges as a conventional Poisson solver — load balancing, memory-nonlocal deposition… Particle shapes and how they affect noise — C. E. Mitchell and J. Qiang, “Analysis of Particle Noise in a Gridless Spectral Poisson Solver for Symplectic Multiparticle Tracking”, Proc. Of IPAC’ 19 WEPTS 079 (2019). Boulder, Colorado USA – www. radiasoft. net 27