InfraRed IR Spectroscopy or Vibrational spectroscopy Applied Chemistry

Infra-Red (IR) Spectroscopy or Vibrational spectroscopy Applied Chemistry Course: CHY 101

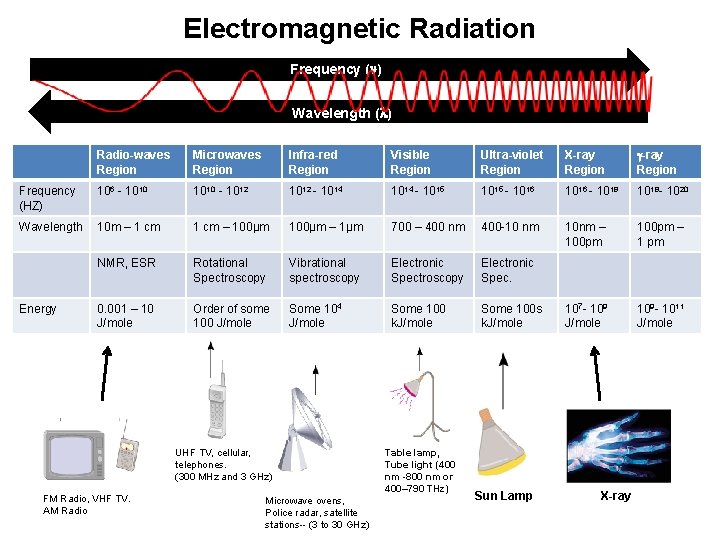
Electromagnetic Radiation Frequency ( ) Wavelength ( ) Radio-waves Region Microwaves Region Infra-red Region Visible Region Ultra-violet Region X-ray Region Frequency (HZ) 106 - 1010 - 1012 - 1014 - 1015 - 1016 - 1018 - 1020 Wavelength 10 m – 1 cm – 100µm – 1µm 700 – 400 nm 400 -10 nm 10 nm – 100 pm – 1 pm NMR, ESR Rotational Spectroscopy Vibrational spectroscopy Electronic Spec. 0. 001 – 10 J/mole Order of some 100 J/mole Some 104 J/mole Some 100 k. J/mole Some 100 s k. J/mole 107 - 109 J/mole 109 - 1011 J/mole Energy UHF TV, cellular, telephones. (300 MHz and 3 GHz) FM Radio, VHF TV. AM Radio Microwave ovens, Police radar, satellite stations-- (3 to 30 GHz) Table lamp, Tube light (400 nm -800 nm or 400– 790 THz) Sun Lamp X-ray

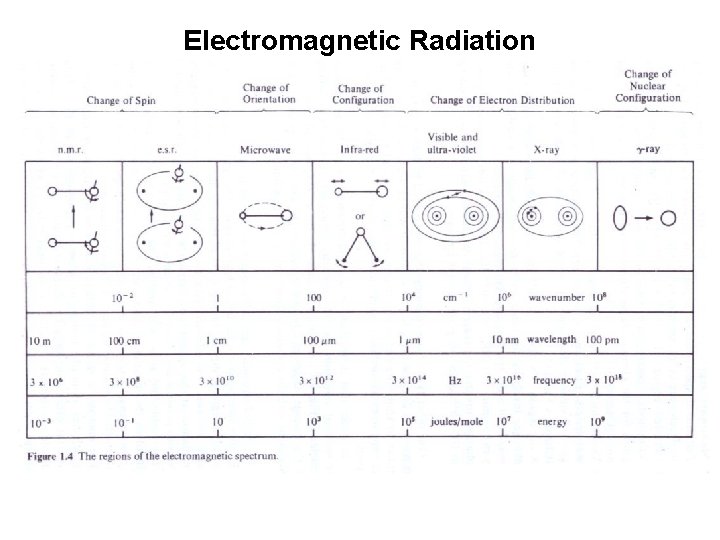
Electromagnetic Radiation

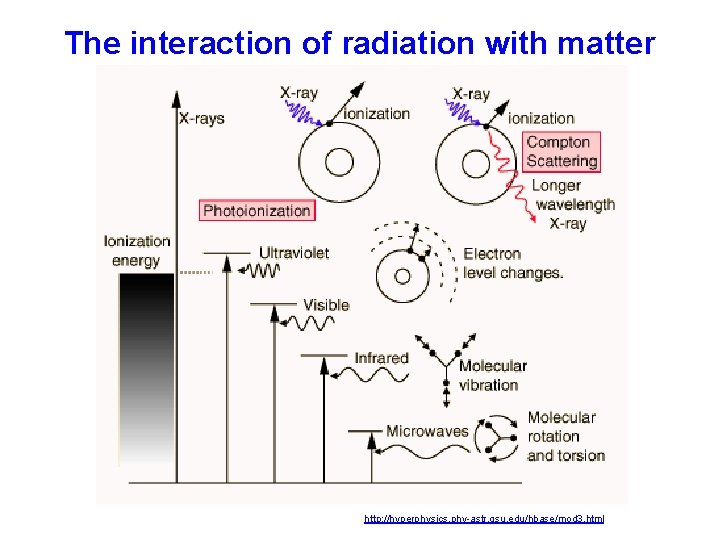
The interaction of radiation with matter http: //hyperphysics. phy-astr. gsu. edu/hbase/mod 3. html

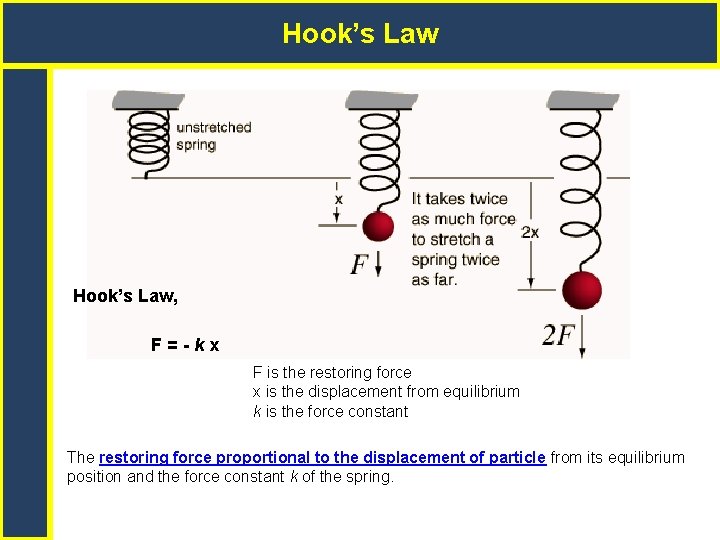
Hook’s Law, F=-kx F is the restoring force x is the displacement from equilibrium k is the force constant The restoring force proportional to the displacement of particle from its equilibrium position and the force constant k of the spring.

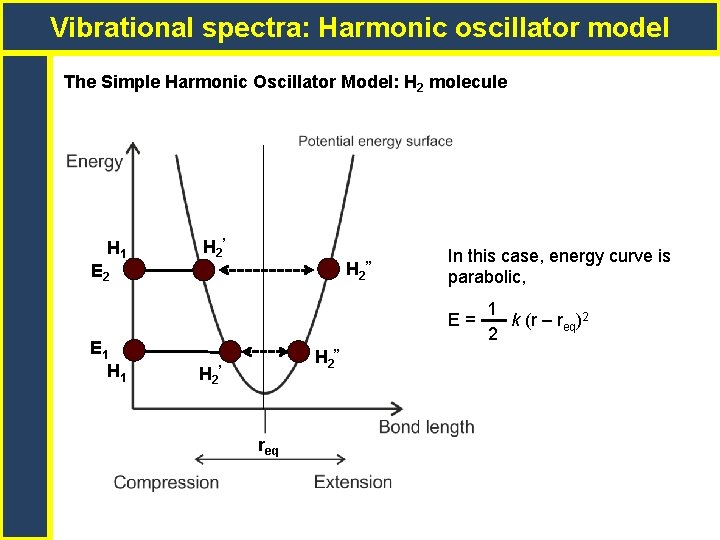
Vibrational spectra: Harmonic oscillator model The Simple Harmonic Oscillator Model: H 2 molecule H 1 H 2 ’ H 2 ” E 2 In this case, energy curve is parabolic, E= E 1 H 2 ” H 2 ’ req 1 k (r – req)2 2

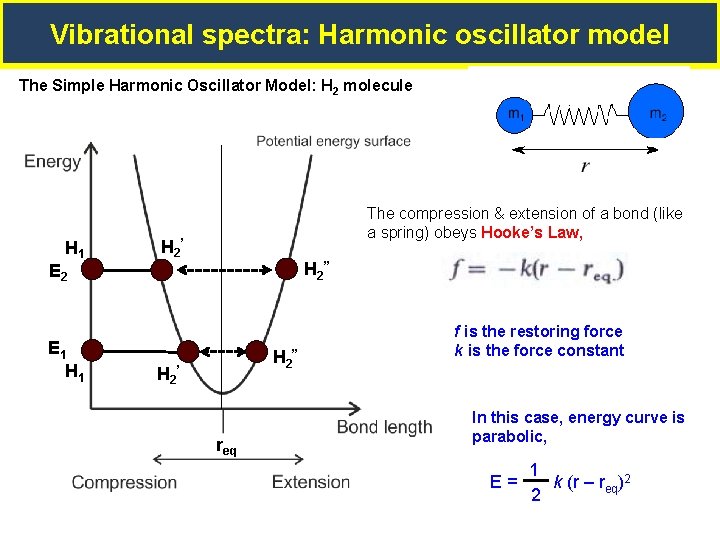
Vibrational spectra: Harmonic oscillator model The Simple Harmonic Oscillator Model: H 2 molecule H 1 The compression & extension of a bond (like a spring) obeys Hooke’s Law, H 2 ’ H 2 ” E 2 E 1 H 2 ” H 2 ’ req f is the restoring force k is the force constant In this case, energy curve is parabolic, 1 E= k (r – req)2 2

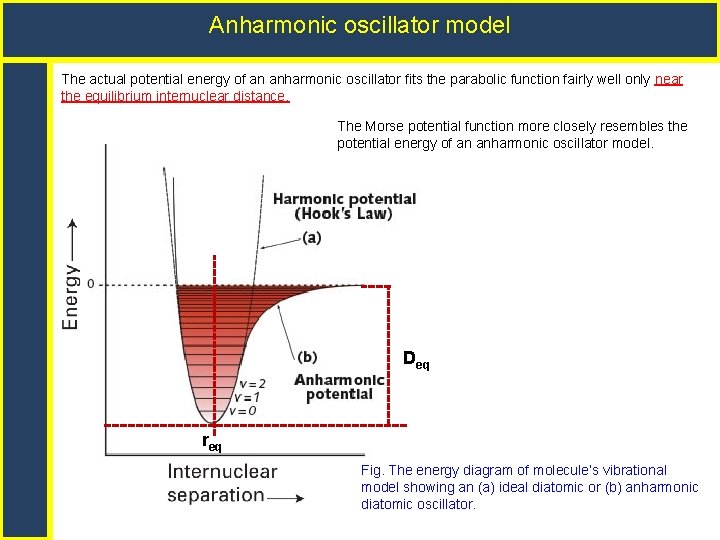
Anharmonic oscillator model The actual potential energy of an anharmonic oscillator fits the parabolic function fairly well only near the equilibrium internuclear distance. The Morse potential function more closely resembles the potential energy of an anharmonic oscillator model. Deq req Fig. The energy diagram of molecule’s vibrational model showing an (a) ideal diatomic or (b) anharmonic diatomic oscillator.

Vibrational spectra: Harmonic oscillator model Oscillation Frequency, k is the force constant = reduced mass, Vibrational frequency only dependent on the mass of the system and the force constant. From Schrodinger equation, Vibrational energies for simple harmonic oscillator,

Vibrational spectra: Harmonic oscillator model Oscillation Frequency, k is the force constant = reduced mass, The vibrational frequency is increasing with: v increasing force constant k ( = increasing bond strength) v decreasing atomic mass • Example: k c c > k c=c > k c-c

Infrared Spectroscopy POSITION REDUCED MASS LIGHT ATOMS HIGH FREQUENCY BOND STRENGTH (STIFFNESS) STRONG BONDS HIGH FREQUENCY The vibrational frequency is increasing with: • increasing force constant k (= increasing bond strength) • decreasing atomic mass

Vibrational spectra: Anharmonic oscillator model Vibrational energies for simple harmonic oscillators, ……… A Vibrational energies for anharmonic oscillators, ……… B

Different types of Energy Connecting macroscopic thermodynamics to a molecular understanding requires that we understand how energy is distributed on a molecular level. ATOMS: The electrons: Electronic energy. Increase the energy of one (or more) electrons in the atom. Nuclear motion: Translational energy. The atom can move around (translate) in space. MOLECULES: The electrons: Electronic energy. Increase the energy of one (or more) electrons in the molecule. Nuclear motion: Translational energy. The entire molecule can translate in space. Vibrational energy. The nuclei can move relative to one another. Rotational energy. The entire molecule can rotate in space.

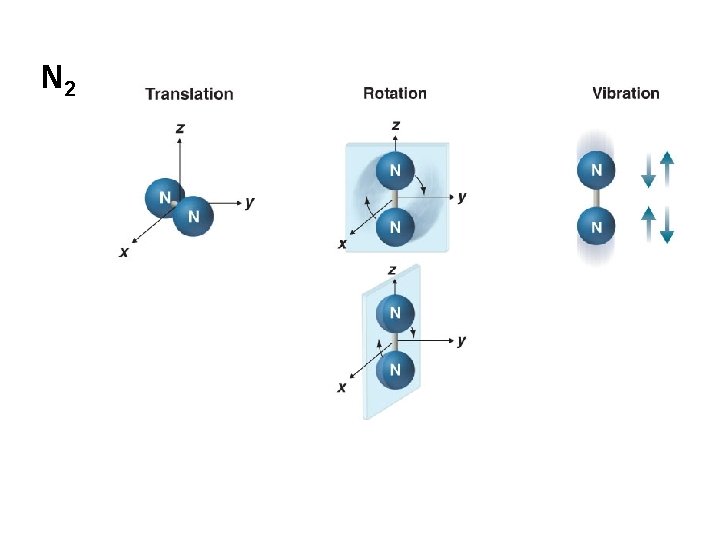
N 2

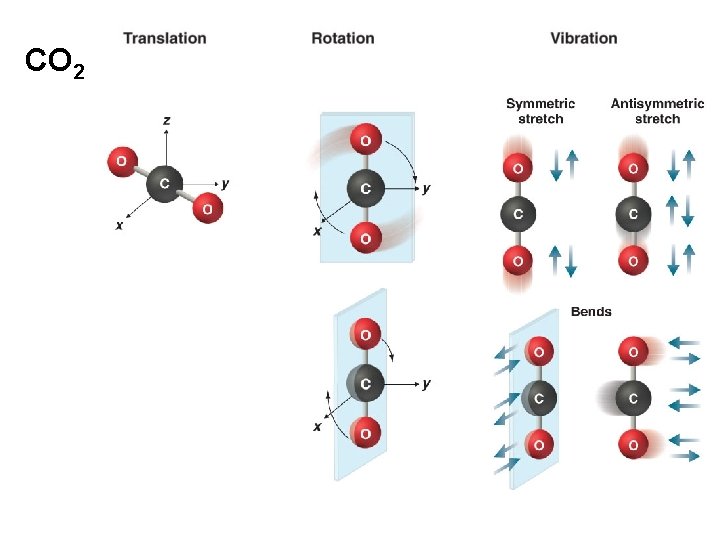
CO 2

Molecular vibrations q How many vibrations are possible (= fundamental vibrations)? A molecule has as many degrees of freedom as the total degree of freedom of its individual atoms. Each atom has three degrees of freedom (corresponding to the Cartesian coordinates), thus in an N-atom molecule there will be 3 N degree of freedom. In molecules, movements of the atoms are constrained by interactions through chemical bonds.

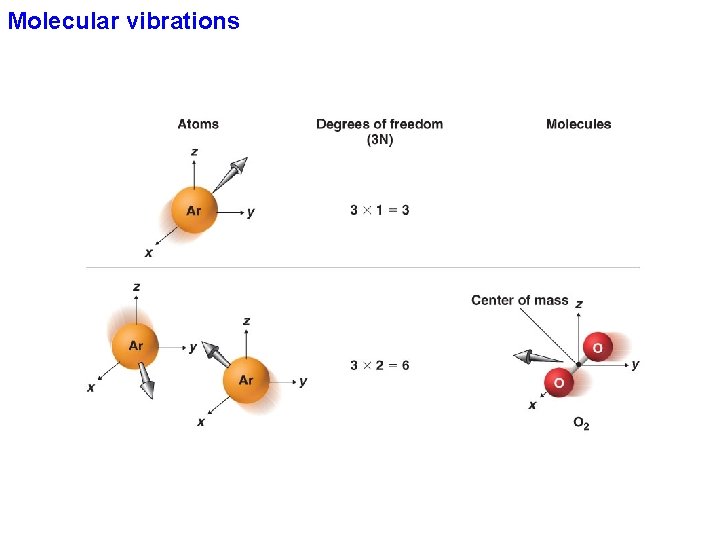
Molecular vibrations

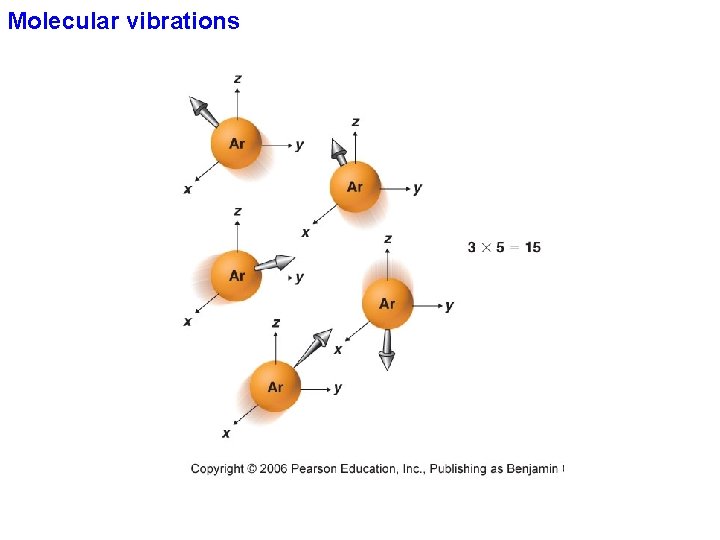
Molecular vibrations

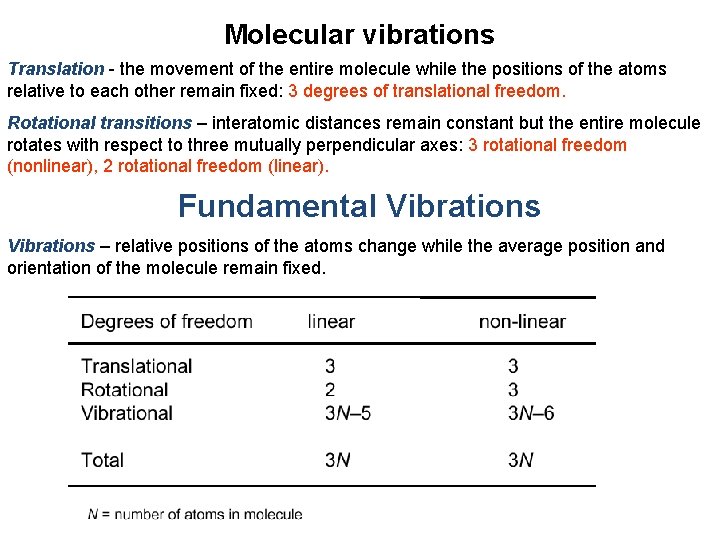
Molecular vibrations Translation - the movement of the entire molecule while the positions of the atoms relative to each other remain fixed: 3 degrees of translational freedom. Rotational transitions – interatomic distances remain constant but the entire molecule rotates with respect to three mutually perpendicular axes: 3 rotational freedom (nonlinear), 2 rotational freedom (linear). Fundamental Vibrations – relative positions of the atoms change while the average position and orientation of the molecule remain fixed.

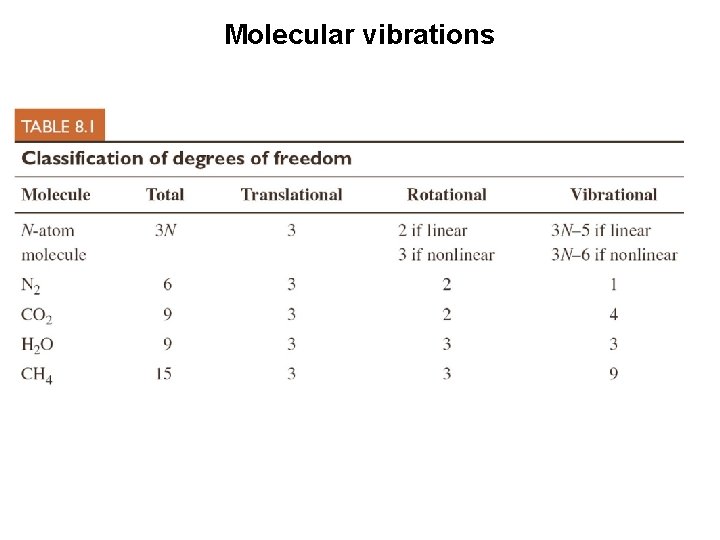
Molecular vibrations

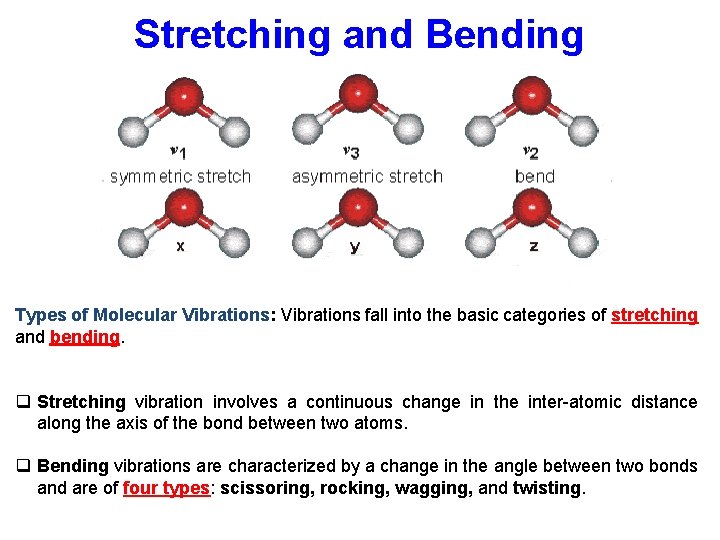
Stretching and Bending Types of Molecular Vibrations: Vibrations fall into the basic categories of stretching and bending. q Stretching vibration involves a continuous change in the inter-atomic distance along the axis of the bond between two atoms. q Bending vibrations are characterized by a change in the angle between two bonds and are of four types: scissoring, rocking, wagging, and twisting.

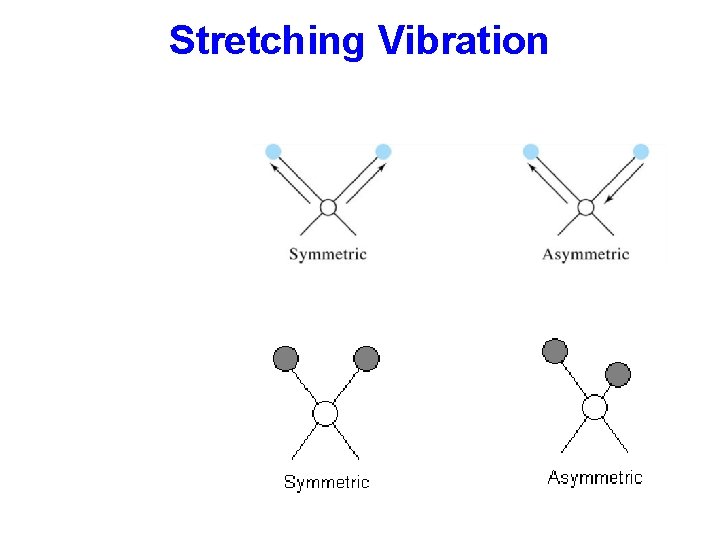
Stretching Vibration

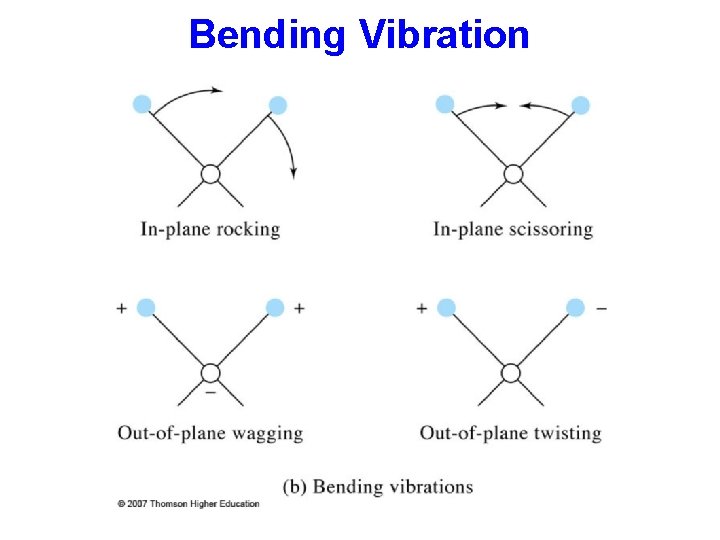
Bending Vibration

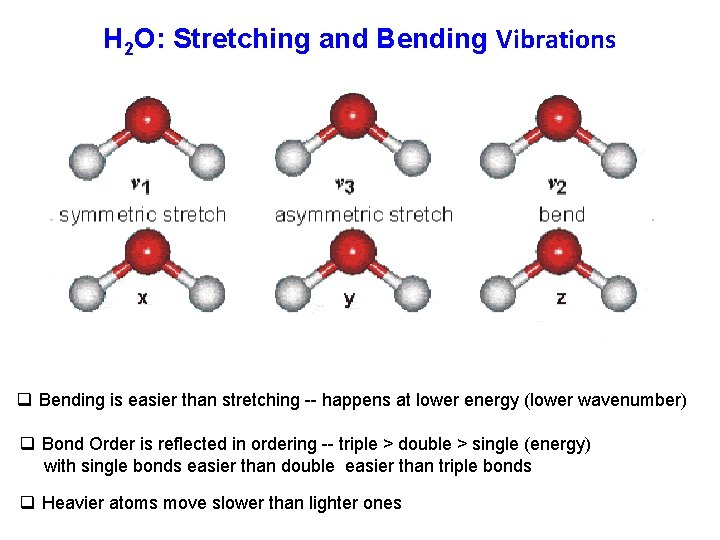
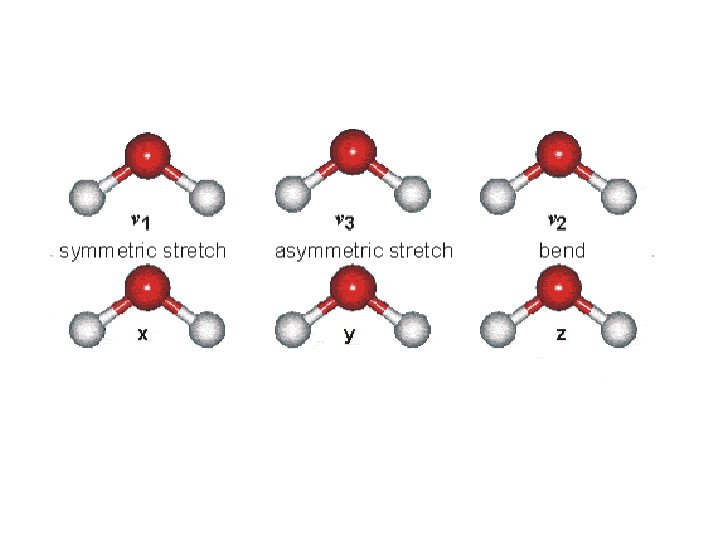
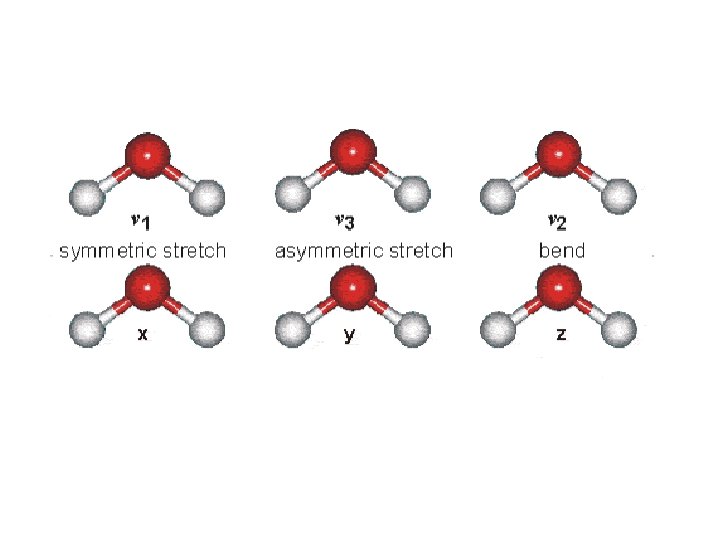
H 2 O: Stretching and Bending Vibrations q Bending is easier than stretching -- happens at lower energy (lower wavenumber) q Bond Order is reflected in ordering -- triple > double > single (energy) with single bonds easier than double easier than triple bonds q Heavier atoms move slower than lighter ones