INFORMS Annual Meeting 2006 Inexact SQP Methods for

INFORMS Annual Meeting 2006 Inexact SQP Methods for Equality Constrained Optimization Frank Edward Curtis Department of IE/MS, Northwestern University with Richard Byrd and Jorge Nocedal November 6, 2006

Outline n Introduction ¨ ¨ ¨ n Algorithm Development ¨ ¨ n Step computation Step acceptance Global Analysis ¨ ¨ n Problem formulation Motivation for inexactness Unconstrained optimization and nonlinear equations Merit function and sufficient decrease Satisfying first-order conditions Conclusions/Final remarks

Outline n Introduction ¨ ¨ ¨ n Algorithm Development ¨ ¨ n Step computation Step acceptance Global Analysis ¨ ¨ n Problem formulation Motivation for inexactness Unconstrained optimization and nonlinear equations Merit function and sufficient decrease Satisfying first-order conditions Conclusions/Final remarks

Equality constrained optimization Goal: solve the problem Define: the derivatives Define: the Lagrangian Goal: solve KKT conditions

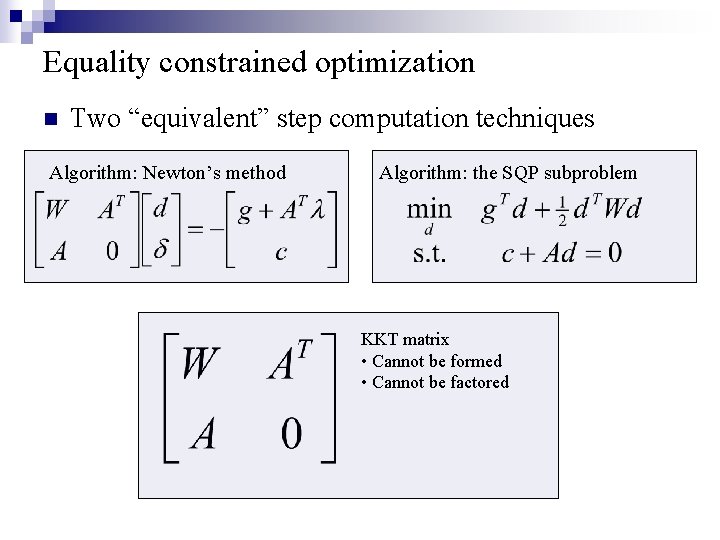
Equality constrained optimization n Two “equivalent” step computation techniques Algorithm: Newton’s method Algorithm: the SQP subproblem

Equality constrained optimization n Two “equivalent” step computation techniques Algorithm: Newton’s method Algorithm: the SQP subproblem KKT matrix • Cannot be formed • Cannot be factored

Equality constrained optimization n Two “equivalent” step computation techniques Algorithm: Newton’s method Algorithm: the SQP subproblem KKT matrix • Cannot be formed • Cannot be factored Linear system solve • Iterative method • Inexactness

Unconstrained optimization Goal: minimize a nonlinear objective Algorithm: Newton’s method (CG) Note: choosing any intermediate step ensures global convergence to a local solution of NLP (Steihaug, 1983)

Nonlinear equations Goal: solve a nonlinear system Algorithm: Newton’s method Note: choosing any step with and ensures global convergence (Dembo, Eisenstat, and Steihaug, 1982) (Eisenstat and Walker, 1994)

Outline n Introduction/Motivation ¨ ¨ ¨ n Algorithm Development ¨ ¨ n Step computation Step acceptance Global Analysis ¨ ¨ n Unconstrained optimization Nonlinear equations Constrained optimization Merit function and sufficient decrease Satisfying first-order conditions Conclusions/Final remarks

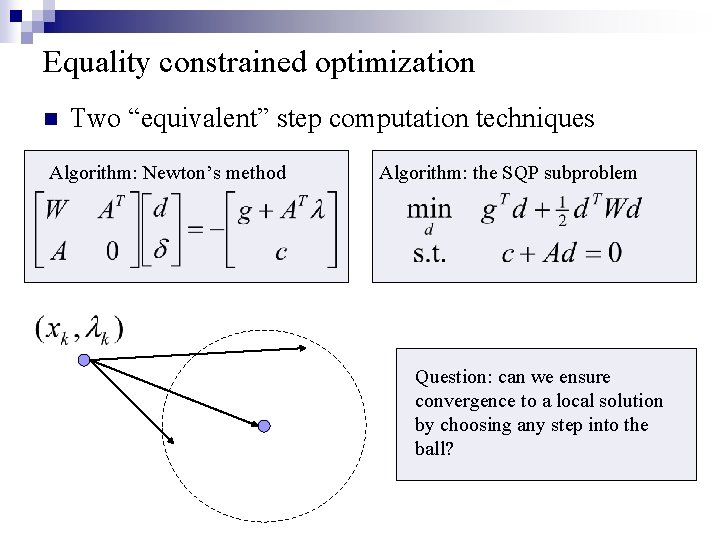
Equality constrained optimization n Two “equivalent” step computation techniques Algorithm: Newton’s method Algorithm: the SQP subproblem Question: can we ensure convergence to a local solution by choosing any step into the ball?

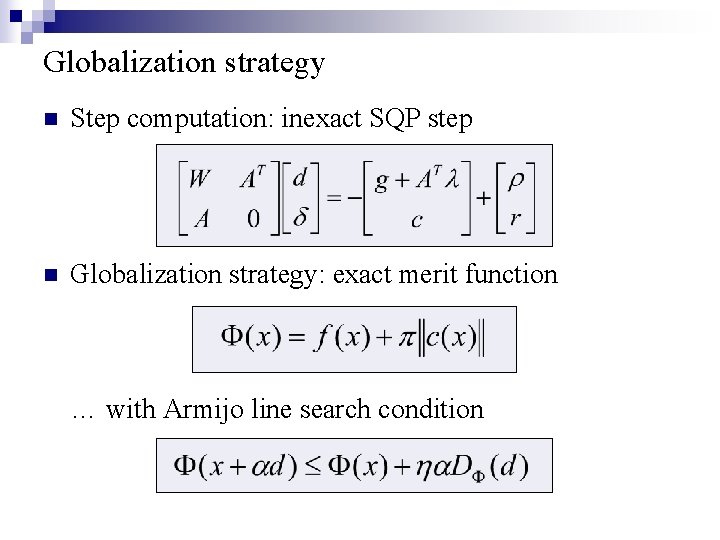
Globalization strategy n Step computation: inexact SQP step n Globalization strategy: exact merit function … with Armijo line search condition

First attempt n Proposition: sufficiently small residual n Test: 61 problems from CUTEr test set 1 e-8 1 e-7 1 e-6 1 e-5 1 e-4 1 e-3 1 e-2 1 e-1 Success 100% 97% 90% 85% 72% 38% Failure 0% 0% 3% 3% 10% 15% 28% 62%

First attempt… not robust n Proposition: sufficiently small residual n … not enough for complete robustness ¨ We have multiple goals (feasibility and optimality) ¨ Lagrange multipliers may be completely off

Second attempt n Step computation: inexact SQP step n Recall the line search condition n We can show

Second attempt n Step computation: inexact SQP step n Recall the line search condition n We can show . . . but how negative should this be?

Quadratic/linear model of merit function n Create model n Quantify reduction obtained from step

Quadratic/linear model of merit function n Create model n Quantify reduction obtained from step

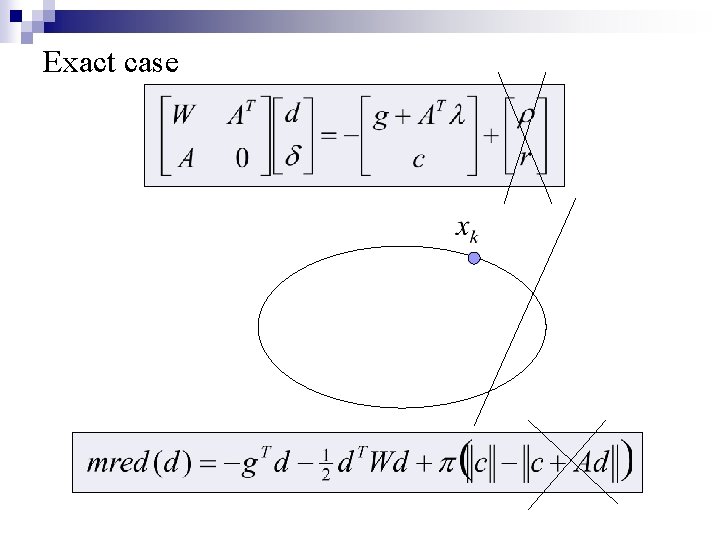
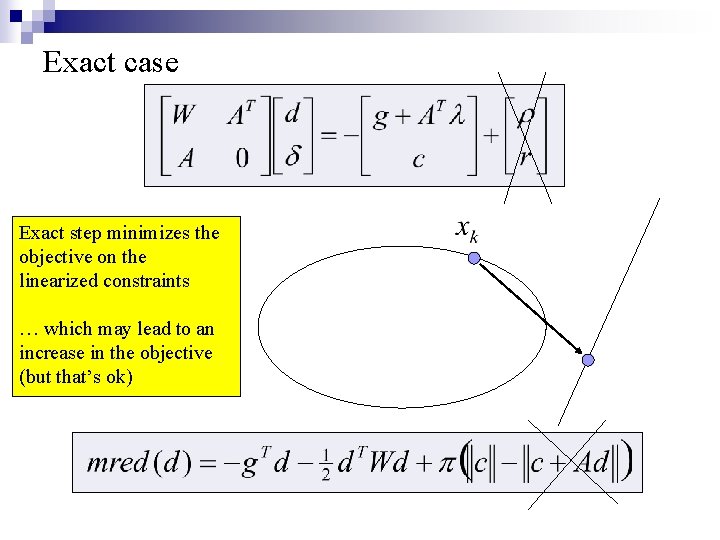
Exact case

Exact case Exact step minimizes the objective on the linearized constraints

Exact case Exact step minimizes the objective on the linearized constraints … which may lead to an increase in the objective (but that’s ok)

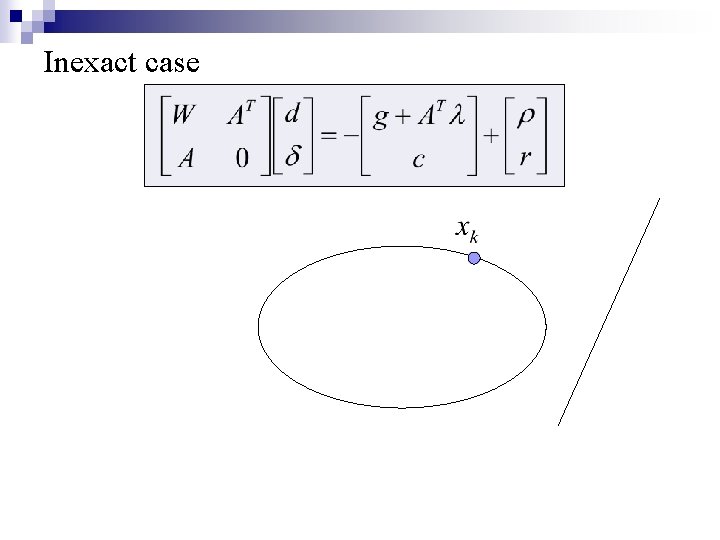
Inexact case

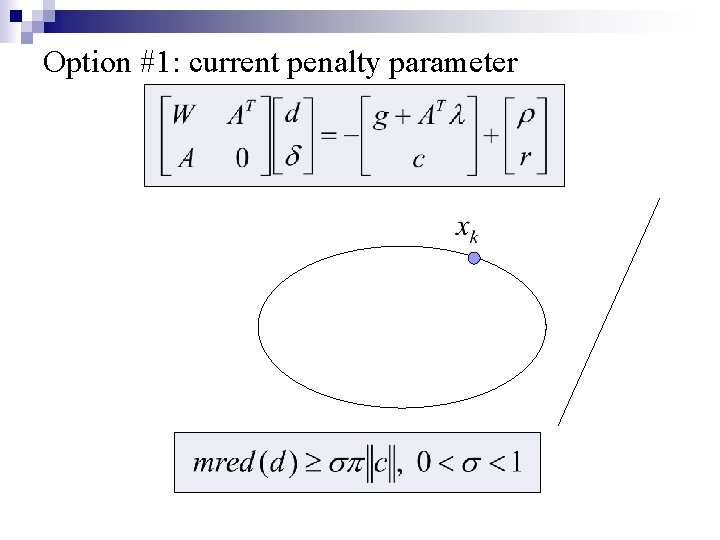
Option #1: current penalty parameter

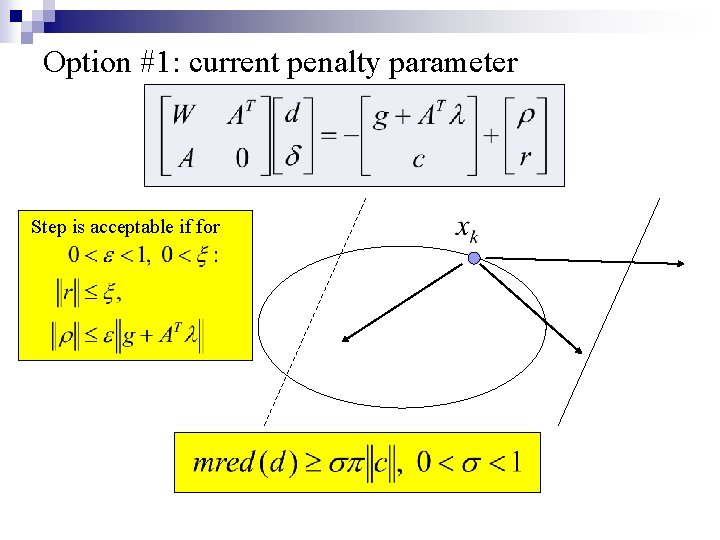
Option #1: current penalty parameter Step is acceptable if for

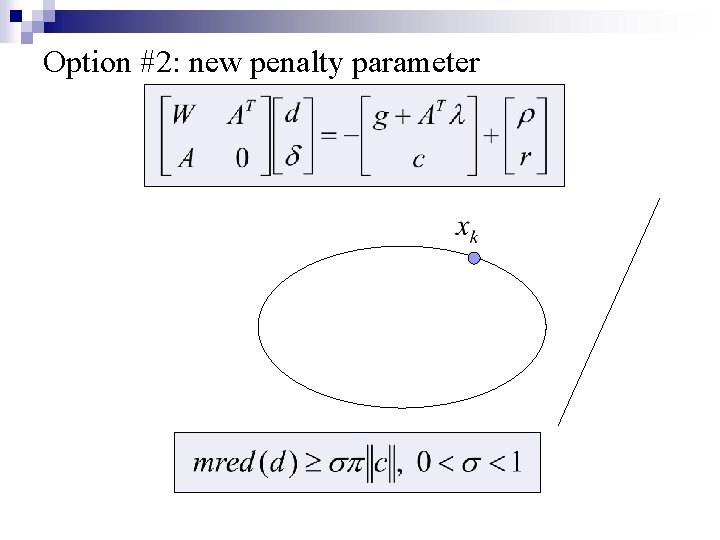
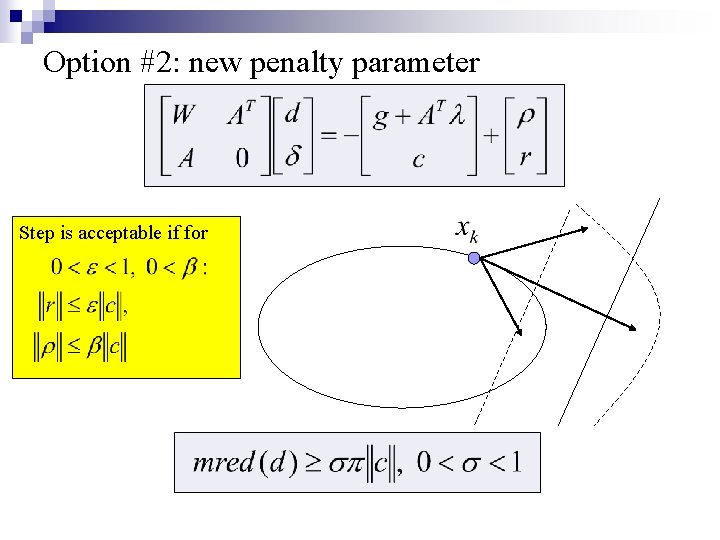
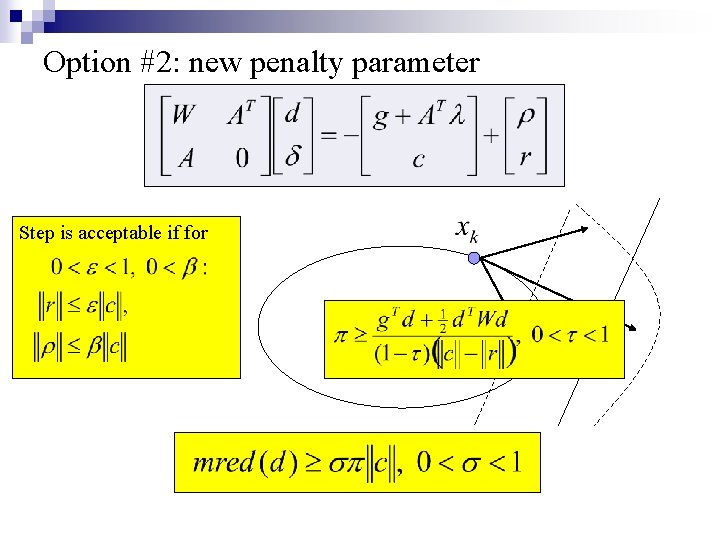
Option #2: new penalty parameter

Option #2: new penalty parameter Step is acceptable if for

Option #2: new penalty parameter Step is acceptable if for

Algorithm outline n for k = 0, 1, 2, … ¨ Iteratively solve ¨ Until or ¨ Update penalty parameter ¨ Perform backtracking line ¨ Update iterate search

Termination test n Observe KKT conditions

Outline n Introduction/Motivation ¨ ¨ ¨ n Algorithm Development ¨ ¨ n Step computation Step acceptance Global Analysis ¨ ¨ n Unconstrained optimization Nonlinear equations Constrained optimization Merit function and sufficient decrease Satisfying first-order conditions Conclusions/Final remarks

Assumptions n The sequence of iterates is contained in a convex set over which the following hold: ¨ the objective function is bounded below objective and constraint functions and their first and second derivatives are uniformly bounded in norm ¨ the constraint Jacobian has full row rank and its smallest singular value is bounded below by a positive constant ¨ the Hessian of the Lagrangian is positive definite with smallest eigenvalue bounded below by a positive constant

Sufficient reduction to sufficient decrease n Taylor expansion of merit function yields n Accepted step satisfies

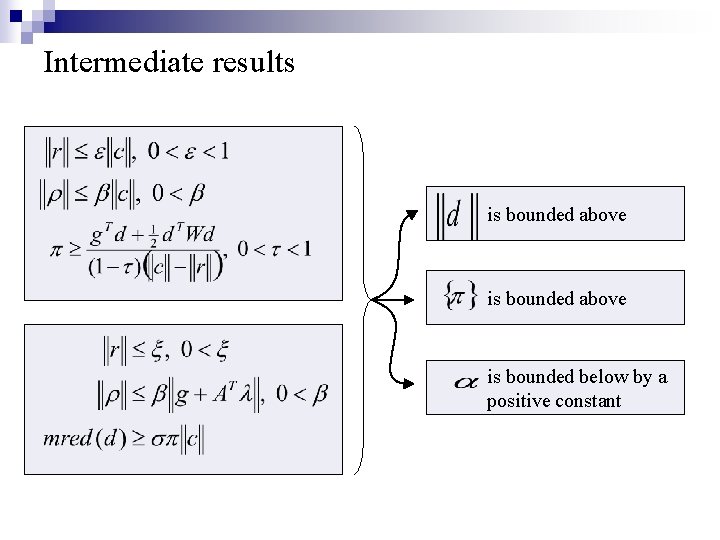
Intermediate results is bounded above is bounded below by a positive constant

Sufficient decrease in merit function

Step in dual space n We converge to an optimal primal solution, and (for sufficiently small Therefore, and )

Outline n Introduction/Motivation ¨ ¨ ¨ n Algorithm Development ¨ ¨ n Step computation Step acceptance Global Analysis ¨ ¨ n Unconstrained optimization Nonlinear equations Constrained optimization Merit function and sufficient decrease Satisfying first-order conditions Conclusions/Final remarks

Conclusion/Final remarks n Review ¨ Defined a globally convergent inexact SQP algorithm ¨ Require only inexact solutions of KKT system ¨ Require only matrix-vector products involving objective and constraint function derivatives ¨ Results also apply when only reduced Hessian of Lagrangian is assumed to be positive definite n Future challenges ¨ Implementation and appropriate parameter ¨ Nearly-singular constraint Jacobian ¨ Inexact derivative information ¨ Negative curvature ¨ etc. , etc…. values