InformationTheoretic Co Clustering Inderjit S Dhillon et al

Information-Theoretic Co. Clustering Inderjit S. Dhillon et al. University of Texas, Austin presented by Xuanhui Wang

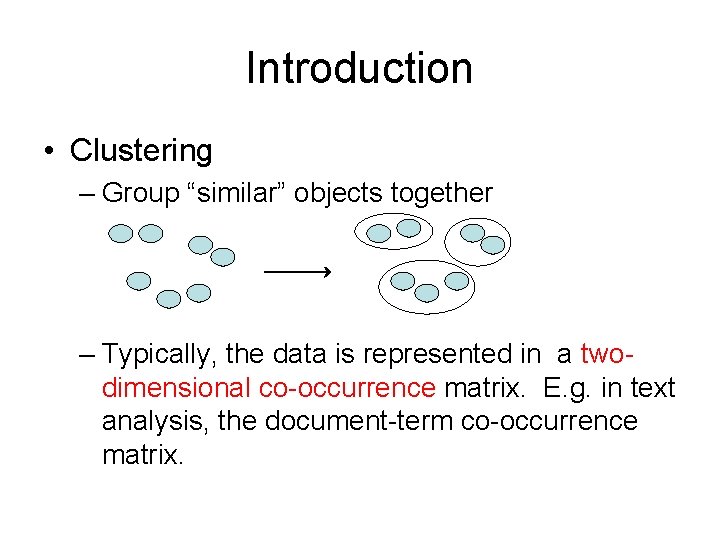
Introduction • Clustering – Group “similar” objects together – Typically, the data is represented in a twodimensional co-occurrence matrix. E. g. in text analysis, the document-term co-occurrence matrix.

One-dimensional Clustering Document Clustering: ØTreat each row as one Doc ØDefine a similarity measure ØClustering the documents using e. g. k-means Term Clustering: ØSymmetric with Doc Clustering Doc-Term Co-occurrence Matrix

Idea of Co-Clustering • Co-occurrence Matrices Characteristics – Data sparseness – High dimension – Noise • Motivation – Is it possible to combine the document and term clustering together? Can they bootstrap each other? • Yes, Co-Clustering – Simultaneously cluster the rows X and columns Y of the co-occurrence matrix.

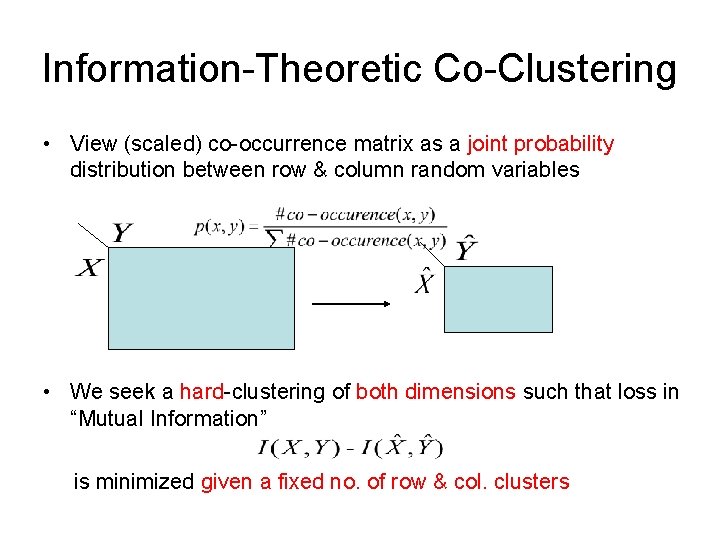
Information-Theoretic Co-Clustering • View (scaled) co-occurrence matrix as a joint probability distribution between row & column random variables • We seek a hard-clustering of both dimensions such that loss in “Mutual Information” is minimized given a fixed no. of row & col. clusters

Example • Mutual Information between random variables X and Y: It can be verified that this is the minimum mutual information loss

Information Theoretic Co-clustering • (Lemma) Loss in mutual information equals where – Can be shown that q(x, y) is a “maximum entropy” approximation to p(x, y). – q(x, y) preserves marginals : q(x)=p(x) & q(y)=p(y)

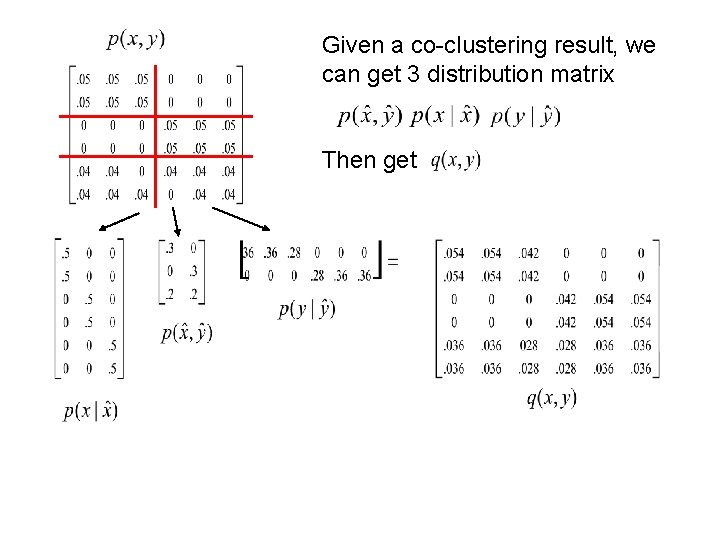
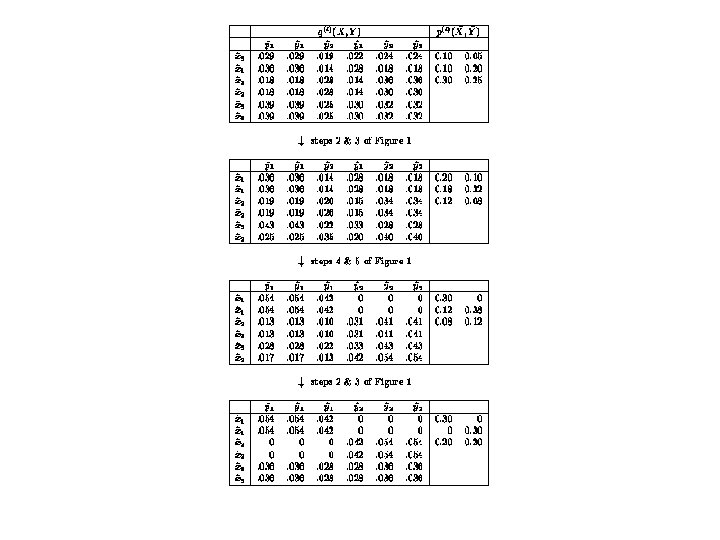
Given a co-clustering result, we can get 3 distribution matrix Then get

Preserving Mutual Information • Lemma: Note that may be thought of as the “prototype” of row cluster (the usual “centroid” of the cluster is ) Similarly,

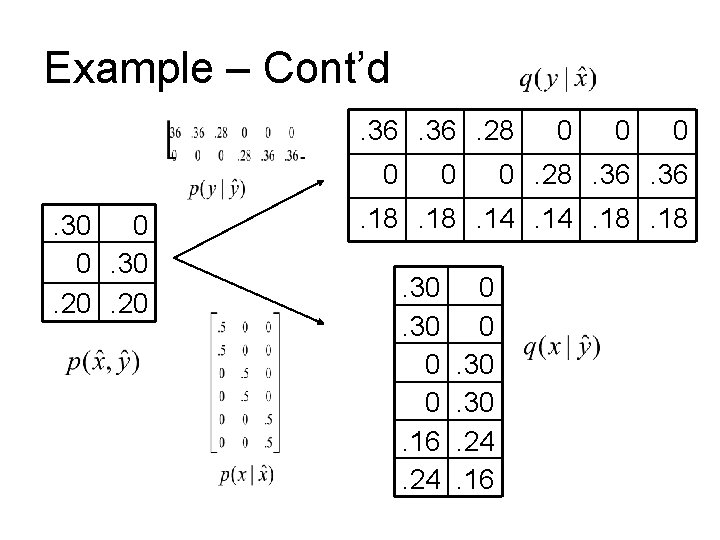
Example – Cont’d. 36. 28 0. 30 0 0. 30. 20 0 0 0. 28. 36 . 18. 14. 18. 30 0 0. 16. 24 0 0. 30. 24. 16

Co-Clustering Algorithm • 1. Given a partition, calculate the “prototype” of each row cluster. • 2. Assign each row x to its nearest cluster. • 3. Update the probabilities based on the new row clusters and then compute new column cluster “prototype”. • 4. Assign each column y to its nearest cluster. • 5. Update the probabilities based on the new column clusters and then compute new row cluster “prototype”. • 6. If converge, stop. Otherwise go to Step 2.

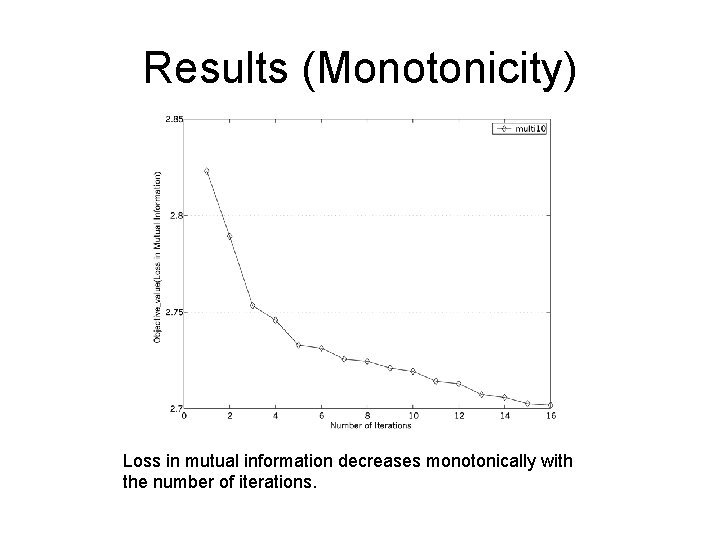
Properties of Co-clustering Algorithm • Theorem: The co-clustering algorithm monotonically decreases loss in mutual information (objective function value) • Marginals p(x) and p(y) are preserved at every step (q(x)=p(x) and q(y)=p(y) )

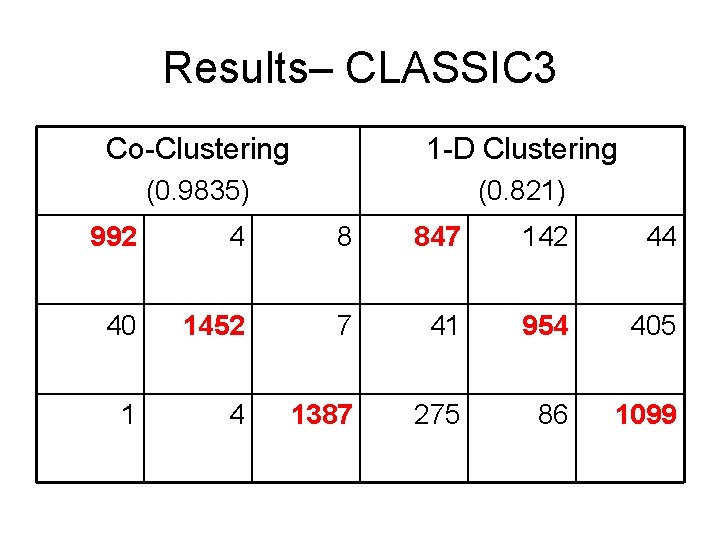
Experiments • Data sets – 20 Newsgroups data • 20 classes, 20000 documents – Classic 3 data set • 3 classes (cisi, med and cran), 3893 documents

Results– CLASSIC 3 Co-Clustering 1 -D Clustering (0. 9835) (0. 821) 992 4 8 847 142 44 40 1452 7 41 954 405 1 4 1387 275 86 1099

Results (Monotonicity) Loss in mutual information decreases monotonically with the number of iterations.

Conclusions • Information theoretic approaches to clustering, co-clustering. • Co-clustering intertwines row and column clusterings at all stages and is guaranteed to reach a local minimum. • Can deal with the high-dimensional, sparse data efficiently.

Remarks • Theoretically solid paper! Great! • It is like k-means or EM in spirit. But it uses different formula to compute the cluster “prototype” (centroid in k-means). • It needs to specify the number of clusters of row and column in advance.

Thank you!