Informationsteknologi Todays class n Geometric objects and transformations

Informationsteknologi Today’s class n Geometric objects and transformations Wednesday, November 7, 2007 Computer Graphics - Class 5 1

Informationsteknologi Vector operations n Review of vector operations needed for working in computer graphics ® adding two vectors ® subtracting two vectors ® scaling a vector ® magnitude of a vector ® normalizing a vector Wednesday, November 7, 2007 Computer Graphics - Class 5 2

Informationsteknologi Linear combination of vectors n n n Convex combinations (coefficients of linear combination are all non-negative and add up to 1) Important convex combination: p(t) = a(1 -t) + b(t) where a and b are vectors and 0 t 1 If a and b are points, then p(t) = a(1 -t) + b(t) is said to interpolate the points a and b (0 t 1) Wednesday, November 7, 2007 Computer Graphics - Class 5 3

Informationsteknologi Convex sets and hulls n n A convex set of points is a collection of points in which the line connecting any pair in the set lies entirely in the set Examples: circle ® rectangle ® n A convex hull is the smallest convex set that contains a specified collection of points Wednesday, November 7, 2007 Computer Graphics - Class 5 4

Informationsteknologi Dot products n n n cos = ua • ub Vectors are orthogonal if dot product is 0 Vectors are less than 90° apart if dot product is positive Vectors are more than 90° apart if dot product is negative Perpendicular projection of a onto b is (a • ub) ub Reflected ray is a - 2(a • un) un where un is a unit normal vector to the surface Wednesday, November 7, 2007 Computer Graphics - Class 5 5

Informationsteknologi Cross products n u = (ux, uy, uz), v = (vx, vy, vz) n u x v is perpendicular to both u and v n Orientation follows the right hand rule n n Wednesday, November 7, 2007 Computer Graphics - Class 5 6

Informationsteknologi Polygons A polygon is a defined by a set of vertices and edges n An interior angle of a polygon is an angle formed by two adjacent edges that is inside the boundary n A convex polygon has every interior angle < 180° n A concave polygon is a polygon that is not convex n Wednesday, November 7, 2007 Computer Graphics - Class 5 7

Informationsteknologi Identifying concave polygons n n Concave polygons will have at least one interior angle > 180° The sin of this angle will be negative Thus, the “magnitude” of the cross product of the two vectors (edges) forming this angle will be negative This will also manifest itself by some z components of the cross product being positive and others being negative Wednesday, November 7, 2007 Computer Graphics - Class 5 8

Informationsteknologi Splitting concave polygons n n n Concave polygons present problems for computer graphics Splitting them up will get us convex polygons Define edge vector Ek as the vector Vk+1 -Vk, where the V’s are adjacent vertices Calculate the edge cross products in order counter-clockwise around the polygon If any z component of a cross product is negative the polygon is concave and can be split along the line from the first edge in the cross product Wednesday, November 7, 2007 Computer Graphics - Class 5 9

Informationsteknologi Triangularization n n A convex polygon can easily be triangularized (sometimes also referred to as tessellated) Define three consecutive vertices of the polygon as a triangle Remove the middle vertex from the polygon’s vertex list Repeat with the modified list until only three vertices remain, forming the last triangle Wednesday, November 7, 2007 Computer Graphics - Class 5 10

Informationsteknologi Is a point inside a polygon? n Even-odd test: construct a line from point to a point known to be outside polygon ® count # of intersections of line with boundary ® if odd, point is inside ® if crossing occurs at a vertex ® § look at endpoints of the edges that meet § if both endpoints are on same side of line segment then the vertex counts as an even number of crossings, otherwise it counts as an odd number Wednesday, November 7, 2007 Computer Graphics - Class 5 11

Informationsteknologi N-gons n An n-gon is a regular polygon of n sides Wednesday, November 7, 2007 Computer Graphics - Class 5 12

Informationsteknologi Rosettes n Rosettes are n-gons where each vertex has been joined to each other vertex Wednesday, November 7, 2007 Computer Graphics - Class 5 13

Informationsteknologi A cube Consider a cube n Pair off and come up with: n ®A set of vertices for the cube ® A sequence of Open. GL statements to draw the cube ® How many function calls are you making? Wednesday, November 7, 2007 Computer Graphics - Class 5 14

Informationsteknologi Vertex arrays n n Allow you to specify geometry with much fewer function calls For example, the cube can be drawn in just one function call Create an array of vertex data and use gl. Vertex. Pointer() to refer to it Need to enable this with gl. Enable. Client. State (GL_VERTEX_ARRAY); Wednesday, November 7, 2007 Computer Graphics - Class 5 15

Informationsteknologi gl. Vertex. Pointer() n Four parameters: ® Size: number of coordinates per vertex; must be 2, 3, or 4 ® Type: the data type of each coordinate in the array ® Stride: the byte offset between consecutive vertices (frequently 0) ® Pointer: a pointer to the first coordinate of the first vertex in the array Wednesday, November 7, 2007 Computer Graphics - Class 5 16

Informationsteknologi Index array Need a second array with indices into the vertex array to specify which vertices make up each face of your geometry n gl. Draw. Elements() is then used to draw the geometry n Wednesday, November 7, 2007 Computer Graphics - Class 5 17

Informationsteknologi gl. Draw. Elements() n Four parameters: Mode: specified what kind of geometric primitives to render ® Count: number of vertices in the index array to be rendered ® Type: the type of the values in the index array; must be one of GL_UNSIGNED_BYTE, GL_UNSIGNED_SHORT, or GL_UNSIGNED_INT ® Indices: a pointer to the array of indices into the vertex array ® Wednesday, November 7, 2007 Computer Graphics - Class 5 18

Informationsteknologi Example program n rotating. Cube. c demonstrates vertex arrays and introduces the idle callback function Wednesday, November 7, 2007 Computer Graphics - Class 5 19

Informationsteknologi Transformation matrices A transformation matrix is a matrix that transforms a point to another point n In 2 -dimensions, this has the following algebraic form: n Wednesday, November 7, 2007 Computer Graphics - Class 5 20

Informationsteknologi Uniform scaling n Given a scale factor s > 0, a matrix which produces a uniform scaling is n Example: Wednesday, November 7, 2007 Computer Graphics - Class 5 21

Informationsteknologi Non-uniform scaling n Given scale factors sx > 0 and sy > 0, a matrix which produces non-uniform scaling is n Example: Wednesday, November 7, 2007 Computer Graphics - Class 5 22

Informationsteknologi Comparison of scalings Uniform scaling preserves shape n Non-uniform scaling introduces distortion n Wednesday, November 7, 2007 Computer Graphics - Class 5 23

Informationsteknologi Two scalings in a row n Two scalings in a row have a multiplicative effect ® P’ = S 1 P ® P’’ = S 2 P’ = S 2 S 1 P n Note the order of the scales appears to be reversed (S 2 before S 1), but it’s not Wednesday, November 7, 2007 Computer Graphics - Class 5 24

Informationsteknologi Composite transformation matrix The product of two or more transformation matrices is known as a composite transformation matrix n For our two scalings we have n Wednesday, November 7, 2007 Computer Graphics - Class 5 25

Informationsteknologi A side effect Note that an object which does not have the origin inside it will be moved as well by a scaling n We will see how to correct this effect shortly n Wednesday, November 7, 2007 Computer Graphics - Class 5 26

Informationsteknologi Reflections n Reflection through the x-axis negates the y coordinate: n Reflection through the y-axis negates the x coordinate: Wednesday, November 7, 2007 Computer Graphics - Class 5 27

Informationsteknologi Rotation transforms a point in a circular manner n Positive angles imply a counter-clockwise rotation n Wednesday, November 7, 2007 Computer Graphics - Class 5 28

Informationsteknologi The geometry of rotation (x’, y’) r r (x, y) = (r cos , r sin ) (x’, y’) = (r cos ( + ), r sin ( + )) Wednesday, November 7, 2007 Computer Graphics - Class 5 29

Informationsteknologi Rotation formula (x, y) = (r cos , r sin ) n (x’, y’) = (r cos ( + ), r sin ( + )) n Recall sum of angle trig formulas: n ( + ) = sin cos + cos sin ® cos ( + ) = cos - sin ® sin x’ = r (cos - sin ) = x cos y sin n y’ = r (sin cos + cos sin ) = y cos + x sin = x sin + y cos n Wednesday, November 7, 2007 Computer Graphics - Class 5 30

Informationsteknologi Rotation matrix n Results from the previous slide give the matrix for rotation: Wednesday, November 7, 2007 Computer Graphics - Class 5 31

Informationsteknologi Two rotations in a row n Two rotations in a row have an additive effect on the angles P’ = R 1 P ® P’’ = R 2 P’ = R 2 R 1 P ® Wednesday, November 7, 2007 Computer Graphics - Class 5 32

Informationsteknologi Reflection through y=x 45° n n n Rotate point -45° so that reflection line is x-axis Reflect through x-axis Rotate 45° back Wednesday, November 7, 2007 Computer Graphics - Class 5 33

Informationsteknologi 1. Rotate -45° n Recall matrix to perform rotation: n Fill in = -45°: Wednesday, November 7, 2007 Computer Graphics - Class 5 34

Informationsteknologi 2. Reflect through x-axis n Recall matrix for x-axis reflection: Wednesday, November 7, 2007 Computer Graphics - Class 5 35

Informationsteknologi 3. Rotate back n Recall matrix to perform rotation: n Fill in = 45°: Wednesday, November 7, 2007 Computer Graphics - Class 5 36

Informationsteknologi Compute the total transformation n Take each transformation matrix in the order the transformations need to be applied and multiply them together: Wednesday, November 7, 2007 Computer Graphics - Class 5 37

Informationsteknologi Result n The result of reflecting a point through y=x is the switching of the x and y coordinates of the point Wednesday, November 7, 2007 Computer Graphics - Class 5 38

Informationsteknologi Another transformation n Find the transformation that reflects a point through the line y = 2. y=2 Wednesday, November 7, 2007 Computer Graphics - Class 5 39

Informationsteknologi The steps Translate by -2 in the y direction n Reflect through the x-axis n Translate back n Wednesday, November 7, 2007 Computer Graphics - Class 5 40

Informationsteknologi Translation n Translation is a transformation that results in a linear movement of a point Wednesday, November 7, 2007 Computer Graphics - Class 5 41

Informationsteknologi A problem with translation Every other transformation we have looked at could be expressed using a 2 2 matrix and multiplying the point by the matrix n Translation cannot be expressed this way as we need to add fixed amounts to the x and y coordinates n Wednesday, November 7, 2007 Computer Graphics - Class 5 42

Informationsteknologi A solution So that translation behaves like our other transformations we want to express it using a matrix and multiplying the point by the matrix n Will need to add an extra coordinate to our point n This coordinate will have the value 1 n Wednesday, November 7, 2007 Computer Graphics - Class 5 43

Informationsteknologi Translation matrix n The matrix for doing a translation is n Example: Wednesday, November 7, 2007 Computer Graphics - Class 5 44

Informationsteknologi Homogeneous coordinates This new representation for our points (with the 1 in the extra coordinate) is known as homogeneous coordinates n There are times when the homogeneous coordinate is not 1; we’ll see this in perspective projections n Wednesday, November 7, 2007 Computer Graphics - Class 5 45

Informationsteknologi New versions of transformation matrices Homogeneous coordinates requires a change in the transformation matrices to accommodate the extra coordinate n Matrices will now be 3 3 n Example: uniform scaling n Wednesday, November 7, 2007 Computer Graphics - Class 5 46

Informationsteknologi The transformations for our problem n Translate by -2 in y n Reflect through x-axis n Translate by +2 in y Wednesday, November 7, 2007 Computer Graphics - Class 5 47

Informationsteknologi The composite transformation n The composite transformation for reflecting a point through the line y=2 is found by multiplying CBA: Wednesday, November 7, 2007 Computer Graphics - Class 5 48

Informationsteknologi Rotations about an arbitrary point The rotations we have considered so far all occur around the origin n Suppose you had the following figure, which you would like to rotate about its center: n Wednesday, November 7, 2007 Computer Graphics - Class 5 49

Informationsteknologi Rotation analysis If we applied the rotation transformation as we currently have it, the square would rotate about the origin n This is not what we want n We want the square to rotate in place n Thus, we need to make the center of the square the point of rotation n Wednesday, November 7, 2007 Computer Graphics - Class 5 50

Informationsteknologi Fixed points We call the point about which we want to rotate a fixed point as it will not change its position during the transformation n The same concept can be applied to scaling as well n Wednesday, November 7, 2007 Computer Graphics - Class 5 51

Informationsteknologi Steps for arbitrary rotation n Translate the fixed point to the origin n Perform the rotation around the origin n Translate the fixed point back to its position Wednesday, November 7, 2007 Computer Graphics - Class 5 52

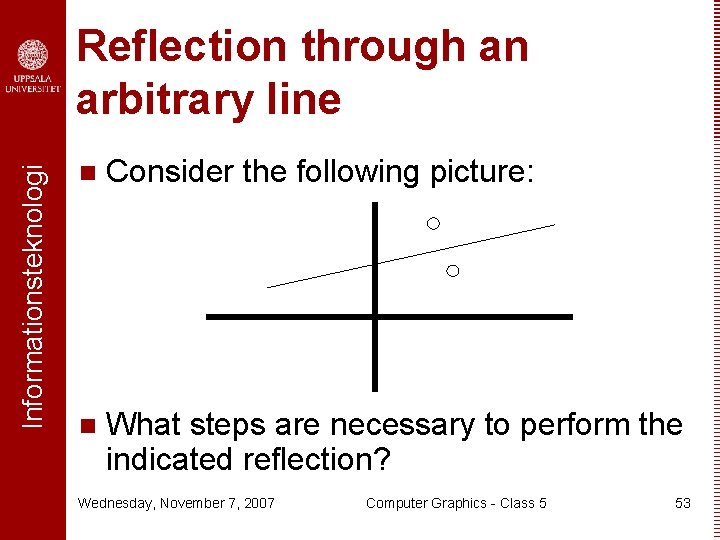
Informationsteknologi Reflection through an arbitrary line n Consider the following picture: n What steps are necessary to perform the indicated reflection? Wednesday, November 7, 2007 Computer Graphics - Class 5 53

Informationsteknologi Arbitrary reflection transformation n Sequence for arbitrary reflection: ® Translate line by its y-intercept so that it goes through origin (T) ® Rotate around origin so line lies on x-axis (R) ® Reflect through x-axis (X) ® Rotate back (R-1) ® Translate back (T-1) n Composite: T-1 R-1 XRT Wednesday, November 7, 2007 Computer Graphics - Class 5 54