Information Theory of Wireless Networks David Tse Wireless

Information Theory of Wireless Networks David Tse Wireless Foundations U. C. Berkeley Information Theory Summer School Penn State June 3, 2008

The Holy Grail • Shannon’s information theory provides the basis for all modern-day communication systems. • His original theory was point-to-point. • After 60 years we are still very far away from generalizing theory to networks. • We propose approaches to make progress in the context of wireless networks.

Modeling the Wireless Medium • broadcast • interference • high dynamic range in channel strengths between different nodes • Basic model: additive Gaussian channel:

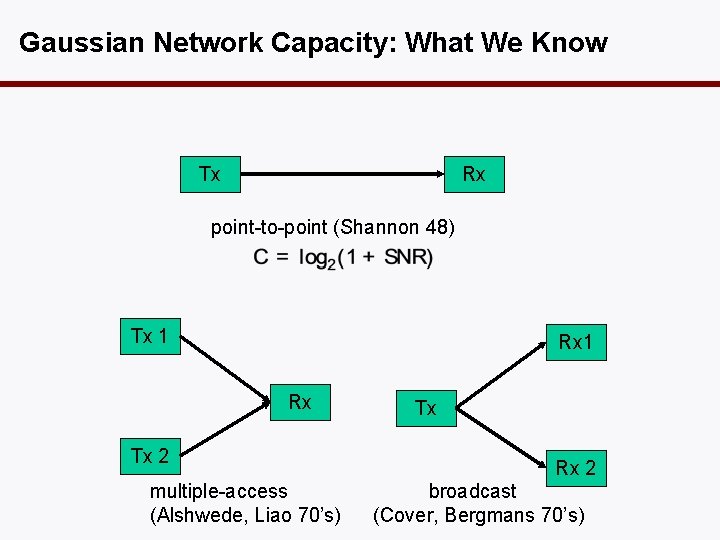
Gaussian Network Capacity: What We Know Tx Rx point-to-point (Shannon 48) Tx 1 Rx Tx 2 multiple-access (Alshwede, Liao 70’s) Tx Rx 2 broadcast (Cover, Bergmans 70’s)

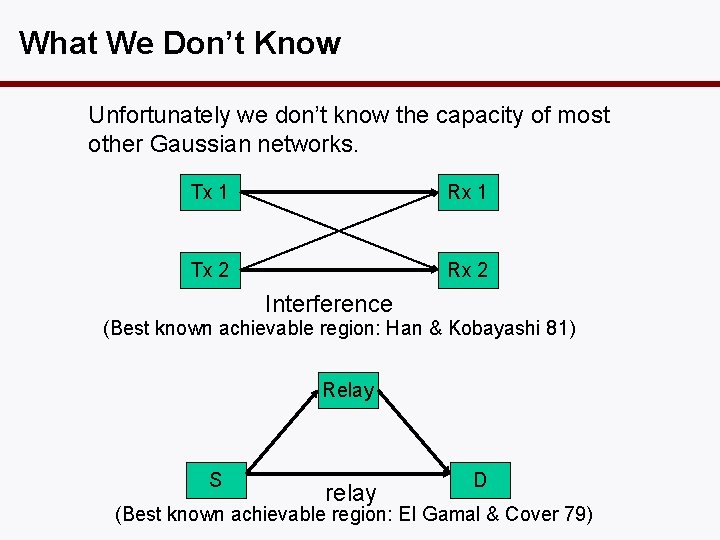
What We Don’t Know Unfortunately we don’t know the capacity of most other Gaussian networks. Tx 1 Rx 1 Tx 2 Rx 2 Interference (Best known achievable region: Han & Kobayashi 81) Relay S relay D (Best known achievable region: El Gamal & Cover 79)

Recent Progress • Approximate. • Similar evolution has happened in other fields: – fluid and heavy-traffic approximation in queueing networks – approximation algorithms in CS theory • Approximation should be good in engineering-relevant regimes.

Two Regimes • Interference-limited regime: – noise is small compared to signals. – focuses on interactions between signals rather than the stochastic noise • Large-network regime: – networks with large number of nodes – focuses on macroscopic scaling laws

Overview • Lecture 1: interference channels – 2 -user interference channel capacity to within 1 bit/s/Hz – Deeper insight via a deterministic channel model – Generalization to some many-user interference channels. • Lecture 2: relay networks – relay channel capacity to within 1 bit/s/Hz – single-source-single-destination relay network capacity to within constant gap

Overview • Lecture 3: Large networks – Networks with many source-destination pairs – Information theoretic optimal scaling laws and architectures

Lecture 1: Interference Channels

Interference • Interference management is an central problem in wireless system design. • Within same system (eg. adjacent cells in a cellular system) or across different systems (eg. multiple Wi. Fi networks) • Two basic approaches: – orthogonalize into different bands – full sharing of spectrum but treating interference as noise • What does information theory have to say about the optimal thing to do?

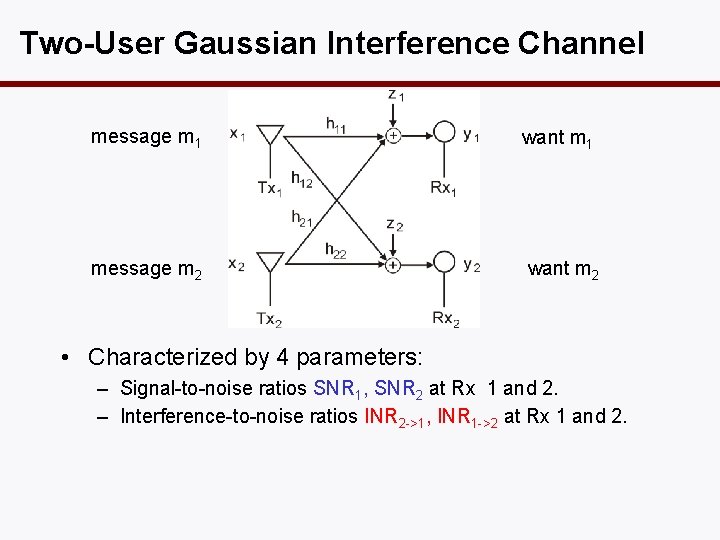
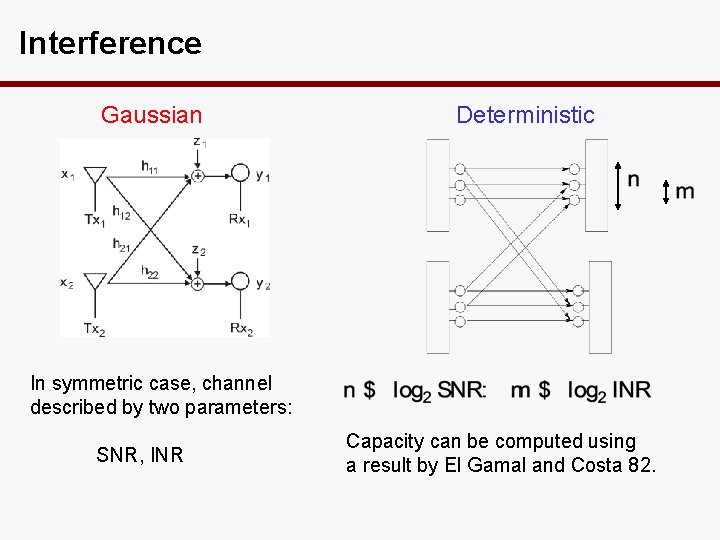
Two-User Gaussian Interference Channel message m 1 want m 1 message m 2 want m 2 • Characterized by 4 parameters: – Signal-to-noise ratios SNR 1, SNR 2 at Rx 1 and 2. – Interference-to-noise ratios INR 2 ->1, INR 1 ->2 at Rx 1 and 2.

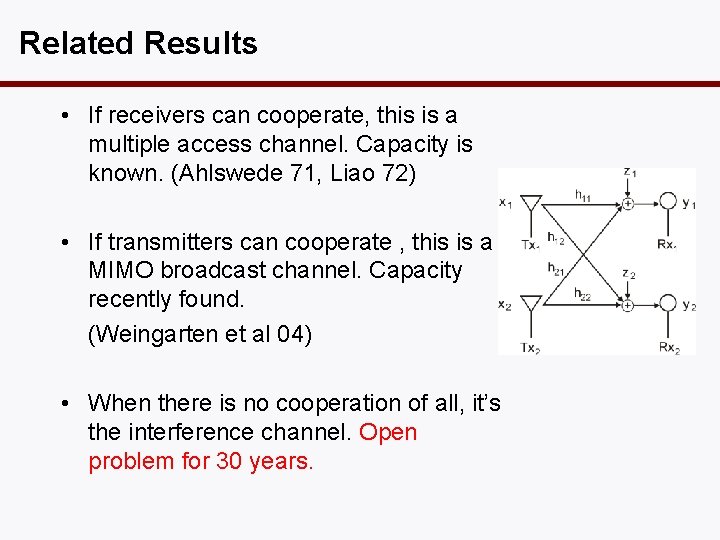
Related Results • If receivers can cooperate, this is a multiple access channel. Capacity is known. (Ahlswede 71, Liao 72) • If transmitters can cooperate , this is a MIMO broadcast channel. Capacity recently found. (Weingarten et al 04) • When there is no cooperation of all, it’s the interference channel. Open problem for 30 years.

State-of-the-Art in 2006 • If INR 1 ->2 > SNR 1 and INR 2 ->1 > SNR 2, then capacity region Cint is known (strong interference, Han. Kobayashi 1981, Sato 81) • Capacity is unknown for any other parameter ranges. • Best known achievable region is due to Han. Kobayashi (1981). • Hard to compute explicitly. • Unclear if it is optimal or even how far from capacity. • Some outer bounds exist but unclear how tight (Sato 78, Costa 85, Kramer 04).

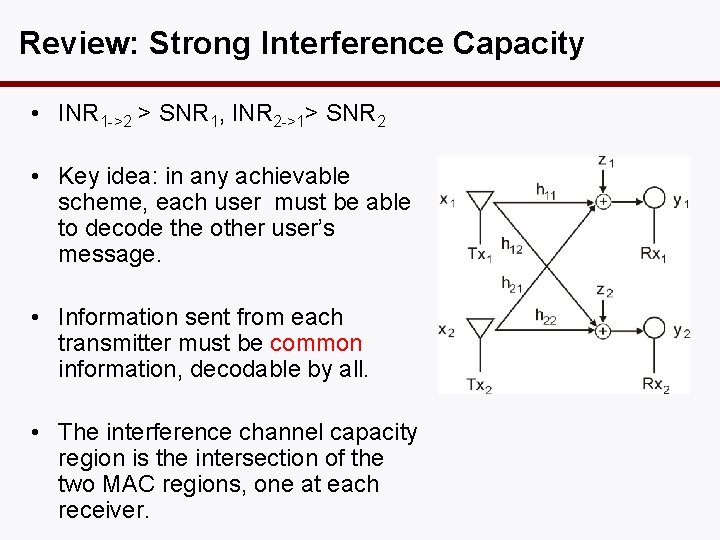
Review: Strong Interference Capacity • INR 1 ->2 > SNR 1, INR 2 ->1> SNR 2 • Key idea: in any achievable scheme, each user must be able to decode the other user’s message. • Information sent from each transmitter must be common information, decodable by all. • The interference channel capacity region is the intersection of the two MAC regions, one at each receiver.

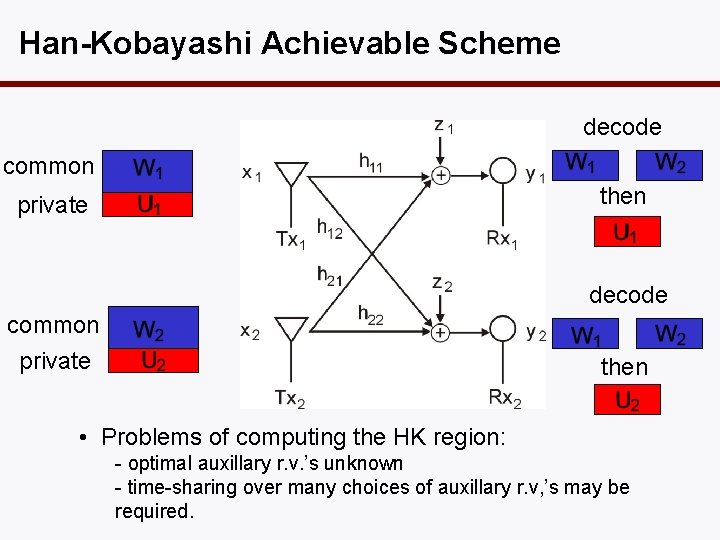
Han-Kobayashi Achievable Scheme decode common then private decode common private then • Problems of computing the HK region: - optimal auxillary r. v. ’s unknown - time-sharing over many choices of auxillary r. v, ’s may be required.

Interference-Limited Regime • At low SNR, links are noise-limited and interference plays little role. • At high SNR and high INR, links are interferencelimited and interference plays a central role. • Classical measure of performance in the high SNR regime is the degree of freedom.

Baselines (Symmetric Channel) • Point-to-point capacity: • Achievable rate by orthogonalizing: • Achievable rate by treating interference as noise:

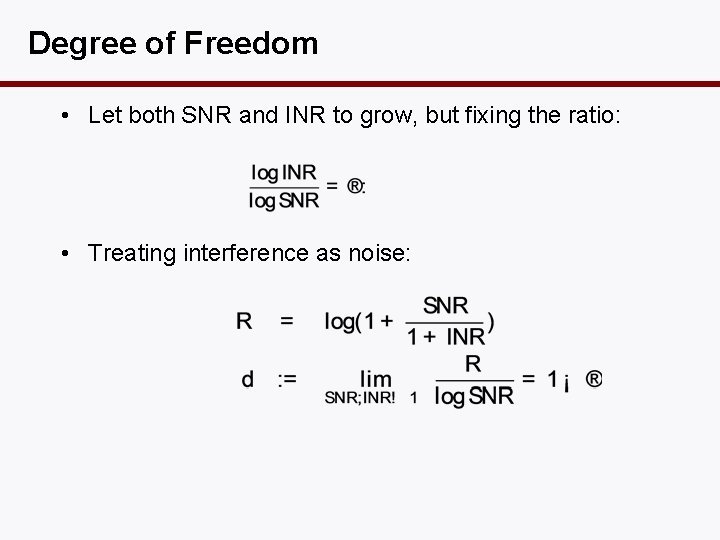
Degree of Freedom • Let both SNR and INR to grow, but fixing the ratio: • Treating interference as noise:

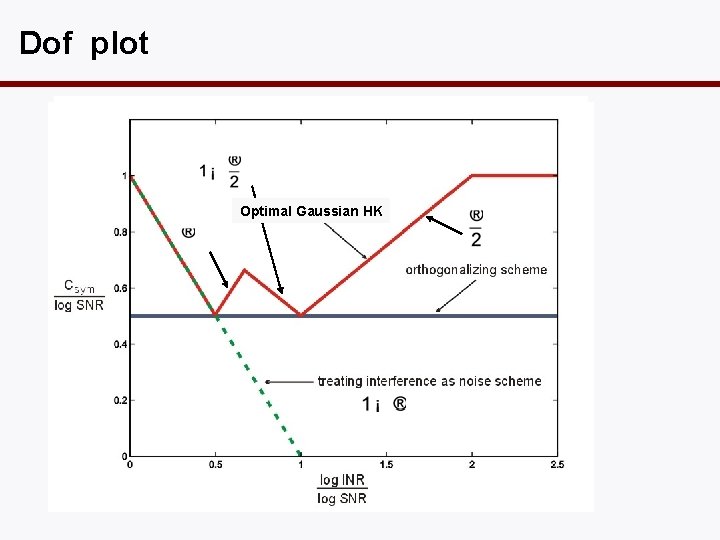
Dof plot Optimal Gaussian HK

Dof-Optimal Han-Kobayashi • Only a single split: no time-sharing. • Private power set so that interference is received at noise level at the other receiver.

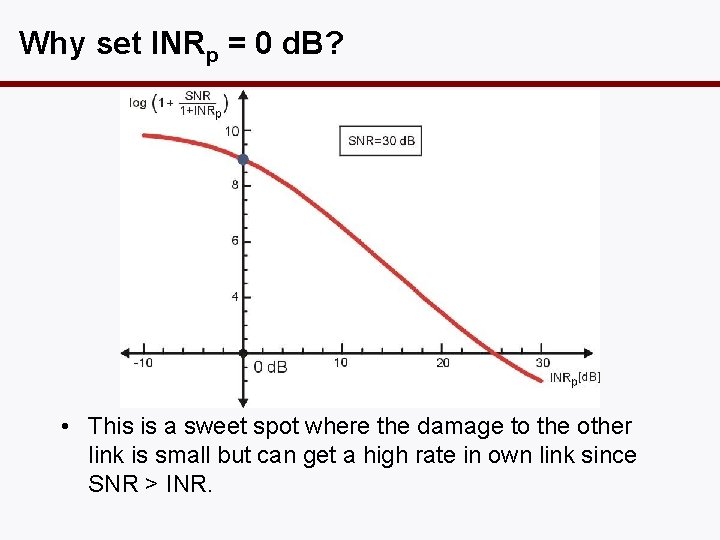
Why set INRp = 0 d. B? • This is a sweet spot where the damage to the other link is small but can get a high rate in own link since SNR > INR.

Can we do Better? • We identified the Gaussian HK scheme that achieves optimal dof. • But can one do better by using non-Gaussian inputs or a scheme other than HK? • Answer turns out to be no. • The dof achieved by the simple HK scheme is the dof of the interference channel. • To prove this, we need outer bounds.

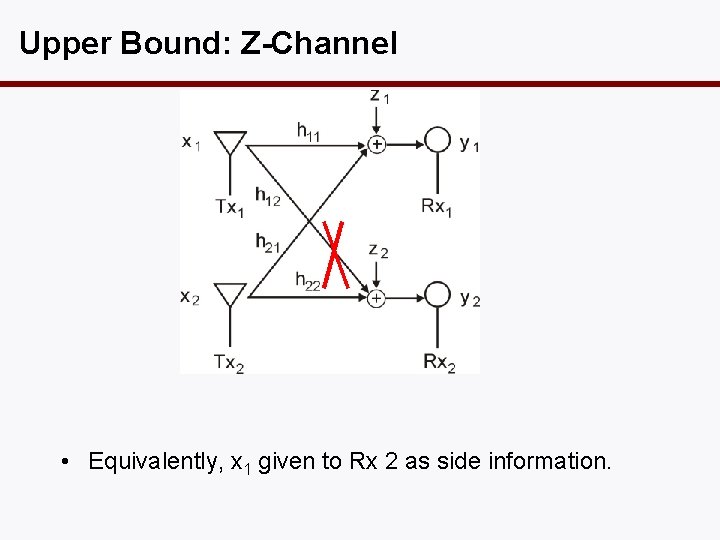
Upper Bound: Z-Channel • Equivalently, x 1 given to Rx 2 as side information.

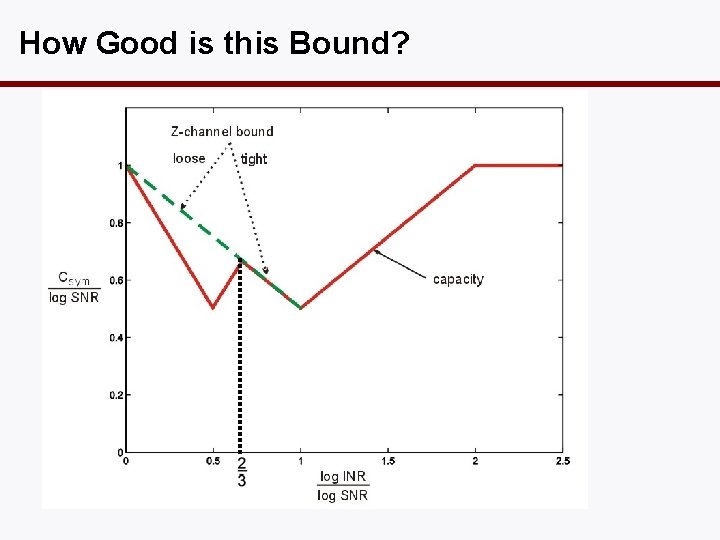
How Good is this Bound?

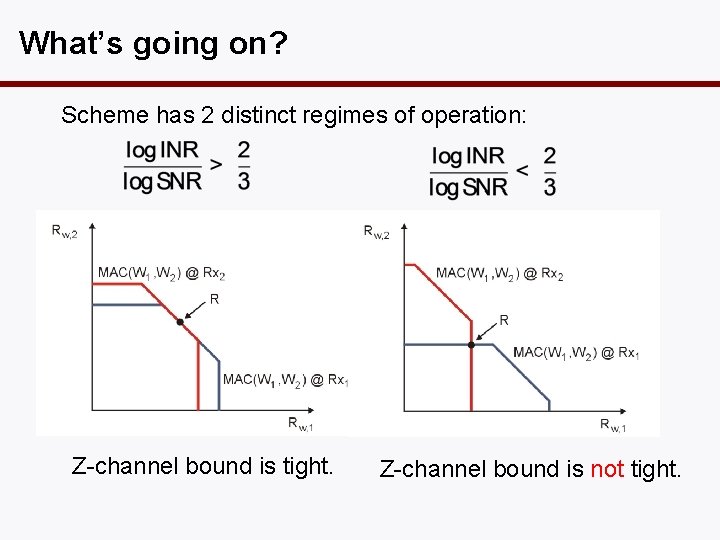
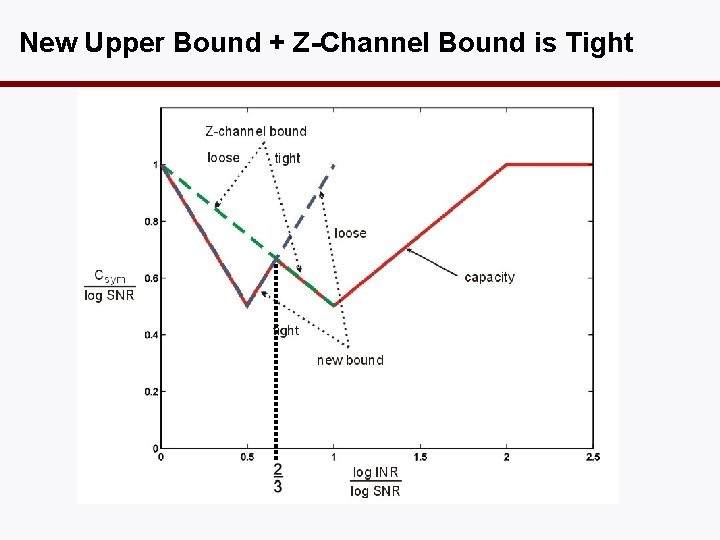
What’s going on? Scheme has 2 distinct regimes of operation: Z-channel bound is tight. Z-channel bound is not tight.

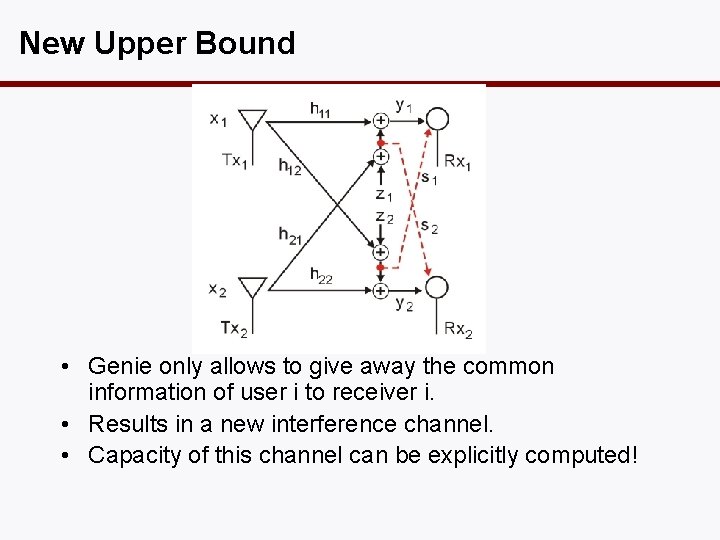
New Upper Bound • Genie only allows to give away the common information of user i to receiver i. • Results in a new interference channel. • Capacity of this channel can be explicitly computed!

New Upper Bound + Z-Channel Bound is Tight

Back from Infinity In fact, the simple HK scheme can achieve within 1 bit/s/Hz of capacity for all values of channel parameters: For any rates in Cint, this scheme can achieve (Etkin, T. & Wang 06)

From 1 -Bit to 0 -Bit The new upper bound can further be sharpened to get exact results in the low-interference regime ( < 1/3). (Shang, Kramer, Chen 07, Annaprueddy & Veeravalli 08, Motahari&Khandani 07)

From Low-Noise to No-Noise • The 1 -bit result was obtained by first analyzing the dof of the Gaussian interference channel in the lownoise regime. • Turns out there is a deterministic interference channel which captures exactly the behavior of the interference-limited Gaussian channel. • Identifying this underlying deterministic structure allows us to generalize the approach.

Point-to-Point Gaussian Deterministic Transmit a real number Least significant bits are truncated at noise level. If we have n / SNR on the d. B scale

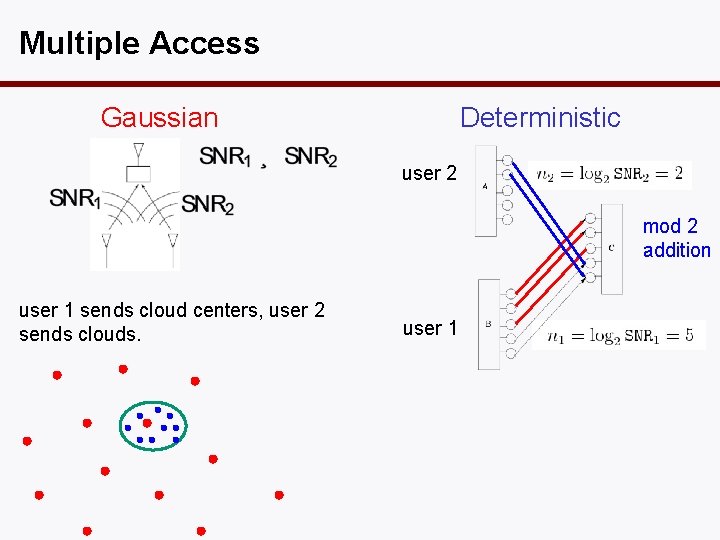
Multiple Access Gaussian Deterministic user 2 mod 2 addition user 1 sends cloud centers, user 2 sends clouds. user 1

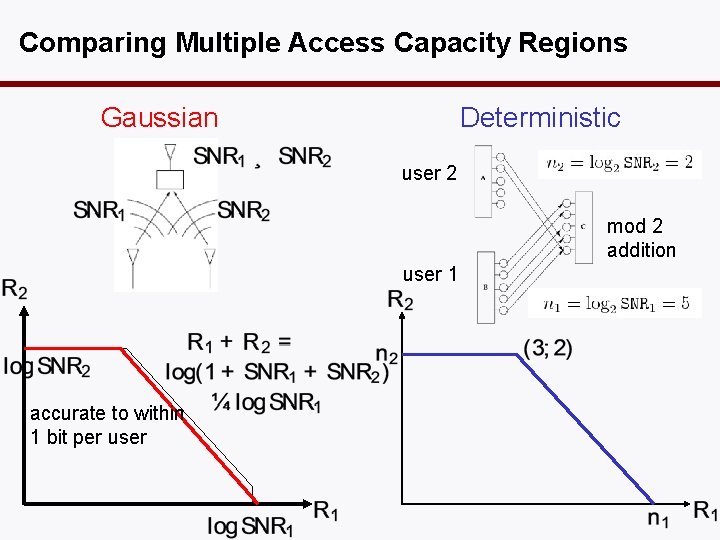
Comparing Multiple Access Capacity Regions Gaussian Deterministic user 2 mod 2 addition user 1 accurate to within 1 bit per user

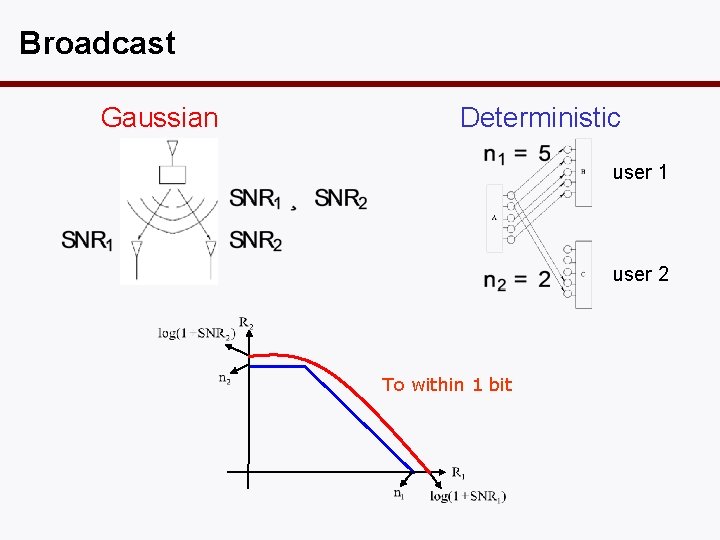
Broadcast Gaussian Deterministic user 1 user 2 To within 1 bit

Interference Gaussian Deterministic In symmetric case, channel described by two parameters: SNR, INR Capacity can be computed using a result by El Gamal and Costa 82.

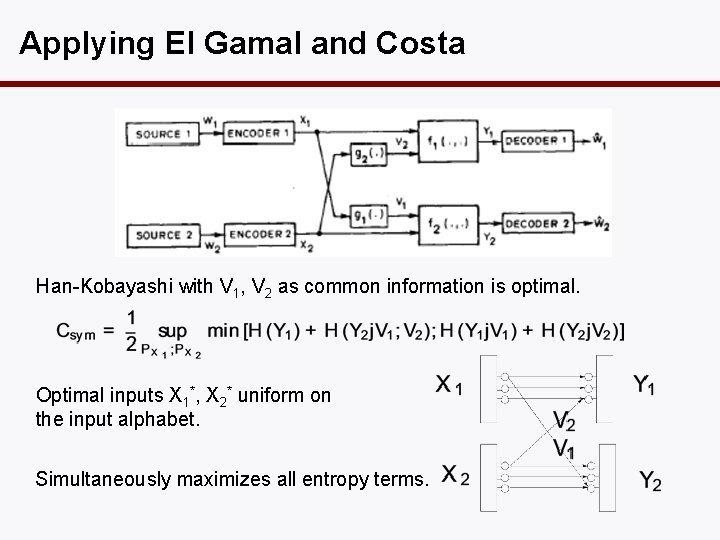
Applying El Gamal and Costa Han-Kobayashi with V 1, V 2 as common information is optimal. Optimal inputs X 1*, X 2* uniform on the input alphabet. Simultaneously maximizes all entropy terms.

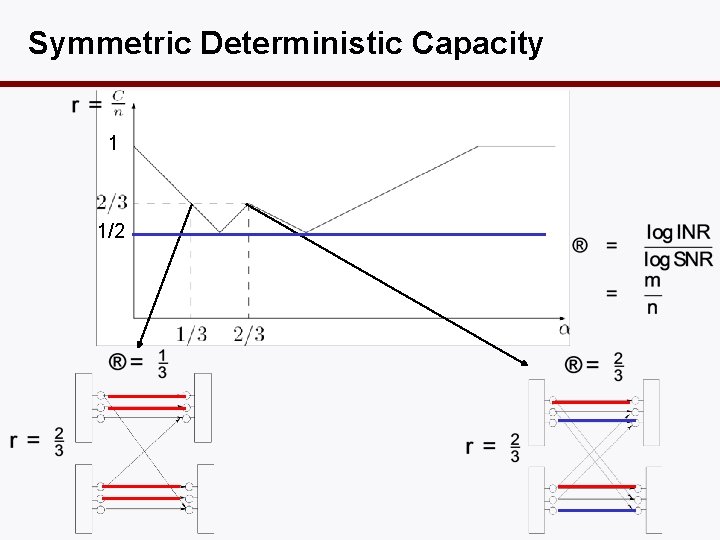
Symmetric Deterministic Capacity 1 1/2

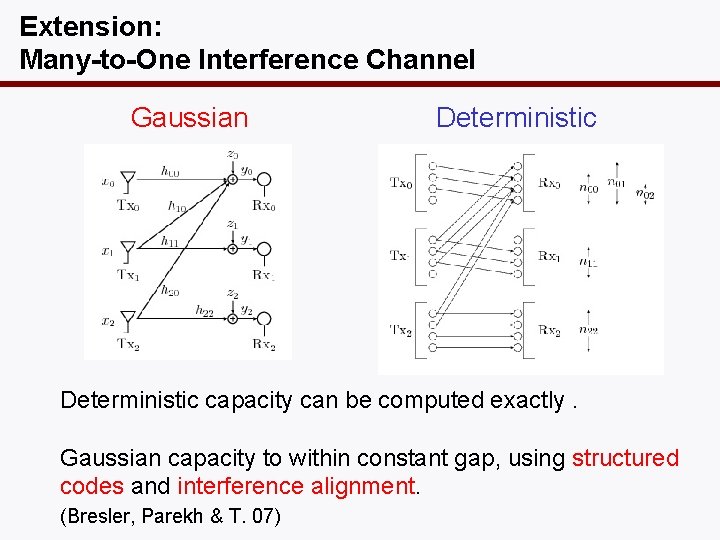
Extension: Many-to-One Interference Channel Gaussian Deterministic capacity can be computed exactly. Gaussian capacity to within constant gap, using structured codes and interference alignment. (Bresler, Parekh & T. 07)

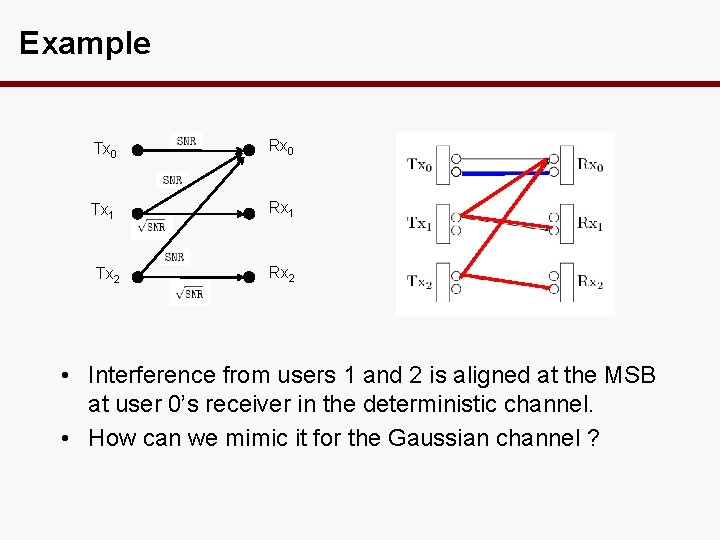
Example Tx 0 Rx 0 Tx 1 Rx 1 Tx 2 Rx 2 • Interference from users 1 and 2 is aligned at the MSB at user 0’s receiver in the deterministic channel. • How can we mimic it for the Gaussian channel ?

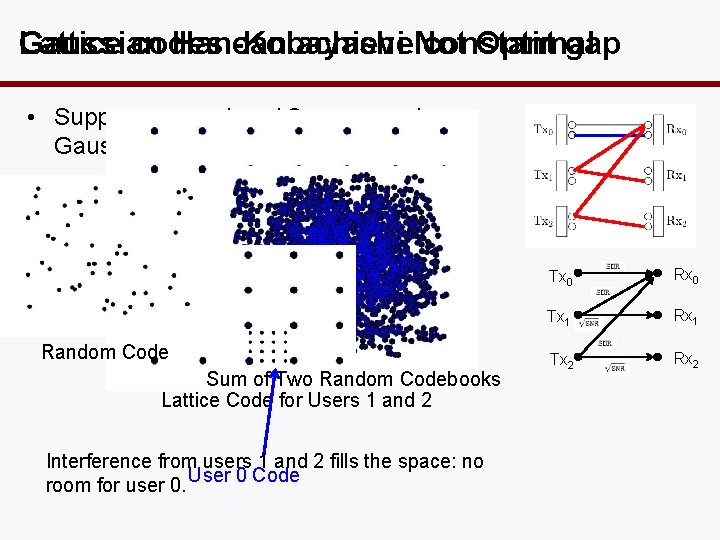
Gaussian Lattice codes Han-Kobayashi can achieve. Not constant Optimal gap • Suppose users 1 and 2 use a random Gaussian codebook: Random Code Sum of Two Random Codebooks Lattice Code for Users 1 and 2 Interference from users 1 and 2 fills the space: no room for user 0. User 0 Code Tx 0 Rx 0 Tx 1 Rx 1 Tx 2 Rx 2

Interference Channels: Recap • In two-user case, we showed that an existing strategy can achieve within 1 bit to optimality. • In many-to-one case, we showed that a new strategy can do much better. • General K-user interference channel still open.

Lecture 2: Relay Networks

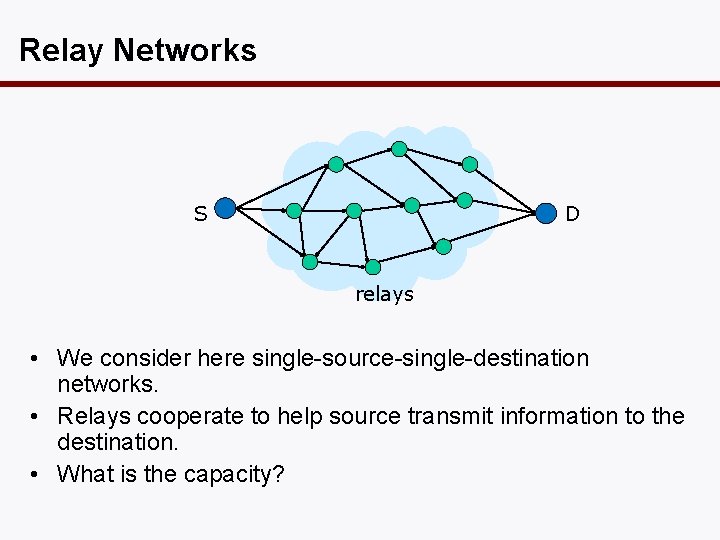
Relay Networks D S relays • We consider here single-source-single-destination networks. • Relays cooperate to help source transmit information to the destination. • What is the capacity?

History • The (single) relay channel was first proposed by Van der Meulen in 1971. • Cover and El Gamal (1979) provided a whole array of achievable strategies: – decode-and-forward – Partial-decode-and-forward – Compress-and-forward • Recent generalization of these techniques to more than 1 relay (Gupta & Kumar, Xie & Kumar, Kramer, Gastpar and Gupta). • Performance of these schemes on general networks not easily characterizable.

Approach • General upper bound: cutset bound. • Are any of these schemes within a constant gap of optimality for general networks? • If not, find a scheme which is. • We approach the problem via the deterministic model. (Avestimehr, Diggavi & T. 07)

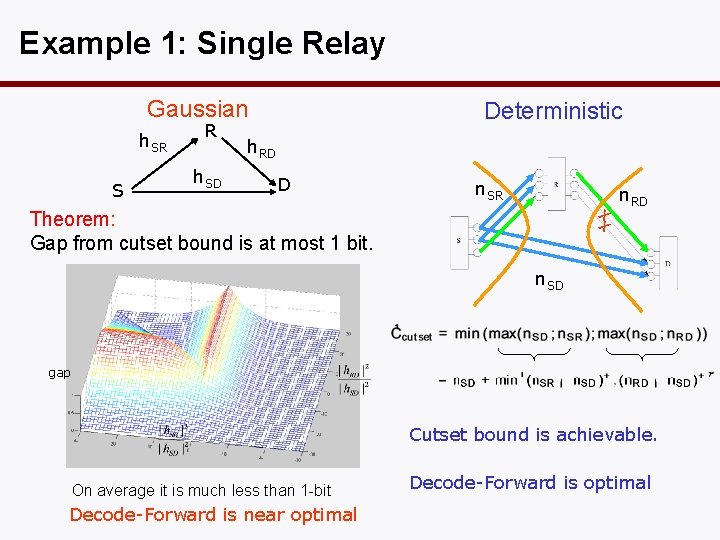
Example 1: Single Relay Gaussian h. SR S R h. SD Deterministic h. RD D n. SR x x Theorem: Gap from cutset bound is at most 1 bit. n. RD n. SD gap Cutset bound is achievable. On average it is much less than 1 -bit Decode-Forward is near optimal Decode-Forward is optimal

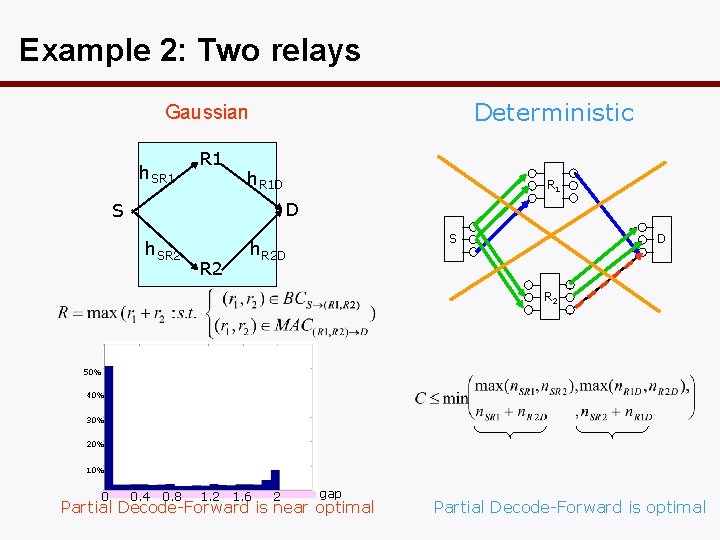
Example 2: Two relays Deterministic Gaussian h. SR 1 h. R 1 D R 1 D S h. SR 2 S h. R 2 D D R 2 50% 40% 30% 20% 10% 0 0. 4 0. 8 1. 2 1. 6 2 gap Partial Decode-Forward is near optimal Partial Decode-Forward is optimal

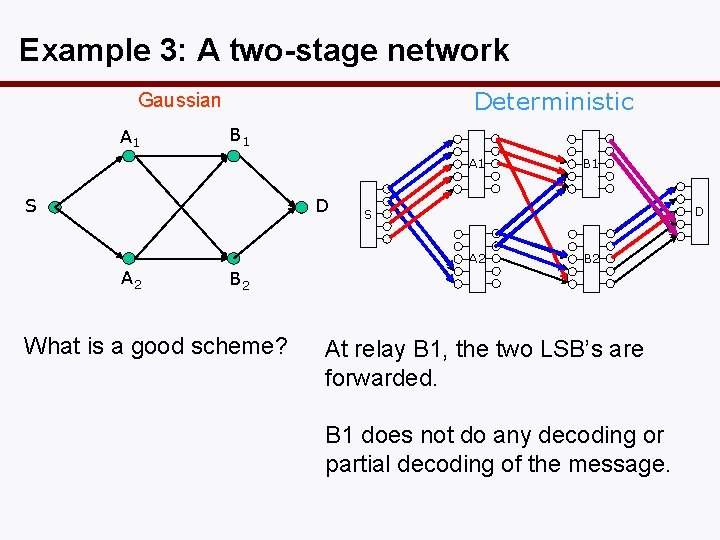
Example 3: A two-stage network Deterministic Gaussian A 1 B 1 A 1 S D D S A 2 B 1 B 2 What is a good scheme? At relay B 1, the two LSB’s are forwarded. B 1 does not do any decoding or partial decoding of the message.

Questions • Is the cutset bound always achieved on arbitrary networks for the deterministic model? • What is the structure of the capacity-achieving strategy? • Can we mimic that to find an approximately optimal strategy for general Gaussian networks?

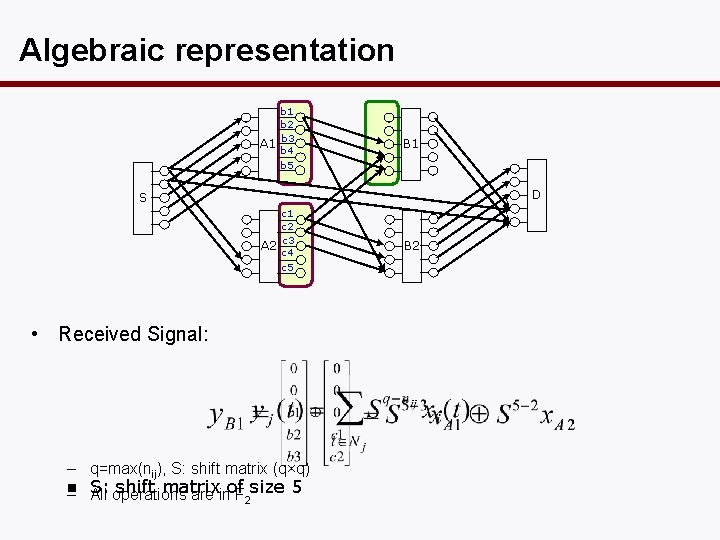
Algebraic representation A 1 b 2 b 3 b 4 b 5 B 1 D S A 2 c 1 c 2 c 3 c 4 c 5 • Received Signal: – q=max(nij), S: shift matrix (q×q) n shift matrix – S: All operations are inof F 2 size 5 B 2

General linear finite-field model • Channel from i to j is described by an arbitrary channel matrix Gij operating on • Received signal: (mod 2) – Deterministic model: – Wireline network also a special case

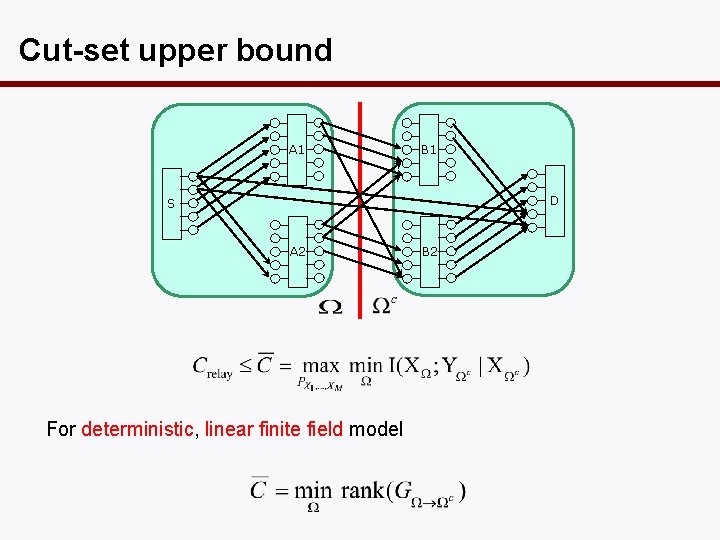
Cut-set upper bound A 1 B 1 D S A 2 For deterministic, linear finite field model B 2

Achievability of Cutset Bound Theorem: Cutset bound is achievable, Ø In wireline networks, the capacity of links from W to Wc is just summation of Ø This theorem is a generalization of Ford-Fulkerson maxflow min-cut theorem Ø Also holds in the multicast scenario Ø Generalization of network coding to achieve the multicast capacity of wireline networks (Ahlswede-Cai-Li-Yeung)

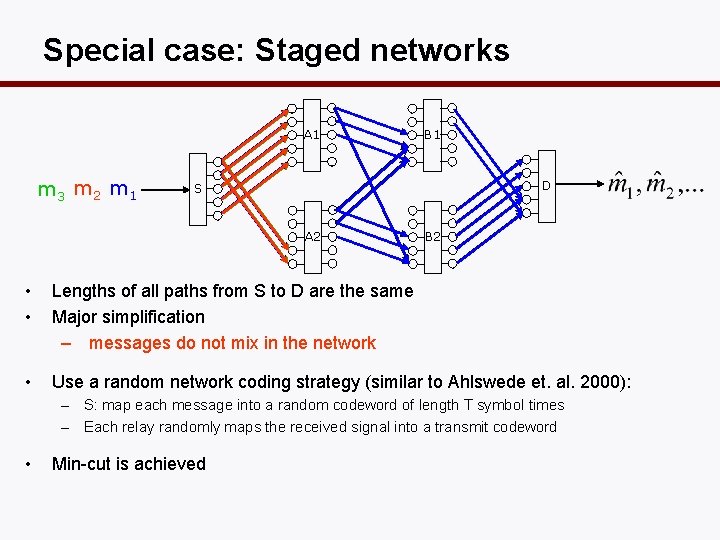
Special case: Staged networks A 1 m 3 m 2 m 1 B 1 D S A 2 B 2 • • Lengths of all paths from S to D are the same Major simplification – messages do not mix in the network • Use a random network coding strategy (similar to Ahlswede et. al. 2000): – S: map each message into a random codeword of length T symbol times – Each relay randomly maps the received signal into a transmit codeword • Min-cut is achieved

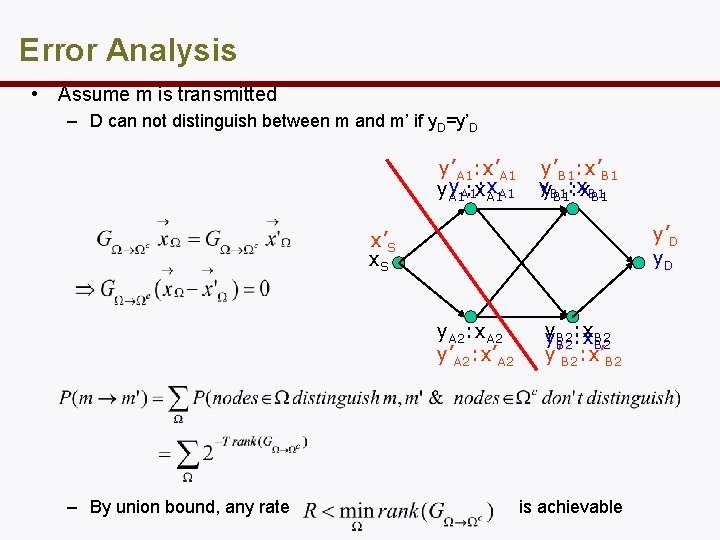
Error Analysis • Assume m is transmitted – D can not distinguish between m and m’ if y. D=y’D y’A 1: x’A 1 y. A 1 : x: x A 1 A 1 y’B 1: x’B 1 yy. B 1 : x B 1: x. B 1 y’D y. D x’S x. S y. A 2: x. A 2 y’A 2: x’A 2 – By union bound, any rate y : x. B 2 y. B 2: x. B 2 y’B 2: x’B 2 is achievable

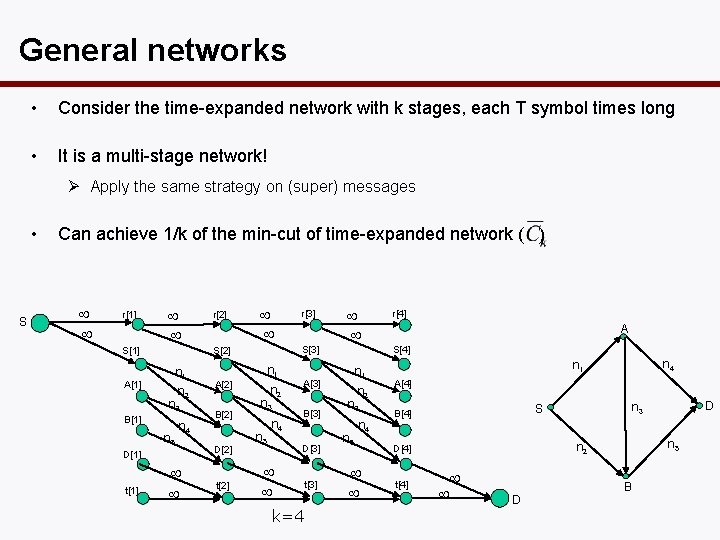
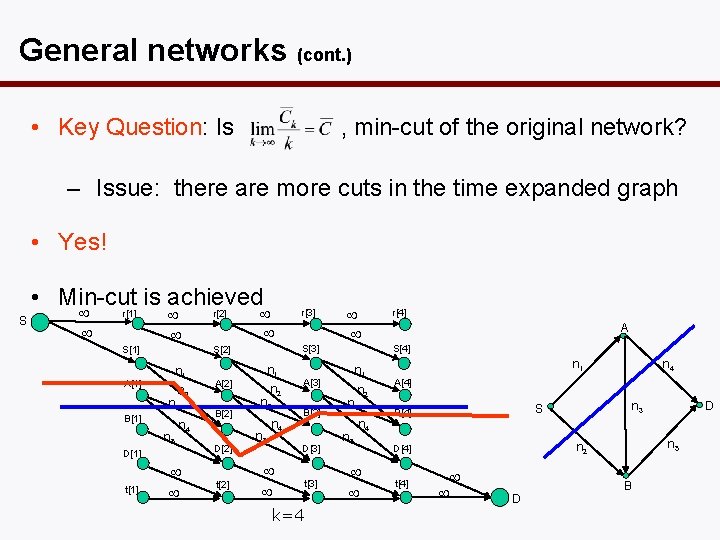
General networks • Consider the time-expanded network with k stages, each T symbol times long • It is a multi-stage network! Ø Apply the same strategy on (super) messages • S Can achieve 1/k of the min-cut of time-expanded network ( ) r[1] S[1] n 1 n 2 n 3 B[1] n 5 t[1] n 4 n 1 A[2] B[2] D[2] t[2] r[3] S[2] A[1] D[1] r[2] n 2 n 3 n 5 n 4 A[3] B[3] D[3] t[3] k=4 n 1 n 2 n 3 n 5 n 4 r[4] A S[4] n 4 n 1 A[4] D D n 5 n 2 D[4] t[4] n 3 S B[4] B

General networks (cont. ) • Key Question: Is , min-cut of the original network? – Issue: there are more cuts in the time expanded graph • Yes! S • Min-cut is achieved r[1] r[2] S[1] A[1] n 2 n 3 B[1] n 5 D[1] t[1] S[3] S[2] n 1 n 4 n 1 A[2] B[2] D[2] t[2] r[3] n 2 n 3 n 5 n 4 A[3] B[3] D[3] t[3] k=4 n 1 n 2 n 3 n 5 n 4 r[4] A S[4] n 4 n 1 A[4] D D n 5 n 2 D[4] t[4] n 3 S B[4] B

Proof • Cut value is: • Lower bound cut value by sum of k cut-values of original network. • Theorem: , m=1…k ={nodes that appear at least m times in Ri’s} • S Proof: Based on Submodularity of entropy function r[1] r[2] r[3] r[4] S[1] S[2] S[3] S[4] A[1] A[2] A[3] A[4] A 3 S B[1] B[2] B[3] B[4] D[1] D[2] D[3] D[4] t[1] t[2] t[3] t[4] 4 1 5 2 D D B

Back to Gaussian Networks Deterministic p p p S encodes the message over T • symbol times Each relay randomly maps the • received signal into a transmit codeword D decodes the message deterministically • optimal Gaussian S encodes the message over T symbol times Each relay, – Quantizes the received signal at noise level – Randomly maps it into a Gaussian codeword D decodes the message by finding the one that is jointly typical with y. D approx. optimal

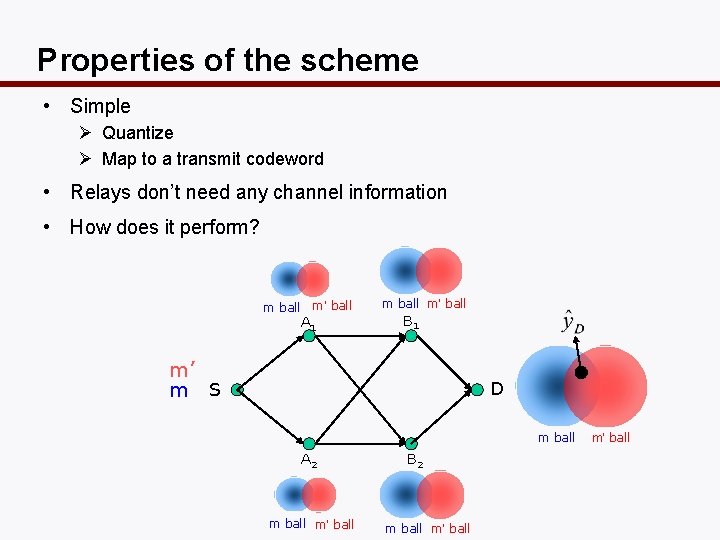
Properties of the scheme • Simple Ø Quantize Ø Map to a transmit codeword • Relays don’t need any channel information • How does it perform? m ball m’ ball A 1 m ball m’ ball B 1 m’ m S D m ball A 2 m ball m’ ball B 2 m ball m’ ball

Approximate Capacity of Gaussian Networks • Theorem: for any Gaussian relay network - is the cut-set upper bound on the capacity is a constant that depends on size of the network, but not the channel gains or SNR’s of the links - Uniform approximation of the capacity for all values of channel gains.

Earlier Work on Deterministic Relay Networks • Single-relay semi-deterministic channel (El Gamal & Aref 79) • Aref’s relay network with general deterministic broadcast but no interference (Aref 80, Ratnakar & Kramer 06) • But connection to Gaussian networks missing.