Information Theory for Mobile AdHoc Networks ITMANET The

Information Theory for Mobile Ad-Hoc Networks (ITMANET): The FLo. WS Project A Distributed Newton Method for Network Optimization Ali Jadbabaie and Asu Ozdaglar

A Distributed Newton Method for Network Optimization (Jadbabaie, Ozdaglar) MAIN ACHIEVEMENT: • We developed a Newton method that solves network Most existing distributed optimization methods rely on dual decomposition and subgradient (first order) algorithms optimization problems in a distributed manner. • We provide convergence and rate of convergence guarantees for the proposed method. • Simulation experiments on a series of randomly generated graphs suggest superiority of the distributed Newton method over dual subgradient methods. IMPACT STATUS QUO ACHIEVEMENT DESCRIPTION • These algorithms easy to distribute • However, they can be quite slow to converge limiting their use in rapidly changing dynamic wireless networks NEW INSIGHTS HOW IT WORKS: • Constrained Newton method Combine Newton (second order) methods with consensus policies to distribute the computations associated with the dual Newton step • Dual Newton step found by solving a discrete Poisson equation involving the graph Laplacian. • Using a consensus-based local averaging scheme, this can be done using only local information. ASSUMPTIONS AND LIMITATIONS: • Solves minimum cost network flow problems • Dual and primal steps computed separately NEXT-PHASE GOALS Significant improvements with the distributed Newton method compared to subgradient methods Second order methods for distributed network optimization • Understand the impact of network structure (connectivity and mobility) on algorithm performance • Design algorithms that compute primal and dual steps jointly • Extend second order methods to network utility maximization Distributed Second Order Methods with Convergence Guarantees

Motivation • Increasing interest in distributed optimization and control of ad hoc wireless networks, which are characterized by: – Lack of centralized control and access to information – Time-varying connectivity • Control-optimization algorithms deployed in such networks should be: – Distributed relying on local information – Robust against changes in the network topology • Standard Approach to Distributed Optimization in Networks: – Use dual decomposition and subgradient (or first-order) methods – Yields distributed algorithms for some classes of problems – Suffers from slow rate of convergence properties

This Work • We propose a new Newton-type (second-order) method, which is distributed and achieves superlinear convergence rate – Relies on representing the dual Newton direction as the solution of a discrete Poisson equation involving the graph Laplacian – Consensus-type iterative schemes used to compute the Newton direction and the stepsize with some error – We show that the proposed method converges superlinearly to an error neighborhood – Simulation results demonstrate the superior performance of our method compared to subgradient schemes

Minimum Cost Network Optimization Problem b 1 • Consider a network represented by a directed graph • Each edge has a convex cost function as a function of the flow on edge e • We denote the demand at node i by bi bn The minimum cost network optimization problem is given by: where A is the node-edge incidence matrix of the graph.

Newton Method • Let • Given an initial primal vector x 0, the iterates are generated by where vk is the Newton step given as the solution to the following system of linear equations: • The dual Newton step wk is given by where Hk is the Hessian matrix. • This computation requires global information.

Distributed Computation of the Dual Step • The key step in developing a decentralized iterative scheme for the computation of the vector wk is to recognize that the matrix is the weighted Laplacian of the underlying graph • Hence the computation of dual Newton step can be written as where • The preceding equation can be solved iteratively as: For all (dependence on k suppressed for convenience). • This iteration relies only on local information

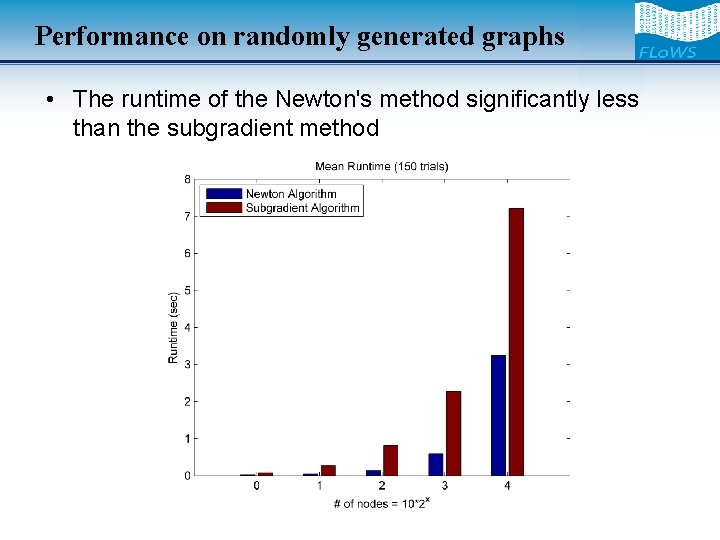
Performance on randomly generated graphs • The runtime of the Newton's method significantly less than the subgradient method

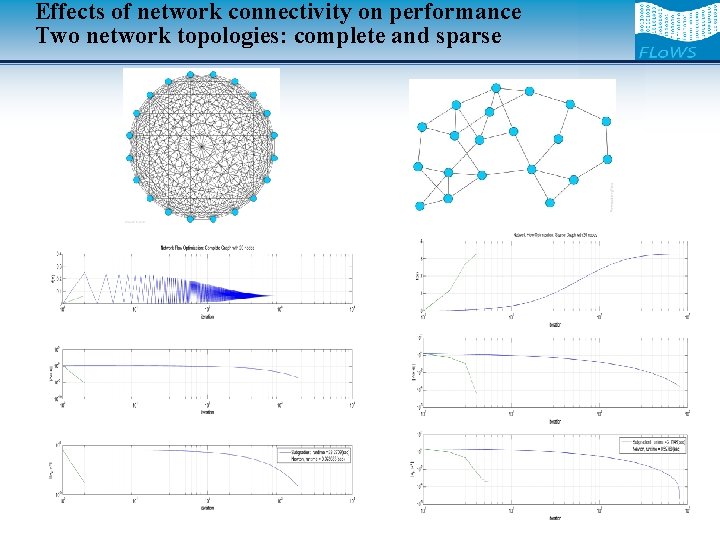
Effects of network connectivity on performance Two network topologies: complete and sparse

Conclusions • We presented a distributed Newton-type method for minimum cost network optimization problem • We used consensus schemes to compute the dual Newton direction and the stepsize in a distributed manner • We showed that even in the presence of errors, the proposed method converges superlinearly to an error neighborhood • Future Work: – Understand the impact of network structure (connectivity and mobility) on algorithm performance – Ongoing work extends this idea to Network Utility Maximization • Papers: – Jadbabaie and Ozdaglar, “A Distributed Newton Method for Network Optimization, ” submitted for publication in CDC 2009.