Information Theoretic Measures for Clusterings Comparison Is a

Information Theoretic Measures for Clusterings Comparison: Is a Correction for Chance Necessary? Nguyen Xuan Vinh, UNSW Julien Epps, UNSW James Bailey, Uni Melbourne Australia's ICT Research Centre of Excellence 14 -17 June 2009 ICML’ 09 p. 1/28

Correction for Chance for Information Theoretic based measures - Outline 1. Introduction to clustering and clustering comparison 2. A brief survey of clustering comparison measures 3. How chance agreement affects information theoretic based measures? 4. Adjusted-for-chance measures 5. Conclusion 14 -17 June 2009 ICML’ 09 p. 2/28

Introduction Clustering: the “art” of dividing data points in a data set into meaningful groups Notation: • Data set: S={s 1, s 2, . . . s. N} • (Hard) clustering: a way to partition the data set into non-overlapping parts • U={U 1, U 2, . . . UR} Ui's are non-overlapping subsets of S • V={V 1, V 2, . . . VC} Vj's are non-overlapping subsets of S 14 -17 June 2009 ICML’ 09 p. 3/28

Introduction Clustering comparison measures are used to: • Evaluate the goodness of clustering solutions (assuming the “true” clustering is known) • Evaluate clustering algorithms (over multiple data sets) More active use: • To search for a good clustering solution • as in Ensemble clustering • To quantify the discordance within a set of clusterings • => stability assessment • might give useful hint to model selection, such as choosing the “right” number of cluster 14 -17 June 2009 ICML’ 09 p. 4/28

Correction for Chance for Information Theoretic based measures - Outline • Introduction to clustering and clustering comparison • A brief review of Clustering comparison measures • How chance agreement affects Information theoretic based measures? • Adjusted-for-chance measures • Conclusion 14 -17 June 2009 ICML’ 09 p. 5/28

Clustering comparison measures A brief review 3 categories: • Pair-counting based – Rand Index (RI), Adjusted Rand Index (ARI) – Jaccard Index, Folkes & Mallows index … – 22 in total (Albatineh et. al. (2006)) • Set-matching based – The “classification error”, the Van Dongen metric • Information theoretic based – Mutual Information (MI), normalized MI – Variation of Information (Meila (2005)) 14 -17 June 2009 ICML’ 09 p. 6/28

Clustering comparison measures A brief review – Rand Index • Rand Index (RI): a set of N data point has N(N-1)/2 pairs of points, which can be classified into 4 categories • Proportions of pairs that both clusterings agree 14 -17 June 2009 ICML’ 09 p. 7/28

Clustering comparison measures A brief review – Adjusted Rand Index • Problem with the Rand Index: baseline value (average value between random clusterings) is high and varies • Solution: Adjusted index • Adjusted Rand Index 14 -17 June 2009 ICML’ 09 p. 8/28

Why do we care about Information theoretic based measures? • Strong theoretical foundation: information theory • Ability to detect general non-linear correlation • As a matter of fact, they are receiving increasing interest • Ensemble clustering: Strehl and Ghosh (2002), (Fern and Brodley (2003); Singh et al. (2007); He et al. (2008); • Comparison measures: Meila (2003, 2005, 2007), Vinh and Phuong (2008 a, 2008 b) 14 -17 June 2009 ICML’ 09 p. 9/28

Ingredients for Information theoretic based measures • Given a clustering U={U 1, U 2, . . . UR} • Entropy of U: • Where: • The uncertainty in determining the cluster label of a datapoint in S 14 -17 June 2009 ICML’ 09 p. 10/28

Ingredients for Information theoretic based measures Mutual information Given the clusterings U={U 1, U 2, . . . UR} V={V 1, V 2, . . . VC} with points distributions P(i)=|Ui|/N P’(j)=|Vj|/N Mutual information is calculated from the Joint distribution of points into clusters in U & V Where: 14 -17 June 2009 ICML’ 09 p. 11/28

Information theoretic based measures • Mutual information – A similarity measure, range: [0, log N] – Measures the information shared between two clusterings • Normalized Mutual Information – Range: [0, 1] • Variation of Information (Meila (2005)) VI(U, V)= H(U)+H(V)- 2 I(U, V) – A dissimilarity measure – Is a true metric on the space of the clusterings – Range: [0, log N] 14 -17 June 2009 ICML’ 09 p. 12/28

Correction for Chance for Information Theoretic based measures - Outline • Introduction to clustering and clustering comparison • A brief survey of Clustering comparison measures • How chance agreement affects Information theoretic based measures? • Adjusted-for-chance measures • Conclusion 14 -17 June 2009 ICML’ 09 p. 13/28

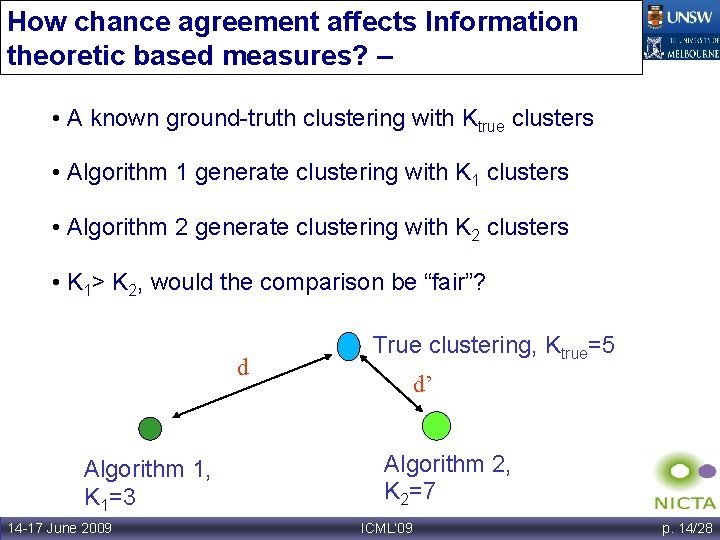
How chance agreement affects Information theoretic based measures? – Scenario 1 • A known ground-truth clustering with Ktrue clusters • Algorithm 1 generate clustering with K 1 clusters • Algorithm 2 generate clustering with K 2 clusters • K 1> K 2, would the comparison be “fair”? d Algorithm 1, K 1=3 14 -17 June 2009 True clustering, Ktrue=5 d’ Algorithm 2, K 2=7 ICML’ 09 p. 14/28

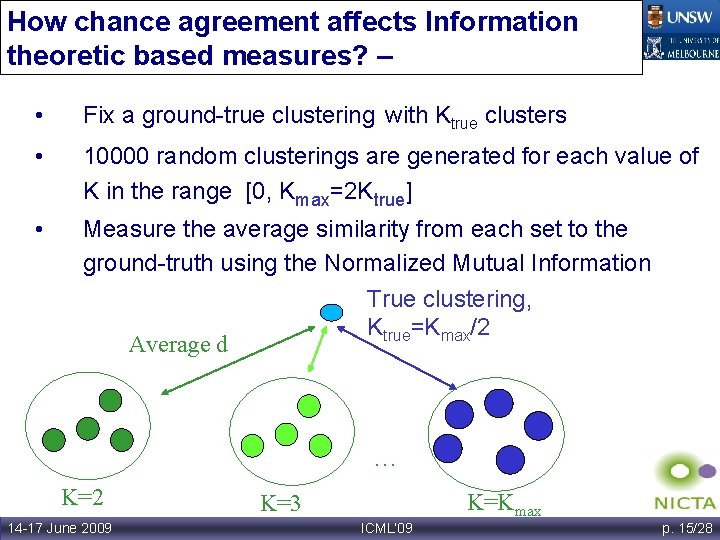
How chance agreement affects Information theoretic based measures? – Experiment 1 • Fix a ground-true clustering with Ktrue clusters • 10000 random clusterings are generated for each value of K in the range [0, Kmax=2 Ktrue] • Measure the average similarity from each set to the ground-truth using the Normalized Mutual Information True clustering, Ktrue=Kmax/2 Average d … K=2 14 -17 June 2009 K=Kmax K=3 ICML’ 09 p. 15/28

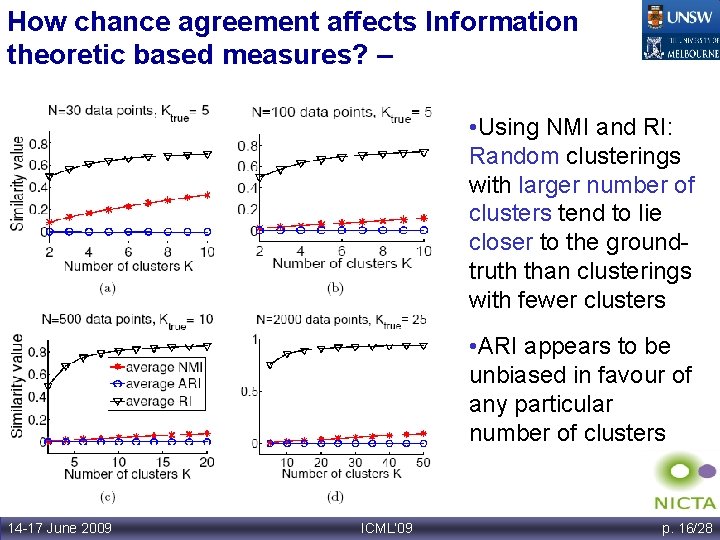
How chance agreement affects Information theoretic based measures? – Experiment 1 • Using NMI and RI: Random clusterings with larger number of clusters tend to lie closer to the groundtruth than clusterings with fewer clusters • ARI appears to be unbiased in favour of any particular number of clusters 14 -17 June 2009 ICML’ 09 p. 16/28

How chance agreement affects Information theoretic based measures? – Scenario 2 Select the appropriate number of clusters • In clustering K is unknown • Approach: – For Hierarchical clustering: 30 stopping rule procedures (Milligan and Cooper (1985)) – For model based clustering: Bayesian Information Criterion (BIC) – The Gap statistics –… – The stability assessment approach 14 -17 June 2009 ICML’ 09 p. 17/28

How chance agreement affects Information theoretic based measures? – Scenario 2 Select the appropriate number of clusters via stability assessment • Generate a multiple sets of clusterings, each having the same number of clusters • Measure the concordance within each set by calculating the average pairwise similarity value (Consensus index) • Higher value indicate stability => a hint to select the true number of clusters #clusters=2 14 -17 June 2009 … #clusters=Ktrue … ICML’ 09 #clusters=Kmax p. 18/28

How chance agreement affects Information theoretic based measures? – Experiment 2: • Generate 200 random clusterings of N data points for each value of K in the range [0, Kmax] • Measure the average pairwise similarity within each set using the Normalized Mutual Information 14 -17 June 2009 ICML’ 09 p. 19/28

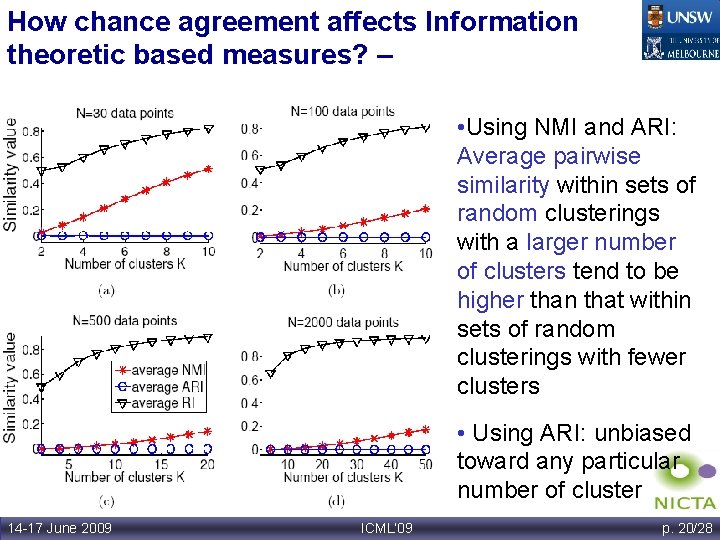
How chance agreement affects Information theoretic based measures? – Experiment 2 • Using NMI and ARI: Average pairwise similarity within sets of random clusterings with a larger number of clusters tend to be higher than that within sets of random clusterings with fewer clusters • Using ARI: unbiased toward any particular number of cluster 14 -17 June 2009 ICML’ 09 p. 20/28

Correction for Chance for Information Theoretic based measures - Outline • Introduction to clustering and clustering comparison • A brief survey of Clustering comparison measures • How chance agreement affects Information theoretic based measures? • Adjusted-for-chance measures • Conclusion 14 -17 June 2009 ICML’ 09 p. 21/28

Adjusting information theoretic measure for chance • Model of Randomness: hypergeometric distribution model (clusterings are created randomly subject to the fixed maginal condition) • Model previously employed for the Adjusted Rand Index. 14 -17 June 2009 ICML’ 09 p. 22/28

Adjusting information theoretic measure for chance • Expected Mutual Information between a pair of random clustering is given by: 14 -17 June 2009 ICML’ 09 p. 23/28

Adjusting Mutual Information (AMI) • General formula for an adjusted similarity measure: • The Adjusted Mutual Information 14 -17 June 2009 ICML’ 09 p. 24/28

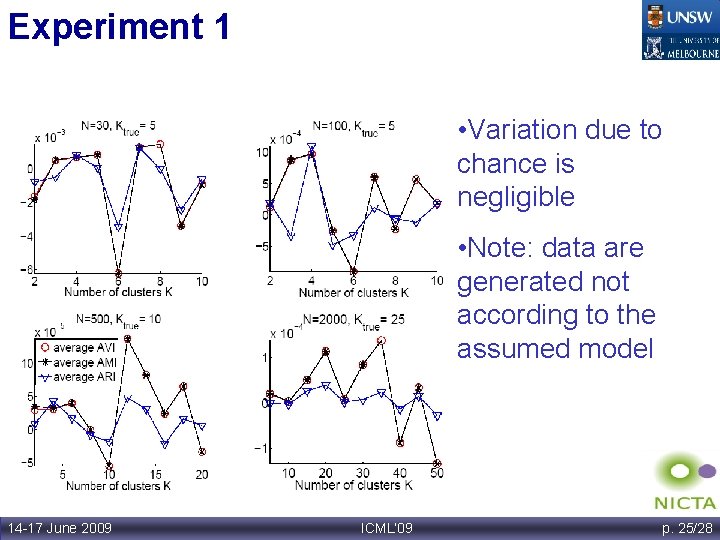
Experiment 1 • Variation due to chance is negligible • Note: data are generated not according to the assumed model 14 -17 June 2009 ICML’ 09 p. 25/28

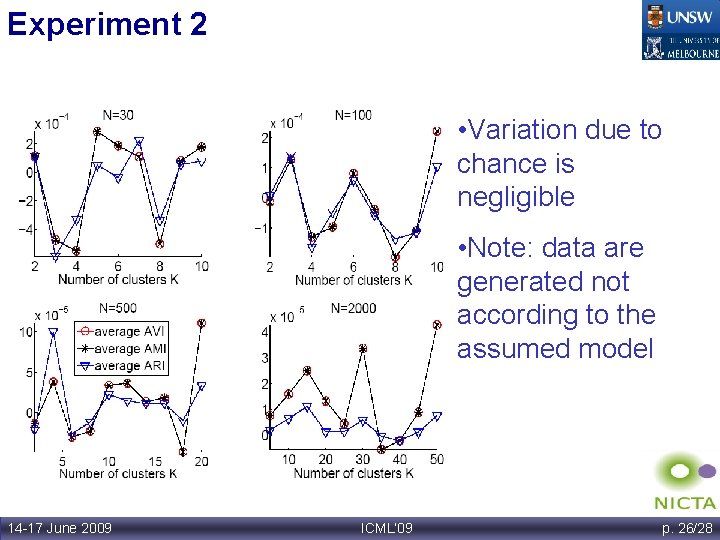
Experiment 2 • Variation due to chance is negligible • Note: data are generated not according to the assumed model 14 -17 June 2009 ICML’ 09 p. 26/28

Conclusion & Future work • Information theoretic measures for clustering comparision are affected by chance, especially when the number of data point is per cluster is small • Adjusted-for-chance measures have been proposed • Work well in practice, despite the hypergemetric assumption of randomness • Code: http: //ee. unsw. edu. au/~nguyenv/Software. htm • What are the differences between the ARI and the AMI? 'Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance', N. X. Vinh, Epps, J. and Bailey, J. , to be submitted. 14 -17 June 2009 ICML’ 09 p. 27/28

Thank you ! 14 -17 June 2009 ICML’ 09 p. 28/28