Information Security Theory vs Reality 0368 4474 01

Information Security – Theory vs. Reality 0368 -4474 -01, Winter 2011 Lecture 14: More on vulnerability and exploits, Fully homomorphic encryption Eran Tromer Slides credit: Vinod Vaikuntanathan (U. Toronto) 1

More on vulnerability exploitation 2

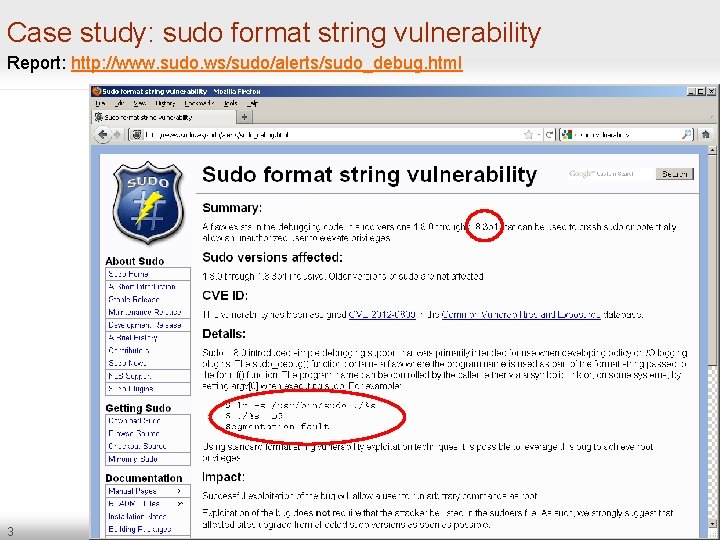
Case study: sudo format string vulnerability Report: http: //www. sudo. ws/sudo/alerts/sudo_debug. html 3

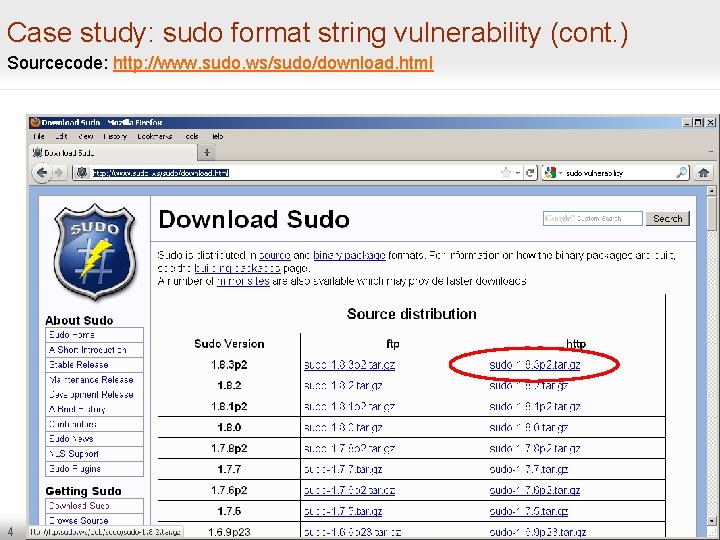
Case study: sudo format string vulnerability (cont. ) Sourcecode: http: //www. sudo. ws/sudo/download. html 4

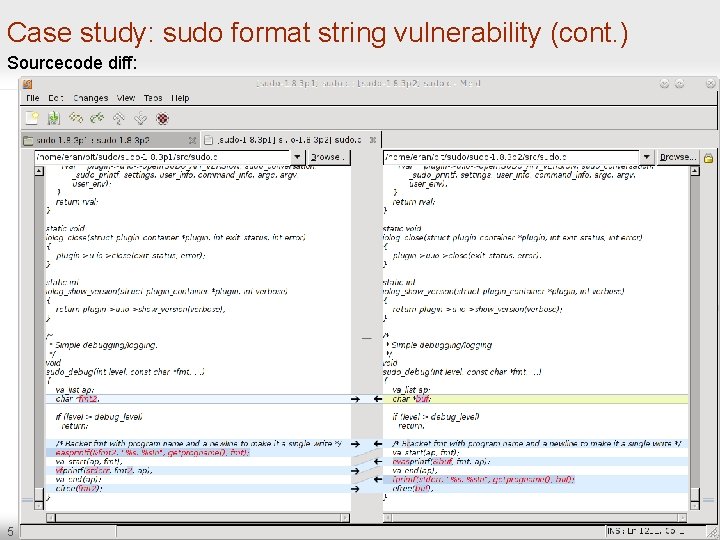
Case study: sudo format string vulnerability (cont. ) Sourcecode diff: 5

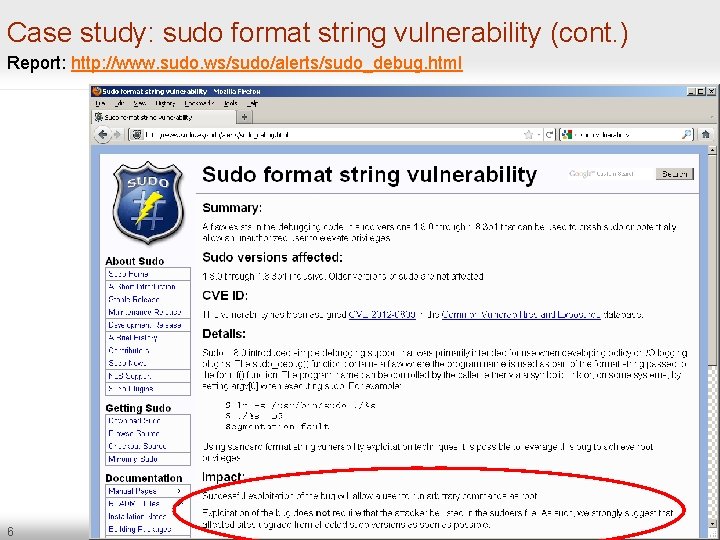
Case study: sudo format string vulnerability (cont. ) Report: http: //www. sudo. ws/sudo/alerts/sudo_debug. html 6

Case study: MS 06 -040 buffer overrun Report: https: //technet. microsoft. com/en-us/security/bulletin/ms 06 -040 7

Case study: MS 06 -040 buffer overrun (cont. ) Report: https: //technet. microsoft. com/en-us/security/bulletin/ms 06 -040 8

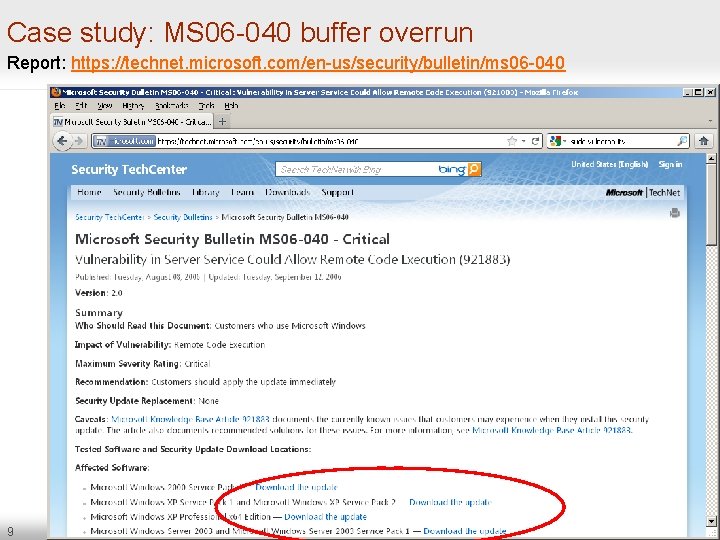
Case study: MS 06 -040 buffer overrun Report: https: //technet. microsoft. com/en-us/security/bulletin/ms 06 -040 9

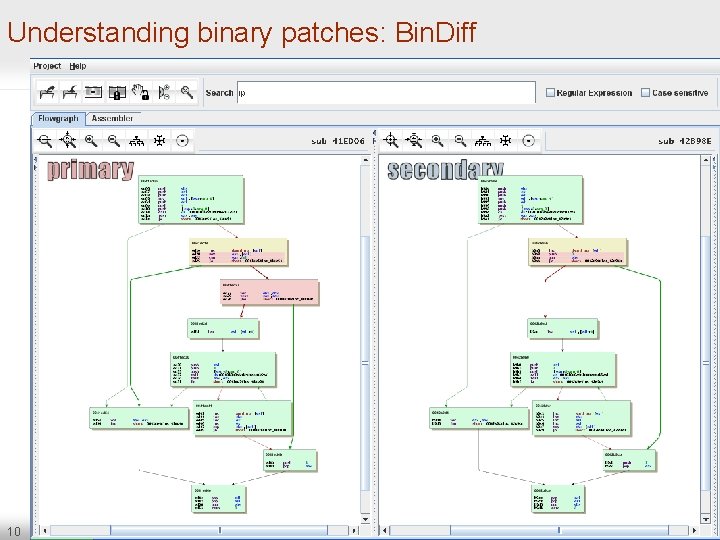
Understanding binary patches: Bin. Diff 10

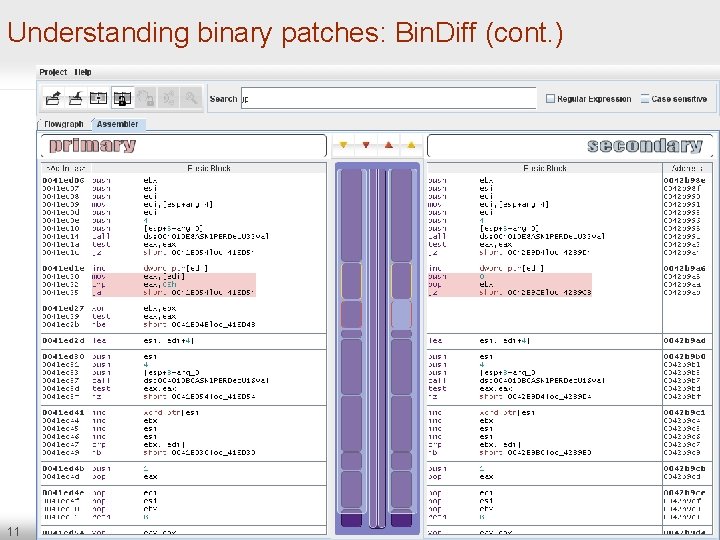
Understanding binary patches: Bin. Diff (cont. ) 11

Metasploit Framework • Framework for vulnerability exploitation and penetration testing • Capabilities – – – – 12 Library of exploit codes Library of payloads (shells, VNC) Victim fingerprinting Opcode database (instruction addresses for various software versions) Exploit encoding (avoiding special character, intrustion and intrusion detection systems) Modular architecture, many add-ons Powerful scriptable command-line interface Convenient GUI and web interfaces

Metasploit Framework (cont. ) • http: //www. metasploit. com/ • Book: Kennedy, O’Gorman, Kearns, Aharoni, Metasplit: The Penetration Tester’s Guide (2011 edition) • Numerous on-line tutorials – Example: https: //www. youtube. com/watch? v=mr. La. Uaowt-w 13

Metasploit Framework: back to MS 06 -040 Demo: https: //www. youtube. com/watch? v=mr. La. Uaowt-w 14

Meanwhile, in theory-land… Fully Homomorphic Encryption 15

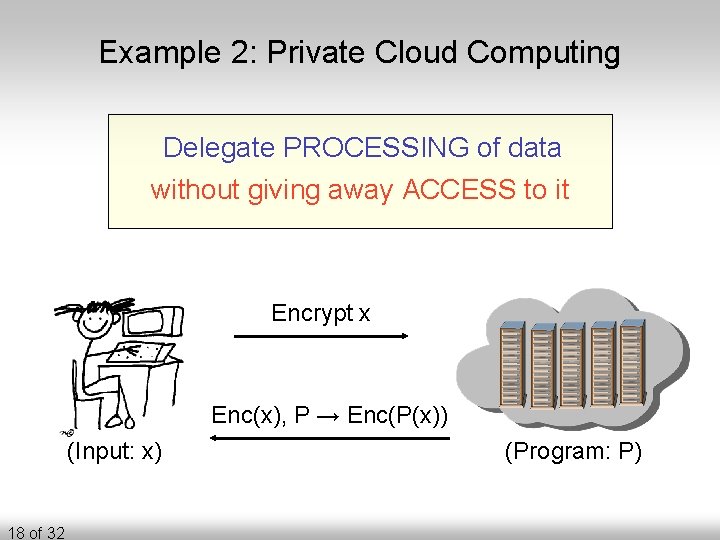
The goal Delegate processing of data without giving away access to it 16 of 32

Example 1: Private Search Delegate PROCESSING of data without giving away ACCESS to it ► You: Encrypt the query, send to Google (Google does not know the key, cannot “see” the query) ► Google: Encrypted query → Encrypted results (You decrypt and recover the search results) 17 of 32

Example 2: Private Cloud Computing Delegate PROCESSING of data without giving away ACCESS to it Encrypt x Enc(x), P → Enc(P(x)) (Input: x) 18 of 32 (Program: P)

Fully Homomorphic Encryption Encrypted x, Program P → Encrypted P(x) Definition: (Key. Gen, Enc, Dec, Eval) (as in regular public/private-key encryption) q Correctness of Eval: For every input x, program P – If c = Enc(PK, x) and c′ = Eval (PK, c, P), then Dec (SK, c′) = P(x). q Compactness: Length of c′ independent of size of P q Security = Semantic Security [GM 82] 19 of 32

Fully Homomorphic Encryption [Rivest-Adleman-Dertouzos’ 78] Enc(x) x Knows nothing of x. Function f Eval: f, Enc(x) Enc(f(x)) homomorphic evaluation 20 of 32

Fully Homomorphic Encryption ► First Defined: “Privacy homomorphism” [RAD’ 78] – their motivation: searching encrypted data 21 of 32

Fully Homomorphic Encryption ► First Defined: “Privacy homomorphism” [RAD’ 78] – their motivation: searching encrypted data ► Limited Variants: – RSA & El Gamal: multiplicatively homomorphic – GM & Paillier: additively homomorphic X c 1 = m 1 e 22 of 32 c 2 = m 2 e c* = c 1 c 2…cn = (m 1 m 2…mn)e mod N cn = mne

Fully Homomorphic Encryption ► First Defined: “Privacy homomorphism” [RAD’ 78] – their motivation: searching encrypted data ► Limited Variants: – RSA & El Gamal: multiplicatively homomorphic – GM & Paillier: additively homomorphic – BGN’ 05 & GHV’ 10: quadratic formulas ► NON-COMPACT homomorphic encryption: 23 of 32 – Based on Yao garbled circuits – SYY’ 99 & MGH’ 08: c* grows exp. with degree/depth – IP’ 07 works for branching programs

Fully Homomorphic Encryption ► First Defined: “Privacy homomorphism” [RAD’ 78] – their motivation: searching encrypted data Big Breakthrough: [Gentry 09] First Construction of Fully Homomorphic Encryption using algebraic number theory & “ideal lattices” ►Full course last semester ►Today: an alternative construction [DGHV’ 10]: – using just integer addition and multiplication – easier to understand, implement and improve 24 of 32

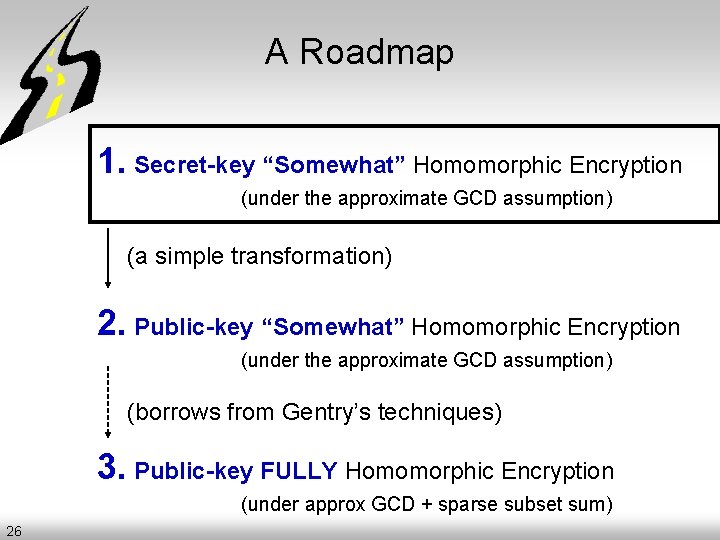
Constructing fully-homomoprhic encryption assuming hardness of approximate GCD 25 of 32

A Roadmap 1. Secret-key “Somewhat” Homomorphic Encryption (under the approximate GCD assumption) (a simple transformation) 2. Public-key “Somewhat” Homomorphic Encryption (under the approximate GCD assumption) (borrows from Gentry’s techniques) 3. Public-key FULLY Homomorphic Encryption (under approx GCD + sparse subset sum) 26

Secret-key Homomorphic Encryption Secret key: a large n 2 -bit odd number p (sec. param = n) To Encrypt a bit b: – pick a random “large” multiple of p, say q·p (q ~ n 5 bits) (r ~ n bits) – pick a random “small” even number 2·r – Ciphertext c = q·p+2·r+b “noise” To Decrypt a ciphertext c: – c (mod p) = 2·r+b – read off the least significant bit 27

Secret-key Homomorphic Encryption How to Add and Multiply Encrypted Bits: – Add/Mult two near-multiples of p gives a near-multiple of p. – c 1 = q 1·p + (2·r 1 + b 1), c 2 = q 2·p + (2·r 2 + b 2) – c 1+c 2 = p·(q 1 + q 2) + 2·(r 1+r 2) + (b 1+b 2) «p LSB = b 1 XOR b 2 – c 1 c 2 = p·(c 2·q 1+c 1·q 2 -q 1·q 2) + 2·(r 1 r 2+r 1 b 2+r 2 b 1) + b 1 b 2 « p LSB = b 1 AND b 2 28

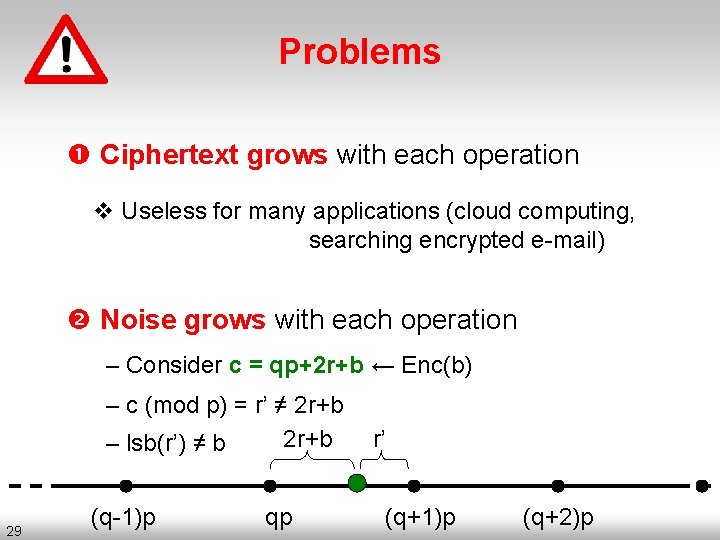
Problems Ciphertext grows with each operation v Useless for many applications (cloud computing, searching encrypted e-mail) Noise grows with each operation – Consider c = qp+2 r+b ← Enc(b) – c (mod p) = r’ ≠ 2 r+b – lsb(r’) ≠ b 29 (q-1)p qp r’ (q+1)p (q+2)p

Problems Ciphertext grows with each operation v Useless for many applications (cloud computing, searching encrypted e-mail) Noise grows with each operation v Can perform “limited” number of hom. operations v What we have: “Somewhat Homomorphic” Encryption 30

Public-key Homomorphic Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) – t+1 encryptions of 0 – Wlog, assume that x 0 is the largest of them To Decrypt a ciphertext c: – c (mod p) = 2·r+b – read off the least significant bit Eval (as before) 31

Public-key Homomorphic Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) To Encrypt a bit b: pick random subset S c= [1…t] + b (mod x 0) To Decrypt a ciphertext c: (mod x 0) a small k) = p[p) = 2·r+b ] + 2[ +b– kx 0 (for – c c(mod p) =] 2·r+b – read= off p[ the least significant ] + 2[ bit ]+b of p) + (“small” even noise) + b Eval (as (mult. before) 32

Public-key Ciphertext Homomorphic Size Reduction Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) To Encrypt a bit b: pick random subset S [1…t] – Resulting ciphertext < x 0 c= + b (mod x 0) – Underlying bit is the same (since x 0 has even noise) –To. Noise Decrypt ciphertext c: by much(*) doesa not increase – c (mod p) = 2·r+b – read off the least significant bit Eval: Reduce mod x 0 after each operation 33 (*) additional tricks for mult

A Roadmap þ Secret-key “Somewhat” Homomorphic Encryption þ Public-key “Somewhat” Homomorphic Encryption 3. Public-key FULLY Homomorphic Encryption 34

How “Somewhat” Homomorphic is this? Can evaluate (multi-variate) polynomials with m terms, and maximum degree d if d << n. or f(x 1, …, xt) = x 1·x 2·xd + … + x 2·x 5·xd-2 m terms Say, noise in Enc(xi) < 2 n Final Noise ~ (2 n)d+…+(2 n)d = m • (2 n)d 35

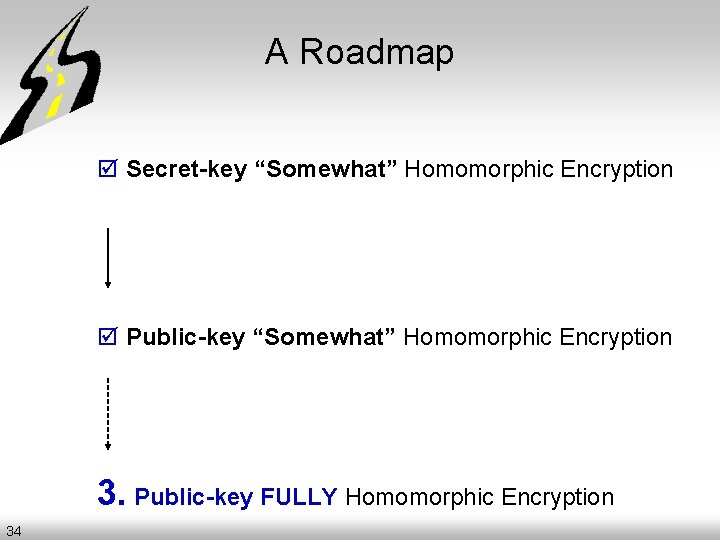
From “Somewhat” to “Fully” Theorem [Gentry’ 09]: Convert “bootstrappable” → FHE = Can eval all fns. Augmented Decryption ckt. “Somewhat” HE “Bootstrappable” NAND Dec 36 c 1 sk Dec c 2 sk

Is our Scheme “Bootstrappable”? What functions can the scheme EVAL? (polynomials of degree < n) (? ) Complexity of the (aug. ) Decryption Circuit (degree ~ n 1. 73 polynomial) Can be made bootstrappable – Similar to Gentry’ 09 Caveat: Assume Hardness of “Sparse Subset Sum” 37

Security (of the “somewhat” homomorphic scheme) 38

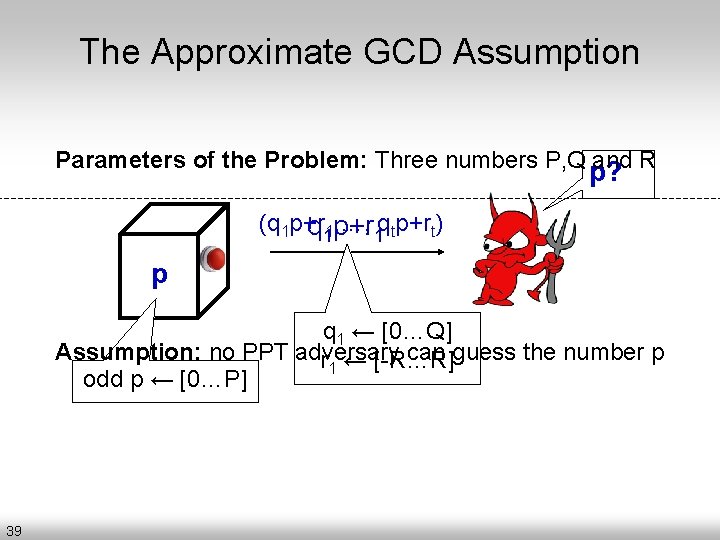
The Approximate GCD Assumption Parameters of the Problem: Three numbers P, Q and R p? (q 1 p+r , …, 1 qtp+rt) q 11 p+r p q 1 ← [0…Q] Assumption: no PPT adversary can guess the number p r 1 ← [-R…R] odd p ← [0…P] 39

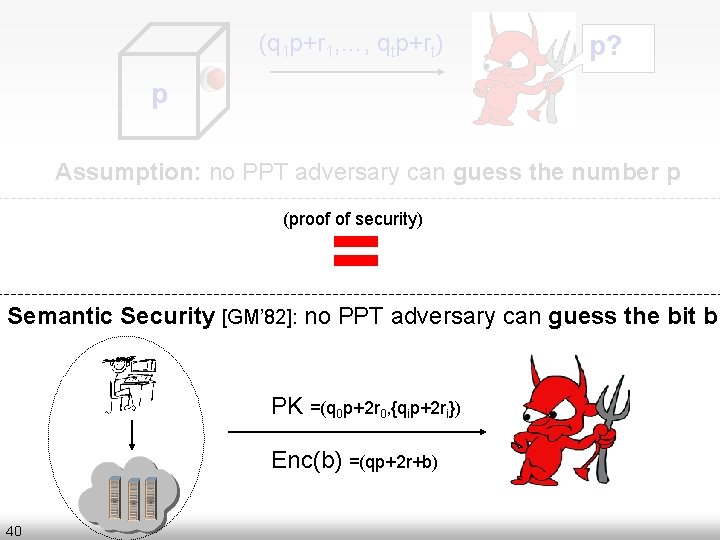
(q 1 p+r 1, …, qtp+rt) p? p Assumption: no PPT adversary can guess the number p = (proof of security) Semantic Security [GM’ 82]: no PPT adversary can guess the bit b PK =(q 0 p+2 r 0, {qip+2 ri}) Enc(b) =(qp+2 r+b) 40

Progress in FHE ►“Galactic” → Efficient [BV 11 a, BV 11 b, BGV 11, GHS 11, LTV 11] – asymptotically: nearly linear-time* algorithms – practically: a few milliseconds for Enc, Dec [LNV 11, GHS 11] ► Strange assumptions → Mild assumptions [BV 11 b, GH 11, BGV 11] – Best Known [BGV 11]: (leveled) FHE from worst-case hardness of n. O(log n)-approx short vectors on lattices 41 *linear-time in the security parameter

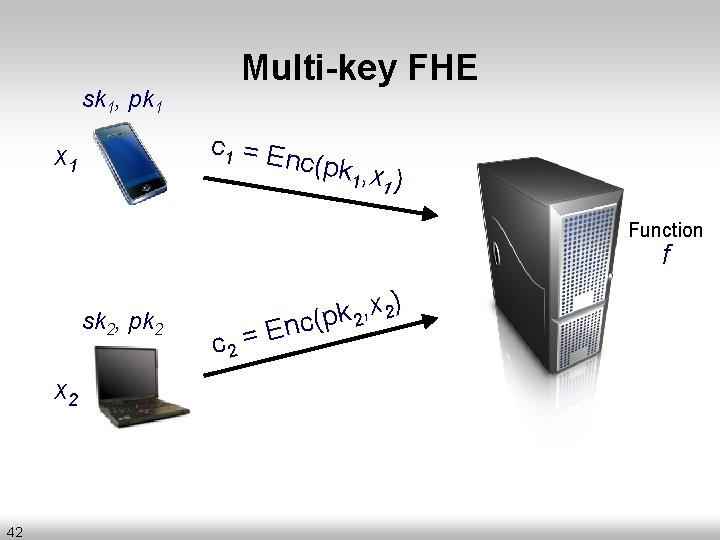
sk 1, pk 1 Multi-key FHE c 1 = En c(pk , x 1 1) x 1 Function f sk 2, pk 2 x 2 42 c 2 = E ) x , 2 k nc(p 2

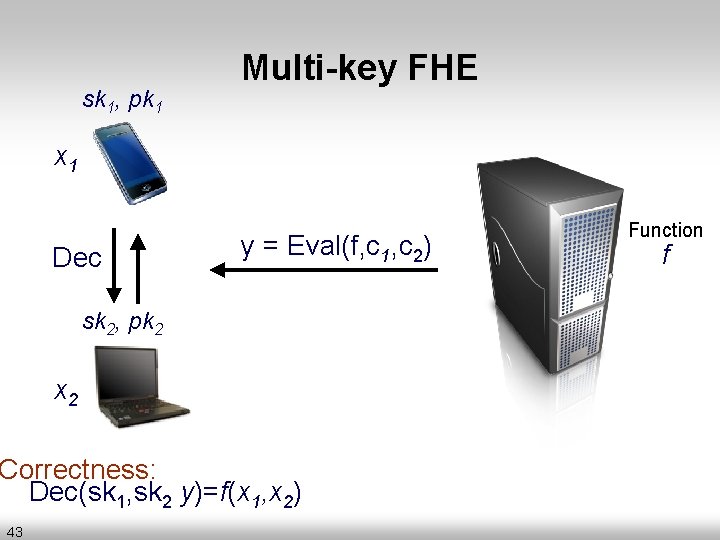
sk 1, pk 1 Multi-key FHE x 1 Dec y = Eval(f, c 1, c 2) sk 2, pk 2 x 2 Correctness: Dec(sk 1, sk 2 y)=f(x 1, x 2) 43 Function f

Fully homomorphic encryption: discussion • Assumptions – Mathematical – Adversarial model • Applicability – Decryption? Keys? • Alternative: multiparty computation – When interaction is free • What about integrity? – Computationally-sound proofs, proof-carrying data 44