Information Retrieval CSE 8337 Spring 2003 Modeling Material

Information Retrieval CSE 8337 Spring 2003 Modeling Material for these slides obtained from: n. Modern Information Retrieval by Ricardo Baeza-Yates and Berthier Ribeiro-Neto http: //www. sims. berkeley. edu/~hearst/irbook/ n. Introduction to Modern Information Retrieval by Gerard Salton and Michael J. Mc. Gill, Mc. Graw-Hill, 1983.

Modeling TOC n n Introduction Classic IR Models n n Set Theoretic Models n n n Boolean Model Vector Model Probabilistic Model Fuzzy Set Model Extended Boolean Model Generalized Vector Model Latent Semantic Indexing Neural Network Model Alternative Probabilistic Models n n Inference Network Belief Network 2

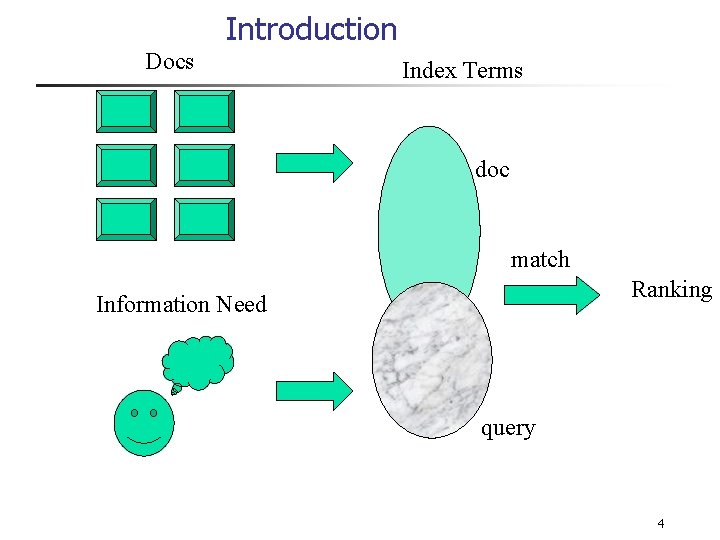
Introduction n n IR systems usually adopt index terms to process queries Index term: n n n Stemming might be used: n n a keyword or group of selected words any word (more general) connect: connecting, connections An inverted file is built for the chosen index terms 3

Introduction Docs Index Terms doc match Ranking Information Need query 4

Introduction n n Matching at index term level is quite imprecise No surprise that users get frequently unsatisfied Since most users have no training in query formation, problem is even worst Frequent dissatisfaction of Web users Issue of deciding relevance is critical for IR systems: ranking 5

Introduction n n A ranking is an ordering of the documents retrieved that (hopefully) reflects the relevance of the documents to the query A ranking is based on fundamental premisses regarding the notion of relevance, such as: n n common sets of index terms sharing of weighted terms likelihood of relevance Each set of premisses leads to a distinct IR model 6

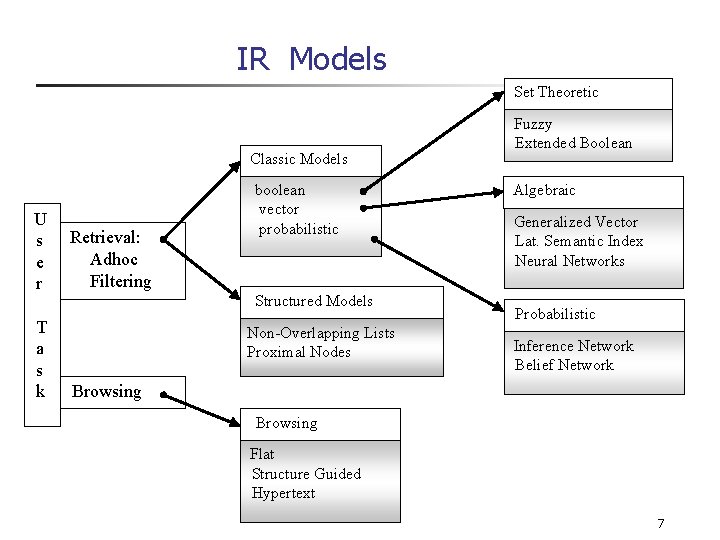
IR Models Set Theoretic Classic Models U s e r T a s k Retrieval: Adhoc Filtering boolean vector probabilistic Structured Models Non-Overlapping Lists Proximal Nodes Fuzzy Extended Boolean Algebraic Generalized Vector Lat. Semantic Index Neural Networks Probabilistic Inference Network Belief Network Browsing Flat Structure Guided Hypertext 7

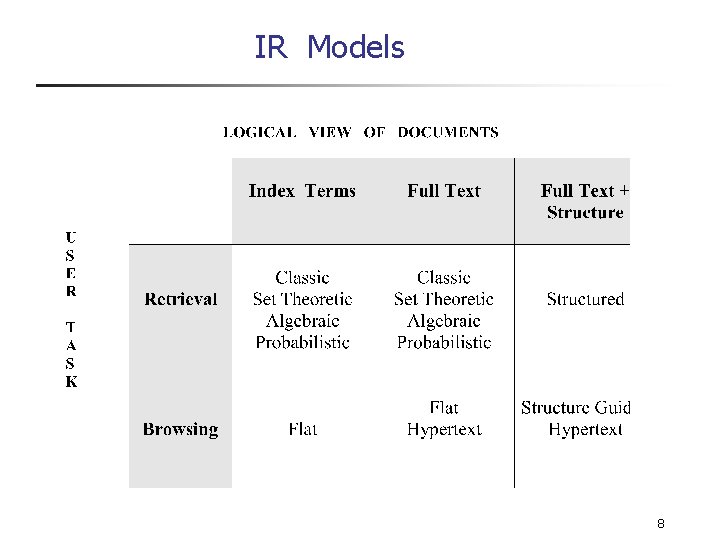
IR Models 8

Classic IR Models - Basic Concepts n n Each document represented by a set of representative keywords or index terms An index term is a document word useful for remembering the document main themes Usually, index terms are nouns because nouns have meaning by themselves However, search engines assume that all words are index terms (full text representation) 9

Classic IR Models - Basic Concepts n n n The importance of the index terms is represented by weights associated to them ki- an index term dj - a document wij - a weight associated with (ki, dj) The weight wij quantifies the importance of the index term for describing the document contents 10

Classic IR Models - Basic Concepts n n t is the total number of index terms K = {k 1, k 2, …, kt} is the set of all index terms n n wij >= 0 is a weight associated with (ki, dj) wij = 0 indicates that term does not belong to doc n n dj= (w 1 j, w 2 j, …, wtj) is a weighted vector associated with the document dj gi(dj) = wij is a function which returns the weight associated with pair (ki, dj) 11

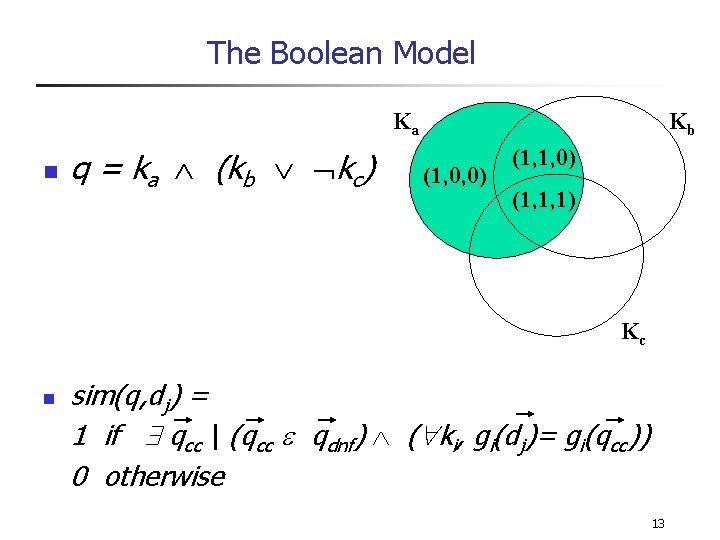
The Boolean Model n n Simple model based on set theory Queries specified as boolean expressions n precise semantics and neat formalism n Terms are either present or absent. Thus, n Consider wij {0, 1} n n n q = ka (kb kc) qdnf = (1, 1, 1) (1, 1, 0) (1, 0, 0) qcc= (1, 1, 0) is a conjunctive component 12

The Boolean Model Ka n q = ka (kb kc) Kb (1, 0, 0) (1, 1, 1) Kc n sim(q, dj) = 1 if qcc | (qcc qdnf) ( ki, gi(dj)= gi(qcc)) 0 otherwise 13

Drawbacks of the Boolean Model n n n Retrieval based on binary decision criteria with no notion of partial matching No ranking of the documents is provided Information need has to be translated into a Boolean expression The Boolean queries formulated by the users are most often too simplistic As a consequence, the Boolean model frequently returns either too few or too many documents in response to a user query 14

The Vector Model n n Use of binary weights is too limiting Non-binary weights provide consideration for partial matches These term weights are used to compute a degree of similarity between a query and each document Ranked set of documents provides for better matching 15

The Vector Model n n n n wij > 0 whenever ki appears in dj wiq >= 0 associated with the pair (ki, q) dj = (w 1 j, w 2 j, . . . , wtj) q = (w 1 q, w 2 q, . . . , wtq) To each term ki is associated a unitary vector i The unitary vectors i and j are assumed to be orthonormal (i. e. , index terms are assumed to occur independently within the documents) The t unitary vectors i form an orthonormal basis for a t-dimensional space where queries and documents are represented as weighted vectors 16

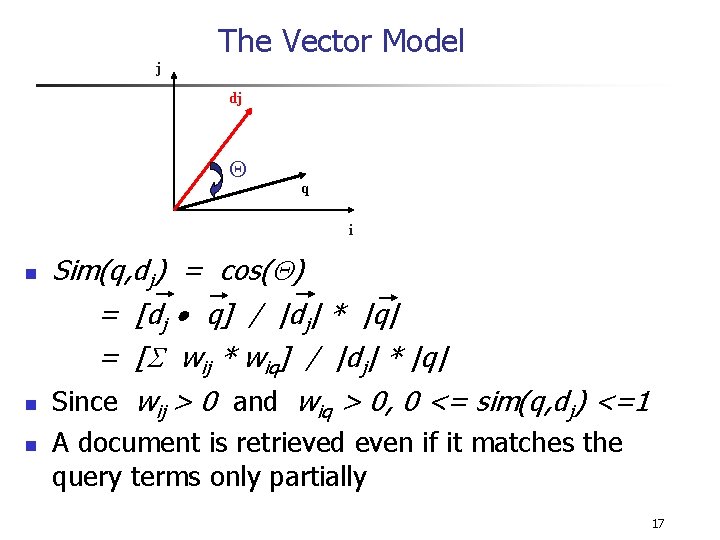
The Vector Model j dj q i n n n Sim(q, dj) = cos( ) = [dj q] / |dj| * |q| = [ wij * wiq] / |dj| * |q| Since wij > 0 and wiq > 0, 0 <= sim(q, dj) <=1 A document is retrieved even if it matches the query terms only partially 17

Weights wij and wiq ? n n One approach is to examine the frequency of the occurence of a word in a document: Absolute frequency: n tf factor, the term frequency within a document n freqi, j - raw frequency of ki within dj n Both high-frequency and low-frequency terms may not actually be significant Relative frequency: tf divided by number of words in document Normalized frequency: fi, j = (freqi, j)/(maxl freql, j) 18

Inverse Document Frequency n n Importance of term may depend more on how it can distinguish between documents. Quantification of inter-documents separation Dissimilarity not similarity idf factor, the inverse document frequency 19

n n n IDF N be the total number of docs in the collection ni be the number of docs which contain ki The idf factor is computed as n n idfi = log (N/ni) the log is used to make the values of tf and idf comparable. It can also be interpreted as the amount of information associated with the term ki. n IDF Ex: n N=1000, n 1=100, n 2=500, n 3=800 n idf 1= 3 - 2 = 1 n idf 2= 3 – 2. 7 = 0. 3 n idf 3 = 3 – 2. 9 = 0. 1 20

The Vector Model n n n The best term-weighting schemes take both into account. wij = fi, j * log(N/ni) This strategy is called a tf-idf weighting scheme 21

The Vector Model n For the query term weights, a suggestion is n n wiq = (0. 5 + [0. 5 * freqi, q / max(freql, q]) * log(N/ni) The vector model with tf-idf weights is a good ranking strategy with general collections The vector model is usually as good as any known ranking alternatives. It is also simple and fast to compute. 22

The Vector Model n Advantages: n n term-weighting improves quality of the answer set partial matching allows retrieval of docs that approximate the query conditions cosine ranking formula sorts documents according to degree of similarity to the query Disadvantages: n Assumes independence of index terms (? ? ); not clear that this is bad though 23

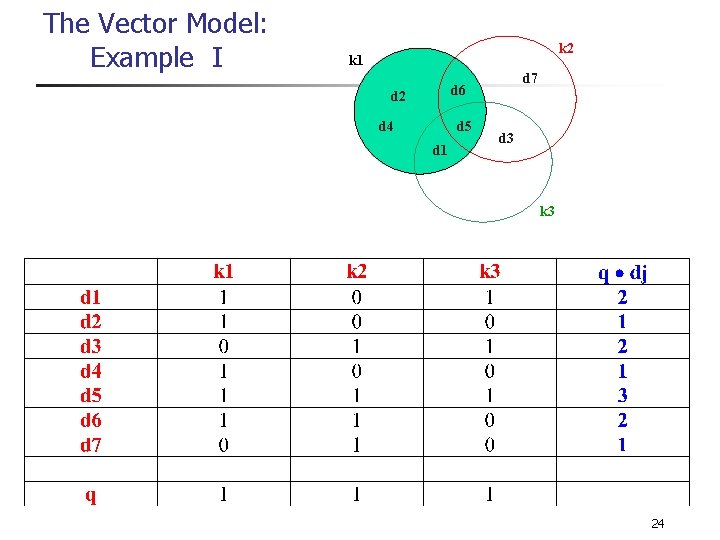
The Vector Model: Example I k 2 k 1 d 7 d 6 d 2 d 4 d 5 d 1 d 3 k 3 24

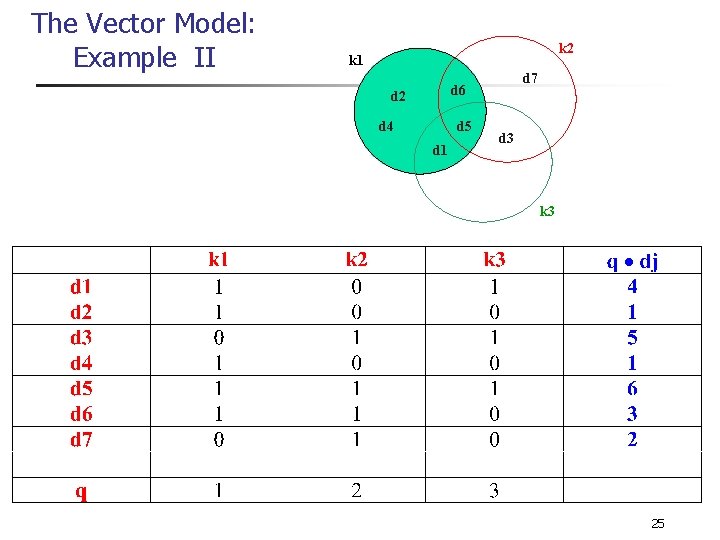
The Vector Model: Example II k 2 k 1 d 7 d 6 d 2 d 4 d 5 d 1 d 3 k 3 25

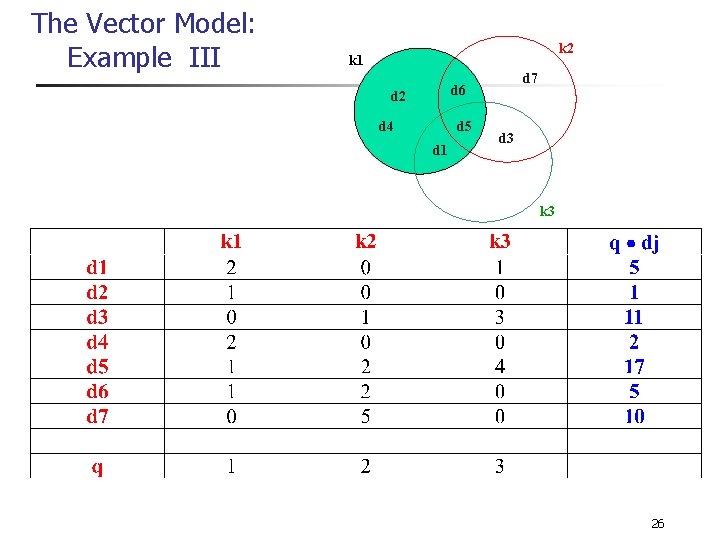
The Vector Model: Example III k 2 k 1 d 7 d 6 d 2 d 4 d 5 d 1 d 3 k 3 26

Probabilistic Model n n n Objective: to capture the IR problem using a probabilistic framework Given a user query, there is an ideal answer set Querying as specification of the properties of this ideal answer set (clustering) But, what are these properties? Guess at the beginning what they could be (i. e. , guess initial description of ideal answer set) Improve by iteration 27

Probabilistic Model n n n An initial set of documents is retrieved somehow User inspects these docs looking for the relevant ones (in truth, only top 10 -20 need to be inspected) IR system uses this information to refine description of ideal answer set By repeting this process, it is expected that the description of the ideal answer set will improve Have always in mind the need to guess at the very beginning the description of the ideal answer set Description of ideal answer set is modeled in probabilistic terms 28

Probabilistic Ranking Principle n n Given a user query q and a document dj, the probabilistic model tries to estimate the probability that the user will find the document dj interesting (i. e. , relevant). Ideal answer set is referred to as R and should maximize the probability of relevance. Documents in the set R are predicted to be relevant. But, n n how to compute probabilities? what is the sample space? 29

The Ranking n Probabilistic ranking computed as: n n sim(q, dj) = P(dj relevant-to q) / P(dj non-relevantto q) This is the odds of the document dj being relevant Taking the odds minimize the probability of an erroneous judgement Definition: n wij {0, 1} P(R | dj) : probability that given doc is relevant n P( R | dj) : probability doc is not relevant n 30

The Ranking n sim(dj, q) = P(R | dj) / P( R | dj) = [P(dj | R) * P(R)] [P(dj | R) * P( R)] ~ P(dj | R) n P(dj | R) : probability of randomly selecting the document dj from the set R of relevant documents 31

The Ranking n sim(dj, q) ~ n ~ P(dj | R) [ P(ki | R)] * [ P( ki | R)] P(ki | R) : probability that the index term ki is present in a document randomly selected from the set R of relevant documents 32

The Ranking n sim(dj, q) ~ log [ P(ki | R)] * [ P( kj | R)] [ P(ki | R)] * [ P( ki | R)] ~ K * [ log P(ki | R) + log P(ki | R) ] P( ki | R) where P( ki | R) = 1 - P(ki | R) 33

The Initial Ranking n n n sim(dj, q) ~ wiq * wij * (log P(ki | R) + log P(ki | R) ) P( ki | R) Probabilities P(ki | R) and P(ki | R) ? Estimates based on assumptions: n P(ki | R) = 0. 5 n P(ki | R) = ni N n Use this initial guess to retrieve an initial ranking n Improve upon this initial ranking 34

Improving the Initial Ranking n Let n n n Reevaluate estimates: n n n V : set of docs initially retrieved Vi : subset of docs retrieved that contain ki P(ki | R) = Vi V P(ki | R) = ni - Vi N-V Repeat recursively 35

Improving the Initial Ranking n To avoid problems with V=1 and Vi=0: n n n P(ki | R) = Vi + 0. 5 V + 1 P(ki | R) = ni - Vi + 0. 5 N-V+1 Also, n n P(ki | R) = Vi + ni/N V + 1 P(ki | R) = ni - Vi + ni/N N-V+1 36

Pluses and Minuses n Advantages: n n Docs ranked in decreasing order of probability of relevance Disadvantages: n n need to guess initial estimates for P(ki | R) method does not take into account tf and idf factors 37

Brief Comparison of Classic Models n n n Boolean model does not provide for partial matches and is considered to be the weakest classic model Salton and Buckley did a series of experiments that indicate that, in general, the vector model outperforms the probabilistic model with general collections This seems also to be the view of the research community 38

Set Theoretic Models n n n The Boolean model imposes a binary criterion for deciding relevance The question of how to extend the Boolean model to accomodate partial matching and a ranking has attracted considerable attention in the past We discuss now two set theoretic models for this: n n Fuzzy Set Model Extended Boolean Model 39

Fuzzy Set Model n This vagueness of document/query matching can be modeled using a fuzzy framework, as follows: n n n with each term is associated a fuzzy set each doc has a degree of membership in this fuzzy set Here, we discuss the model proposed by Ogawa, Morita, and Kobayashi (1991) 40

Fuzzy Set Theory n n A fuzzy subset A of U is characterized by a membership function (A, u) : U [0, 1] which associates with each element u of U a number (u) in the interval [0, 1] Definition n Let A and B be two fuzzy subsets of U. Also, let ¬A be the complement of A. Then, n n n (¬A, u) = 1 - (A, u) (A B, u) = max( (A, u), (B, u)) (A B, u) = min( (A, u), (B, u)) 41

Fuzzy Information Retrieval n n Fuzzy sets are modeled based on a thesaurus This thesaurus is built as follows: n n Let c be a term-term correlation matrix Let ci, l be a normalized correlation factor for (ki, kl): ci, l = ni, l ni + nl - ni, l n n ni: number of docs which contain ki nl: number of docs which contain kl ni, l: number of docs which contain both ki and kl We now have the notion of proximity among index terms. 42

Fuzzy Information Retrieval n The correlation factor ci, l can be used to define fuzzy set membership for a document dj as follows: i, j = 1 - (1 - ci, l) ki d j n n i, j : membership of doc dj in fuzzy subset associated with ki The above expression computes an algebraic sum over all terms in the doc dj 43

Fuzzy Information Retrieval n n A doc dj belongs to the fuzzy set for ki, if its own terms are associated with ki If doc dj contains a term kl which is closely related to ki, we have n n n ci, l ~ 1 i, j ~ 1 index ki is a good fuzzy index for doc 44

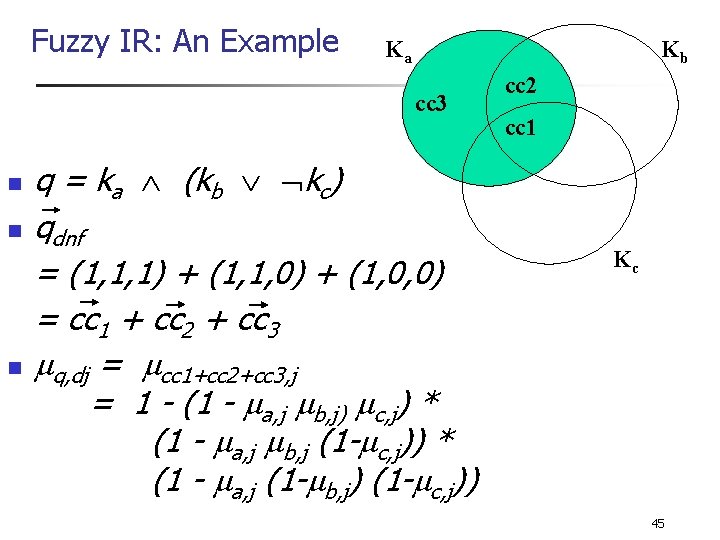
Fuzzy IR: An Example Ka Kb cc 3 n n n q = ka (kb kc) qdnf = (1, 1, 1) + (1, 1, 0) + (1, 0, 0) = cc 1 + cc 2 + cc 3 q, dj = cc 1+cc 2+cc 3, j = 1 - (1 - a, j b, j) c, j) * (1 - a, j b, j (1 - c, j)) * (1 - a, j (1 - b, j) (1 - c, j)) cc 2 cc 1 Kc 45

Fuzzy Information Retrieval n n n Fuzzy IR models have been discussed mainly in the literature associated with fuzzy theory Experiments with standard test collections are not available Difficult to compare at this time 46

Extended Boolean Model n n n Boolean model is simple and elegant. But, no provision for a ranking As with the fuzzy model, a ranking can be obtained by relaxing the condition on set membership Extend the Boolean model with the notions of partial matching and term weighting Combine characteristics of the Vector model with properties of Boolean algebra 47

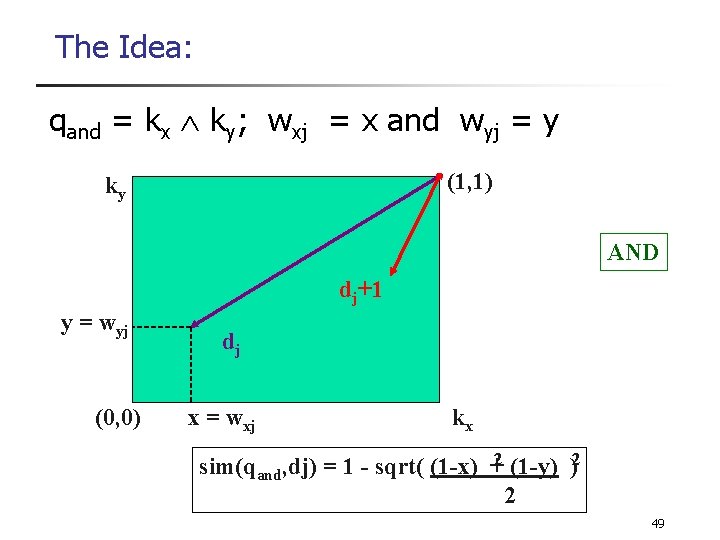
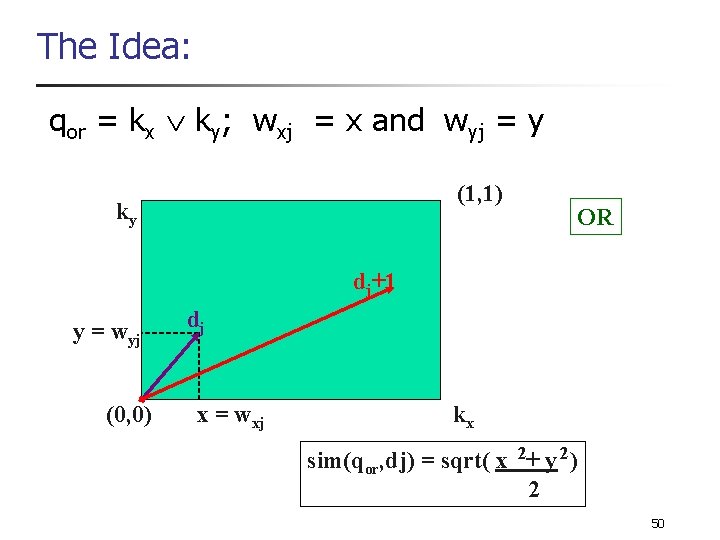
The Idea n n The Extended Boolean Model (introduced by Salton, Fox, and Wu, 1983) is based on a critique of a basic assumption in Boolean algebra Let, n n n q = k x ky wxj = fxj * idfx associated with [kx, dj] max(idfi) Further, wxj = x and wyj = y 48

The Idea: qand = kx ky; wxj = x and wyj = y (1, 1) ky AND dj+1 y = wyj (0, 0) dj x = wxj kx sim(qand, dj) = 1 - sqrt( (1 -x) +2 (1 -y) )2 2 49

The Idea: qor = kx ky; wxj = x and wyj = y (1, 1) ky OR dj+1 y = wyj (0, 0) dj x = wxj kx sim(qor, dj) = sqrt( x 2+ y 2) 2 50

Generalizing the Idea n n We can extend the previous model to consider Euclidean distances in a tdimensional space This can be done using p-norms which extend the notion of distance to include p -distances, where 1 p is a new parameter 51

Generalizing the Idea n A generalized disjunctive query is given by n n qor = k 1 p k 2 p . . . p kt A generalized conjunctive query is given by n n qand = k 1 p k 2 p . . . p kt p p sim(qor, dj) = (x 1 + x 2 +. . . + xm ) m p n p p 1 sim(qand, dj)=1 - ((1 -x 1) + (1 -x 2) +. . . + (1 -xm) ) p m 52

Properties n If p = 1 then (Vector like) n n If p = then (Fuzzy like) n n n sim(qor, dj) = sim(qand, dj) = x 1 +. . . + xm m sim(qor, dj) = max (wxj) sim(qand, dj) = min (wxj) By varying p, we can make the model behave as a vector, as a fuzzy, or as an intermediary model 53

Properties n n This is quite powerful and is a good argument in favor of the extended Boolean model q = (k 1 2 k ) 2 k 3 k 1 and k 2 are to be used as in a vector retrieval while the presence of k 3 is required. n sim(q, dj) = ( (1 - ( (1 -x 1) + (1 -x 2) ) ) + x 3 ) 2 ______ 2 54

Conclusions n n Model is quite powerful Properties are interesting and might be useful Computation is somewhat complex However, distributivity operation does not hold for ranking computation: n n n q 1 = (k 1 k 2) k 3 q 2 = (k 1 k 3) (k 2 k 3) sim(q 1, dj) sim(q 2, dj) 55