INFORMATION NETWORK SECURITY Dr Hassan Shaban RIJNDAEL ALGORITHM

INFORMATION & NETWORK SECURITY Dr. Hassan Shaban

RIJNDAEL ALGORITHM (ADVANCED ENCRYPTION STANDARD) AES • Effective May 26, 2002 the National Institute of Science and Technology (NIST) has selected a block cipher called RIJNDAEL (named after its creators Vincent Rijmen and Joan Daemen) as the symmetric key encryption algorithm to be used to encrypt sensitive information. • AES is an iterated symmetric block cipher, which means that: · AES works by repeating the same defined steps multiple times. · AES is a secret key encryption algorithm. · AES operates on a fixed number of bytes

Block Key size: 128, 192 or 256 bit size: 128, 192, or 256 With Number Key 128 bit: 2128 = 3. 4 x 1038 possible keys of rounds: depends on the key size 10, 12 o 14 scheduling: 44, 52 or 60 sub keys having length = 32 bit Key with variable length (128) • presented with a matrix (array) of bytes with 4 rows

Block size of length 128 bits =16 bytes • presented with a matrix (array) of bytes with 4 rows So bytes 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Will form a matrix: 1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16

AES OPERATION Each round (except the last one) is a uniform and parallel composition of 4 steps • Sub. Bytes (byte-by-byte substitution using an S-box) • Shift. Rows (a permutation, which cyclically shifts the last three rows in the State) • Mix. Columns (substitution that uses Galois Fields, GF(28) arithmetic) • Add. Round key (bit-by-bit XOR with an expanded key)

SUB BYTES TRANSFORMATION During encryption each value of the state is replaced with the corresponding S-BOX value For example HEX 19 would get replaced with HEX D 4

SHIFT ROW Arranges the state in a matrix and then performs a circular shift for each row Each row is then moved over (shifted) 1, 2 or 3 spaces over to the left, depending on the row of the state. First row is never shifted matrix: 1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16 matrix: 1 5 9 13 6 10 14 2 11 15 3 7 16 4 8 12 • During decryption the same process is reversed and all rows are shifted to the right

MIX COLUMN MULTIPLICATION MATRIX GALOIS FIELD MULTIPLICATION The first result byte is calculated by multiplying 4 values of the state column against 4 values of the first row of the matrix. The result of each multiplication is then XORed to produce 1 Byte. Multiplication Matrix 2311 1231 1123 3112 16 byte State b 1 b 5 b 9 b 13 b 2 b 6 b 10 b 14 b 3 b 7 b 11 b 15 b 4 b 8 b 12 b 16 b 1 = (b 1 * 2) XOR (b 2*3) XOR (b 3*1) XOR (b 4*1) b 2 = (b 1 * 1) XOR (b 2*2) XOR (b 3*3) XOR (b 4*1) This procedure is repeated again with the next column of the state b 1 = (b 1 * 2) XOR (b 2*3) XOR (b 3*1) XOR (b 4*1) b 2 = (b 1 * 1) XOR (b 2*2) XOR (b 3*3) XOR (b 4*1) b 3 = (b 1 * 1) XOR (b 2*1) XOR (b 3*2) XOR (b 4*3) b 4 = (b 1 * 3) XOR (b 2*1) XOR (b 3*1) XOR (b 4*2) (b 1= specifies the first byte of the state) The second column will be multiplied against the second row of the matrix in the following manner. b 5 = (b 5 * 2) XOR (b 6*3) XOR (b 7*1) XOR (b 8*1) b 6 = (b 5 * 1) XOR (b 6*2) XOR (b 7*3) XOR (b 8*1) b 7 = (b 5 * 1) XOR (b 6*1) XOR (b 7*2) XOR (b 8*3) b 8 = (b 5 * 3) XOR (b 6*1) XOR (b 7*1) XOR (b 8*2) And so on until all columns of the state are exhausted.

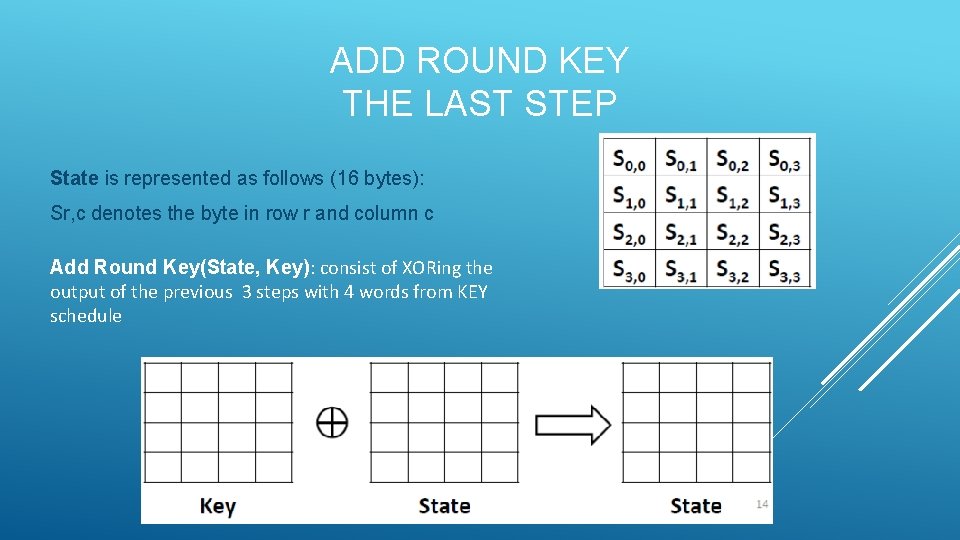
ADD ROUND KEY THE LAST STEP State is represented as follows (16 bytes): Sr, c denotes the byte in row r and column c Add Round Key(State, Key): consist of XORing the output of the previous 3 steps with 4 words from KEY schedule

Problem : Let M be the plain text message M = 0123456789 abcdef 1032547698 badcfe, Where M is in Hexadecimal Format. Let K Be the hexadecimal key K = 133457799 bbcdff 1