Informatik III Christian Schindelhauer Wintersemester 200607 23 Vorlesung

Informatik III Christian Schindelhauer Wintersemester 2006/07 23. Vorlesung 25. 01. 2007 Albert-Ludwigs-Universität Freiburg Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer 1

NP-Vollständigkeit Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØDefinition: – Eine Sprache S ist NP-vollständig, wenn: – S NP – S ist NP-schwierig, d. h. für alle L NP: L ≤m, p S ØLemma: – Sei S eine NP-vollständige Sprache. – Dann ist eine Sprache T ist NP-vollständig, wenn: – T NP – S ≤m, p T Informatik III 22. Vorlesung - 2

NP-Vollständigkeit Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØGegeben ein unbekanntes NP-Problem X, sollte man – nicht nur nach einem Algorithmus mit polynomieller Laufzeit forschen • X P – sondern auch nach einem NP-Vollständigskeitsbeweis ØBeweisideen nicht unbedingt naheliegend … ØBeispiele für NP-Vollständigkeitsbeweise – VERTEX-COVER ist NP-vollständig – (U)HAMPATH ist NP-vollständig – SUBSET-SUM ist NP-vollständig Informatik III 22. Vorlesung - 3

Garey & Johnson Computers and Intractability Informatik III Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer 22. Vorlesung - 4

Wiederholung: 3 -SAT Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØDefinition: – 3 -SAT = { ψ | ψ ist eine erfüllbare Formel in 3 -CNF} – z. B. : Ø 3 -SAT ist NP-vollständig Informatik III 22. Vorlesung - 5

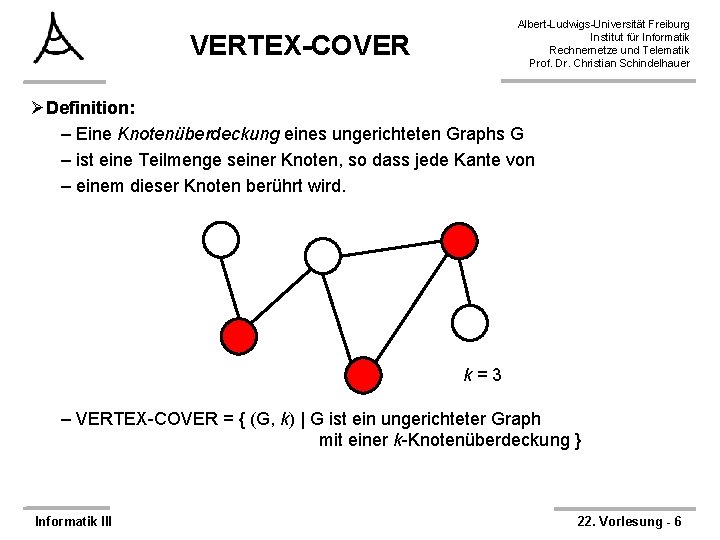
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER ØDefinition: – Eine Knotenüberdeckung eines ungerichteten Graphs G – ist eine Teilmenge seiner Knoten, so dass jede Kante von – einem dieser Knoten berührt wird. k=3 – VERTEX-COVER = { (G, k) | G ist ein ungerichteter Graph mit einer k-Knotenüberdeckung } Informatik III 22. Vorlesung - 6

VERTEX-COVER Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Theorem: – VERTEX-COVER ist NP-vollständig Beweis: – VERTEX-COVER NP: • k-Knotenüberdeckung dient als Zertifikat c § Größe offensichtlich polynomiell in Eingabelänge • Verifizierer A(G=(V, E), k, c) § Prüfe, ob c Kodierung von U V, wobei |U| ≤ k § Für alle Knoten u U markiere alle Kanten {a, b} E mit u {a, b} § Sind alle Kanten markiert, akzeptiere. Sonst verwerfe. • Laufzeit von A polynomiell in der Eingabelänge – z. z. : VERTEX-COVER ist NP-schwierig Informatik III 22. Vorlesung - 7

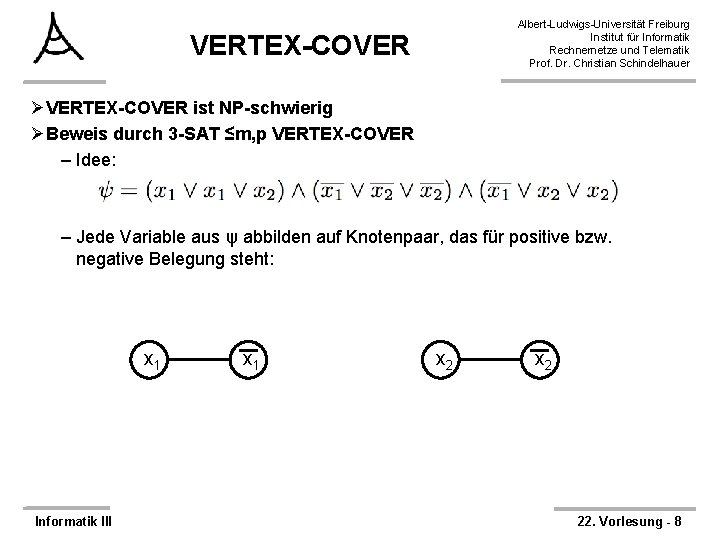
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER ØVERTEX-COVER ist NP-schwierig ØBeweis durch 3 -SAT ≤m, p VERTEX-COVER – Idee: – Jede Variable aus ψ abbilden auf Knotenpaar, das für positive bzw. negative Belegung steht: x 1 Informatik III x 1 x 2 22. Vorlesung - 8

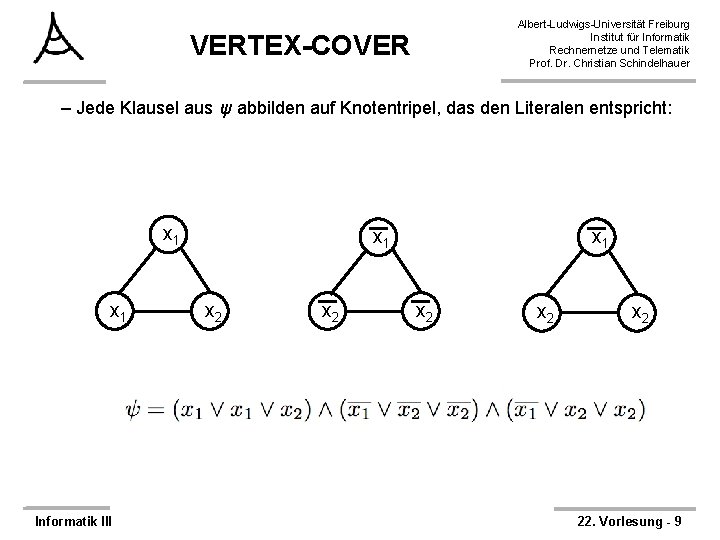
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER – Jede Klausel aus ψ abbilden auf Knotentripel, das den Literalen entspricht: x 1 Informatik III x 1 x 2 x 2 x 2 22. Vorlesung - 9

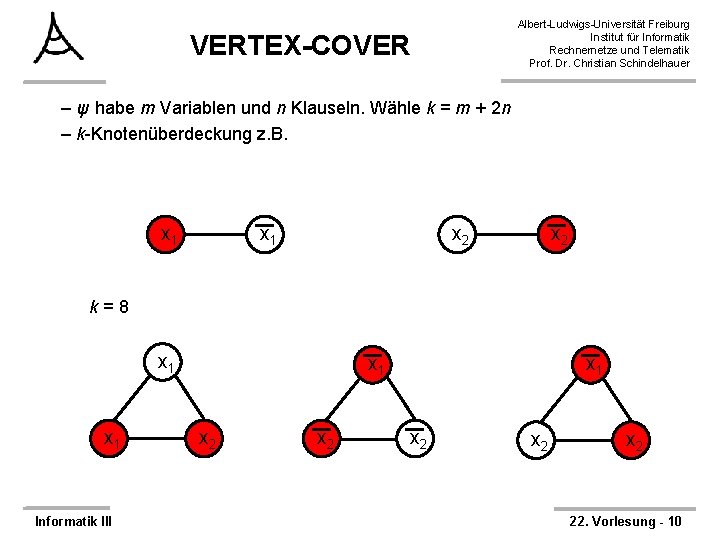
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER – ψ habe m Variablen und n Klauseln. Wähle k = m + 2 n – k-Knotenüberdeckung z. B. x 1 x 2 k=8 x 1 Informatik III x 1 x 2 x 2 x 2 22. Vorlesung - 10

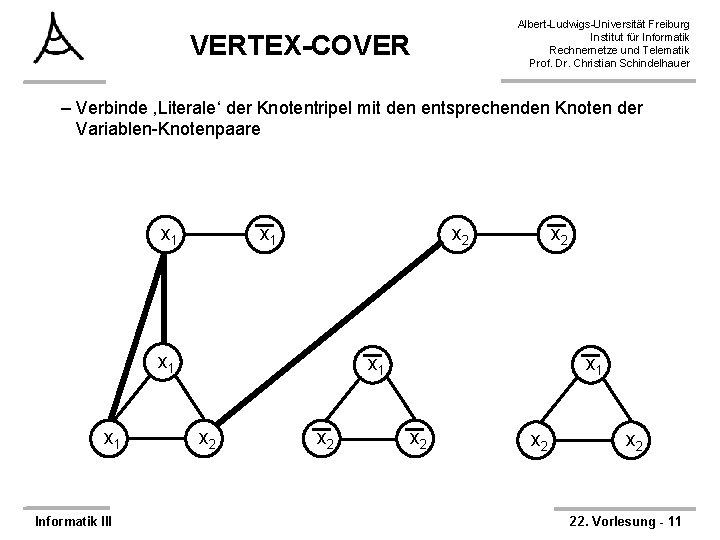
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER – Verbinde ‚Literale‘ der Knotentripel mit den entsprechenden Knoten der Variablen-Knotenpaare x 1 x 2 x 1 Informatik III x 2 x 1 x 2 x 2 22. Vorlesung - 11

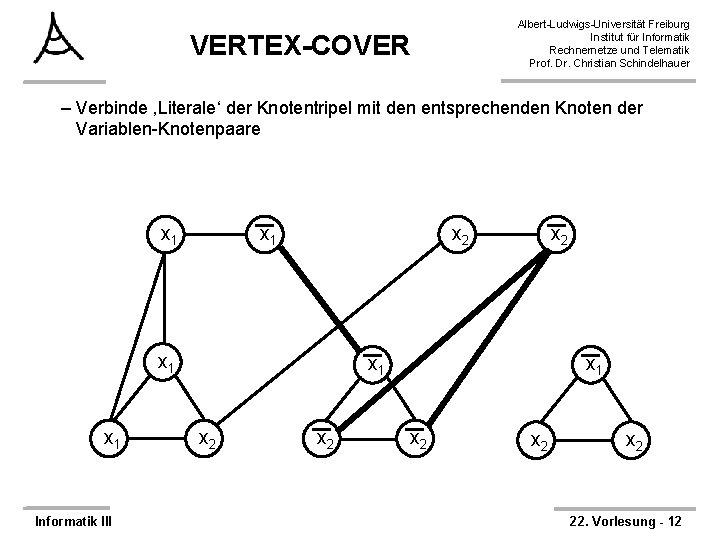
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER – Verbinde ‚Literale‘ der Knotentripel mit den entsprechenden Knoten der Variablen-Knotenpaare x 1 x 2 x 1 Informatik III x 2 x 1 x 2 x 2 22. Vorlesung - 12

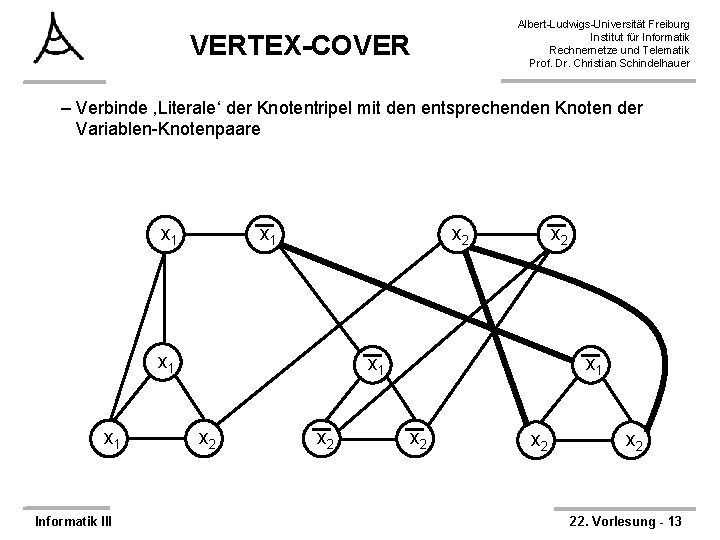
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER – Verbinde ‚Literale‘ der Knotentripel mit den entsprechenden Knoten der Variablen-Knotenpaare x 1 x 2 x 1 Informatik III x 2 x 1 x 2 x 2 22. Vorlesung - 13

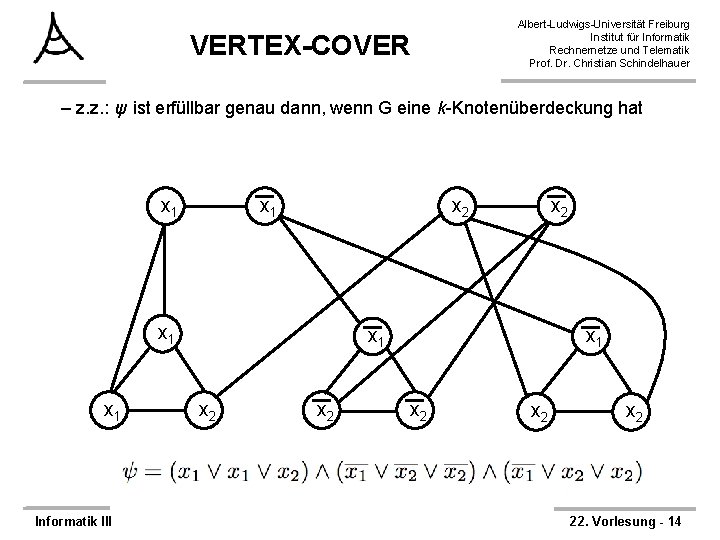
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer VERTEX-COVER – z. z. : ψ ist erfüllbar genau dann, wenn G eine k-Knotenüberdeckung hat x 1 x 2 x 1 Informatik III x 2 x 1 x 2 x 2 22. Vorlesung - 14

VERTEX-COVER Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Øψ ist erfüllbar → G hat eine k-Knotenüberdeckung – Wähle die Knotenüberdeckung wie folgt: – Für jede in der erfüllenden Belegung von ψ mit „wahr“ belegte Variable xi wähle im entsprechenden Knotenpaar in G den Knoten xi; falls xi mit „falsch“ belegt ist den entsprechenden negierten Knoten. – ψ ist erfüllbar → jede Klausel von ψ ist erfüllbar → jede Klausel enthält maximal zwei falsche Literale. Wähle diese Knoten. (Falls weniger als zwei Literale falsch sind, fülle mit beliebigen wahren Literalen auf. ) – Gewählte Knotenüberdeckung hat offensichtlich Größe k Informatik III 22. Vorlesung - 15

VERTEX-COVER Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Gewählte k-Knotenüberdeckung berührt alle Kanten: • Kanten der Knotenpaare, da je einer der beiden gewählt • Kanten der Knotentripel, da je zwei der drei gewählt • Verbindungskanten zu erfüllten Literalen in Variablen-Knotenpaaren abgedeckt • Verbindungskanten zu nicht erfüllten Literalen über Knotentripel abgedeckt Informatik III 22. Vorlesung - 16

VERTEX-COVER Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØG hat eine k-Knotenüberdeckung → ψ ist erfüllbar – In jedem Variablen-Knotenpaar muss genau ein Knoten der Überdeckung angehören. Belege die Variable in ψ dementsprechend. – In jedem Klausel-Knotentripel müssen genau zwei Knoten Teil der Überdeckung sein. Die zu dem dritten Knoten gehörende Verbindungskante muss daher durch einen Variablen-Knoten überdeckt sein → das entsprechende Literal ist wahr → die Klausel ist erfüllt ØTheorem: – VERTEX-COVER ist NP-vollständig Informatik III 22. Vorlesung - 17

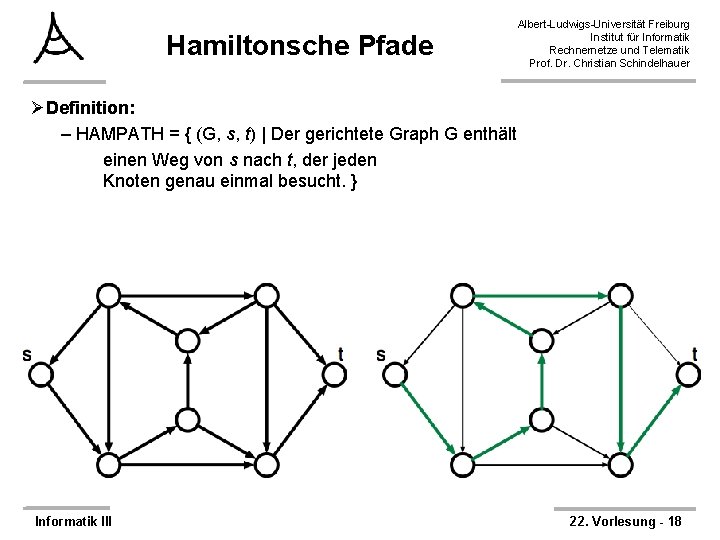
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØDefinition: – HAMPATH = { (G, s, t) | Der gerichtete Graph G enthält einen Weg von s nach t, der jeden Knoten genau einmal besucht. } Informatik III 22. Vorlesung - 18

Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØTheorem: – HAMPATH ist NP-vollständig ØBeweis: – HAMPATH NP: • Hamiltonscher Pfad (s, v 1, v 2, . . . , vn-2, t) dient als Zertifikat c (Größe offensichtlich polynomiell in Eingabelänge) • Verifizierer A(G=(V, E), s, t, c) § Prüfe, ob c Kodierung einer Permutation der Knoten (s, v 1, v 2, . . . , vn-2, t) ist § Für je zwei aufeinander folgende Knoten (x 1, x 2) c, prüfe, ob es eine gerichtete Kante (x 1, x 2) E gibt. Falls nicht, verwerfe. § Akzeptiere. • Laufzeit von A polynomiell in der Eingabelänge – z. z. : HAMPATH ist NP-schwierig Informatik III 22. Vorlesung - 19

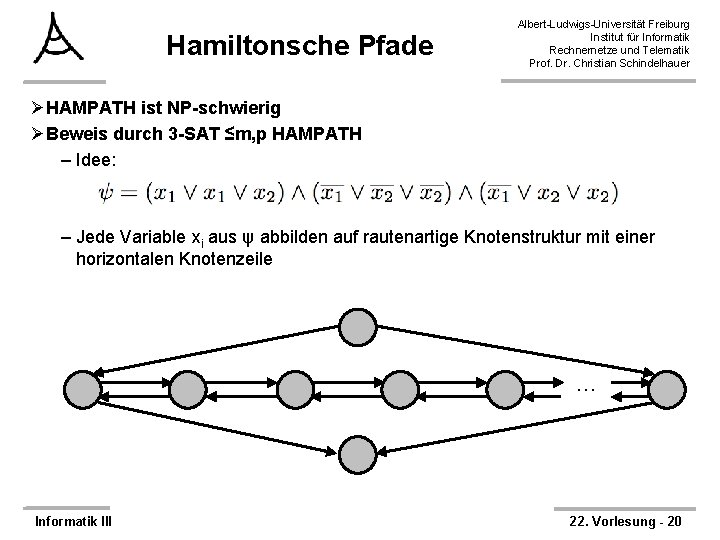
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØHAMPATH ist NP-schwierig ØBeweis durch 3 -SAT ≤m, p HAMPATH – Idee: – Jede Variable xi aus ψ abbilden auf rautenartige Knotenstruktur mit einer horizontalen Knotenzeile … Informatik III 22. Vorlesung - 20

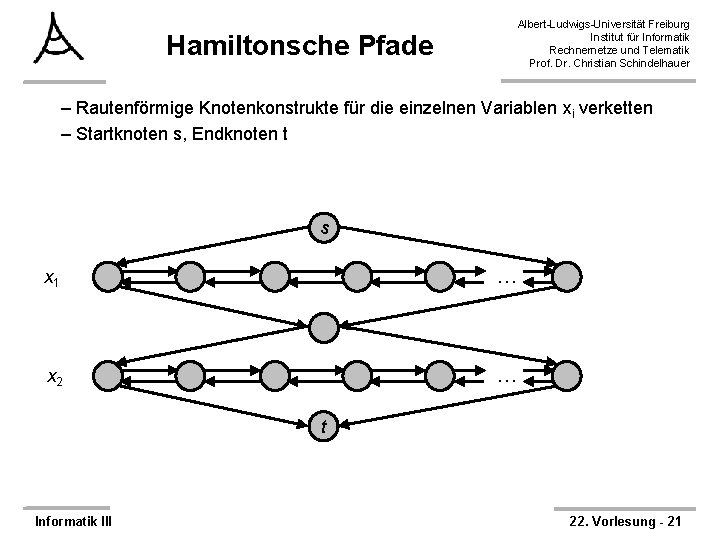
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Rautenförmige Knotenkonstrukte für die einzelnen Variablen xi verketten – Startknoten s, Endknoten t s x 1 … x 2 … t Informatik III 22. Vorlesung - 21

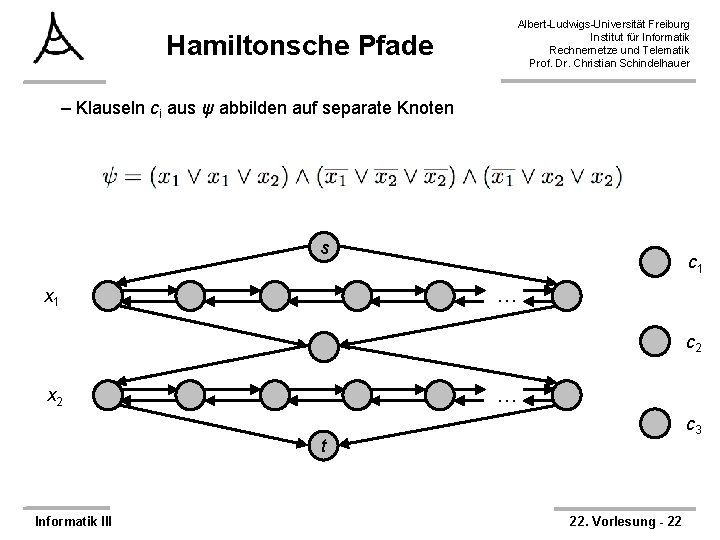
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Klauseln ci aus ψ abbilden auf separate Knoten s c 1 … x 1 c 2 … x 2 c 3 t Informatik III 22. Vorlesung - 22

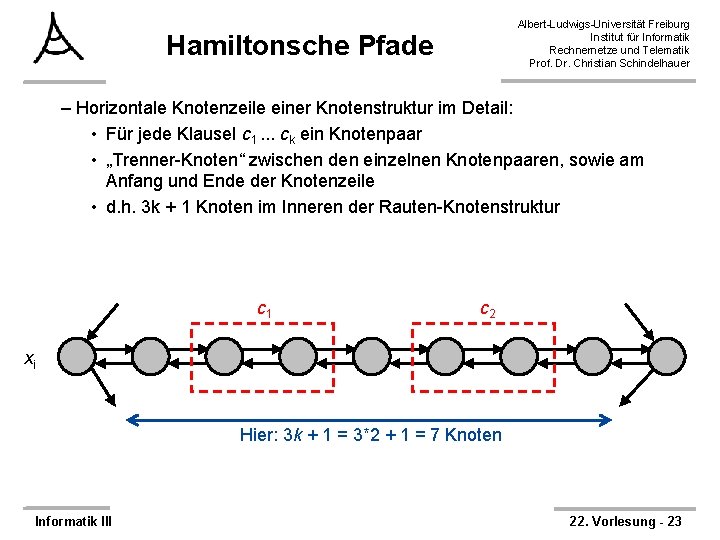
Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Hamiltonsche Pfade – Horizontale Knotenzeile einer Knotenstruktur im Detail: • Für jede Klausel c 1. . . ck ein Knotenpaar • „Trenner-Knoten“ zwischen den einzelnen Knotenpaaren, sowie am Anfang und Ende der Knotenzeile • d. h. 3 k + 1 Knoten im Inneren der Rauten-Knotenstruktur c 1 c 2 xi Hier: 3 k + 1 = 3*2 + 1 = 7 Knoten Informatik III 22. Vorlesung - 23

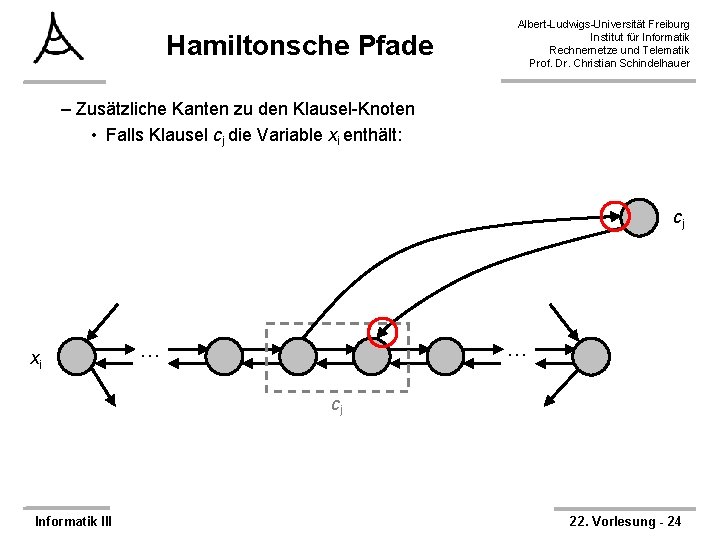
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Zusätzliche Kanten zu den Klausel-Knoten • Falls Klausel cj die Variable xi enthält: cj xi … … cj Informatik III 22. Vorlesung - 24

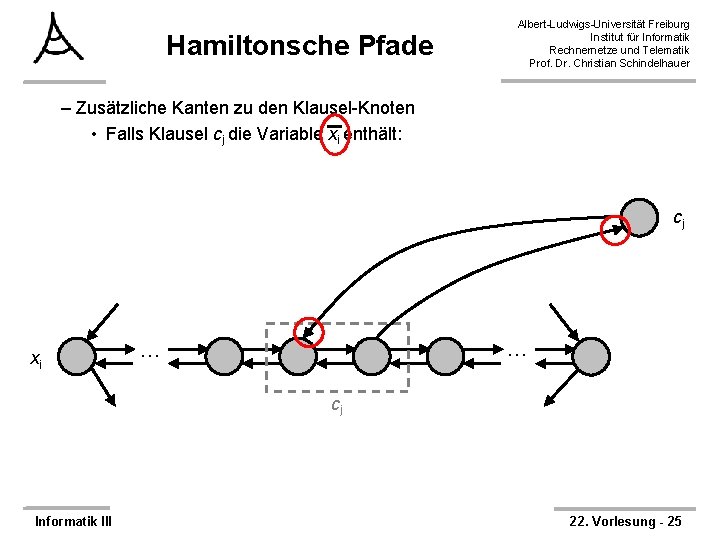
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Zusätzliche Kanten zu den Klausel-Knoten • Falls Klausel cj die Variable xi enthält: cj xi … … cj Informatik III 22. Vorlesung - 25

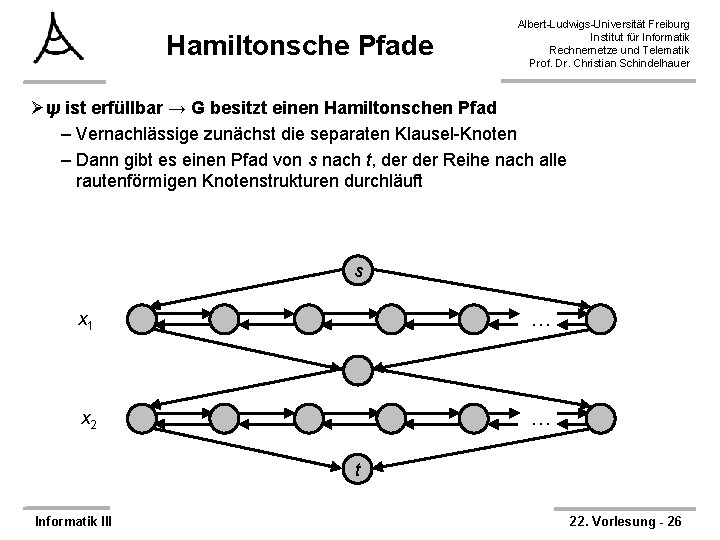
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Øψ ist erfüllbar → G besitzt einen Hamiltonschen Pfad – Vernachlässige zunächst die separaten Klausel-Knoten – Dann gibt es einen Pfad von s nach t, der Reihe nach alle rautenförmigen Knotenstrukturen durchläuft s x 1 … x 2 … t Informatik III 22. Vorlesung - 26

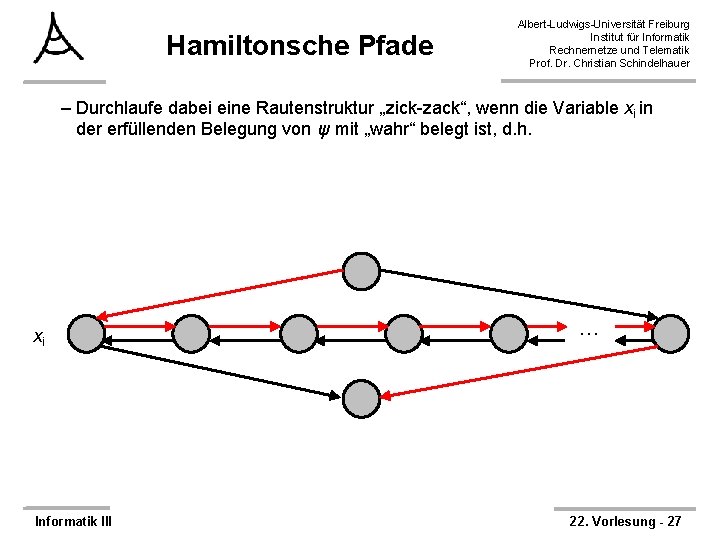
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Durchlaufe dabei eine Rautenstruktur „zick-zack“, wenn die Variable xi in der erfüllenden Belegung von ψ mit „wahr“ belegt ist, d. h. xi Informatik III … 22. Vorlesung - 27

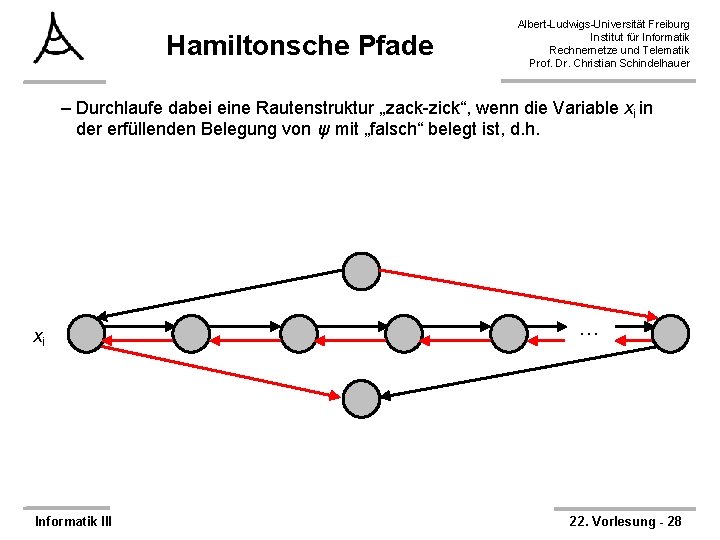
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Durchlaufe dabei eine Rautenstruktur „zack-zick“, wenn die Variable xi in der erfüllenden Belegung von ψ mit „falsch“ belegt ist, d. h. xi Informatik III … 22. Vorlesung - 28

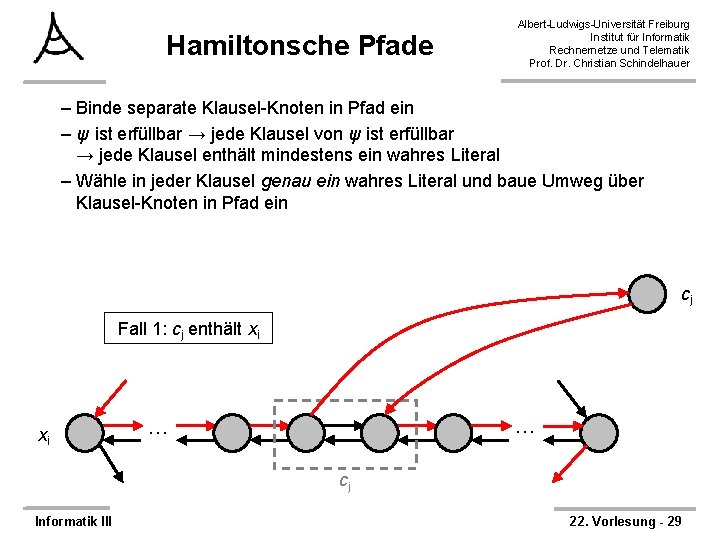
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Binde separate Klausel-Knoten in Pfad ein – ψ ist erfüllbar → jede Klausel von ψ ist erfüllbar → jede Klausel enthält mindestens ein wahres Literal – Wähle in jeder Klausel genau ein wahres Literal und baue Umweg über Klausel-Knoten in Pfad ein cj Fall 1: cj enthält xi xi … … cj Informatik III 22. Vorlesung - 29

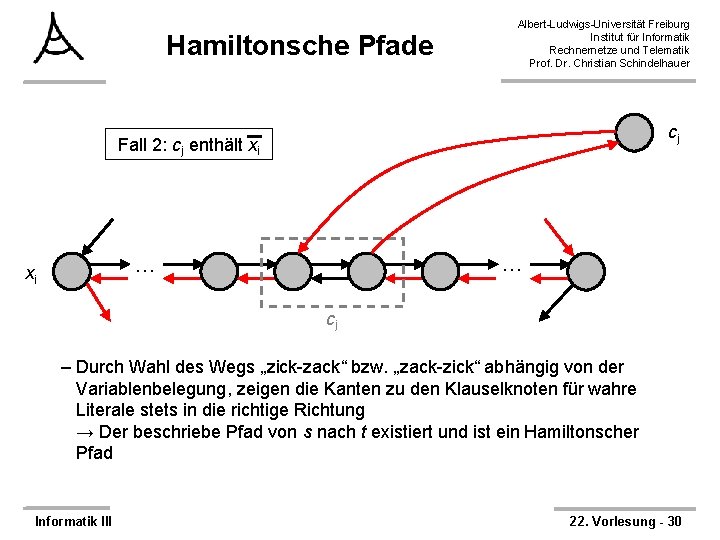
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer cj Fall 2: cj enthält xi … … xi cj – Durch Wahl des Wegs „zick-zack“ bzw. „zack-zick“ abhängig von der Variablenbelegung, zeigen die Kanten zu den Klauselknoten für wahre Literale stets in die richtige Richtung → Der beschriebe Pfad von s nach t existiert und ist ein Hamiltonscher Pfad Informatik III 22. Vorlesung - 30

Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØG besitzt einen Hamiltonschen Pfad → ψ ist erfüllbar – Falls Rautenstrukturen der Reihe nach von oben nach unten durchlaufen werden: • Bestimme Variablenbelegung anhand „zick-zack“ bzw. „zack-zick“ Wegen • Hamiltonscher Pfad besucht alle Knoten, insbesondere auch alle separaten Klauselknoten → nach Konstruktion ist pro Klausel wenigstens ein Literal wahr → jede Klausel ist erfüllbar → ψ ist erfüllbar – Z. z. : Rautenstrukturen werden der Reihe nach von oben nach unten durchlaufen • Umrahmende Kanten der Rautenstrukturen gerichtet → Sprünge nur über Klauselknoten möglich Informatik III 22. Vorlesung - 31

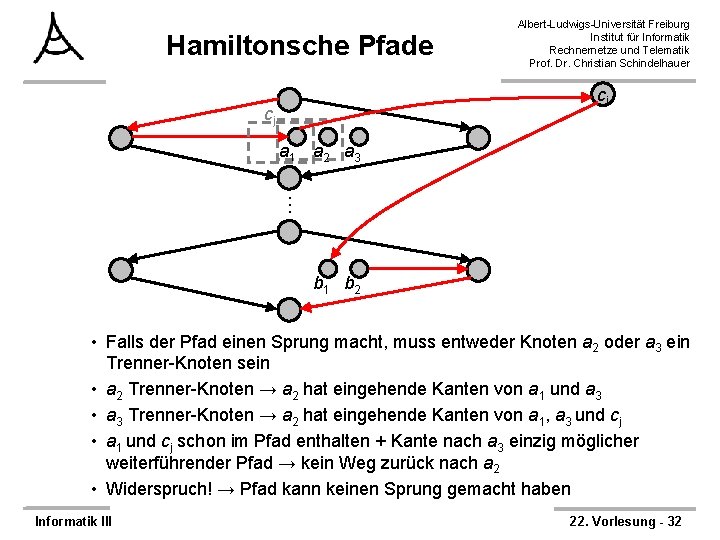
Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer cj cj a 1 a 2 a 3 … b 1 b 2 • Falls der Pfad einen Sprung macht, muss entweder Knoten a 2 oder a 3 ein Trenner-Knoten sein • a 2 Trenner-Knoten → a 2 hat eingehende Kanten von a 1 und a 3 • a 3 Trenner-Knoten → a 2 hat eingehende Kanten von a 1, a 3 und cj • a 1 und cj schon im Pfad enthalten + Kante nach a 3 einzig möglicher weiterführender Pfad → kein Weg zurück nach a 2 • Widerspruch! → Pfad kann keinen Sprung gemacht haben Informatik III 22. Vorlesung - 32

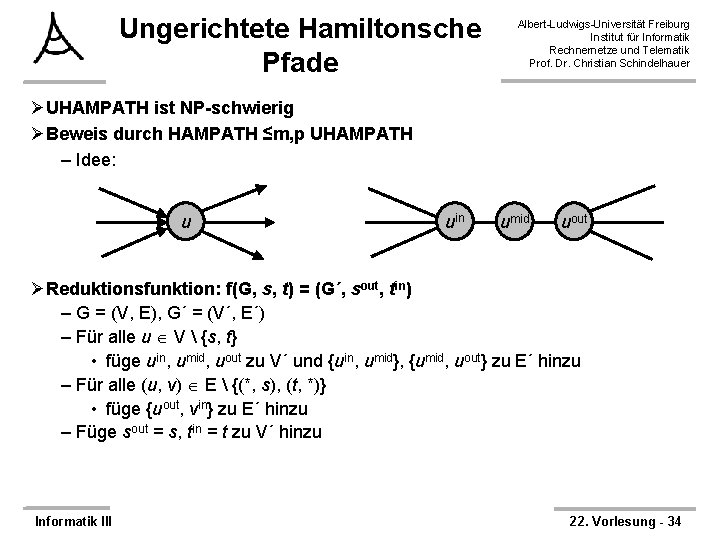
Ungerichtete Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØDefinition: – UHAMPATH = { (G, s, t) | Der ungerichtete Graph G enthält einen Weg von s nach t, der jeden Knoten genau einmal besucht. } ØTheorem: – UHAMPATH ist NP-vollständig ØBeweis: – UHAMPATH NP: Verifizierer analog zu HAMPATH – Z. z. : UHAMPATH ist NP-schwierig Informatik III 22. Vorlesung - 33

Ungerichtete Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØUHAMPATH ist NP-schwierig ØBeweis durch HAMPATH ≤m, p UHAMPATH – Idee: u uin umid uout ØReduktionsfunktion: f(G, s, t) = (G´, sout, tin) – G = (V, E), G´ = (V´, E´) – Für alle u V {s, t} • füge uin, umid, uout zu V´ und {uin, umid}, {umid, uout} zu E´ hinzu – Für alle (u, v) E {(*, s), (t, *)} • füge {uout, vin} zu E´ hinzu – Füge sout = s, tin = t zu V´ hinzu Informatik III 22. Vorlesung - 34

Ungerichtete Hamiltonsche Pfade Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø(G, s, t) HAMPATH → (G´, sout, tin) UHAMPATH – Dem Pfad s, u 1 , u 2, …, uk, t in G entspricht – nach Konstruktion offensichtlich der Pfad – sout, u 1 in, u 1 mid, u 1 out, u 2 in, u 2 mid, u 2 out, …, tin in G´ Ø(G´, sout, tin) UHAMPATH → (G, s, t) HAMPATH – auf sout muss ein uiin folgen – auf alle uiin müssen uimid und uiout folgen – auf alle uiout muss ein ujin folgen (Speziallfall: uiout → tin) – Da es keine Kanten {tin, uiin} E´ gibt, muss der Pfad in tin enden. Weiterhin enthält der Pfad alle Knoten. → Es gibt einen entsprechenden Hamiltonschen Pfad in G Informatik III 22. Vorlesung - 35

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØDefinition SUBSET-SUM: – Gegeben: • Menge von natürlichen Zahlen S = {x 1, . . . , xk} • Ein natürliche Zahl t – Gesucht: • Gibt es eine Teilmenge {y 1, . . . , ym} {x 1, . . . , xk} so dass ØTheorem: – SUBSET-SUM ist NP-vollständig Informatik III 22. Vorlesung - 36

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeweis: – SUBSET-SUM NP: • Teilmenge {y 1, . . . , ym} dient als Zertifikat c (Größe offensichtlich polynomiell in Eingabelänge) • Verifizierer A(S, t, c) § Prüfe, ob c Kodierung einer Teilmenge {y 1, . . . , ym} von S ist § Addiere die Elemente von {y 1, . . . , ym} auf. Falls die Summe t ist, akzeptiere. Andernfalls verwerfe. • Laufzeit von A polynomiell in der Eingabelänge – z. z. : SUBSET-SUM ist NP-schwierig • Beweis durch 3 -SAT ≤m, p SUBSET-SUM Informatik III 22. Vorlesung - 37

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer – Sei ψ eine Boolesche Formel mit Variablen x 1, . . . , xk und Klauseln c 1, . . . , cm. – Konstruiere die Menge S wie folgt: • Für jede Variable xi füge zwei Zahlen yi, zi hinzu • Für jede Klausel cj füge zwei Zahlen gj, hj hinzu • Initialisiere yi, zi mit 10 i+m-1 • Für jedes Literal xi in Klausel cj addiere 10 j-1 zu yi • Für jedes Literal xi in Klausel cj addiere 10 j-1 zu zi • Initialisiere gj, hj mit 10 j-1 – Wähle t als (k+m)-stellige Dezimalzahl, bestehend aus k 1 en gefolgt von m 3 en – Reduktion in polynomieller Zeit durchführbar Informatik III 22. Vorlesung - 38

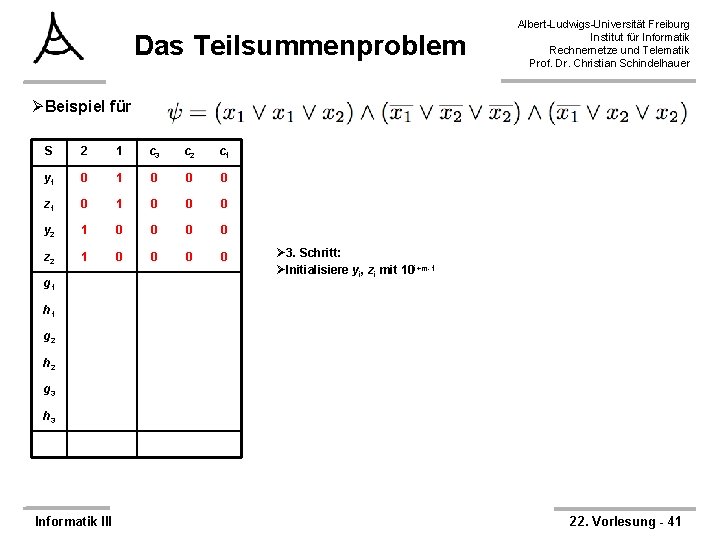
Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 z 1 y 2 z 2 Informatik III Ø 1. Schritt: ØFür jede Variable xi füge zwei Zahlen yi, zi hinzu 22. Vorlesung - 39

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 z 1 y 2 z 2 g 1 Ø 2. Schritt: ØFür jede Klausel cj füge zwei Zahlen gj, hj hinzu h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 40

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 0 z 1 0 0 0 y 2 1 0 0 z 2 1 0 0 g 1 Ø 3. Schritt: ØInitialisiere yi, zi mit 10 i+m-1 h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 41

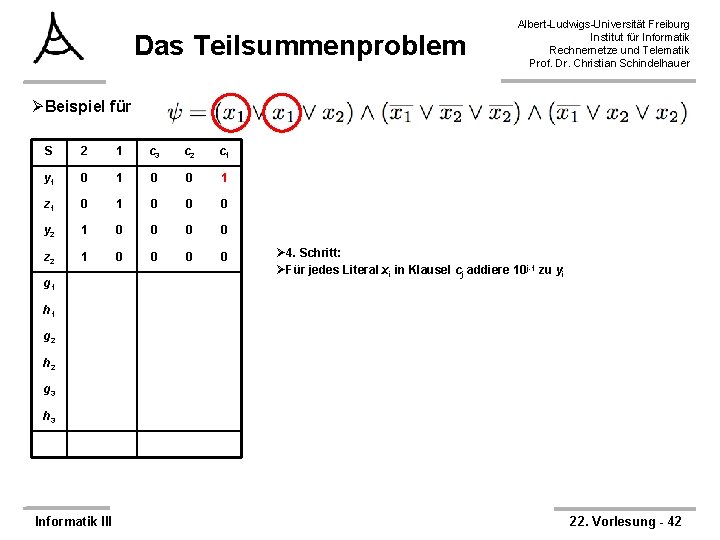
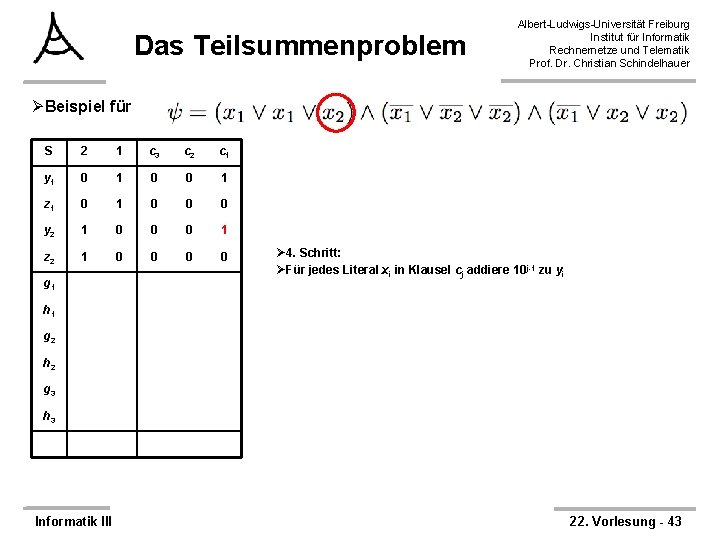
Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 0 0 y 2 1 0 0 z 2 1 0 0 g 1 Ø 4. Schritt: ØFür jedes Literal xi in Klausel cj addiere 10 j-1 zu yi h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 42

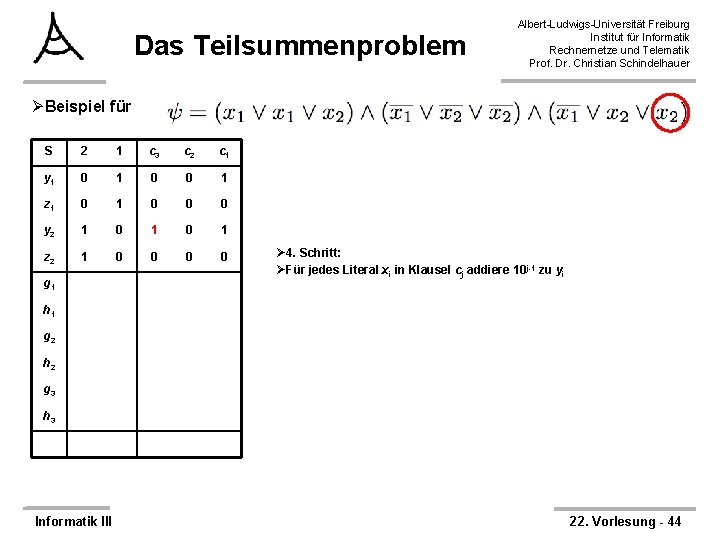
Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 0 0 y 2 1 0 0 0 1 z 2 1 0 0 g 1 Ø 4. Schritt: ØFür jedes Literal xi in Klausel cj addiere 10 j-1 zu yi h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 43

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 0 0 y 2 1 0 1 z 2 1 0 0 g 1 Ø 4. Schritt: ØFür jedes Literal xi in Klausel cj addiere 10 j-1 zu yi h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 44

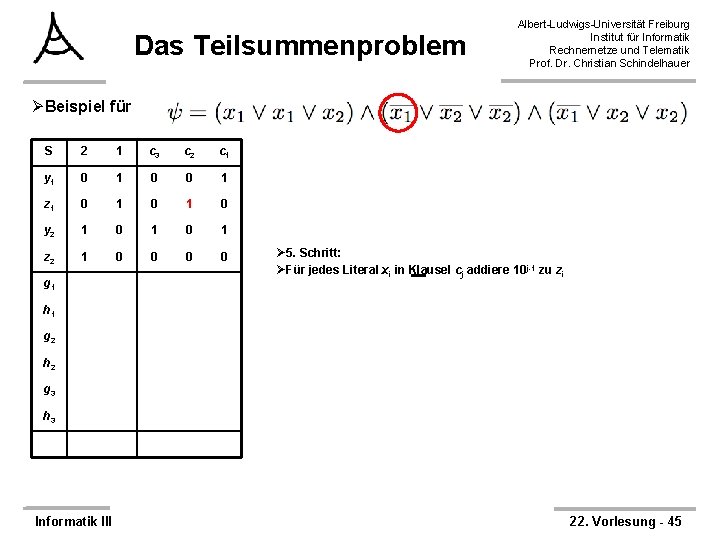
Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 1 0 y 2 1 0 1 z 2 1 0 0 g 1 Ø 5. Schritt: ØFür jedes Literal xi in Klausel cj addiere 10 j-1 zu zi h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 45

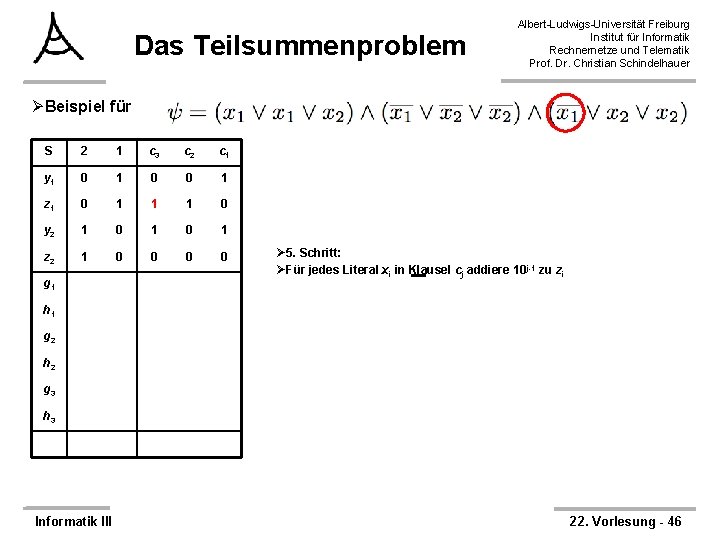
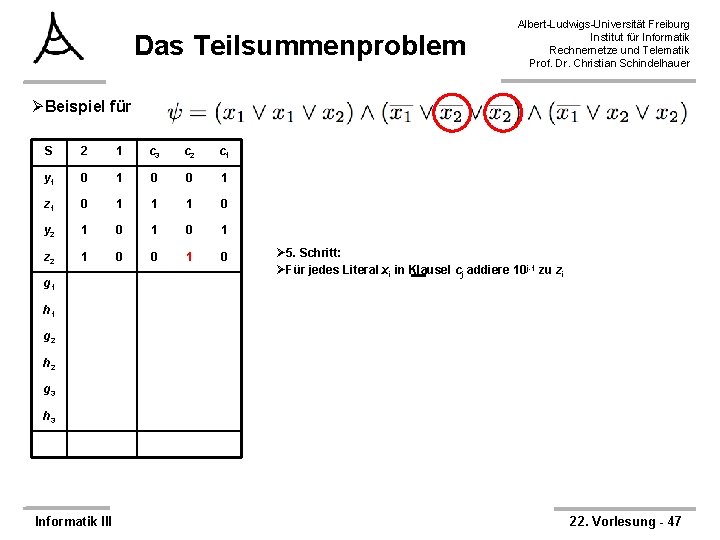
Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 1 1 1 0 y 2 1 0 1 z 2 1 0 0 g 1 Ø 5. Schritt: ØFür jedes Literal xi in Klausel cj addiere 10 j-1 zu zi h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 46

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 1 1 1 0 y 2 1 0 1 z 2 1 0 0 1 0 g 1 Ø 5. Schritt: ØFür jedes Literal xi in Klausel cj addiere 10 j-1 zu zi h 1 g 2 h 2 g 3 h 3 Informatik III 22. Vorlesung - 47

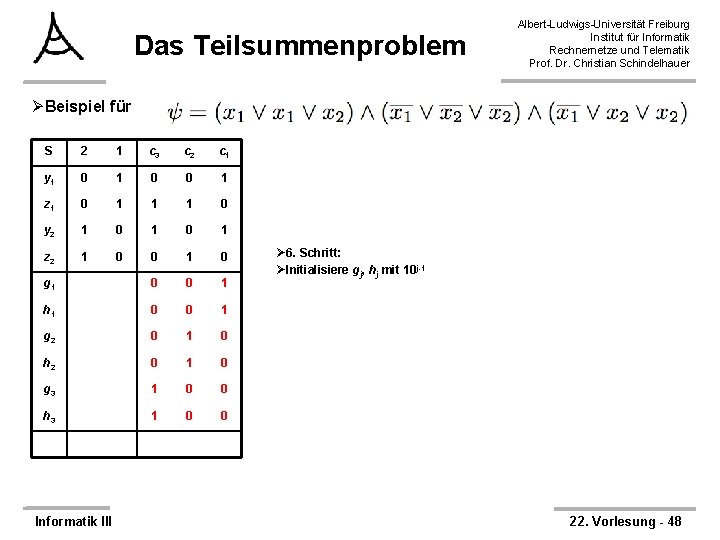
Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 1 1 1 0 y 2 1 0 1 z 2 1 0 0 1 0 g 1 0 0 1 h 1 0 0 1 g 2 0 1 0 h 2 0 1 0 g 3 1 0 0 h 3 1 0 0 Informatik III Ø 6. Schritt: ØInitialisiere gj, hj mit 10 j-1 22. Vorlesung - 48

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 1 1 1 0 y 2 1 0 1 z 2 1 0 0 1 0 g 1 0 0 1 h 1 0 0 1 g 2 0 1 0 h 2 0 1 0 g 3 1 0 0 h 3 1 0 0 3 3 3 t 1 Informatik III 1 Ø 7. Schritt: ØWähle t als (k+m)-stellige Dezimalzahl, bestehend aus k 1 en gefolgt von m 3 en 22. Vorlesung - 49

Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Das Teilsummenproblem Øψ 3 -SAT → (S, t) SUBSET-SUM – Falls xi wahr in erfüllender Belegung, füge yi zur Teilsumme hinzu, andernfalls zi – Die linken k Stellen von t sind 1 en – ψ erfüllbar → jede Klausel erfüllbar → in der Summe wenigstens eine 1 pro Klausel-Spalte → fülle Teilsumme mit gi, hi auf, so dass jede Klausel-Spalte in der Summe 3 hat – Damit (S, t) SUBSET-SUM S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 1 1 1 0 y 2 1 0 1 z 2 1 0 0 1 0 g 1 0 0 1 h 1 0 0 1 g 2 0 1 0 h 2 0 1 0 g 3 1 0 0 h 3 1 0 0 3 3 3 t Informatik III 1 1 22. Vorlesung - 50

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel für S 2 1 c 3 c 2 c 1 y 1 0 0 1 z 1 0 1 1 1 0 y 2 1 0 1 z 2 1 0 0 1 0 Øψ ist erfüllbar (x 1 = falsch, x 2 = wahr) g 1 0 0 1 Øes gibt eine Teilmenge {z 1, y 2, g 1, h 1, g 2, h 2, g 3} von S, deren Summe t ist h 1 0 0 1 g 2 0 1 0 h 2 0 1 0 g 3 1 0 0 h 3 1 0 0 3 3 3 t 1 Informatik III 1 22. Vorlesung - 51

Das Teilsummenproblem Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø(S, t) SUBSET-SUM → ψ 3 -SAT – Beobachtungen: • alle Ziffern der Zahlen aus S sind entweder 0 oder 1 • in jeder Klausel-Spalte können nach Konstruktion niemals mehr als fünf 1 en stehen → es kann keinen Übertrag geben • Damit die linken k Stellen von t 1 en sind, muss in der Teilsumme für jedes i entweder yi oder zi enthalten sein – Falls die Teilsumme yi enthält, setze xi = „wahr“, • andernfalls (zi in Teilsumme) setze xi = „falsch“ – Teilsumme hat eine 3 in allen Klausel-Spalten – Potentielle Summanden gi, hi können max. 2 beitragen → yi, zi in Teilsumme haben min. eine 1 pro Klausel-Spalte → jede Klausel erfüllbar → ψ erfüllbar Informatik III 22. Vorlesung - 52

Ende der 23. Vorlesung Albert-Ludwigs-Universität Freiburg Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Wintersemester 2006/07 23. Vorlesung 25. 01. 2007 53