Informatik III Arne Vater Wintersemester 200607 28 Vorlesung

Informatik III Arne Vater Wintersemester 2006/07 28. Vorlesung 09. 02. 2007 Albert-Ludwigs-Universität Freiburg Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer 1

Die Chomsky. Klassifizierung Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØChomsky-Hierachien – 3: Reguläre Grammatiken – 2: Kontextfreie Grammatiken – 1: Wachsende kontextsensitive Grammatiken – 0: Allgemeine Grammatiken ØAlternative Beschreibung – Reguläre Sprachen und endliche Automaten – Kontextfreie Sprachen und Kellerautomaten – Wachsende kontextsensitive Sprachen und linearer Platz – Chomsky-0 -Sprachen und Rekursiv aufzählbare Sprachen Informatik III 28. Vorlesung - 2

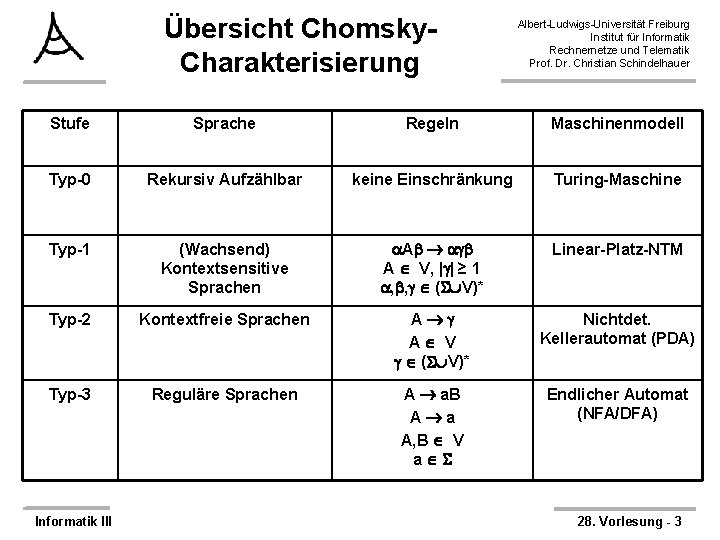
Übersicht Chomsky. Charakterisierung Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Stufe Sprache Regeln Maschinenmodell Typ-0 Rekursiv Aufzählbar keine Einschränkung Turing-Maschine Typ-1 (Wachsend) Kontextsensitive Sprachen A V, | | ≥ 1 , , ( V)* Linear-Platz-NTM Typ-2 Kontextfreie Sprachen A A V ( V)* Nichtdet. Kellerautomat (PDA) Typ-3 Reguläre Sprachen A a. B A a A, B V a Endlicher Automat (NFA/DFA) Informatik III 28. Vorlesung - 3

Chomsky-3: Reguläre Sprachen und endliche Automaten Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Definition – Eine (rechts)-reguläre Grammatik ist ein Vierer-Tupel G = (V, , R, S), wobei • V ist die endliche Menge der Variablen (Nichtterminale) • ist die endliche Menge der Terminale (Terminalsymbole) • R ist eine endliche Menge an Ersetzungsregeln (Regeln/Produktionen) § Jede Regel bildet eine Variable auf ein Terminal * A a, mit A V und a § oder auf ein Wort aus einem Terminal und einer Variable ab * A a. B mit A, B V und a • S V ist die Startvariable § oder die Startvariable wird auf das leere Wort abgebildet * S Ø Beispiel – ({S, T}, {0, 1}, {S 0 S, S 0, S 1 T, T 1 S, , T 0 T}, S} Ø Theorem – Die Menge der regulären Sprachen werden durch die rechts-regulären Grammatiken beschrieben Informatik III 28. Vorlesung - 4

Chomsky-3: Reguläre Sprachen und endliche Automaten Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØTheorem – Die Menge der regulären Sprachen werden durch die rechts-regulären Grammatiken beschrieben. ØBeweis: Rückrichtung – Rechts-reguläre Grammatiken können durch nicht-deterministische endliche Automaten beschrieben werden • Zustandsmenge: Q = V {Qakz} • Startzustand: S • Akzeptierende Zustandsmenge: {Qakz} • Bei Regel A a. B wird B zur Menge von (A, a) hinzugefügt, so dass § B (A, a) (A a. B) R • Bei Regel A a wird Qakz zur Menge von (A, a) hinzugefügt, so dass § Qakz (A, a) (A a) R • Bei Regel S wird Qakz zur Menge von (S, ) hinzugefügt, so dass § Qakz (S, ) (S ) R Informatik III 28. Vorlesung - 5

Chomsky-3: Reguläre Sprachen und endliche Automaten Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØTheorem – Die Menge der regulären Sprachen werden durch die rechts-regulären Grammatiken beschrieben. ØBeweis: Hinrichtung – Deterministische endliche Automaten können durch rechts-reguläre Grammatiken beschrieben werden • Variablen: V = Q • Startsymbol ist der Startzustand • Terminale sind das Alphabet der Sprache • Falls (A, a) = B füge Regel A a. B hinzu § (A, a) = B (A a. B) R • Falls (A, a) = B und B ist akzeptierender Zustand füge Regel A a hinzu § (A, a) = B und B ist akzeptierend (A a) R Informatik III 28. Vorlesung - 6

Beispiel Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Bei Regel A a. B wird B zur Menge von (A, a) hinzugefügt, so dass – B (A, a) (A a. B) R Ø Bei Regel A a wird Qakz zur Menge von (A, a) hinzugefügt, so dass – Qakz (A, a) (A a) R Ø Bei Regel S wird Qakz zur Menge von (S, ) hinzugefügt, so dass – Qakz (S, ) (S ) R Ø ({S, T}, {0, 1}, {S 0 S, S 0, S 1 T, T 1 S, , T 0 T}, S} Ø Falls (A, a) = B füge Regel A a. B hinzu – (A, a) = B (A a. B) R Ø Falls (A, a) = B und B ist akzeptierender Zustand füge Regel A a hinzu – (A, a) = B und B ist akzeptierend (A a) R Informatik III 28. Vorlesung - 7

Chomsky-2: Kontextfreie Sprachen und PDA Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Definition – Eine kontextfreie Grammatik ist ein Vierer-Tupel G = (V, , R, S), wobei • V ist die endliche Menge der Variablen (Nichtterminale) • ist die endliche Menge der Terminale (Terminalsymbole) § V und sind disjunkte Mengen • R ist eine endliche Menge an Ersetzungsregeln (Regeln/Produktionen) § Jede Regel besteht aus einer Variable und einer Zeichenkette aus Variablen und Terminalen, * A w, mit A V, w (V )* • S V ist die Startvariable Ø Ableitung – Falls die Regel A w in R ist, dann ist u. Av uwv, d. h. • u. Av kann zu uwv in einem Schritt abgeleitet werden – Wir sagen das u zu v abgeleitet werden kann oder u * v, wenn es ein k ≥ 0 gibt mit § u u 1 u 2 . . . uk v Ø Sprache der Grammatik G – L(G) = { w * | S * v} Ø Die kontextfreien Sprachen werden durch kontextfreie Grammatiken erzeugt. Informatik III 28. Vorlesung - 8

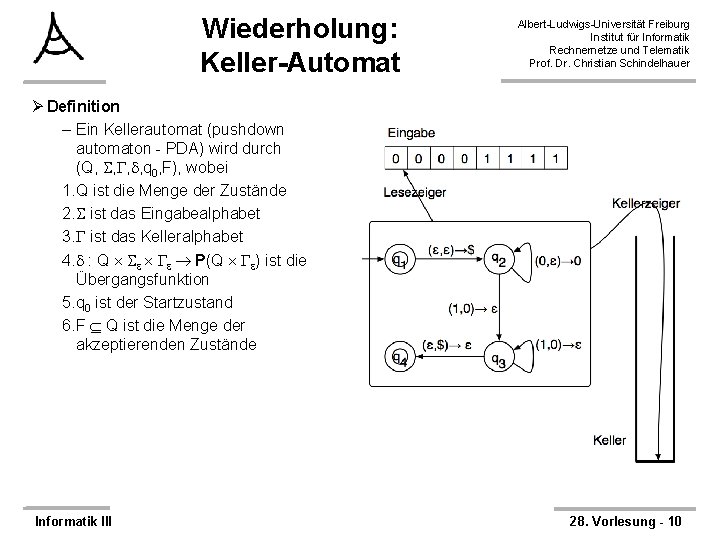
Wiederholung: Keller-Automat Ø Definition – Ein Kellerautomat (pushdown automaton - PDA) wird durch (Q, , , , q 0, F) beschrieben, wobei 1. Q ist die Menge der Zustände 2. ist das Eingabealphabet 3. ist das Kelleralphabet 4. : Q P(Q ) ist die Übergangsfunktion 5. q 0 ist der Startzustand 6. F Q ist die Menge der akzeptierenden Zustände Informatik III Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Ein PDA akzeptiert w, – wenn es w = w 1 w 2. . . wm mit wi gibt – und q = r 0 r 1. . . rm mit si Q gibt – und s 0, s 1, . . . , sm * gibt, so dass Ø r 0 = q 0 und s 0 = Startzustand mit leeren Keller Ø Für i = 0, . . . , m-1 gilt: (ri+1, b) (ri, wi+1, a), wobei si = at und si+1 = bt für passende a, b , t * • rm F 28. Vorlesung - 9

Wiederholung: Keller-Automat Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Definition – Ein Kellerautomat (pushdown automaton - PDA) wird durch (Q, , , , q 0, F), wobei 1. Q ist die Menge der Zustände 2. ist das Eingabealphabet 3. ist das Kelleralphabet 4. : Q P(Q ) ist die Übergangsfunktion 5. q 0 ist der Startzustand 6. F Q ist die Menge der akzeptierenden Zustände Informatik III 28. Vorlesung - 10

Keller-Automaten beschreiben genau die kontextfreien Sprachen Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØTheorem – Eine Sprache ist genau dann kontextfrei, wenn ein Kellerautomat sie erkennt ØBeweisideen – Hinrichtung • durch Bau eines Kellerautomaten der die Regeln im Keller rät • und dann beim Einlesen der Eingabe verifiziert – Rückrichtung • durch spezielle Variablen A[pq] die Zustände bei gleicher Höhe des Kellers beschreiben • Dadurch ergeben sich die Ableitungen § relativ aufwändige Konstruktion Informatik III 28. Vorlesung - 11

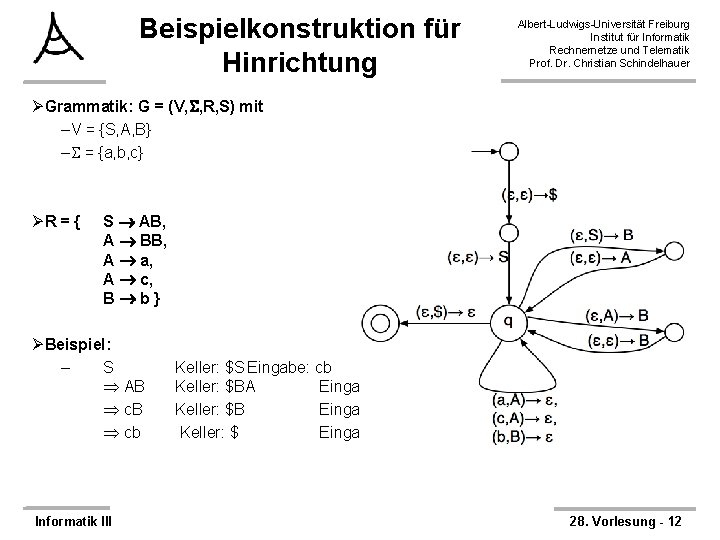
Beispielkonstruktion für Hinrichtung Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØGrammatik: G = (V, , R, S) mit –V = {S, A, B} – = {a, b, c} ØR = { S AB, A BB, A a, A c, B b } ØBeispiel: – S AB cb Informatik III Keller: $S Eingabe: cb Keller: $BA Eingabe: cb Keller: $B Eingabe: b Keller: $ Eingabe: - 28. Vorlesung - 12

Chomsky-1: (Wachsend) Kontextsensitive Sprachen und NSPACE(n) Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Definition (Wachsend) Kontextsensitive Grammatik – Eine wachsend kontext-sensitive Grammatik ist ein Vierer-Tupel G = (V, , R, S), mit • Variablen V (Nichtterminale) • Terminalen und • einer Regelmenge R § Jede Regel besteht aus einer Variable und einem Kontext , , wobei die Variable auf ein Wort mindestens der Länge 1 abgebildet wird: § A mit A V, | | ≥ 1, , , ( V)* § oder S • S V ist die Startvariable – Die kontextsensitive Grammatiken produzieren die kontextsensitiven Sprachen CSL Ø Theorem – CSL = NSPACE(n) Informatik III 28. Vorlesung - 13

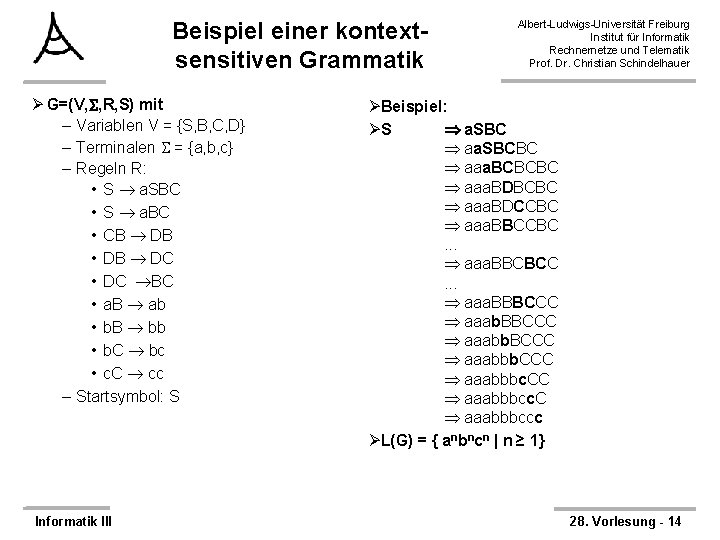
Beispiel einer kontextsensitiven Grammatik Ø G=(V, , R, S) mit – Variablen V = {S, B, C, D} – Terminalen = {a, b, c} – Regeln R: • S a. SBC • S a. BC • CB DB • DB DC • DC BC • a. B ab • b. B bb • b. C bc • c. C cc – Startsymbol: S Informatik III Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØBeispiel: ØS a. SBC aa. SBCBC aaa. BCBCBC aaa. BDCCBC aaa. BBCCBC. . . aaa. BBCBCC. . . aaa. BBBCCC aaabb. BCCC aaabbbc. CC aaabbbccc ØL(G) = { anbncn | n ≥ 1} 28. Vorlesung - 14

Chomsky-1: (Wachsend) Kontextsensitive Sprachen und NSPACE(n) Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØTheorem – CSL = NSPACE(n) ØBeweisidee – CSL NSPACE(n) • NTM M rät die Ableitungen bis die Eingabewortläge erreicht wird • M akzeptiert, falls die Eingabe abgeleitet worden ist • Problem: nichthaltende wiederholende Berechnungspfade • Lösung: § M führt einen Zähler, der mit jeder geratenen Produktion um eins erhöht wird. § Überschreitet der Zähler 2 c n, für geeignete Konstante c, dann verwirft M • Diese Lösung funktioniert, da höchstens 2 cn mögliche Zwischenschritte in der minimalen Ableitung einer kontextsensitiven Sprache vorkommen Informatik III 28. Vorlesung - 15

Chomsky-1: (Wachsend) Kontextsensitive Sprachen und NSPACE(n) Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Theorem – CSL = NSPACE(n) Ø Beweisidee – CSL NSPACE(n) • Betrachte 1 -Band-NTM mit linearem Platz, die genau auf der Eingabe rechnet und keine weiteren Symbole des Bandes bearbeitet • Die Berechnung der 1 -Band-NTM wird rückwärts dargestellt • Für jedes Eingabesymbol a wird durch eine Variable A und ein Terminal a dargestellt • Am Anfang wird eine akzeptierende Konfiguration erzeugt durch entsprechende Regeln: Von Startsymbol S “Qakz _ _ _. . _ “ • Für jeden Übergang (q, a) (q’, r, b) der NTM führe zwei Variablen § X[(q, a) (q’, r, b)] und Y[(q, a) (q’, r, b)] ein • Nun werden für (q, a) (q’, r, b) die folgenden Produktionen eingfügt § B Q’ X[(q, a) (q’, r, b)]Q’ § X[(q, a) (q’, r, b)]Q’ X[(q, a) (q’, r, b)] Y[(q, a) (q’, r, b)] § X[(q, a) (q’, r, b)] Y[(q, a) (q’, r, b)] Q Y[(q, a) (q’, r, b)] § Q Y[(q, a) (q’, r, b)] QA • Übergänge (q, a) (q’, l, b) werden analog bearbeitet • Damit wird die Berechnung rückwärts dargestellt • Am Ende werden die Terminale A a eingesetzt: Die “Rückwärtsrechnung hält” Informatik III 28. Vorlesung - 16

Chomsky-0: Allgemeine Grammatiken und Rekursiv Aufzählbar Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØDefinition Allgemeine (Chomsky-0) Grammatik – Eine allgemeine (Chomsky-0) Grammatik ist ein Vierer-Tupel G = (V, , R, S), mit • Variablen V (Nichtterminale) • Terminalen und • einer Regelmenge R § Jede Regel besteht aus einem Wort ( V)* auf der linken Seite und einem Wort ( V)* auf der rechten § Jede Regel mit , ( V)* ist erlaubt • S V ist die Startvariable ØTheorem – Die allgemeinen Grammatiken beschreiben genau die Menge der rekursiv aufzählbaren Sprachen Informatik III 28. Vorlesung - 17

Chomsky-0: Allgemeine Grammatiken und Rekursiv Aufzählbar Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer ØTheorem – Die allgemeinen Grammatiken beschreiben genau die Menge der rekursiv aufzählbaren Sprachen ØBeweisidee – Hinrichtung: • NTM rät eine Ableitung und versucht dadurch aus dem Startsymbol das Eingabe-Wort abzuleiten • Falls keine Ableitung möglich, hält die NTM nie – Rückrichtung • Berechnung einer NTM wird umgekehrt • Ausgehend von der (eindeutigen) Endkonfiguration mit leerem Band (als Startsymbol) wird jeder Konfigurationsübergang durch lokale kontextsensitive Ableitungsregeln beschrieben § wie bei der Konstruktion für kontextsensitive Sprachen • Blank-Symbole am rechten Speicherrand können durch verkürzende kontextsensitive Regeln erzeugt und wieder freigegeben werden Informatik III 28. Vorlesung - 18

Zusammenfassung der Vorlesung Albert-Ludwigs-Universität Freiburg Institut für Informatik Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Ø Formale Sprachen Ø Komplexitätstheorie – Chomsky-0 = Rekursiv Aufzählbar – DTM, NTM – Chomsky-1 = Kontextsensitiv = NSpace(n) • Bänder, Konfigurationen – Chomsky-2 = Kontextfrei = PDA – TIME(T(n)), NTIME(T(n)) • Pumping-Lemma – P, NP – Chomsky-3 = Regulär = NFA = DFA = • Abbildungsreduktion Space(0) • NP-schwierig • Pumping-Lemma, Myhill-Nerode • NP-vollständig Ø Berechenbarkeitstheorie • SAT, 3 -SAT, Clique, Subset– Abzählbar Sum, Hamiltonian • Diagonalisierung • Approximationsalgorithmen – Rekursiv Aufzählbar = Akzeptor – NSPACE(S(n)) • Rekursiv Ko-Aufzählbar • SPACE(S(n)2) Satz von Savitch • Diagonalisierung, Abbildungsreduktion – PSPACE – Rekursiv = Entscheidbar • PSPACE-schwierig • Diagonalisierung, Abbildungsreduktion, Turing-Reduktion • PSPACE-vollständig – Beschreibungskomplexität • QBF • Unkomprimierbarkeit von Worten Informatik III 28. Vorlesung - 19

Ende der 28. Vorlesung Albert-Ludwigs-Universität Freiburg Rechnernetze und Telematik Prof. Dr. Christian Schindelhauer Arne Vater Wintersemester 2006/07 28. Vorlesung 09. 02. 2007 20