Inflationary Universe A possible solution to the horizon

Inflationary Universe: A possible solution to the horizon and flatness problems. Alan H. Guth 1981 Sudeep Das “Greatest Hits” Seminar 2004 October 11,

Plan of the Talk • Rush through Big Bang Cosmology… • And stumble upon • Flatness , Horizon & Monopole Problems. � • Enter Guth… • Inflation can solve these problems, • But it raises others… • New Inflation • Chaotic Inflation • Conclusions and Comments.

The Standard Model of the Very Assume that the Universe is homogenous and isotropic, and therefore described by the Robertson-Walker Metric: where k =+1, -1 or 0 for a closed, open and flat and an energy-momentum tensor: I am assuming the speed of light c=1

The Standard Model of the Very With these, the Einstein’s Equations governing the universe become: Freidman Eq where, is the Hubble parameter. At any time, one can define a critical density

The Standard Model of the Very With the equation of state taken as: where w = 1/3 for relativistic particles. w= for NR matter. and for a Cosmological Constant , We get, for a flat universe the following behav The early universe was radiation dominated.

The Standard Model of the Very Thermodynamics of the ultra-relativistic plasm plas Number density: The entropy density is defined as: Where,

The Standard Model of the Very Thermodynamics of the ultra-relativistic plasm plas Number density: The entropy density is defined as: and the following entropy conservation is as a implying For T>>m, so that g(T) is a constant, we ge

The Standard Model of the Very Since , one can trade T for a in the Freid In terms of T , the first of these, i. e. becomes where, with which is conserved.

The Puzzles: Flatness Probl Consider the Friedmann Eqn: WMAP results give =1. 02+/-0. 02 today. Since, in the radiation or matter dominated positi e ve Hence, So, and can only increase with time and hence has to be stupendously

The Puzzles: Flatness Probl Guth takes, today. He gets today. Since, S is assumed conserved, its value at early times can be estimated by its value today. Since, the bound on a lead

The Puzzles: So, Flatness Probl 1. 2. Giving, and Taking One gets, So, by demanding to be within an order of m we find ������ that has to be exceedi

The Puzzles: Horizon Proble Particle Horizon or Physical Horizon: Physical distance that light can travel starting from Big Bang ( t = 0 ). Consider ray of light traveling radially in Since, lighta travels along null geodesics: a flat universe. So, the coordinate distance traversed in time t The physical horizon distance is, therefore, Since , this turns out to be

The Puzzles: Horizon Proble One can see the Horizon Problem vividly by considering the isotropy of the cosmic microwave At decoupling the background. comoving distance over which casual interactions occur is 180 h-1 Mpc. (subtends about 1 degree on the sky today). This is much less than the comoving distance How could these patches know that they had to b

The Puzzles: Horizon Proble So, size of the region in causal contact at time Compare this with the size L(t) of a region that grows into our observable universe. Using conservation of entropy, We can take The ratio of the volumes is, Again with Meaning 10 83 causally disco regions. Yet homogenous? H

The Puzzles: Monopole Pro If Grand Unification occurs with a simple guage group, any spontaneous breaking of the symmetry down to the Standard Model will lead to magnetic monopoles. T�he expected relic abundance of monopoles works out be, This is far too big. Greater by 14 orders of magnitude than observational constraints There are other unwanted model-depende

A clue to the Solutions A crucial assumption that led us to the flatness and horizon problems was the conservation of entropy S. What if that was grossly wrong? What if ?

A clue to the Solutions: Flatness In establishing the Flatness Problem, we Which gave: Eventually giving, To obviate the flatness problem one needs

A clue to the Solutions: Horizon P For the Horizon Problem we estimated the length that grows into the scale of the observed universe as: The length scale in causal contact (horizon) was leading to: So, the horizon problem can be obviated if

Good ! But how does it work? How do we get such a huge entropy multi • A first order phase transition in the Early Universe. • Nucleation rate of new phase<< expansion rate. • Universe supercools below the critical temperature Tc to a much lower temperature Ts , whence the transition takes place. • Latent heat is released, and temperature goes up again to Tr ~ Tc

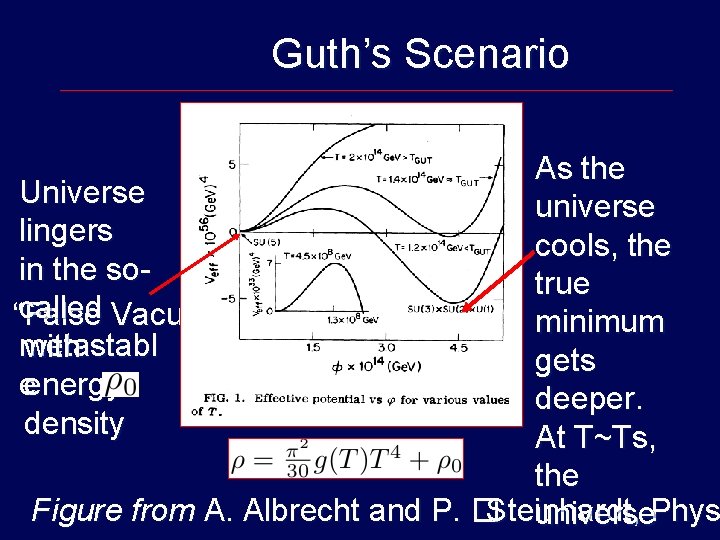
Guth’s Scenario As the Universe universe lingers cools, the in the sotrue called Vacuum” “False minimum metastabl with gets eenergy deeper. density At T~Ts, the Figure from A. Albrecht and P. �Steinhardt, universe. Phys

What is inflating here? Of course, entropy inflates…but wait… Consider again the old Freidmann Equation, but with the new energy density. As the universe, supercools the 2 nd and 3 rd te which has soln. , with This implies an exponentially inflating scale fa

What is inflating here? We should be able to see this behavior directly Stress-energy tensor for the “false vacuum” is: This makes the Friedmann Eqn. :

Changing the point of view We saw that Guth attacked the problem from the entropy point of view. What if, we forget all about phase transitions and entropy and ask: If we somehow create an accelerated expansion, will the problems of Big Bang theory be solved? The answer is, as it should be, yes.

Changing the point of view: Flatne Define Inflation to be an epoch with Recall that flatness problem emerged from the increasing nature of the RHS of: However, during inflation, so that even if started from a value away it can be brought sufficiently close to zero by Flatness problem does not arise.

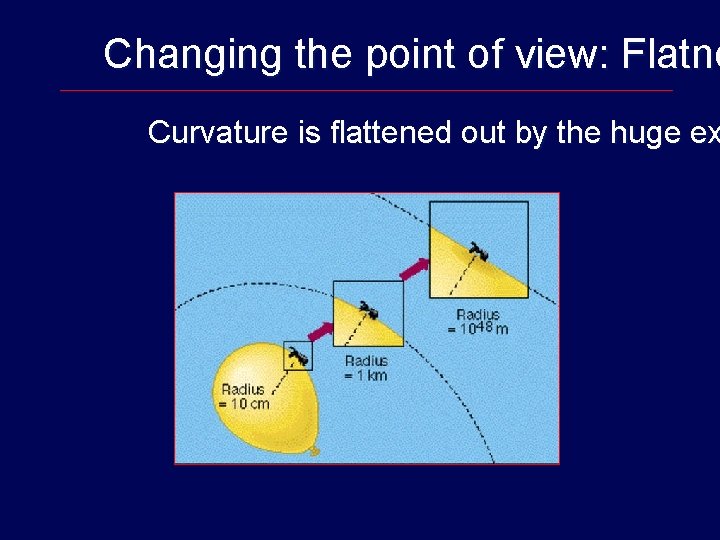
Changing the point of view: Flatne Curvature is flattened out by the huge ex

Changing the point of view: Horizo Horiz The physical horizon was shown to be, The comoving horizon is 1/(a H) and is a decreasing function of time during inflation. Therefore, the comoving horizon shrinks durin

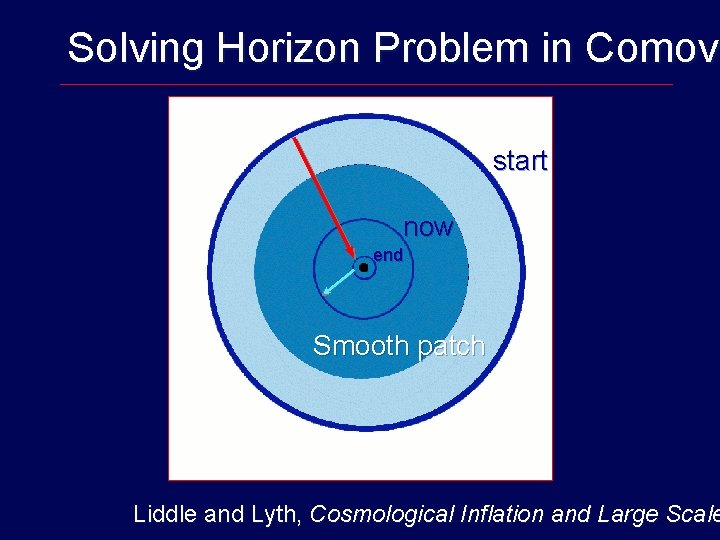
Solving Horizon Problem in Comovi Comov start now end Smooth patch Liddle and Lyth, Cosmological Inflation and Large Scale

Inflation in the Abstract Inflation is an add-on to the standard Big Ban Following equivalent descriptions hold: An era of accelerated expansion, An era of shrinking horizon, An era of a non-standard equation of state,

What went wrong with Guth’s T Guth’s phase transition scenario surely conforms to these requirements. was a serious problem. • But The there bubbles of true vacuum will form at various times in various places in the false vacuum. • They will have great difficulty merging because the space separating them will still be expanding exponentially. • The. Guth phase&transition will(1983) Weinberg

What came after Guth’s Theory • New Inflation (Linde 1982, Albrecht & Steinhardt 1982): Roll down a flat potent • Chaotic Inflation (Linde 1983) Slide through a viscous medium.

New Inflation Linde (1982), Albrecht and Steinhardt (1982). Still a phase transition. Most of the interesting part of inflation takes place away from the false vacuum. The field rolls down slowly. Space inside bubbles of expand One bubble can grow to anew sizephase ~ 103000 cm >> scale The whole universeexponentially. can be accommodated in

Chaotic Inflation (Linde 1983 Chaotic Inflation can occur even with simplest fo f The equation of motion for the field has a “drag” term due to expansion of the universe, This term slows down the velocity of the field. If , the equation of state is tha

Chaotic Inflation Simple!! No supercooling/tunneli ng from false vacuum. No plateau. No thermal equilibrium! Initial Universe may be thought In 10 -35 ofs, asa having Plank chaotically distributed values field. blows Inflation sizeof region up took where was large. At theplace end ofonly inflation, the field oscillates and to~ ���� decays into particle-pairs, which and cmsinteract ! thermalize at some temperature. Standard Big

Eternal Inflation Quantum Fluctuations can “kick the rolling ball back up the hill” at some points. These regions expand faster than the parent regions. In many points within this region, the expansion decays into standard big bang evolution (universes as our own), quantum fluctuations again causes some otherturn out to Essentially all inflationary models point to inflate even faster. This process Still not goes onfully andunderstood on and the !Universe reproduces itself.

Conclusion & Further Commen • The inflationary paradigm is essential in theory of cosmic evolution because it is a single class of theories which consistently answers, • Why is the Universe so flat? • Why is the Universe so homogenous and isotropic? • Why aren’t there any magnetic monopoles? • How did the Hubble Expansion start? • How do the density perturbations and anisotropies in the CMB appear? . Scale invariance. (Katie’s Talk!!) • Guth’s 1981 paper is important because inflation was invented in it. • So far, observations have been consistent with