Infinitely small values Programming with Infinitesimals A WHILELanguage

Infinitely small values Programming with Infinitesimals A WHILE-Language for Hybrid System Modeling Kohei Suenaga JSPS Research Fellow (PD) Kyoto University Ichiro Hasuo University of Tokyo

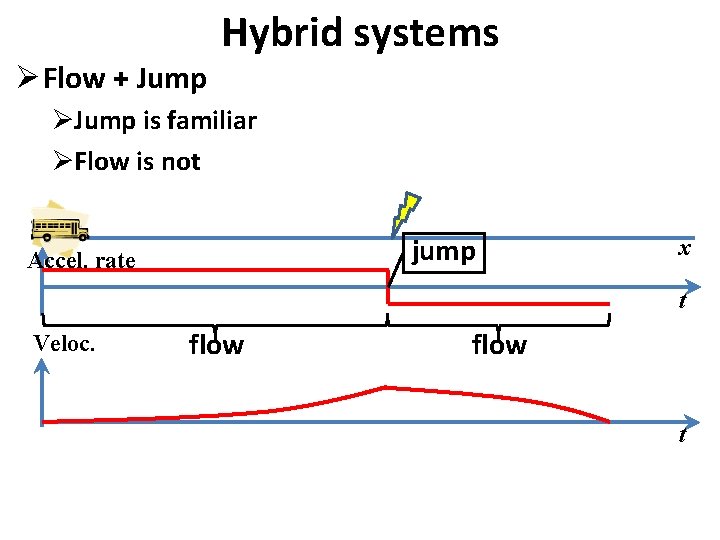
Ø Flow + Jump Hybrid systems ØJump is familiar ØFlow is not jump Accel. rate x t Veloc. flow t

Hybrid System Verification Ø Existing work ØHybrid automata [Alur et al. ] ØDifferential dynamic logic [Platzer et al. ] Ø Flow by differential equations

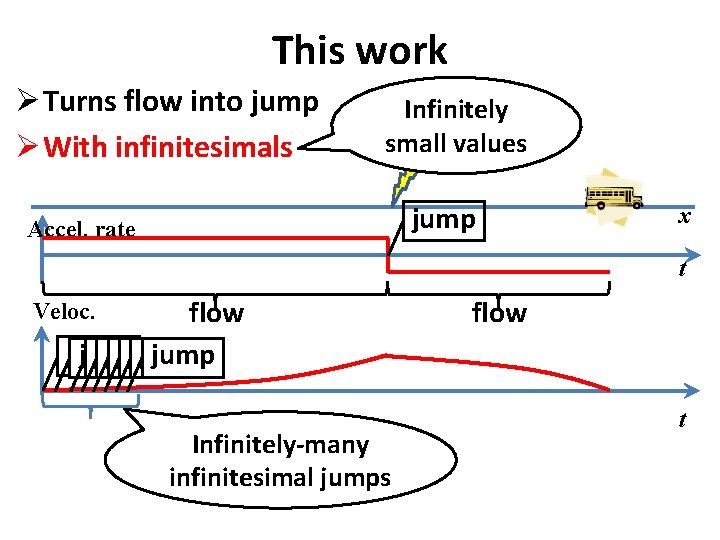
This work Ø Turns flow into jump

This work Ø Turns flow into jump Ø With infinitesimals Infinitely small values

This work Ø Turns flow into jump Ø With infinitesimals Infinitely small values jump Accel. rate x t flow jump jump Veloc. Infinitely-many infinitesimal jumps flow t

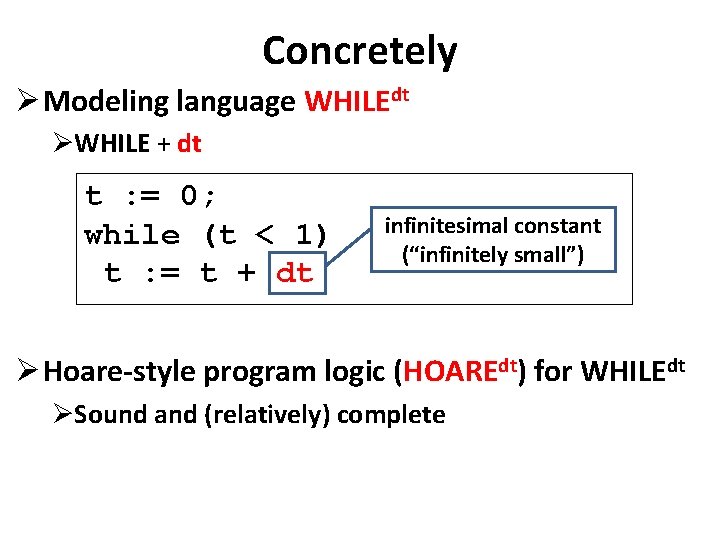
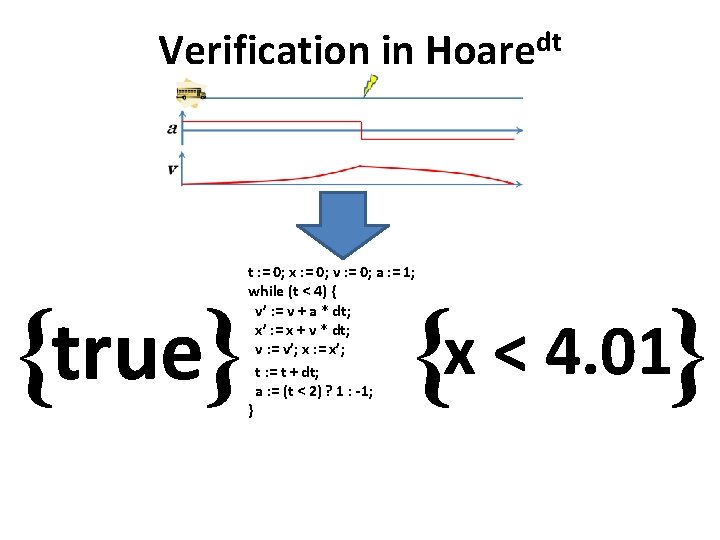
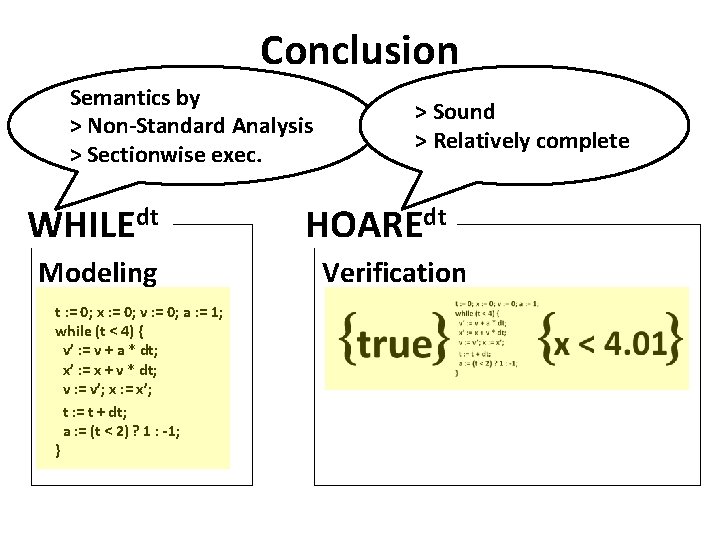
Concretely Ø Modeling language WHILEdt ØWHILE + dt t : = 0; while (t < 1) t : = t + dt infinitesimal constant (“infinitely small”) Ø Hoare-style program logic (HOAREdt) for WHILEdt ØSound and (relatively) complete

Verification in { A } dt Hoare c { B }

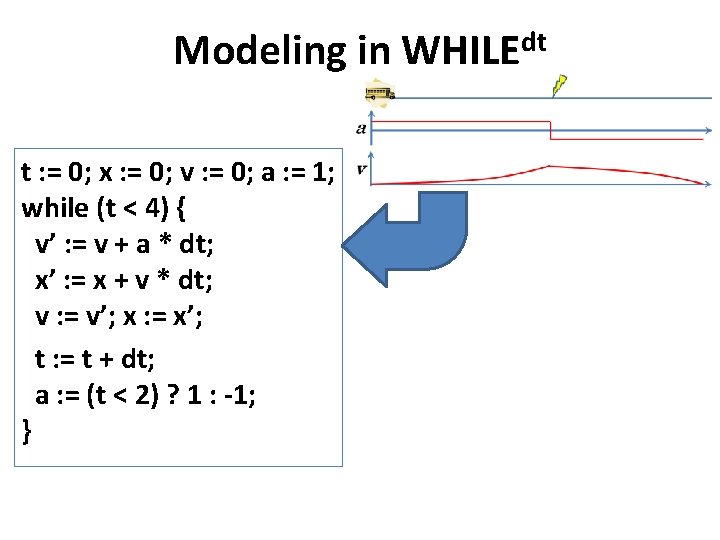
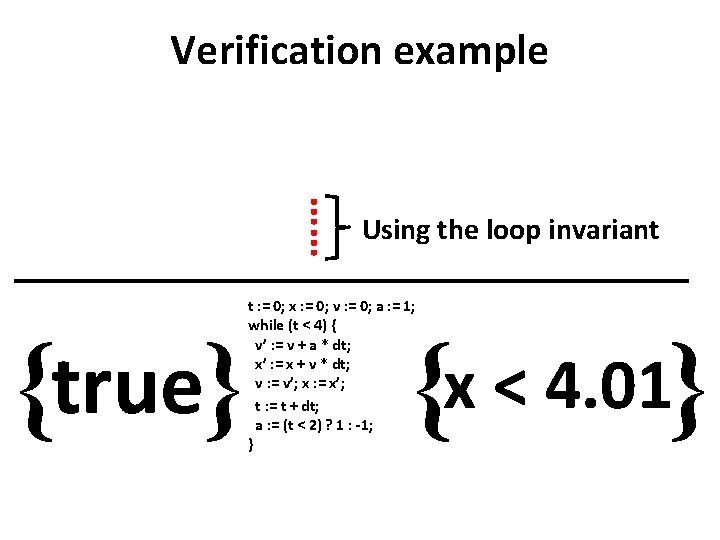
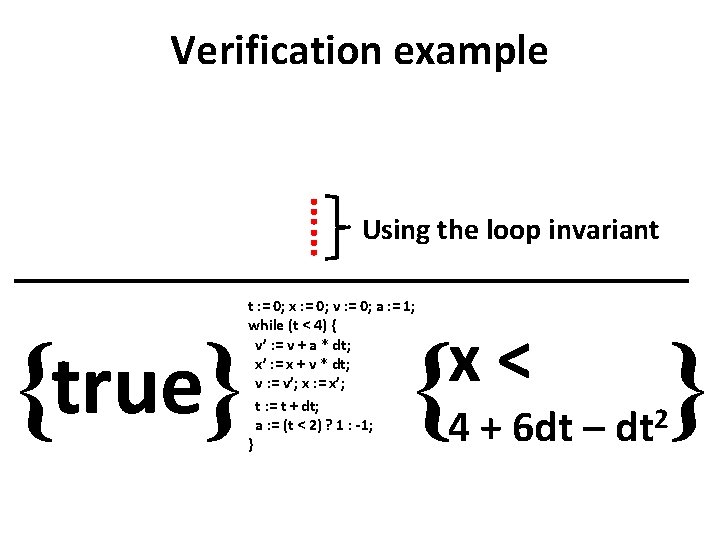
Verification in {true} t : = 0; x : = 0; v : = 0; a : = 1; while (t < 4) { v’ : = v + a * dt; x’ : = x + v * dt; v : = v’; x : = x’; t : = t + dt; a : = (t < 2) ? 1 : -1; } dt Hoare {x < 4. 01}

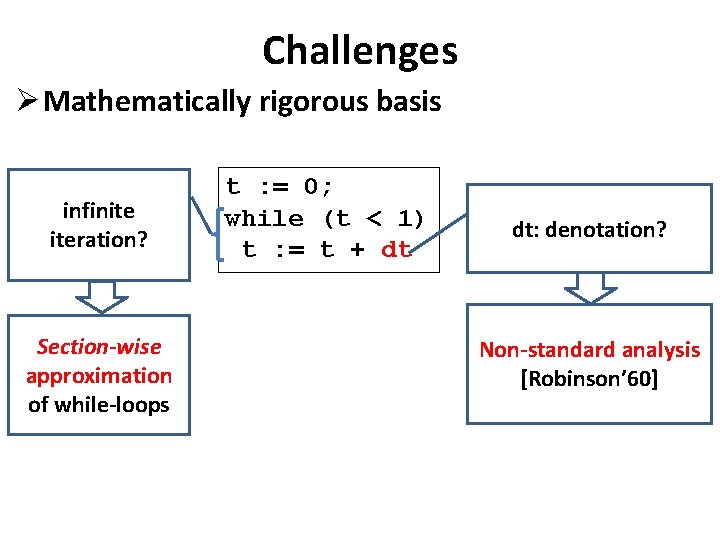
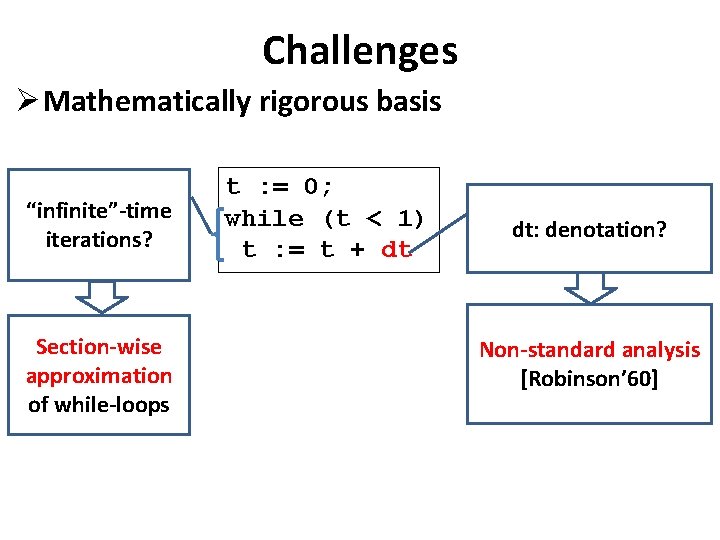
Challenges Ø Mathematically rigorous basis infinite iteration? Section-wise approximation of while-loops t : = 0; while (t < 1) t : = t + dt dt: denotation? Non-standard analysis [Robinson’ 60]

Outline Ø WHILEdt ØSyntax and example ØBrief introduction of non-standard analysis ØSemantics Ø HOAREdt Ø Related work Ø Conclusion

Ø WHILE + reals + dt dt WHILE infinitesimal real a : : = x | r | dt | a 1+a 2 | … b : : = true | false | b 1 and b 2 | b 1 or b 2 | not b c (commands) : : = (inaction) skip (assignment) | x : = a (sequential) | c 1; c 2 | if (b) then c 1 else c 2 (conditional) (loop) | while (b) do c

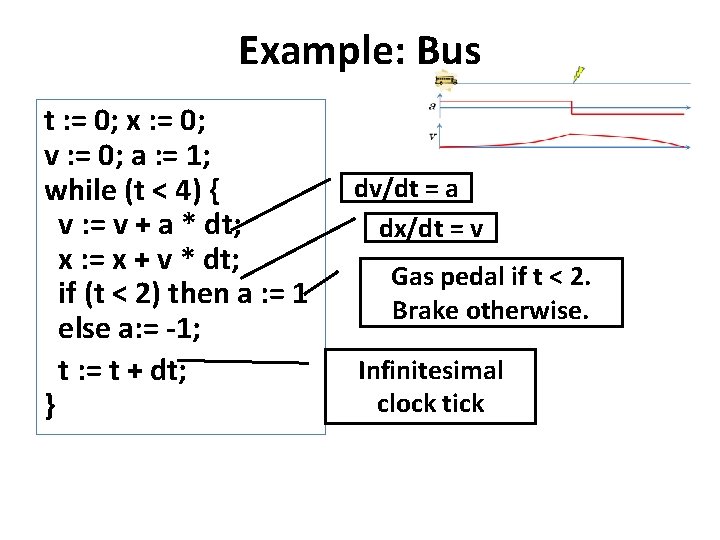
Example: Bus t : = 0; x : = 0; v : = 0; a : = 1; while (t < 4) { v : = v + a * dt; x : = x + v * dt; if (t < 2) then a : = 1 else a: = -1; t : = t + dt; } dv/dt = a dx/dt = v Gas pedal if t < 2. Brake otherwise. Infinitesimal clock tick

Challenges Ø Mathematically rigorous basis “infinite”-time iterations? Section-wise approximation of while-loops t : = 0; while (t < 1) t : = t + dt dt: denotation? Non-standard analysis [Robinson’ 60]

Outline Ø WHILEdt ØSyntax and sample programs ØBrief introduction of non-standard analysis ØSemantics Ø HOAREdt Ø Answer to FAQs Ø Conclusion

Non-standard analysis in nutshell Ø Hyperreal ≒ sequence of reals ( ) Reals + dt Ø Operations: Pointwise + = ( ( Ø Predicates: Pointwise “almost everywhere” ) )

Hyperreal ≒ sequence of reals (1, 1, …) (1, 2, 3, 4, …) ( ) Ø A component of a sequence is called a section (1, 2, 3, 4, …) 0 th section 2 nd section NB. Precisely, Hyperreal = (sequence of reals) / ultrafilter

Real as hyperreal Ø Reals are naturally embedded to hyperreals Real Hyperreal 1 (1, 1, …) 2 (2, 2, …) p (p, p, …)

Operations: Sectionwise ) ( + ) ( =

Predicates: Sectionwise “almost everywhere” Ø Predicate holds if it holds except for finitely-many sections < < < ? ✓ (0, 0, …) … (1, 2, 3, 4, …)

Predicates: Sectionwise “almost everywhere” Ø Predicate holds if it holds except for finitely-many sections < < < ? ✓ (1, 1, …) … (1, 2, 3, 4, …)

Predicates: Sectionwise “almost everywhere” Ø Predicate holds if it holds except for finitely-many sections < < < ? (1, 2, 3, 4, …) … (0, 1, 2, 3, …) (NB “almost every section” is defined with an ultrafilter in the paper)

dt = ( ) is an infinitesimal Ø Infinitesimal = Smaller than any positive real < … < ? ( ✓ ) < < < ( … )

Outline Ø WHILEdt ØSyntax and sample programs ØBrief introduction of non-standard analysis ØSemantics Ø HOAREdt Ø Answer to FAQs Ø Conclusion

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = 0; while (t < 1) t : = t + dt;

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = 0; while (t < 1) t : = t + dt;

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = (0, 0, 0, …); while (t < (1, 1, 1, …)) t : = t + (1, 1/2, 1/3, …);

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result 0 th section 1 st section 2 nd section t : = 0; while (t < 1) t : = t + 1; t : = 0; while (t < 1) t : = t + 1/2; t : = 0; while (t < 1) t : = t + 1/3; …

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result 0 th section 1 st section 2 nd section t : = 0; while (t < 1) t : = t + 1; t : = 0; while (t < 1) t : = t + 1/2; t : = 0; while (t < 1) t : = t + 1/3; t=1 t=1 …

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = (0, 0, 0, …); while (t < (1, 1, 1, …)) t : = t + (1, 1/2, 1/3, …); t = (1, 1, 1, …)

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = 0; while (t < 1) t : = t + dt; t=1

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = 0; while (t <= 1) t : = t + dt;

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = 0; while (t <= 1) t : = t + dt;

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = (0, 0, 0, …); while (t <= (1, 1, 1, …)) t : = t + (1, 1/2, 1/3, …);

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result 0 th section 1 st section 2 nd section t : = 0; while (t <= 1) t : = t + 1; t : = 0; while (t <= 1) t : = t + 1/2; t : = 0; while (t <= 1) t : = t + 1/3; …

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result 0 th section 1 st section 2 nd section t : = 0; while (t <= 1) t : = t + 1; t : = 0; while (t <= 1) t : = t + 1/2; t : = 0; while (t <= 1) t : = t + 1/3; t=1+1 t = 1 + 1/2 t = 1 + 1/3 …

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = (0, 0, 0, …); while (t <= (1, 1, 1, …)) t : = t + (1, 1/2, 1/3, …); t = (1, 1, 1, …) + (1, 1/2, 1/3, …)

Idea of the semantics Ø Section-wise execution ØExecute a program on each section and merge the result t : = 0; while (t <= 1) t : = t + dt; t = 1 + dt

Sectionwise Execution Lemma Ø Def. (Section) The i-th section e|i of a WHILEdt expression e is obtained by Usual program, replacing dt with usual semantics Ø Lem. (Sectionwise Execution) For each program c and a memory state s, stores hyperreals stores reals

Q: Is dt WHILE program executable? Ø A: No ØWHILEdt is for modeling and verification of hybrid systems

Outline Ø WHILEdt Ø HOAREdt Ø Related work Ø Conclusion

Assertion language Ø Almost the same as the standard Hoare logic Set of hypernaturals A (assertion) : : = true | false | A 1 and A 2 | not A | a 1 < a 2 | ∀x∈*N. A |∀x∈*R. A Set of hyperreals Ø Cf. Transfer Principle in Non-Standard Analysis

Hoare triples and inference rules Ø Exactly the same as the standard Hoare logic {A}skip{A} {A 1}c 1{A 2}c 1{A 3} {A 1}c 1; c 2{A 3} {[a/x]A}x : = a{A} {A 1 and b}c 1{A 2} {A 2 and not b}c 2{A 2} {A 1}if b then c 1 else c 2{A 2} {A and b}c{A} {A}while b do c{A and not b}

Verification example t : = 0; x : = 0; Loop invariant: v : = 0; a : = 1; ∃n∈*N. t = n * dt & while (t < 4) { t < 2 + dt v’ : = v + a * dt; v = n * dt & a = 1 & x’ : = x + v * dt; x = (n-1)n*dt 2 / 2 v : = v’; x : = x’; t >= 2 + dt if (t < 2) then a : = 1 v = (2 n 0 + 4 – n) * dt & else a: = -1; a = -1 & t : = t + dt; x = x 0 + (3 n 0 + 7 – n)(n – n 0 - 2)*dt 2 / 2 }

Verification example t : = 0; x : = 0; Loop invariant: v : = 0; a : = 1; ∃n∈*N. t = n * dt & while (t < 4) { t < 2 + dt v’ : = v + a * dt; v = n * dt & a = 1 & x’ : = x + v * dt; x = (n-1)n*dt 2 / 2 v : = v’; x : = x’; t >= 2 + dt if (t < 2) then a : = 1 v = (2 n 0 + 4 – n) * dt & else a: = -1; a = -1 & t : = t + dt; x = x 0 + (3 n 0 + 7 – n)(n – n 0 - 2)*dt 2 / 2 }

Verification example t : = 0; x : = 0; Loop invariant: v : = 0; a : = 1; ∃n∈*N. t = n * dt & while (t < 4) { t < 2 + dt v’ : = v + a * dt; v = n * dt & a = 1 & x’ : = x + v * dt; x = (n-1)n*dt 2 / 2 v : = v’; x : = x’; t >= 2 + dt if (t < 2) then a : = 1 v = (2 n 0 + 4 – n) * dt & else a: = -1; a = -1 & t : = t + dt; x = x 0 + (3 n 0 + 7 – n)(n – n 0 - 2)*dt 2 / 2 }

Verification example …… {true} Using the loop invariant t : = 0; x : = 0; v : = 0; a : = 1; while (t < 4) { v’ : = v + a * dt; x’ : = x + v * dt; v : = v’; x : = x’; t : = t + dt; a : = (t < 2) ? 1 : -1; } {x < 4. 01}

Properties Thm. HOAREdt is sound Thm. HOAREdt is relatively complete

Related work Ø Hybrid automata [Alur et al. ] ØExtension of automata with diff. eqn. ØSupports concurrency ØAutomated verification Ø Differential dynamic logic [Platzer et al. ] ØExtension of dynamic logic with diff. eqn. ØSound & relatively complete ØAutomated verification

Conclusion Semantics by > Non-Standard Analysis > Sectionwise exec. WHILEdt Modeling t : = 0; x : = 0; v : = 0; a : = 1; while (t < 4) { v’ : = v + a * dt; x’ : = x + v * dt; v : = v’; x : = x’; t : = t + dt; a : = (t < 2) ? 1 : -1; } > Sound > Relatively complete HOAREdt Verification

Future direction Ø Verifier based on this approach ØCurrent prototype: WHILEdt w/ invariants Verif. cond. Coq ØAutomated verification? ØMeti. Tarski ØInvariant generators Ø Application of other software verification methods Ø Extension of the language Ø Feasibility study with more examples

Does the choice of dt matter? Ø A: Yes t : = 0; while (t = 1) t : = t + dt; Terminates with dt = (1, 1/2, 1/3, …) Doesn’t with dt = (1/p, 1/2 p, 1/3 p, …)

Zeno behavior Ø Problematic? No ØThere is no special notion of “time” ØVariable “t” in the examples is just a variable ØProgression of t is not required by the framework ØProving “progress” of a variable is an interesting future direction

Verification example …… {true} Using the loop invariant t : = 0; x : = 0; v : = 0; a : = 1; while (t < 4) { v’ : = v + a * dt; x’ : = x + v * dt; v : = v’; x : = x’; t : = t + dt; a : = (t < 2) ? 1 : -1; } x< { 4 + 6 dt – } dt 2