InfGraph Draw Automatic Graph Drawing Lecture 2 Terminology

Inf-Graph. Draw: Automatic Graph Drawing Lecture 2 Terminology Reinhard von Hanxleden rvh@informatik. uni-kiel. de Most definitions are from [Di Battista Book 99]. This lecture is based in part on material kindly provided by Bettina Speckmann. 1

Basics • Graph: pair G = (V, E) • Vertices (Nodes): set V = {v 1, …, vn } • Edge (link, arc, connection): unordered pair e = (u, v) ∈ V×V • Edges: set E = {e 1, …, en } • Sometimes allow E to be multi-set (bag) i. e. , a set that allows multiple instances of its elements • Multiple edge (or multi edge): edge that occurs more than once in E 2

Edges • Self-loop: edge (u, u) ∈ V×V • Simple graph: graph without self-loops and multiple edges • Default: assume that graphs are simple • Extension: hyper edges that connect an arbitrary number of vertices / ports 3

Edges For an edge e = (u, v): • End vertices of e: u and v • u and v are adjacent to each other • e is incident to u and v 4

Neighbors • Neighbors of v, denoted δ(v), are its adjacent vertices • Degree of v, denoted ∆(v), is the number of its incident edges (which for simple graphs is the number of its neighbors) 5

Digraphs • Directed Graph (digraph): E is set of directed edges • Directed edge: ordered pair e = (u, v) ∈ V×V • e is outgoing edge of u, incoming edge of v • Source: vertex without incoming edge • Sink: vertex without outgoing edge • Indegree / Outdegree of v: number of its incoming/outgoing edges 6

Paths • (Directed) path of length n of (directed) graph G = (V, E): sequence (v 1, …, vn) of vertices in G, (vi, vi+1) ∈ E for 1 ≤ i < n • Simple (directed) path: (directed) path in which all vertices are distinct 7

Cycles • (Directed) cycle: (directed) path with vn = v 1 • Triangle: cycle of length 3 • Hamiltonian cycle/path (spanning cycle/path): cycle/path that visits each vertex in G exactly once • (Directed) graph is acyclic iff it does not contain any (directed) cycles 8

Notes on Paths • Most definitions of path require paths to be simple, we here assume this by default as well; this excludes cycles • [Di Battista Book 99] requires the vertices in a path to be distinct (as required here for a simple path) and defines a cycle as a path with (vn, v 1) ∈ E. However, if (vn, v 1) ∈ E, this definition precludes to distinguish notationally a path that begins in v 1 and ends in vn from a cycle that begins in v 1 and ends in v 1. • Some definitions of path explicitly include the involved edges as well. The above definition, based on [Di Battista Book 99] with the above modification, includes the edges implicitly. This simplifies the definition and works for our standard assumption of graphs being simple. However, if we allow multiple edges, a path must also include the edges to be fully determined. 9

Paths vs. Walks Some sources also distinguish walks and paths. Quoting wikipedia: A walk is an alternating sequence of vertices and edges, starting and ending at a vertex, in which each edge is adjacent in the sequence to its two endpoints. In a directed graph the ordering of the endpoints of each edge in the sequence must be consistent with the direction of the edge. Some sources call walks paths, while others reserve the term "path" for a simple path (a walk without repeated vertices or edges). Walks are also sometimes called chains. A walk is open if its starts and ends at two different vertices, and closed if it starts and ends at the same vertex. A closed walk may also be called a cycle. Alternatively, the word "cycle" may be reserved for a simple closed walk (one without repeated vertices or edges except for the repetition of the starting and final vertex). A walk without repeated edges (but with vertex repetition allowed) may be called a trail and a closed trail may be called a tour. In the context of ear decomposition, a walk that can have the same starting and ending vertex but otherwise avoids any repeated vertices may be called an ear. [https: //en. wikipedia. org/wiki/Glossary_of_graph_theory#walk] 10

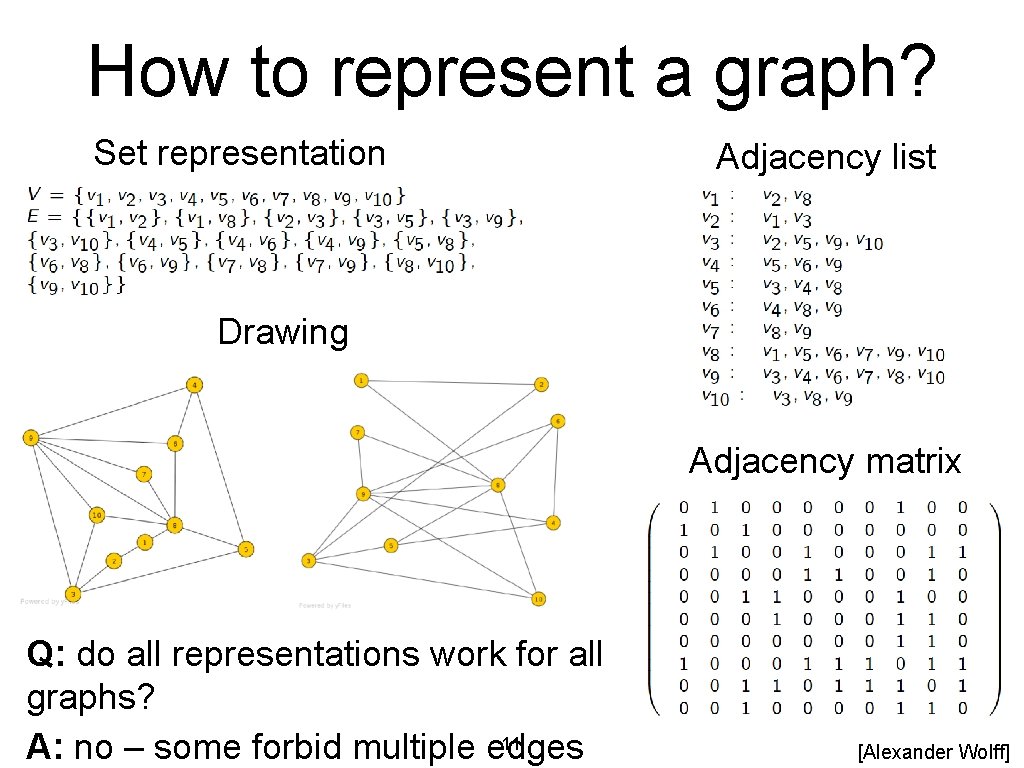
How to represent a graph? Set representation Adjacency list Drawing Adjacency matrix Q: do all representations work for all graphs? 11 A: no – some forbid multiple edges [Alexander Wolff]

Curves • Plane: 2 -dimensional surface that extends infinitely far (1 -d: line, 0 -d: point) • Curve: subset of ℝ 2 of the form α = { γ(x) : x ∈ [0, 1]}, where γ : [0, 1] → ℝ 2 is continuous mapping from closed interval [0, 1] to the plane. γ(0) and γ(1) are the endpoints of curve α. • A curve is closed if its first and last points are the same, otherwise it is open. • A curve is simple if it has no repeated points except possibly first = last. 12

Drawings • Drawing (Layout) Γ of a graph: Function that maps each vertex v to a point Γ(v) ∈ ℝ×ℝ in a plane and each edge (u, v) to a simple curve Γ(u, v) with endpoints Γ(u) and Γ(v). • Note: [Di Battista Book 99] defines drawings of edges based on simple open Jordan curves, instead of simple curves. However, Jordan curves are typically defined to be closed, and for self loops, that may indeed be desired. • Extension: associate each vertex v with a width wv ∈ ℝ and a height hv ∈ ℝ • Extension: associate each vertex v with ports that are attached to v’s boundaries and that serve as end points for edges 13

Layout • Layout creation: process of adding geometric attributes to a graph, or of creating a drawing of a graph • Layout adjustment: process of changing geometric attributes to adjust, of of adjusting the drawing of a graph 14

Planarity [Bettina Speckmann]

Planarity [Bettina Speckmann]

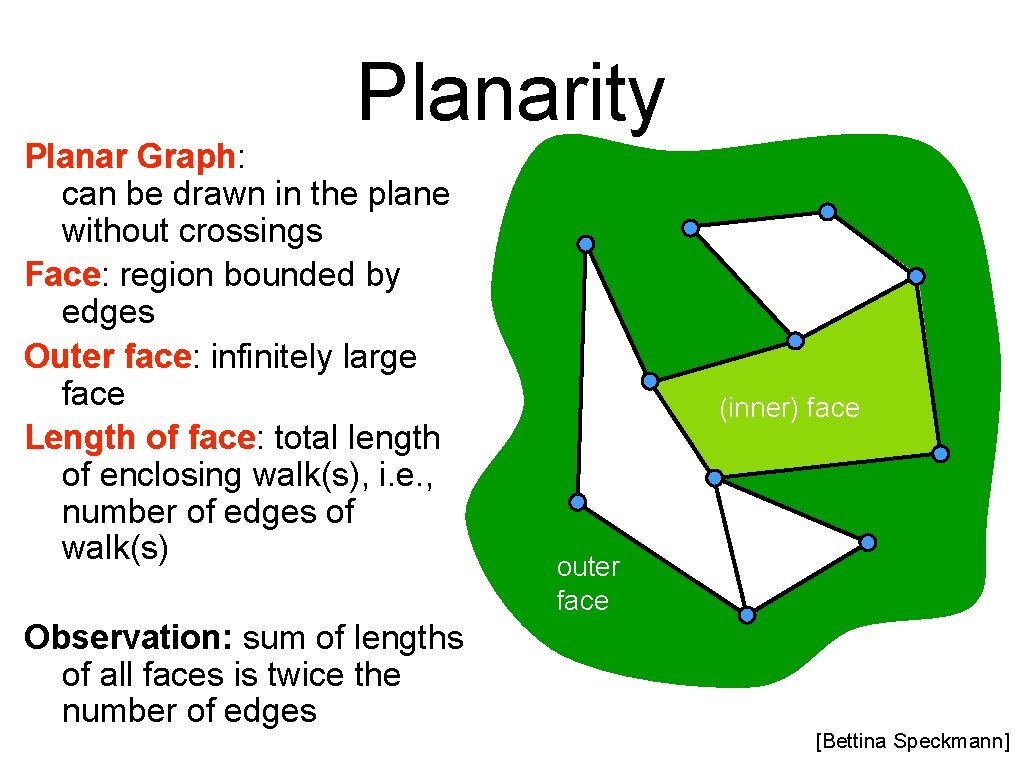
Planarity Planar Graph: can be drawn in the plane without crossings Face: region bounded by edges Outer face: infinitely large face Length of face: total length of enclosing walk(s), i. e. , number of edges of walk(s) Observation: sum of lengths of all faces is twice the number of edges (inner) face outer face [Bettina Speckmann]

Embeddings • Planar drawing determines circular ordering on the neighbors of each vertex v according to clockwise sequence of incident edges around v • Two planar drawings are equivalent: they determine same circular orderings of neighbor sets • (Planar/plane) embedding is equivalence class of planar drawings, described by circular order of neighbors of each vertex • Embedded graph: a graph with a specified embedding Terminology not always used consistently: • Sometimes, a (plane) embedding of G also refers to a planar drawing of G • Sometimes, plane graph also 18 denotes a planar drawing of G

Planarity Plane Graph: planar graph with a fixed embedding [Bettina Speckmann]

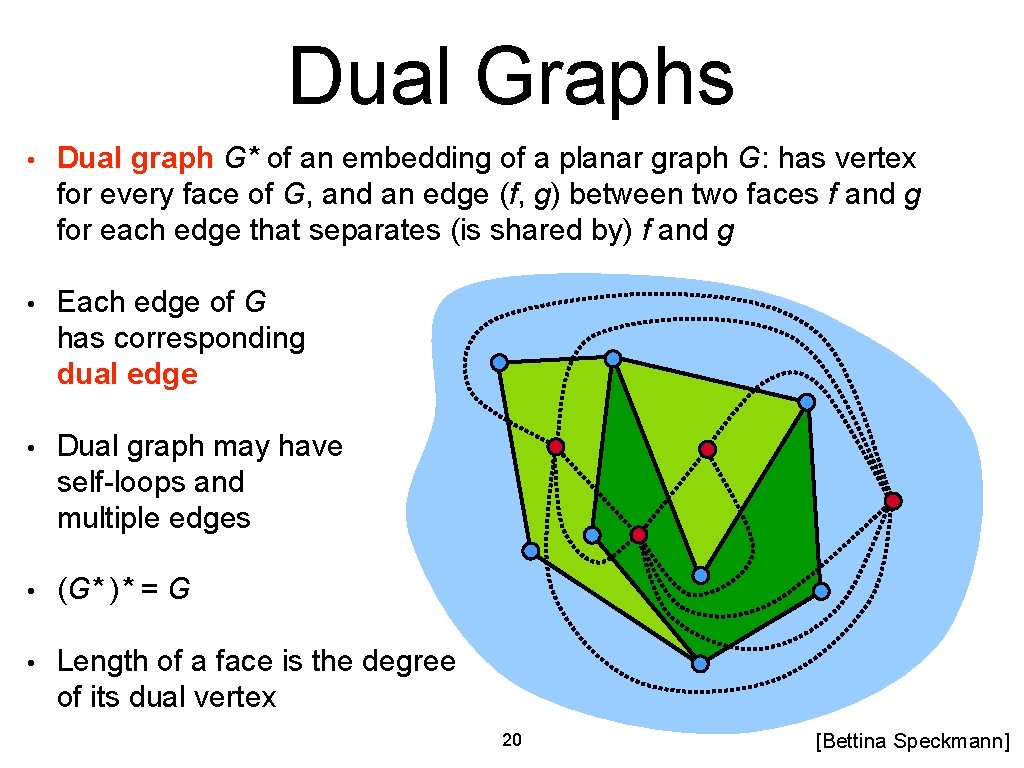
Dual Graphs • Dual graph G* of an embedding of a planar graph G: has vertex for every face of G, and an edge (f, g) between two faces f and g for each edge that separates (is shared by) f and g • Each edge of G has corresponding dual edge • Dual graph may have self-loops and multiple edges • (G* )* = G • Length of a face is the degree of its dual vertex 20 [Bettina Speckmann]

Notes on Planarity • Thm: Two drawings have the same embedding iff they have the same dual graph • We say that two graphs have same topology if they have the same dual graph • We say that a layout adjustment algorithm preserves topology if the adjusted layout has the same topology as the original layout (see also mental map) 21 Jump to Lecture 3

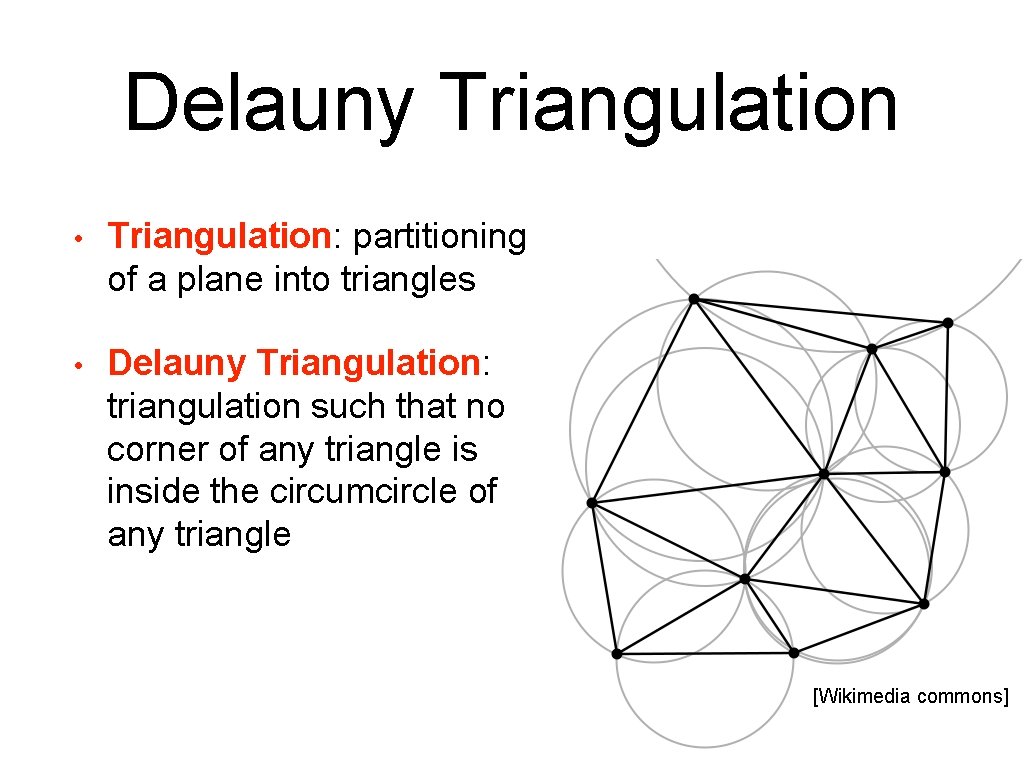
Delauny Triangulation • Triangulation: partitioning of a plane into triangles • Delauny Triangulation: triangulation such that no corner of any triangle is inside the circumcircle of any triangle [Wikimedia commons]

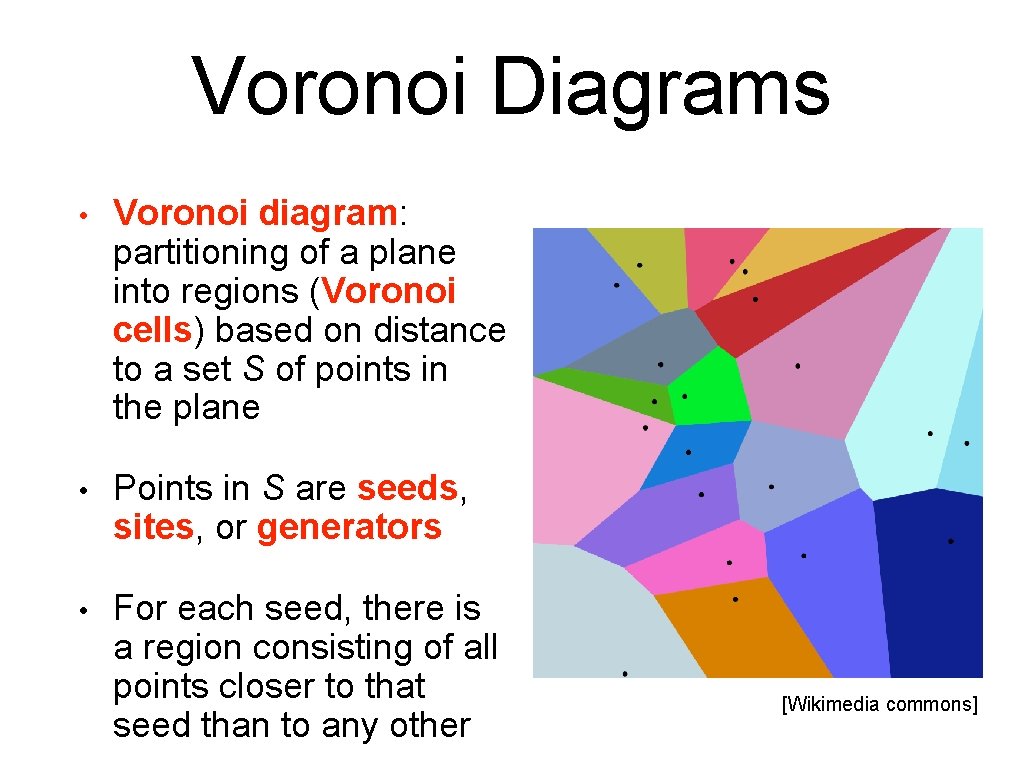
Voronoi Diagrams • Voronoi diagram: partitioning of a plane into regions (Voronoi cells) based on distance to a set S of points in the plane • Points in S are seeds, sites, or generators • For each seed, there is a region consisting of all points closer to that seed than to any other [Wikimedia commons]

Voronoi Diagrams • Voronoi diagram: partitioning of a plane into regions (Voronoi cells) based on distance to a set S of points in the plane • Points in S are seeds, sites, or generators • For each seed, there is a region consisting of all points closer to that seed than to any other [Wikimedia commons]

Voronoi Diagrams are dual to Delauny Triangulations Q: Why does this work? [Wikimedia commons]

Subgraphs G’ = (V’, E’) is subgraph of G = (V, E): V’ ⊆ V and E’ ⊆ E ⋂ (V’ × V’) • G’ is proper subgraph of G: V’ ≠ V or E’ ≠ E • G’ is induced by V’: E’ = E ⋂ (V’ × V’) 26

Connectedness • G is connected: There is a path between each pair of vertices • Connected component of G: maximal connected subgraph of G • Cutvertex (articulation vertex) of graph G: vertex whose removal disconnects G • G is biconnected: G is connected and has no cutvertices • G is separable: G is not biconnected 27

Connectedness • Biconnected components (blocks) of graph G: maximal biconnected subgraphs of G • Thm: Graph is planar iff its blocks are planar [Wikimedia commons] 28

Drawing conventions Drawing convention: basic rule that a drawing must satisfy to be admissible • Planar drawing • Straight-line drawing • Polyline drawing • (Box-)orthogonal drawing • Grid drawing • Visibility drawing • For digraphs only: (strictly) upward/downward drawing 31

Planar drawings Vertices Edges points in the plane curves No edge crossings 32 [Bettina Speckmann]

Straightline drawings Vertices Edges points in the plane straight lines Theorem Every planar graph has a plane embedding where each edge is a straight line. [Wagner 1936, Fáry 1948, Stein 1951] 33 [Bettina Speckmann]

Polygons • Polygon: plane figure that is bounded by a finite chain of straight line segments closing in a loop. Line segment is polygon’s edge/side, meeting point is polygon’s vertex/corner. • Simple polygon: polygon with non-intersecting sides • Convex polygon: simple polygon with all interior angles ≤ 180° • Strictly convex polygon: simple polygon with all interior angles < 180° 34

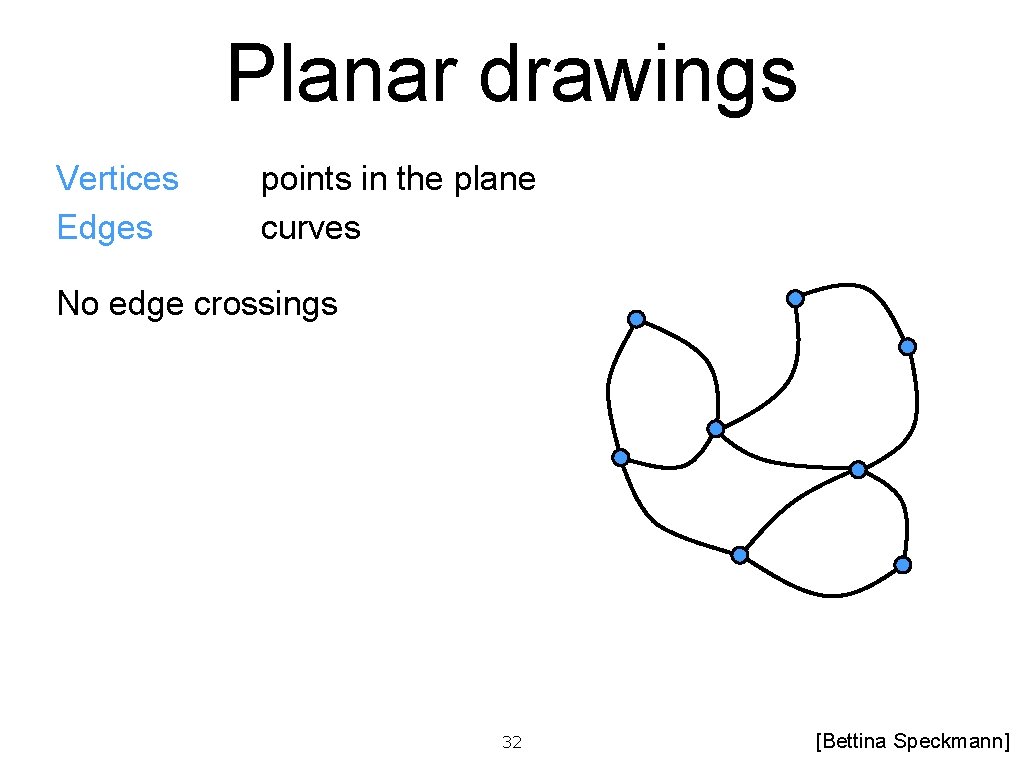
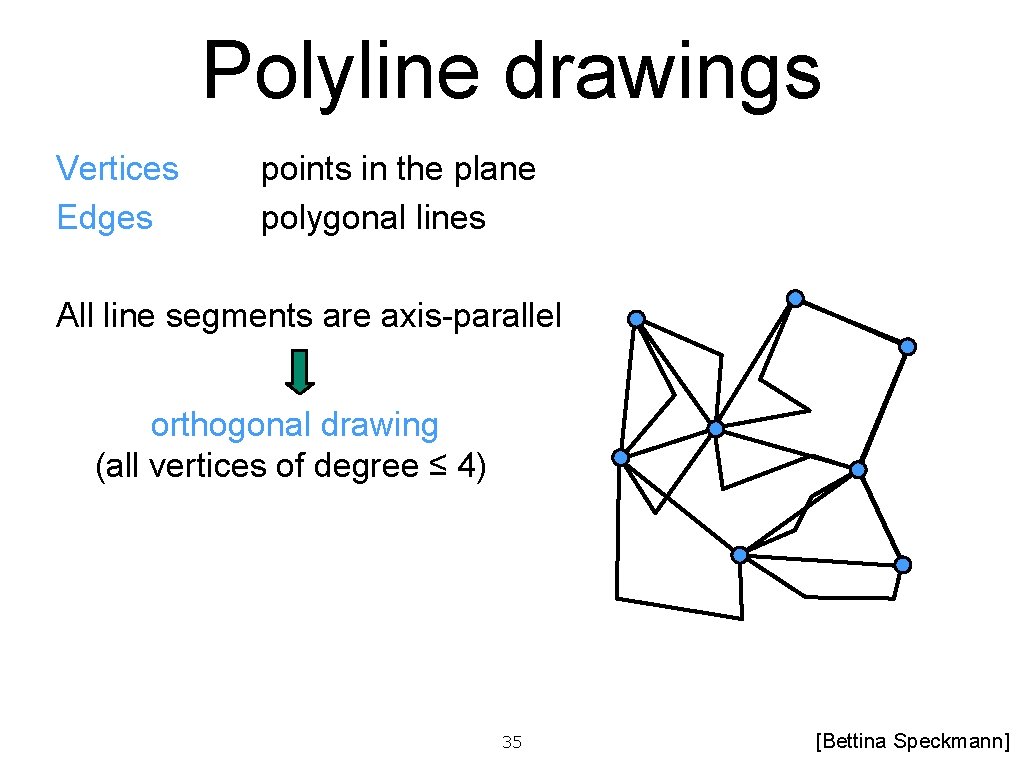
Polyline drawings Vertices Edges points in the plane polygonal lines All line segments are axis-parallel orthogonal drawing (all vertices of degree ≤ 4) 35 [Bettina Speckmann]

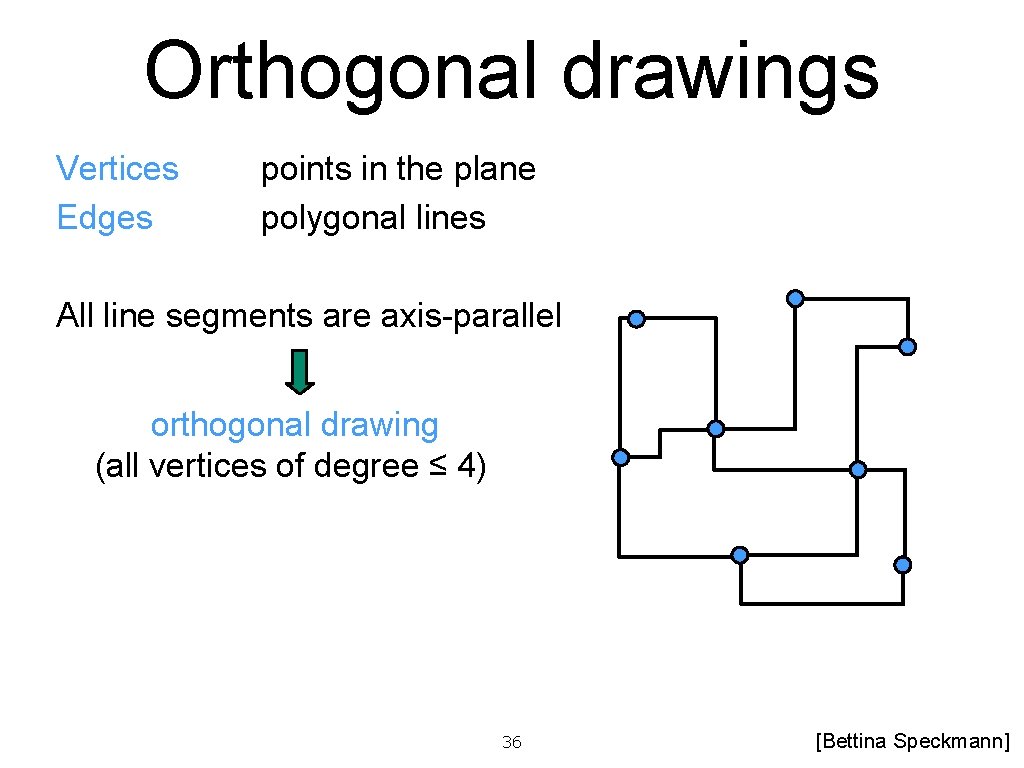
Orthogonal drawings Vertices Edges points in the plane polygonal lines All line segments are axis-parallel orthogonal drawing (all vertices of degree ≤ 4) 36 [Bettina Speckmann]

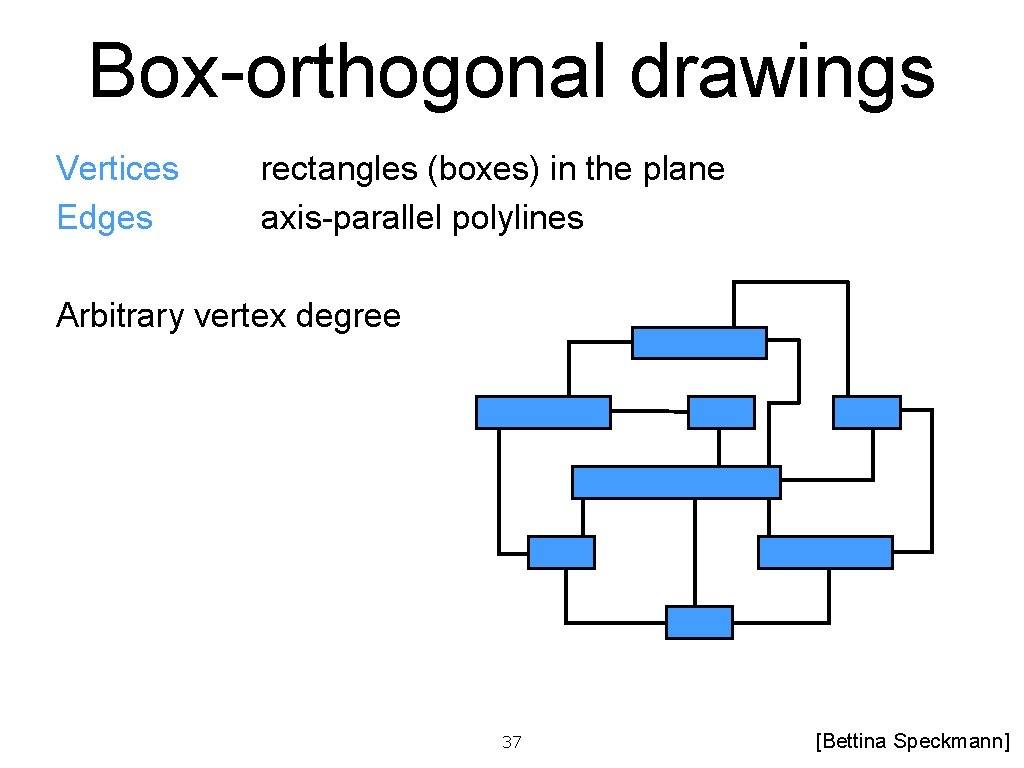
Box-orthogonal drawings Vertices Edges rectangles (boxes) in the plane axis-parallel polylines Arbitrary vertex degree 37 [Bettina Speckmann]

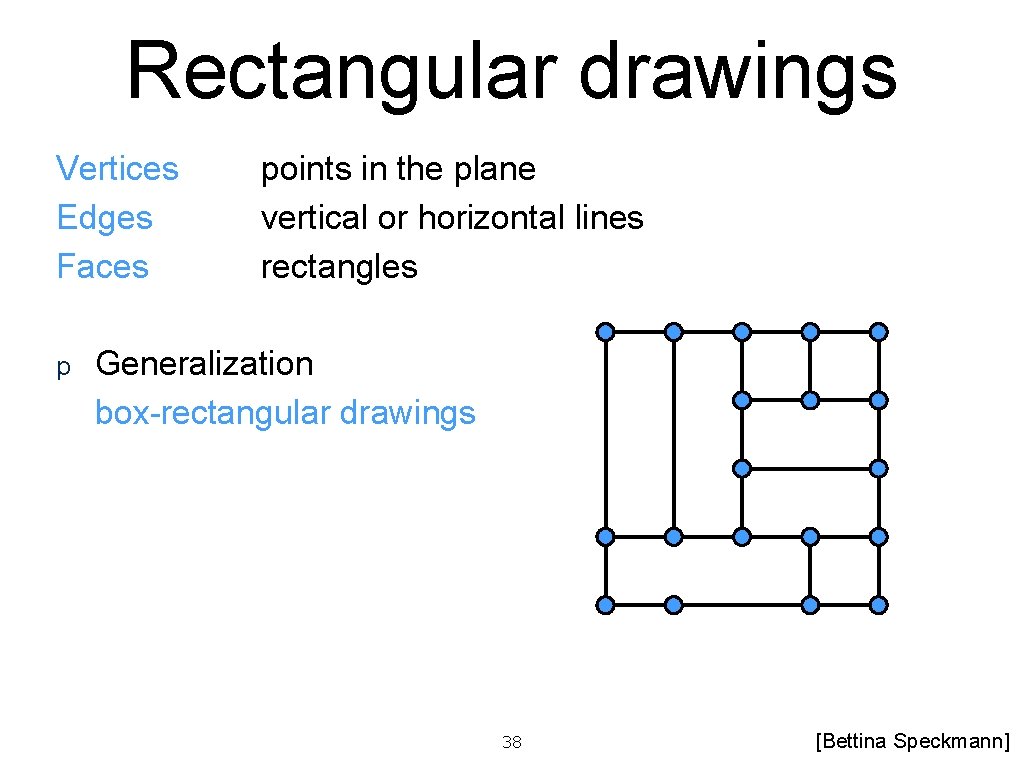
Rectangular drawings Vertices Edges Faces p points in the plane vertical or horizontal lines rectangles Generalization box-rectangular drawings 38 [Bettina Speckmann]

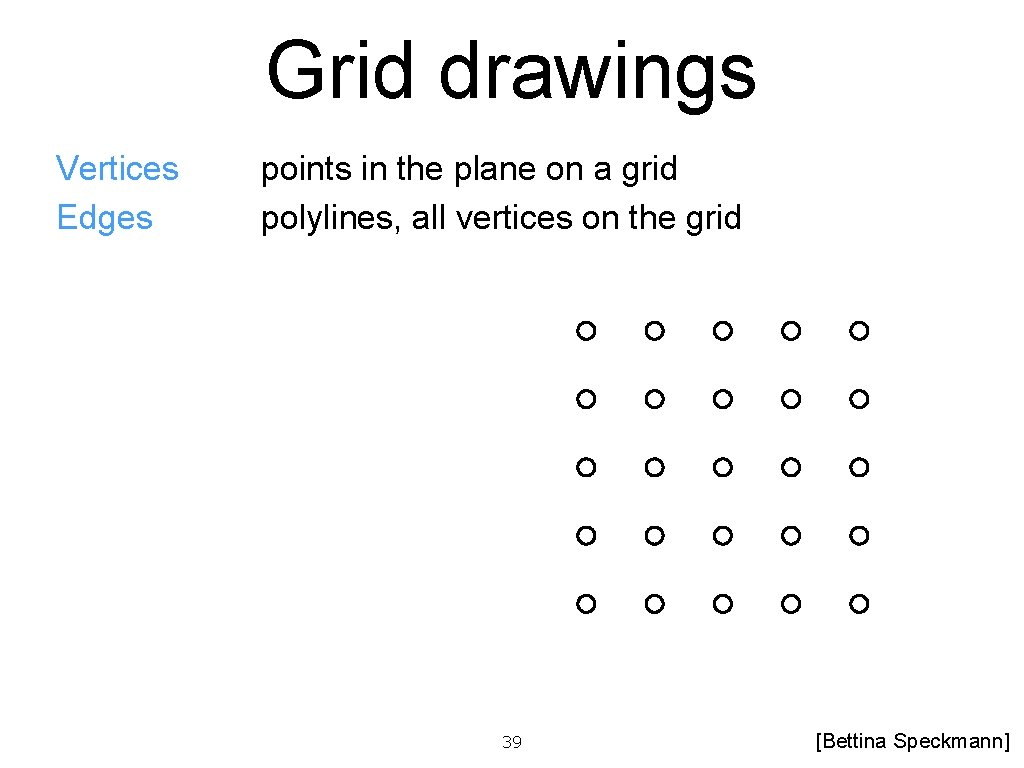
Grid drawings Vertices Edges points in the plane on a grid polylines, all vertices on the grid 39 [Bettina Speckmann]

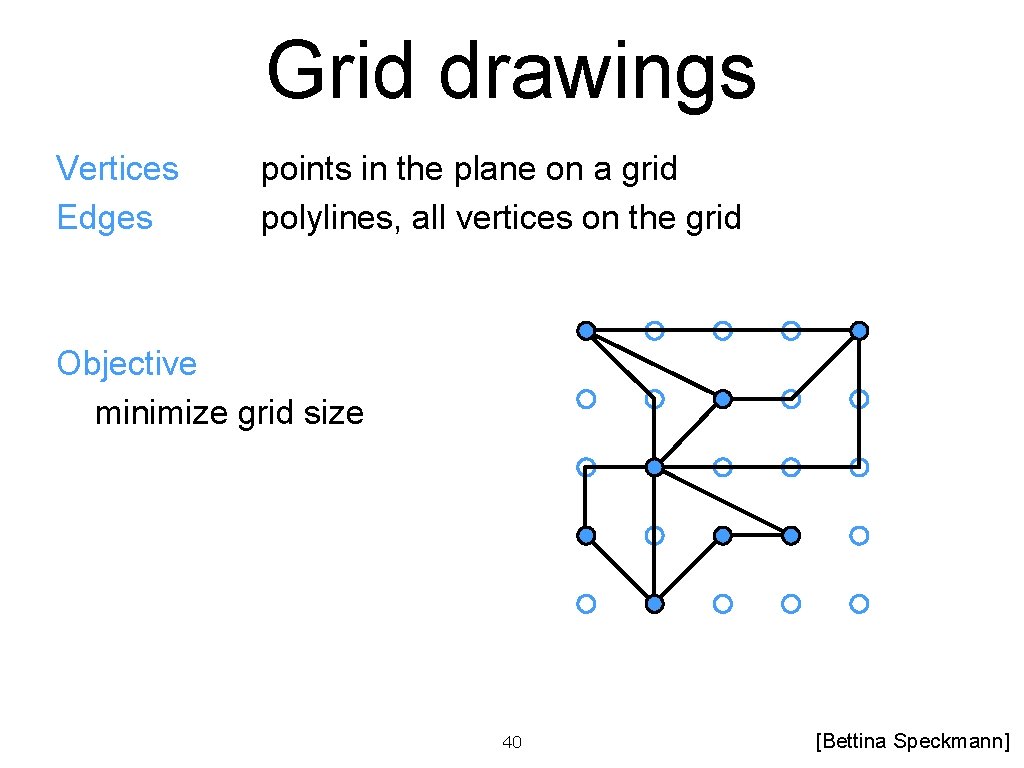
Grid drawings Vertices Edges points in the plane on a grid polylines, all vertices on the grid Objective minimize grid size 40 [Bettina Speckmann]

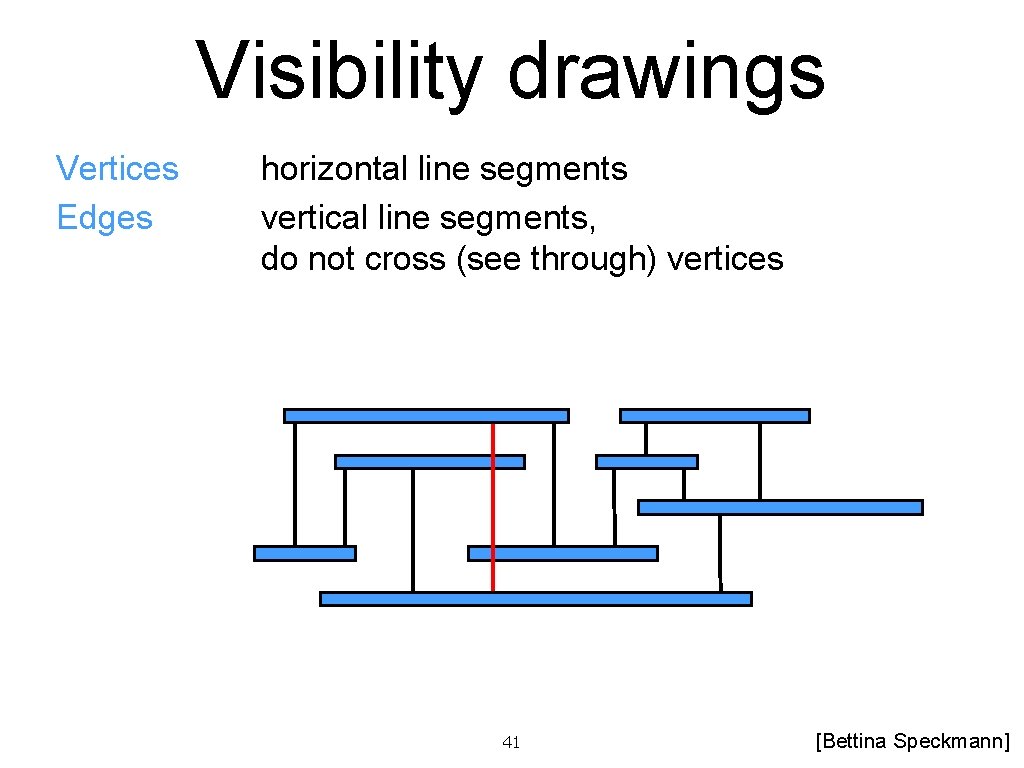
Visibility drawings Vertices Edges horizontal line segments vertical line segments, do not cross (see through) vertices 41 [Bettina Speckmann]

Aesthetics: graphic properties of the drawing that help readability • Minimize number of edge crossings • Minimize number of edge bends • Maximize symmetry • Maximize minimum angle between edges leaving a node • Maximize edge orthogonality • Maximize node orthogonality • Maximize consistent flow direction (digraphs only) Helen C. Purchase Metrics for Graph Drawing Aesthetics Journal of Visual Languages and Computing (2002) 13, 501– 516 42

Aesthetics Further aesthetics criteria [Di Battista Book 99] • Minimize area • Minimize total edge length • Minimize maximal edge length • Minimize variance between edge length • Minimize maximum number of bends on an edge • Minimize aspect ratio, i. e. , ratio of longest side to shortest side of drawing 43

Mental Map • Mental map (cognitive map, mental model): mental representation of a graph, formed by a user by looking at the layout of a graph Misue et al. provide three mathematical models: 1. Orthogonal ordering (horizontal/vertical order) 2. Proximity relation (e. g. , nearest neighbor graph, Delauny triangulation) 3. Topology (expressed by dual graph) K. Misue, P. Eades, W. Lai, K. Sugiyama Layout Adjustment and the Mental Map Journal of Visual Languages and Computing (1995) 6, 183– 210 44

Secondary Notation • Secondary notation: Layout cues that are not formally part of notation but help understanding (e. g. , proximity, symmetry) [Petre CACM’ 95] Marian Petre Why Looking Isn’t Always Seeing: Readership Skills and Graphical Programming Communications of the ACM, June 1995, Vol. 38, No. 6, 33– 44 45

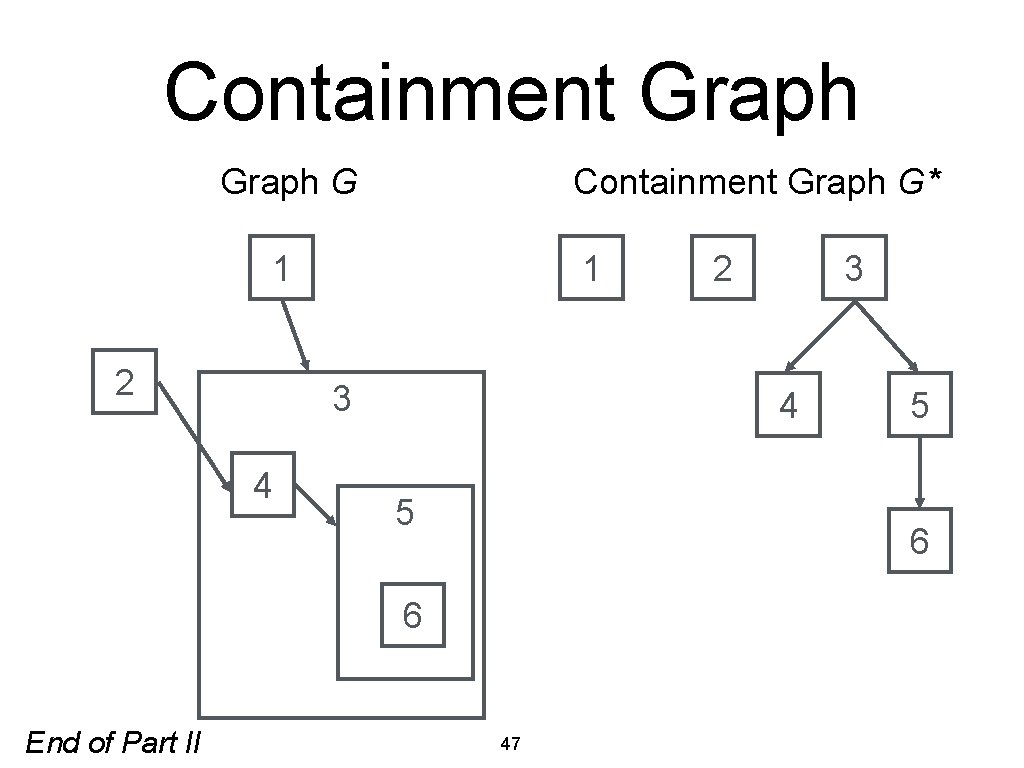
Hierarchical Graph G = (V, E, h) is a hierarchical graph. • h maps each node to its parent, if any: h: V → V ∪ { ⊥ } • For v ∈ V, h -1(v) denotes the node’s children. • h induces a containment graph G* = (V, E*): E* = { (u, v): u, v ∈ V ⋀ u = h(v) } • For h to be valid, we require the containment graph to be acyclic. 46

Containment Graph G* 1 2 1 3 4 5 5 6 6 End of Part II 2 47

Geodesics • Length of a path: number of edges in path • (Graph) geodesic for vertices u, v : a shortest path between u and v • (Graph theoretic) distance between u and v : length of a geodesic for u, v; if there is no geodesic, define distance as infinite 48

Eccentricities • Eccentricity of vertex v : greatest graph theoretic distance between v and any other vertex • Radius r of G : minimum eccentricity of any vertex in G • Diameter d of G : maximum eccentricity of any vertex in G • Central vertex of G : vertex with eccentricity = r • Peripheral vertex of G : vertex with eccentricity = d • Bull graph: • Radius = 2 • Diameter = 3 3 49 2 [Wikimedia commons] 2 2 3

Transitivity • An edge (u, v) of digraph is transitive: there exists a directed path from u to v that does not contain edge (u, v) • Transitive closure G’ of digraph G has an edge (u, v) for every path from u to v • Reduced digraph (transitive reduction): digraph without transitive edges 50

Minors • Contraction of an edge e in G: remove e from G and merge its two incident vertices, u and v, into a new vertex w, where the edges incident to w each correspond to an edge incident to either u or v • A graph H is a minor of a graph G: H can be obtained from G by a series of 0 or more deletions of vertices, deletions of edges, and contraction of edges. 51

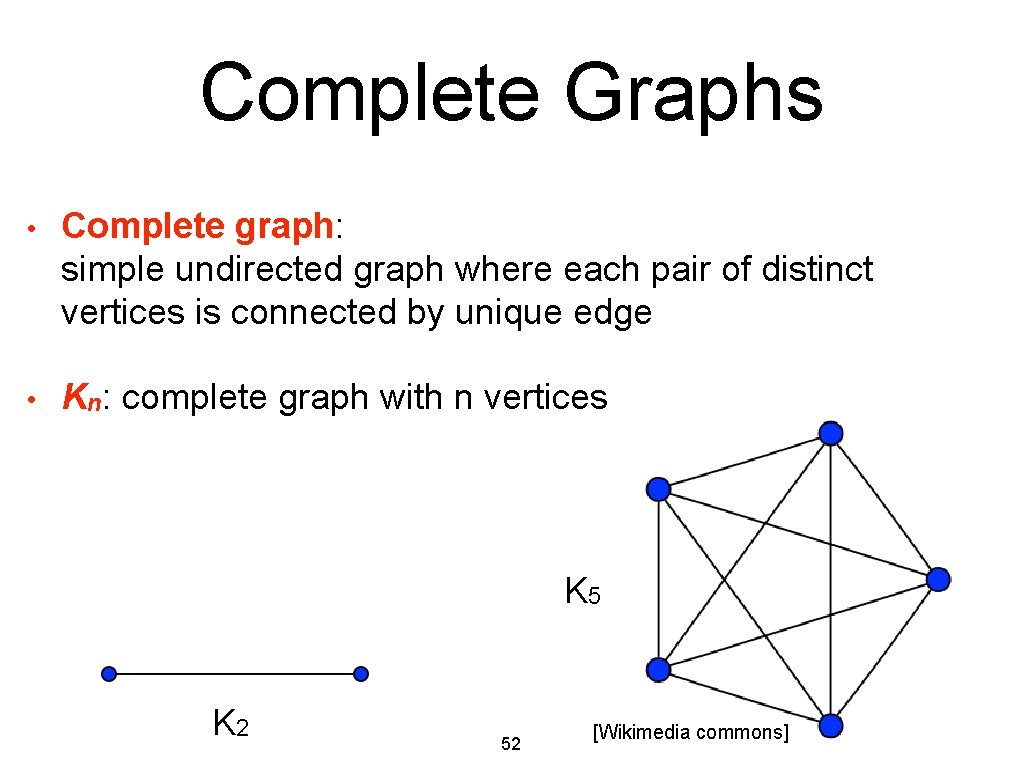
Complete Graphs • Complete graph: simple undirected graph where each pair of distinct vertices is connected by unique edge • Kn: complete graph with n vertices K 5 K 2 52 [Wikimedia commons]

Cliques • Clique: subset of vertices of graph such that its induced subset is complete • All complete graphs are their own maximal cliques • Clique problem: given graph G and integer n, decide whether G has a clique size at least n • Thm: Clique problem is NP-complete 53

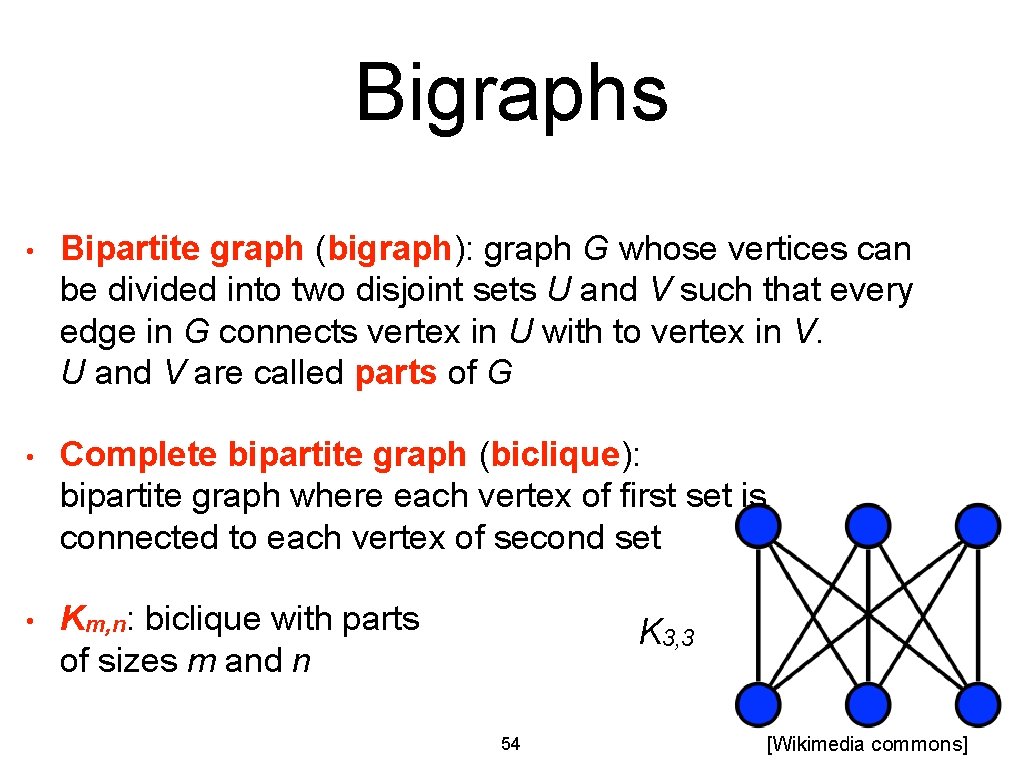
Bigraphs • Bipartite graph (bigraph): graph G whose vertices can be divided into two disjoint sets U and V such that every edge in G connects vertex in U with to vertex in V. U and V are called parts of G • Complete bipartite graph (biclique): bipartite graph where each vertex of first set is connected to each vertex of second set • Km, n: biclique with parts of sizes m and n K 3, 3 54 [Wikimedia commons]

Trees • Forest: acyclic undirected graph. This includes graphs without edges, including the empty graph • Tree: connected forest • Rooted tree: tree in which one vertex has been designated the root • Note: some authors really mean rooted tree when they refer to a tree • Edges of a rooted tree can be assigned a natural orientation, either away from or towards the root, in which case the structure becomes a directed rooted tree 55

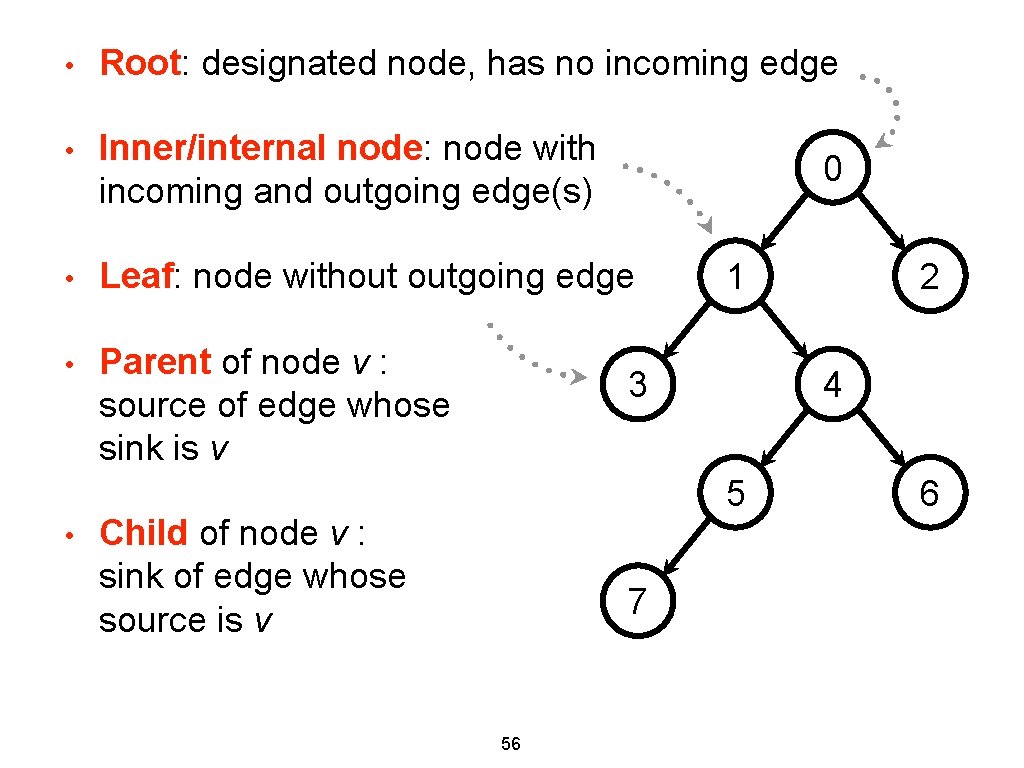
• Root: designated node, has no incoming edge • Inner/internal node: node with incoming and outgoing edge(s) • Leaf: node without outgoing edge • Parent of node v : source of edge whose sink is v • 0 1 3 4 5 Child of node v : sink of edge whose source is v 7 56 2 6

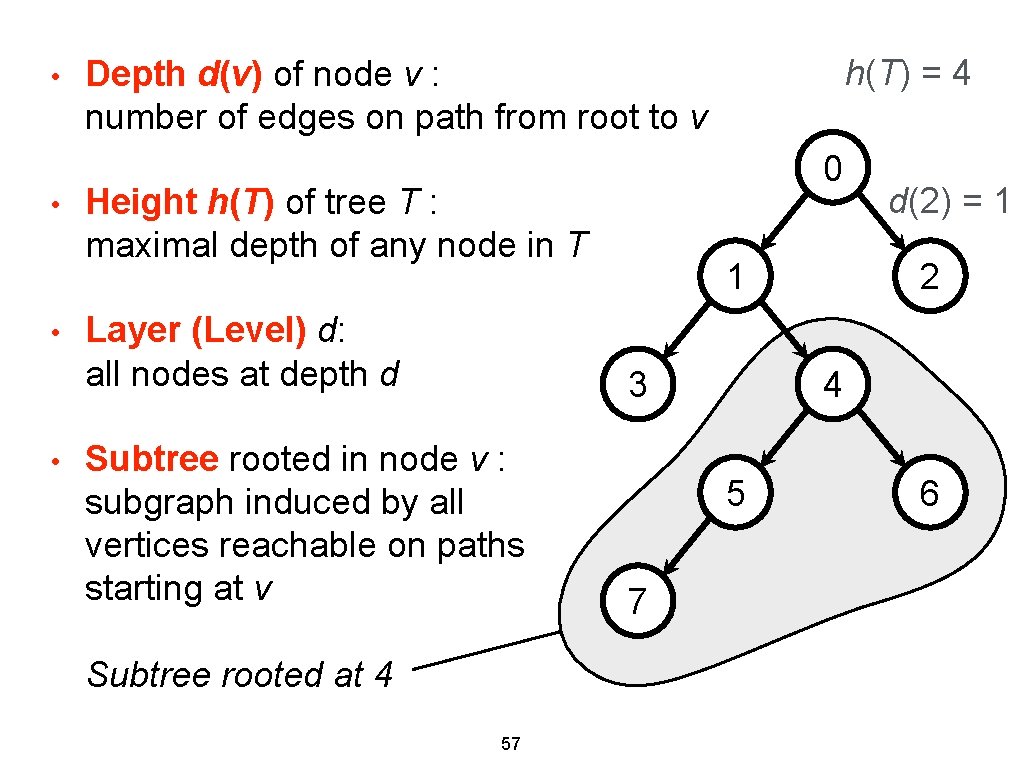
• • h(T) = 4 Depth d(v) of node v : number of edges on path from root to v 0 Height h(T) of tree T : maximal depth of any node in T Layer (Level) d: all nodes at depth d 1 3 Subtree rooted in node v : subgraph induced by all vertices reachable on paths starting at v Subtree rooted at 4 57 2 4 5 7 d(2) = 1 6

Binary Trees • Ordered tree: rooted tree, with ordering for children of v for each node v • Binary tree: rooted tree, each vertex has at most two children • Typically assume that binary trees are ordered • Child order determines left child and right child. Note: may have only left or only right child • Left/right subtree of node v: subtree rooted in left/right child of v. If there is no left/right child, the left/right subtrees are empty. • Left/right contour of tree T of height h: sequence of vertices v 0, … vh s. t. vi, is leftmost/rightmost vertex of T at layer i 58 0 1 3 4 5 7 2 6

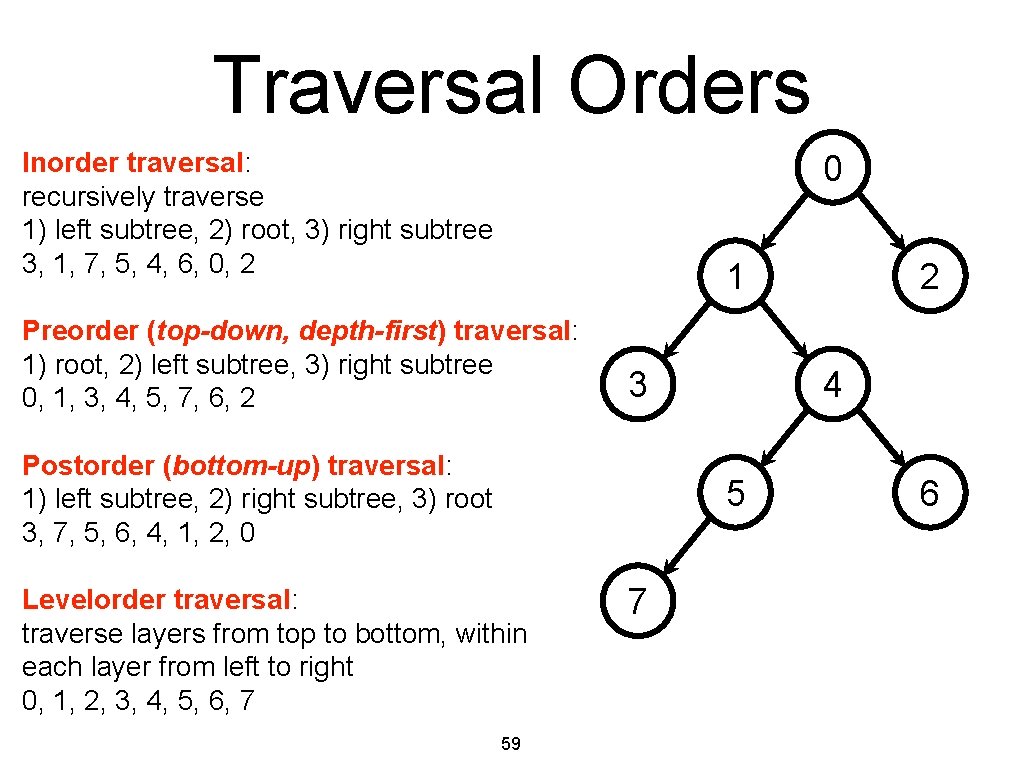
Traversal Orders Inorder traversal: recursively traverse 1) left subtree, 2) root, 3) right subtree 3, 1, 7, 5, 4, 6, 0, 2 0 1 Preorder (top-down, depth-first) traversal: 1) root, 2) left subtree, 3) right subtree 0, 1, 3, 4, 5, 7, 6, 2 3 Postorder (bottom-up) traversal: 1) left subtree, 2) right subtree, 3) root 3, 7, 5, 6, 4, 1, 2, 0 4 5 Levelorder traversal: traverse layers from top to bottom, within each layer from left to right 0, 1, 2, 3, 4, 5, 6, 7 59 7 2 6

Isomorphisms Consider binary trees T 1, T 2 are simply isomorphic if they meet either of the following conditions: 1. T 1 and T 2 are both empty 2. T 1 and T 2 are both non-empty, the left subtrees of T 1 and T 2 are simply isomorphic and the right subtrees of T 1 and T 2 are simply isomorphic T 1, T 2 are axially isomorphic if T 1 is simply isomorphic to the binary tree obtained from T 2 by exchanging the left and right subtrees of each vertex End of Part III 60