InfGraph Draw Automatic Graph Drawing Lecture 13 Topology

Inf-Graph. Draw: Automatic Graph Drawing Lecture 13 Topology – Shape – Metrics Reinhard von Hanxleden rvh@informatik. uni-kiel. de Most definitions are from [Di Battista Book 99]. This lecture is based in part on material kindly provided by Peter Eades, Bettina Speckmann and Kees Wisser 1

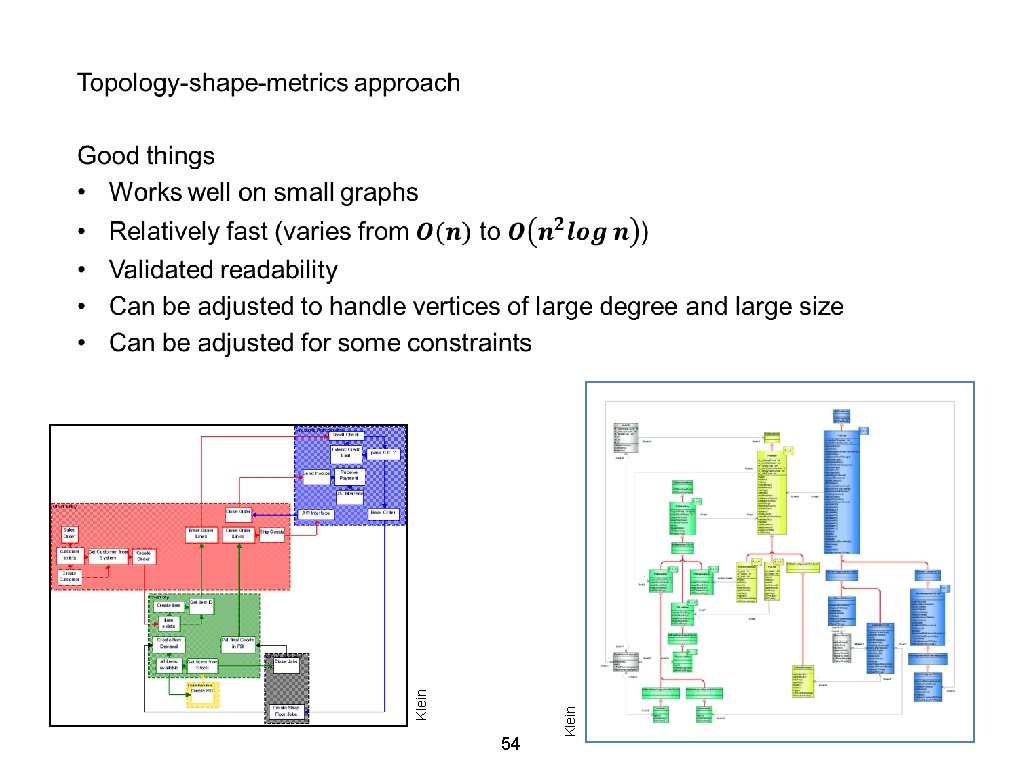
5 -Minute Review 1. How can we test for planarity? What runtime does that approach have? 2. What is an optimal weighted topological numbering? 3. What is an ST graph? 4. What is a tesselation representation, how can we construct it for an ST graph? 5. How does the Topology-Shape-Metrics approach work?

Topology – Shape – Metrics [Paul Klose] Input: a graph G Algorithm: 1. Topology: Compute a good topological embedding of G 2. Shape: Compute a good orthogonal shape for this topological embedding 3. Metrics: Compute a good orthogonal grid drawing of G Output: an orthogonal grid drawing of G 3

Topology – Shape – Metrics [Paul Klose] Input: a graph G Algorithm: 1. Topology: Compute a good topological embedding of G 2. Shape: Compute a good orthogonal shape for this topological embedding 3. Metrics: Compute a good orthogonal grid drawing of G Output: an orthogonal grid drawing of G 4

Shape: Orthogonal Drawing References: [Tamassia 87] R. Tamassia, On embedding a graph in the grid with the minimum number of bends, SIAM Journal on Computing, 16(3), 1987, 421– 444 [Di Battista et al. 99], Sec. 5. 3 The following slides are based on material from Kees Visser 5

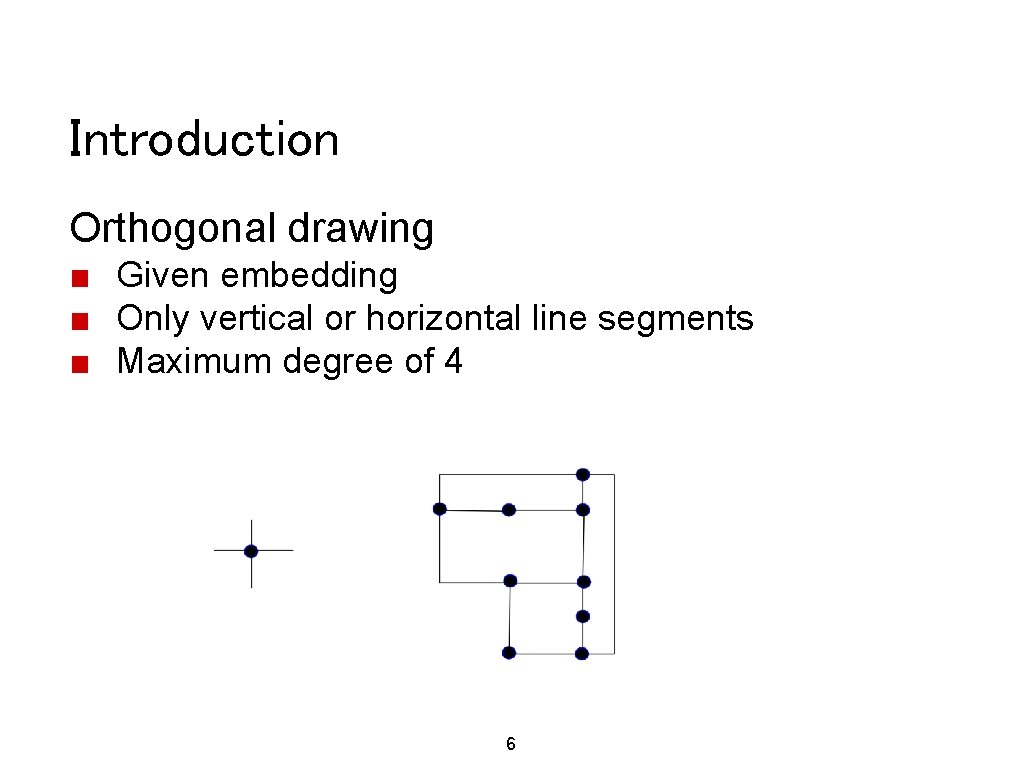
Introduction Orthogonal drawing ■ Given embedding ■ Only vertical or horizontal line segments ■ Maximum degree of 4 6

Introduction □ Used in VLSI circuits □ Minimize bends □ Finding an orthogonal drawing of graph G with the minimum number of bends without a fixed embedding is NP-Complete 7

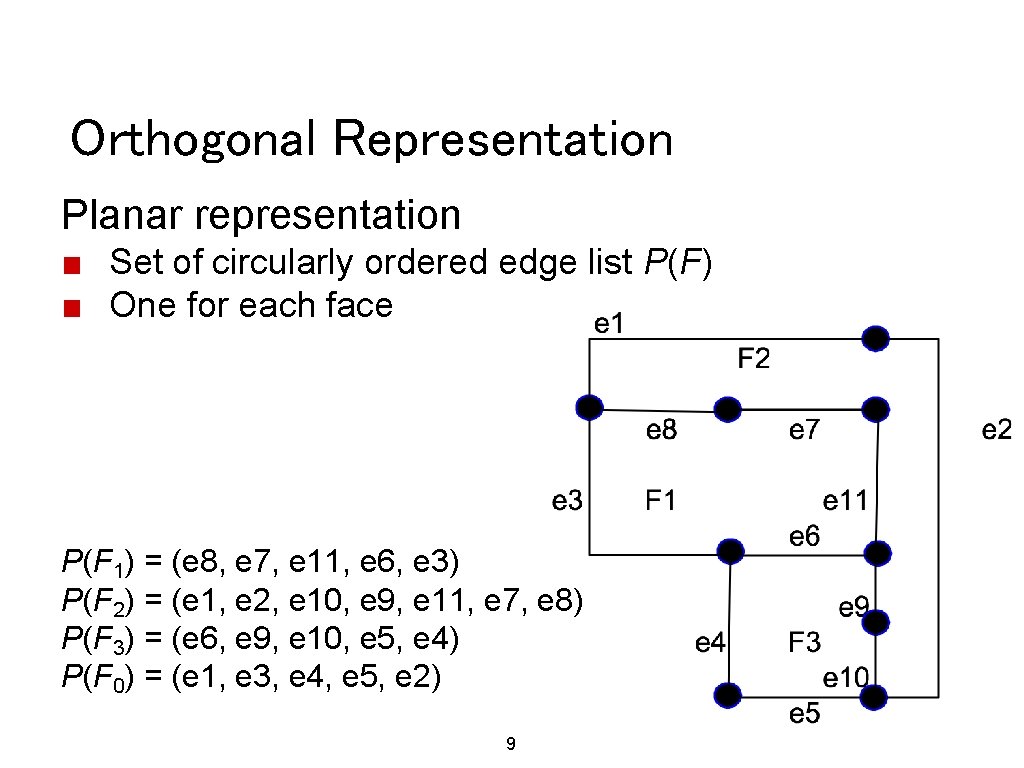
Orthogonal Representation Planar representation ■ Set of circularly ordered edge list P(F) ■ One for each face P(F 1) = (e 8, e 7, e 11, e 6, e 3) P(F 2) = (e 1, e 2, e 10, e 9, e 11, e 7, e 8) P(F 3) = (e 6, e 9, e 10, e 5, e 4) P(F 0) = (e 1, e 3, e 4, e 5, e 2) 9

Orthogonal Representation Definitions: ■ Bridge: edge that appears twice in same list ■ Vertex angle: angle formed by to edges ■ Bend angle: angle formed by two line segments at a bend Both vertex angles and bend angles are 90, 180, 270 or 360 degrees 10

Orthogonal representation Facts: ■ Sum of vertex angles around any vertex is 360 degrees ■ For p: number of polygon edges, sum of angles inside inner facial polygon is (2 p – 4) ∙ 90 degrees, and sum of angles of outer facial polygon is (2 p + 4) ∙ 90 degrees 11

Orthogonal representation One list R(F) for each face F Each element r in the list has 3 values: ■ Er: edge ■ Sr: bit string, indicating bends in line 0: 90 degree bend 1: 270 degrees ε: straight line ■ Ar: angle formed in the face from this edge to next edge 12

R(F 1) = ((e 8, ε, 180), (e 7, ε, 90), (e 11, ε, 90), (e 6, ε, 180), (e 3, 0, 90)) R(F 2) = ((e 1, 0, 180), (e 2, 00, 90), (e 10, ε, 180), (e 9, ε, 180), (e 11, ε, 270), (e 7, ε, 180), (e 8, ε, 90)) 13

Necessary properties of orthogonal representation: (p 1) There is some planar graph whose planar representation is given by the E-fields of the list in R. (p 2) For each pair of elements r and r’ in R with Er = Er’, can obtain Sr’ by applying bitwise negation to the reversion of Sr. (p 3) For each element r in R, define the rotation p(r) as follows: p(r) = |Sr|0 – |Sr|1 + 2 – Ar/90, where |Sr|0/1 denote the number of 0’s/1’s in Sr. Then Σr∈R(F) p(r) = -4 if F is external face, +4 otherwise. (p 4) For each vertex v, the sum of the vertex angles around v given by the A-fields in R is equal to 360 degrees. 14

Flow network – Sources, Sinks A flow network N is a directed graph with two disjoint non-empty sets of sources and sinks σ(u): production of source u -σ(u): consumption of sink u 15

Flow network – Arcs, Flow Each arc e of N is labelled with 3 nonnegative integers λ(e): lower bound μ(e): capacity c(e): cost Flow Ф(e) Must have λ(e) ≤ Ф(e) ≤ μ(e) Also for all sources/sinks u and their adjacent nodes v, must have σ(u) = Σv Ф(u, v) – Σv Ф(v, u) 16

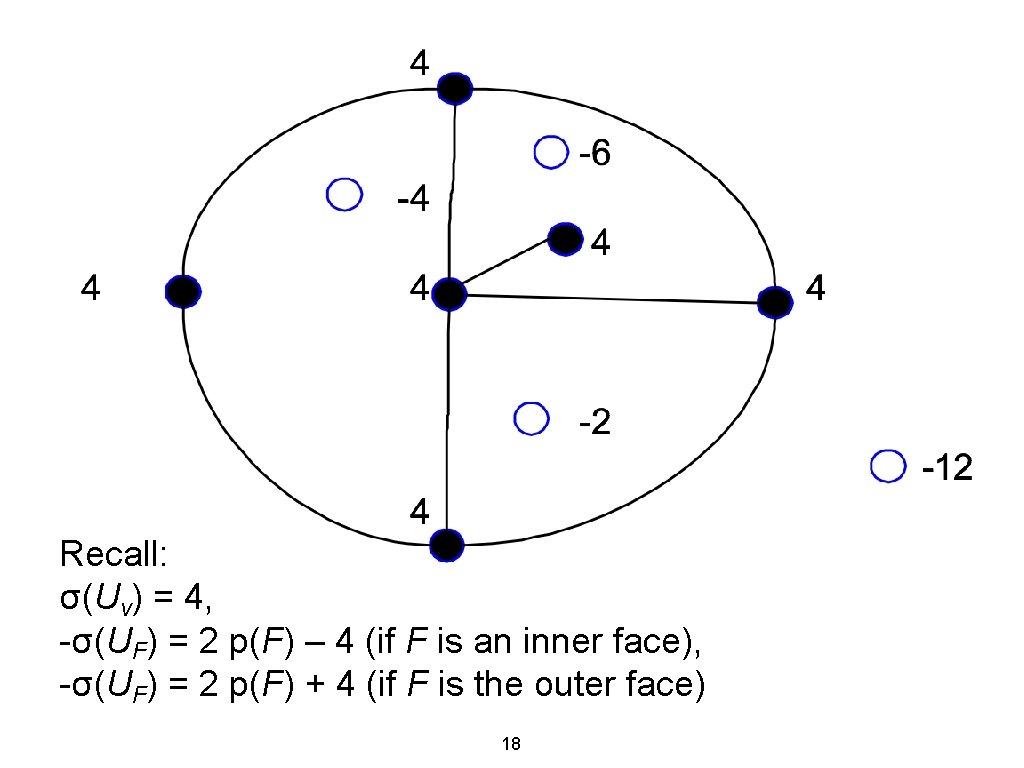
Bend-optimal drawing One unit of flow represents angle of 90 degrees Each vertex and face is a node Each vertex node Uv is a source, σ(Uv) = 4 Each face node UF is a sink, -σ(UF) = 2 p(F) – 4 (if F is an inner face), -σ(UF) = 2 p(F) + 4 (if F is the outer face), where p(F) is number of vertex angles in F 17

Recall: σ(Uv) = 4, -σ(UF) = 2 p(F) – 4 (if F is an inner face), -σ(UF) = 2 p(F) + 4 (if F is the outer face) 18

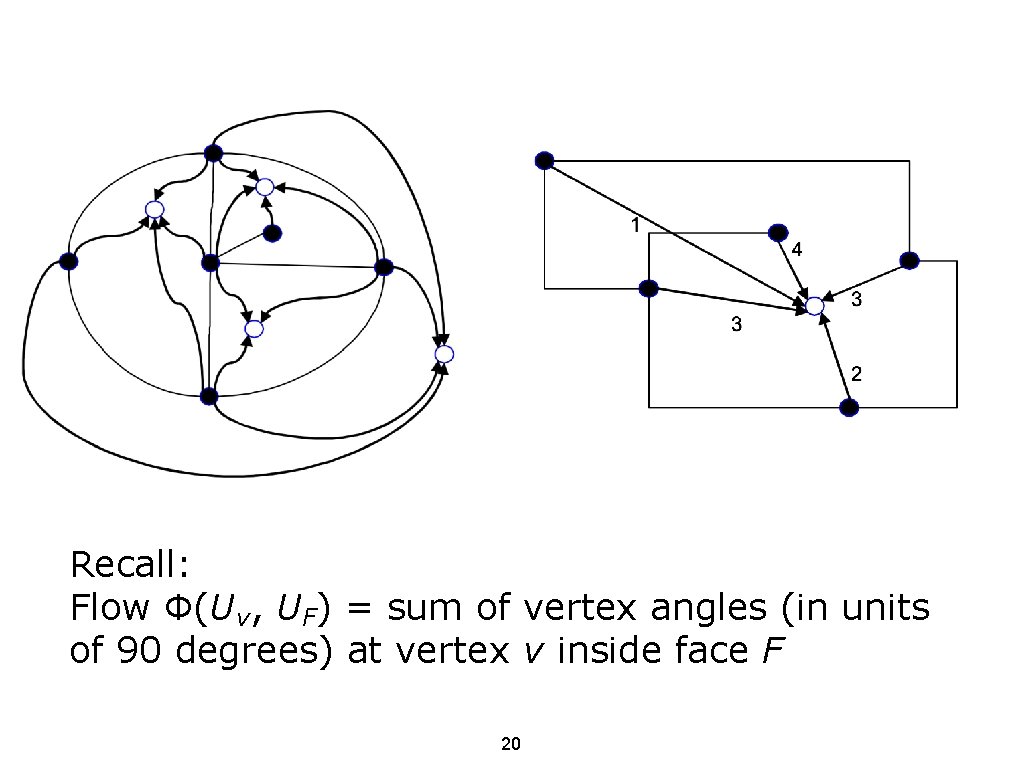
Bend-optimal drawing Arc set of network N: vertex arcs (Av) + face arcs (AF) Av: arcs from every vertex node to every face node that the vertex borders Flow Ф(Uv, UF) = sum of vertex angles (in units of 90 degrees) at vertex v inside face F λ(Uv, UF) = number of vertex angles at v inside F μ(Uv, UF) = 4 c(Uv, UF) = 0 19

Recall: Flow Ф(Uv, UF) = sum of vertex angles (in units of 90 degrees) at vertex v inside face F 20

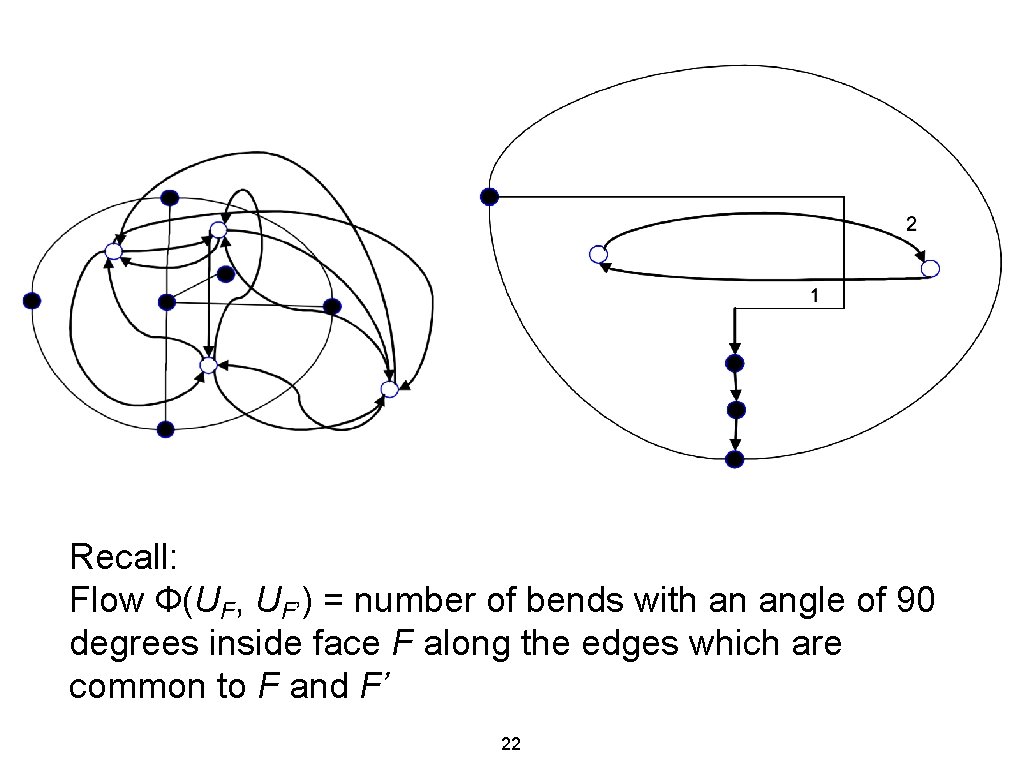
Bend-optimal drawing AF: arcs from every face F to face F’ that shares an edge with F Note: bridge in G induces self-loop in AF Flow Ф(UF, UF’) = number of bends with an angle of 90 degrees inside face F along the edges which are common to F and F’ λ(UF, UF’) = 0 μ(UF, UF’) = +∞ c(UF, UF) = 1 21

Recall: Flow Ф(UF, UF’) = number of bends with an angle of 90 degrees inside face F along the edges which are common to F and F’ 22

Theorem: Let G be a plane graph, let N be the network constructed from G. For each integer flow Ф in network N, there is an orthogonal representation R that represents an orthogonal drawing D of G and whose number of bends is equal to the cost of the flow Ф. In particular, the minimum cost flow can be used to construct a bend-optimal orthogonal drawing of G. 23

Proof We construct an orthogonal representation R of G by computing the A- and S-fields from the flow values in Av and AF, respectively. Compute A-fields: For (v, F) ∈ Av, define R(v, F) = {r ∈ R(F) : both Er and Er’, where r’ follows r in R(F), are incident to v } (why both? ) R(v, F) = {r 1, r 2, …, r. L}, where 1 ≤ L ≤ 4 (why? ) L denotes how often v occurs in contour of F. Ar 1 = 90(Ф(Uv, UF) – L + 1) Ari = 90 for each i, 2 ≤ i ≤ L 24

Compute S-fields: For each arc (F, F’) in AF, define R(F, F’) = {r ∈ R(F) : Er is between F and F’ } For each pair of arcs (F, F’), (F’, F) in AF, let r 1, … , r. L be the elements of R(F, F’), and r’ 1, … , r’L be corresponding elements R(F’, F), i. e. , Eri = Er’i Note: if F = F’, then ri , r’i are pairs of elements corresponding to two sides of same bridge Set Sri = Sr’i = ε for each i: 2 ≤ i ≤ L If F = F’, set Sr 1 = 0^Ф(UF , UF’) and Sr’ 1 = 1^Ф(UF , UF’) O. w. , Sr 1 = 0^Ф(UF , UF’) 1^Ф(UF’ , UF) and Sr’ 1 = 0^Ф(UF’ , UF) 1^Ф(UF , UF’) where 0/1^a denotes a string of a 0’s/1’s e 1 Example: Er 1 = Er’ 1 = e 1, Er 2 = Er’ 2 = e 2, Er 3 = Er’ 3 = e 3 L = 3, Ф(UF , UF’) = 2 and Ф(UF’ , UF) = 1 Sr 1 = 001 , Sr’ 1 = 011 and Sr 2 = Sr’ 2 = Sr 3 = Sr’ 3 = ε 25 F e 2 e 3 F‘

Recall: necessary properties for R(F) (p 1) There is some planar graph whose planar representation is given by the E-fields of the list in R. This is automatically satisfied since we have built R from a planar representation (p 2) For each pair of elements r and r’ in R with Er = Er’, can obtain Sr’ by applying bitwise negation to the reversion of Sr. This follows from the assignment of the S-values. 26

Recall: necessary properties for R(F) (p 3) For each element r in R, define the rotation p(r) as follows: p(r) = |Sr|0 – |Sr|1 + 2 – Ar/90, where |Sr|0/1 denote the number of 0’s/1’s in Sr. Then Σr∈R(F) p(r) = -4 if F is external face, +4 otherwise. This follows from the definition that every source produces 4 units. (p 4) For each vertex v, the sum of the vertex angles around v given by the A-fields in R is equal to 360 degrees. Solving the equation by replacing with the flow equations makes this satisfied (exercise). 27

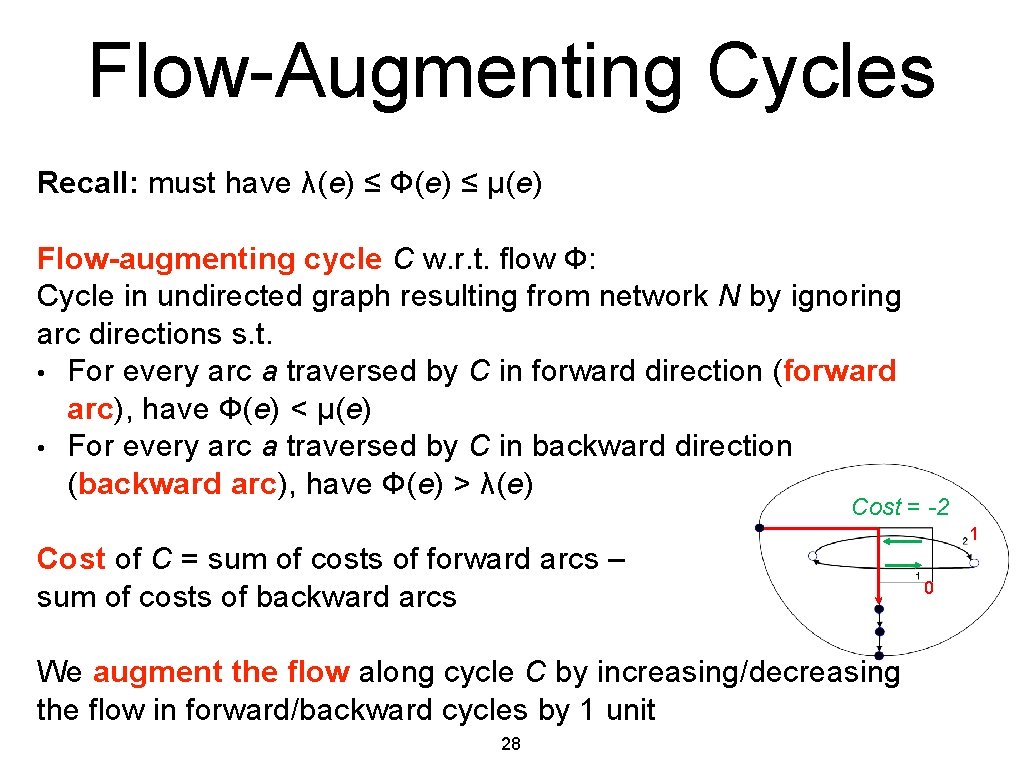
Flow-Augmenting Cycles Recall: must have λ(e) ≤ Ф(e) ≤ μ(e) Flow-augmenting cycle C w. r. t. flow Ф: Cycle in undirected graph resulting from network N by ignoring arc directions s. t. • For every arc a traversed by C in forward direction (forward arc), have Ф(e) < μ(e) • For every arc a traversed by C in backward direction (backward arc), have Ф(e) > λ(e) Cost = -2 Cost of C = sum of costs of forward arcs – sum of costs of backward arcs We augment the flow along cycle C by increasing/decreasing the flow in forward/backward cycles by 1 unit 28 1 0

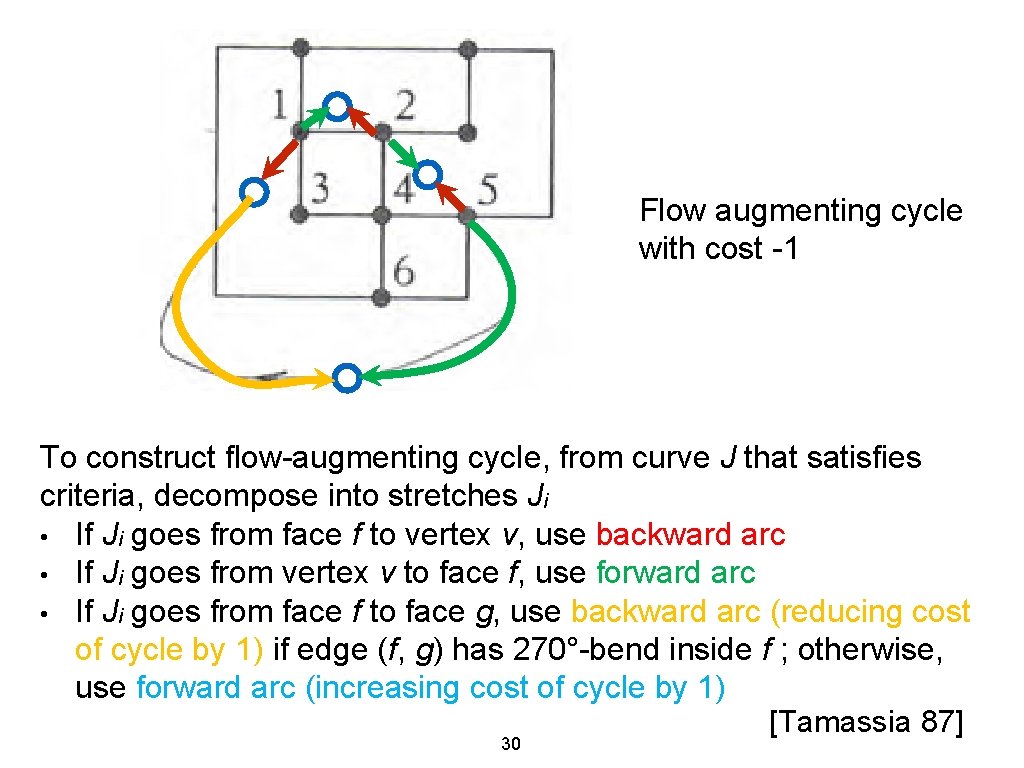
Minimizing Bends Theorem: Flow Ф of network N is of minimum cost iff N has no flowaugmenting cycles of negative costs. Applied to our problem: Theorem: Orthogonal graph G has minimum number of bends among all orthogonal graphs with same planar representation iff there is no directed closed simple curve J s. t. 1. J intersects each edge of G at most twice 2. J enters vertices of G only from angles ≥ 180° 3. More than half of the edges crossed by J have a bend with angle 270° from the side from which J enters If there is such a J: • At vertices, decrease entering angle by 90° • At edges with 270° entering bend(s), eliminate one such bend • At other edges, add 90° entering bend 29

Flow augmenting cycle with cost -1 To construct flow-augmenting cycle, from curve J that satisfies criteria, decompose into stretches Ji • If Ji goes from face f to vertex v, use backward arc • If Ji goes from vertex v to face f, use forward arc • If Ji goes from face f to face g, use backward arc (reducing cost of cycle by 1) if edge (f, g) has 270°-bend inside f ; otherwise, use forward arc (increasing cost of cycle by 1) [Tamassia 87] 30

Minimizing Bends � � 31 [Tamassia 87]

Efficiency Garg and Tamassia [GD‘ 96] have shown that the minimum cost flow problem in this specific network can be solved in time O(n 7/4 log n) 32

Topology – Shape – Metrics [Paul Klose] Input: a graph G Algorithm: 1. Topology: Compute a good topological embedding of G 2. Shape: Compute a good orthogonal shape for this topological embedding 3. Metrics: Compute a good orthogonal grid drawing of G Output: an orthogonal grid drawing of G 33

Compaction of Orthogonal Representations • Want to assign lengths to segments of edges of orthogonal representation • No crossings or overlaps among vertices and edges • Want to minimize area, while using integer lengths • For n vertices and b bends, can construct drawing of O((n + b)2) area, in O(n + b) time • First, consider case where each face has rectangular shape 34

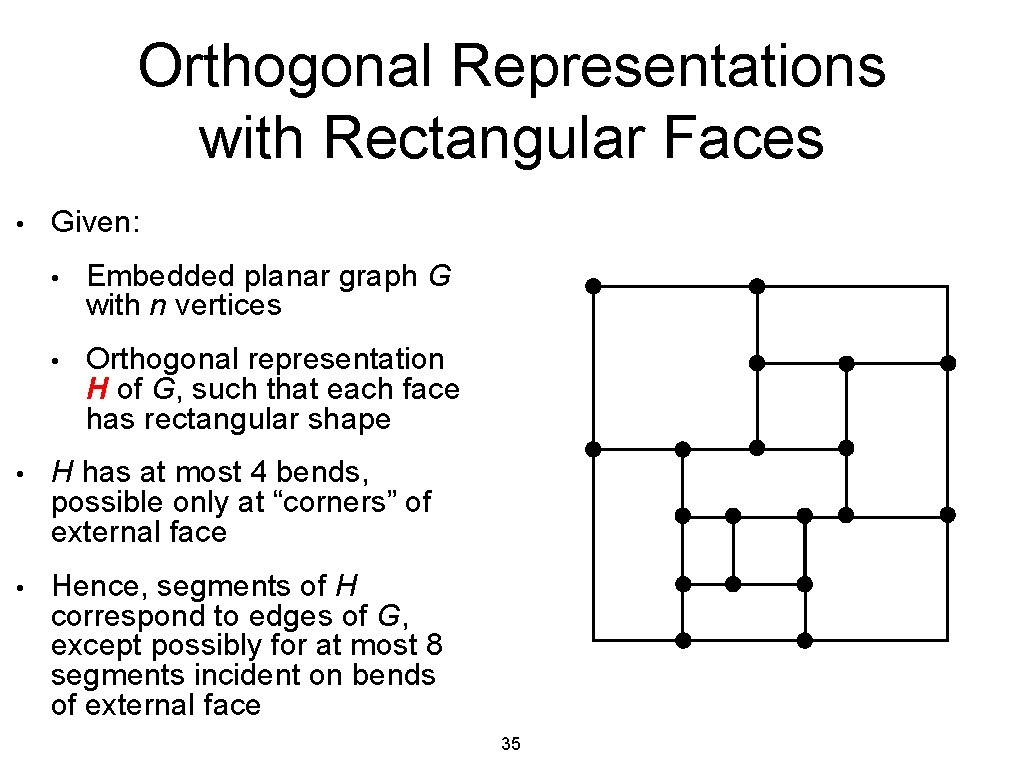
Orthogonal Representations with Rectangular Faces • Given: • Embedded planar graph G with n vertices • Orthogonal representation H of G, such that each face has rectangular shape • H has at most 4 bends, possible only at “corners” of external face • Hence, segments of H correspond to edges of G, except possibly for at most 8 segments incident on bends of external face 35

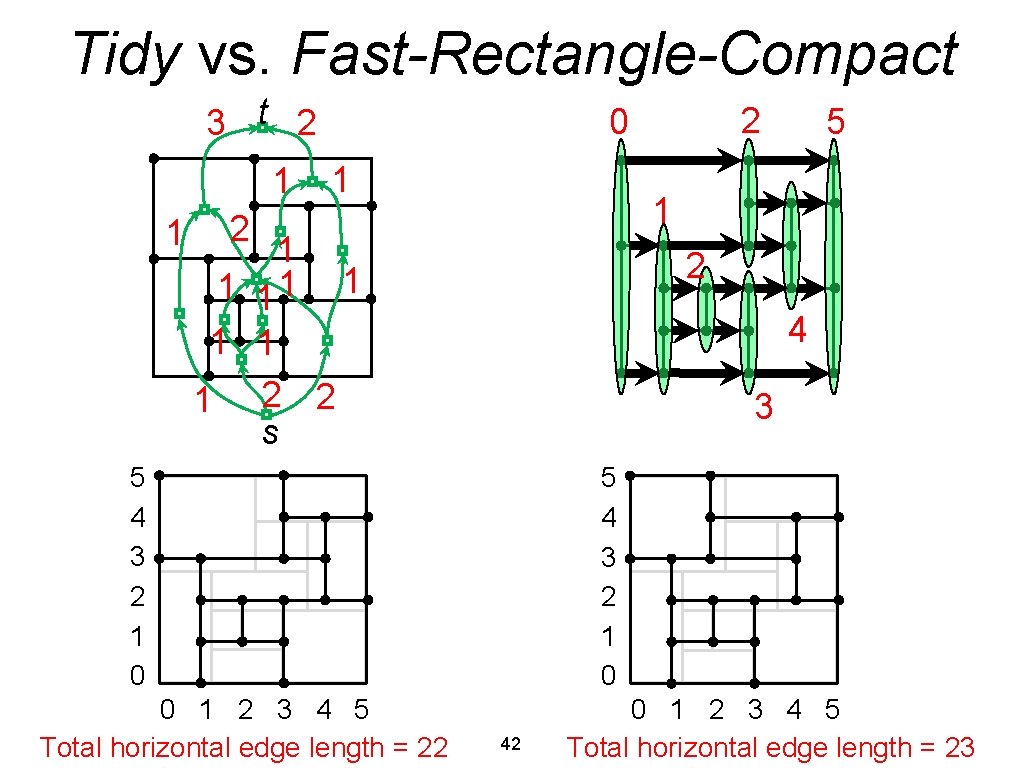
Algorithm 5. 2: Tidy-Rectangle-Compact • Input: embedded planar graph G with n vertices of max. degree 4; orthogonal representation H of G, such that each face has rectangular shape • Output: planar orthogonal grid drawing Γ of G with orthogonal representation H and minimum height, width, area and total edge length 1. Construct flow networks Nhor and Nver associated with H 2. Compute minimum cost flows for Nhor and Nver 3. Set length of each segment of H to flow in corresponding arc of Nhor or Nver 36

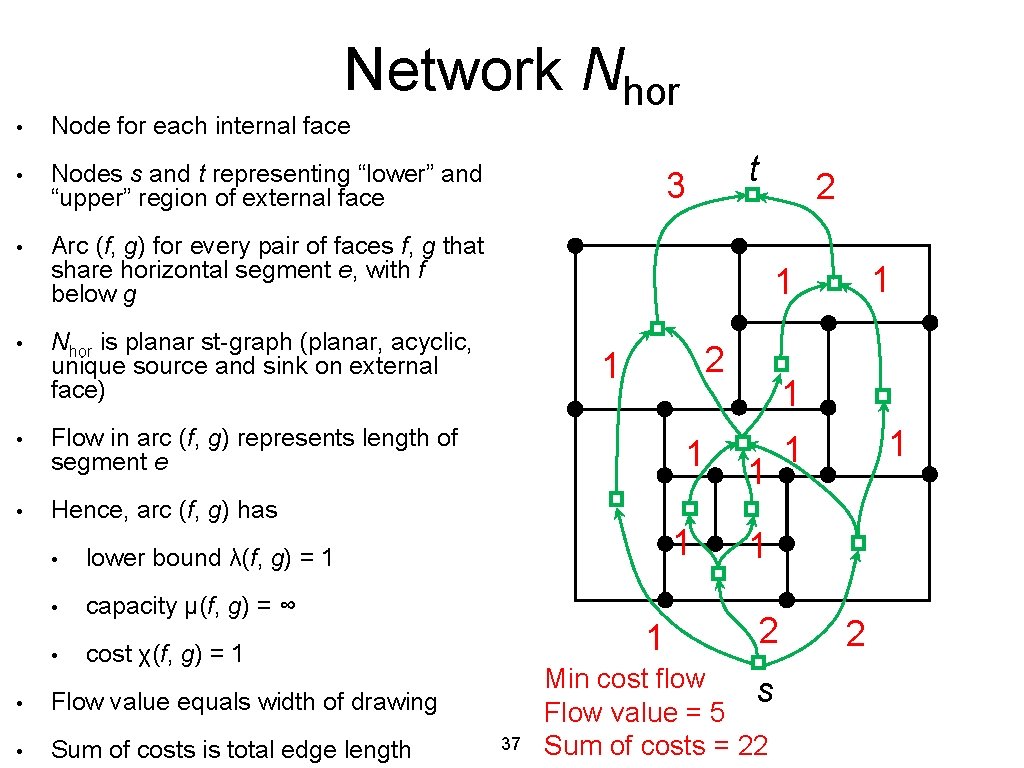
Network Nhor • Node for each internal face • Nodes s and t representing “lower” and “upper” region of external face • Arc (f, g) for every pair of faces f, g that share horizontal segment e, with f below g • • • 3 2 1 Flow in arc (f, g) represents length of segment e 1 Hence, arc (f, g) has lower bound λ(f, g) = 1 • capacity μ(f, g) = ∞ • cost χ(f, g) = 1 • Flow value equals width of drawing • Sum of costs is total edge length 2 1 1 Nhor is planar st-graph (planar, acyclic, unique source and sink on external face) • t 1 1 37 1 1 1 2 Min cost flow s Flow value = 5 Sum of costs = 22 2

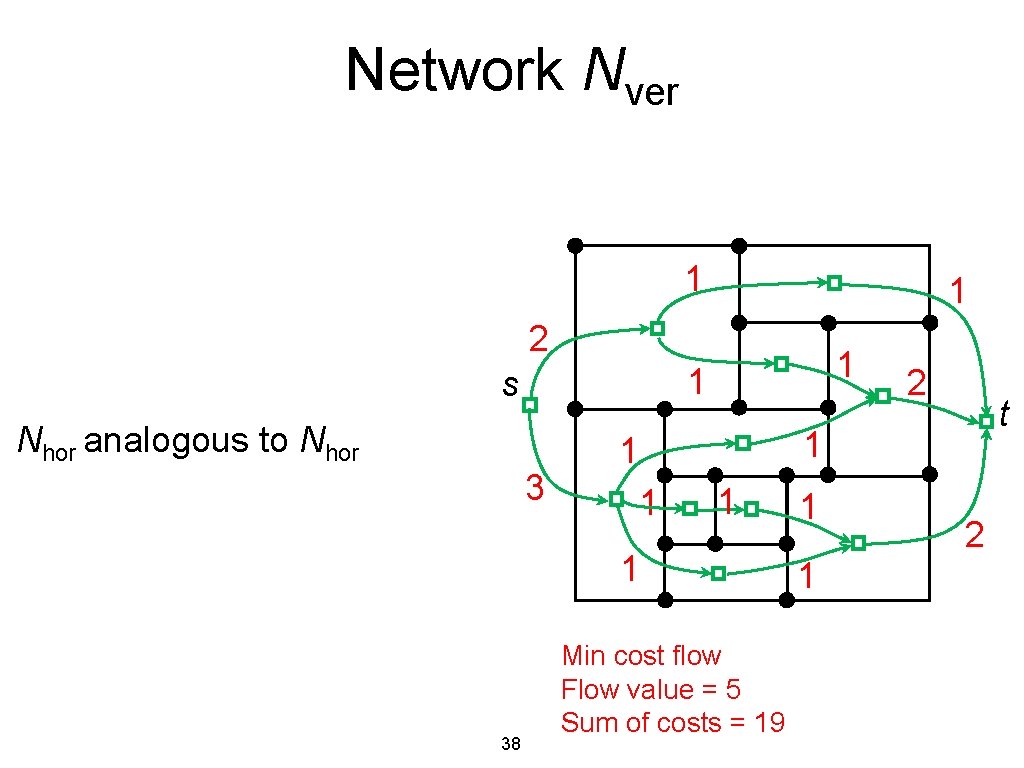
Network Nver 1 1 2 1 1 s Nhor analogous to Nhor 3 1 1 t 1 1 1 38 2 Min cost flow Flow value = 5 Sum of costs = 19 1 1 2

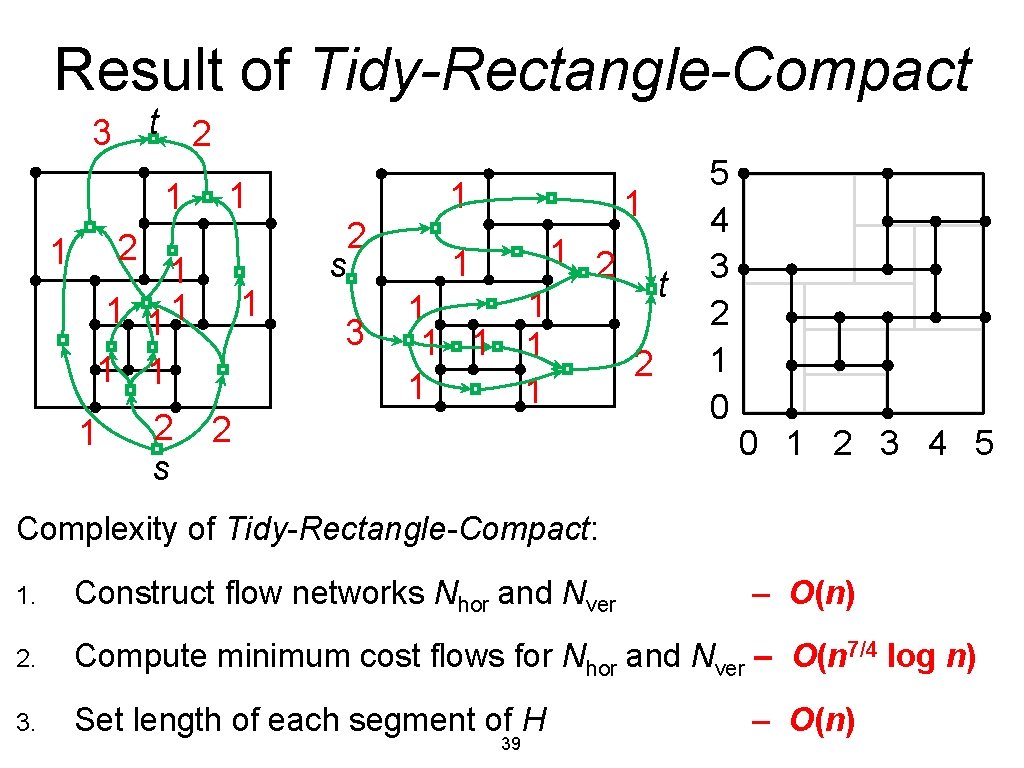
Result of Tidy-Rectangle-Compact t 2 3 1 1 2 1 11 1 1 2 s 2 2 s 3 1 1 1 2 1 1 1 1 t 2 5 4 3 2 1 0 0 1 2 3 4 5 Complexity of Tidy-Rectangle-Compact: 1. Construct flow networks Nhor and Nver 2. Compute minimum cost flows for Nhor and Nver – O(n 7/4 log n) 3. Set length of each segment of H 39 – O(n)

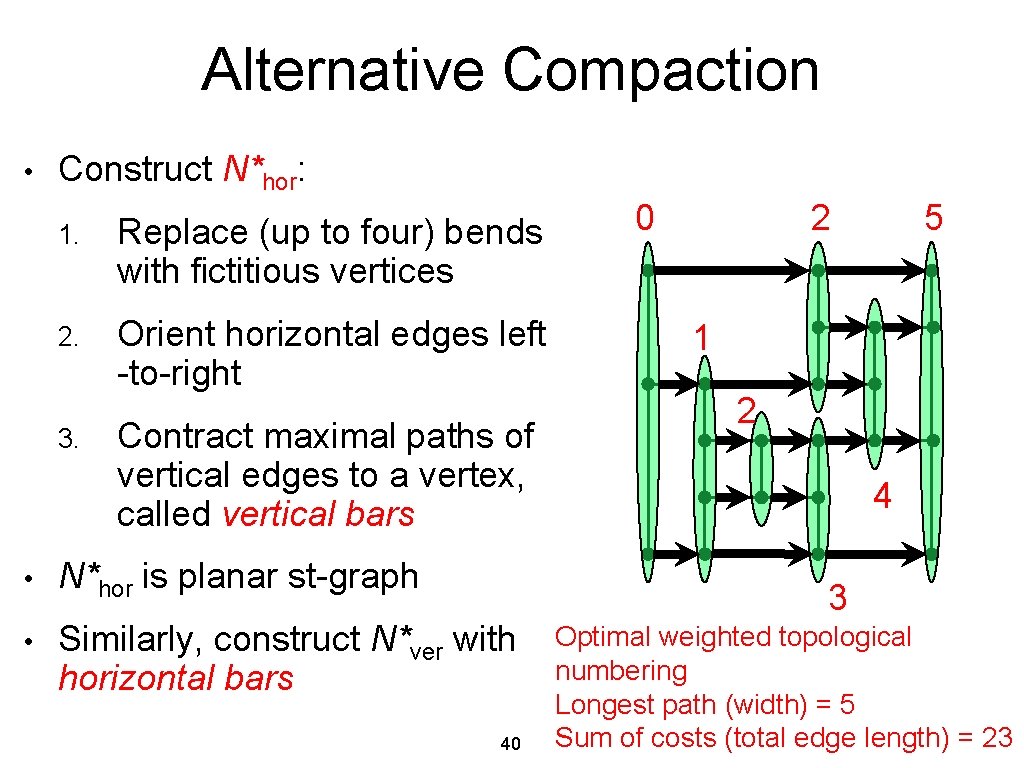
Alternative Compaction • Construct N*hor: 1. Replace (up to four) bends with fictitious vertices 2. Orient horizontal edges left -to-right 3. Contract maximal paths of vertical edges to a vertex, called vertical bars • N*hor is planar st-graph • Similarly, construct N*ver with horizontal bars 2 0 5 1 2 4 3 40 Optimal weighted topological numbering Longest path (width) = 5 Sum of costs (total edge length) = 23

Algorithm 5. 3: Fast-Rectangle-Compact • Input: embedded planar graph G with n vertices of max. degree 4; orthogonal representation H of G, such that each face has rectangular shape • Output: planar orthogonal grid drawing Γ of G with orthogonal representation H and minimum height, width, and area 1. Construct planar st-graphs N*hor and N*ver and assign unit weights to their edges 2. Compute optimal weighted topological numberings X and Y for N*hor and N*ver 3. Set length of each horizontal segment e of H equal to X(b’’) – X(b’), where b’ and b’’ are the vertical bars of N*hor containing the left and right endpoint of segment e, respectively 4. Set length of each vertical segment e of H equal to Y(b’’) – Y(b’), where b’ and b’’ are the horizontal bars of N*hor containing the bottom and top endpoint of segment e, respectively • Pro: linear complexity • Con: does not necessarily minimize edge length 41

Tidy vs. Fast-Rectangle-Compact 3 t 2 1 1 2 0 1 1 2 1 1 11 2 1 4 1 1 1 2 2 s 3 5 4 3 2 1 0 0 1 2 3 4 5 Total horizontal edge length = 22 5 5 4 3 2 1 0 42 0 1 2 3 4 5 Total horizontal edge length = 23

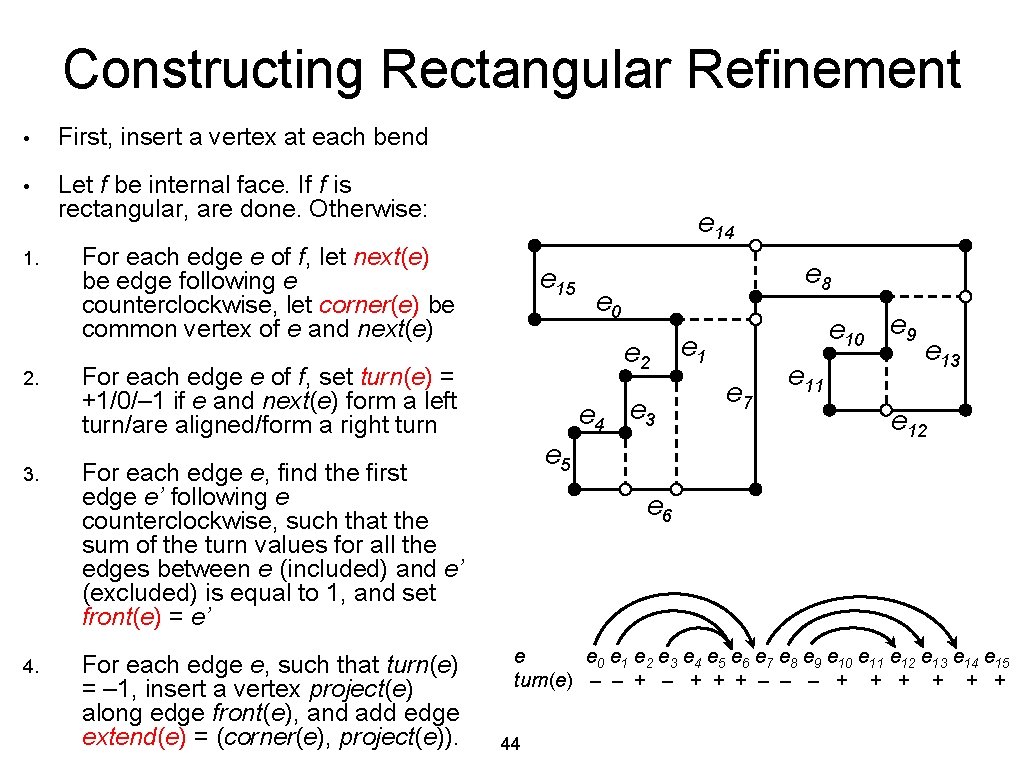
General Orthogonal Representations • So far, assumed faces to have rectangular shape • Now, generalize this by introducing “invisible” dummy edges • For graph G and orthogonal representation H, this results in rectangular refinement, which is orthogonal representation H’ of a graph G’ 43

Constructing Rectangular Refinement • First, insert a vertex at each bend • Let f be internal face. If f is rectangular, are done. Otherwise: 1. 2. 3. 4. e 14 For each edge e of f, let next(e) be edge following e counterclockwise, let corner(e) be common vertex of e and next(e) e 15 e 0 e 2 For each edge e of f, set turn(e) = +1/0/– 1 if e and next(e) form a left turn/are aligned/form a right turn e 4 e 3 e 5 For each edge e, find the first edge e’ following e counterclockwise, such that the sum of the turn values for all the edges between e (included) and e’ (excluded) is equal to 1, and set front(e) = e’ For each edge e, such that turn(e) = – 1, insert a vertex project(e) along edge front(e), and add edge extend(e) = (corner(e), project(e)). e 8 e 10 e 9 e 1 e 7 e 11 e 13 e 12 e 6 e e 0 e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 e 10 e 11 e 12 e 13 e 14 e 15 turn(e) – – + – + + + – – – + + + 44

Constructing Rectangular Refinement • For external face, proceed similarly • However, front(e) may not be defined for some edges • For those edges, add rectangle around external face, and project into that rectangle e 2 e 1 e 0 e 14 e 12 e 13 Combining this with Fast-Rectangle -Compact yields: Thm 5. 4: Given embedded planar graph G with n vertices of degree at most 4, and an orthogonal representation H of G with b bends, can construct planar orthogonal drawing of G with integer coordinates and area O((n + b)2) in O(n + b) time. e 8 e 11 e 10 45 e 6 e 15 e 9 e 7 e 5 e 4 e 3

Topology – Shape – Metrics [Paul Klose] Input: a graph G Algorithm: 1. Topology: Compute a good topological embedding of G 2. Shape: Compute a good orthogonal shape for this topological embedding 3. Metrics: Compute a good orthogonal grid drawing of G Output: an orthogonal grid drawing of G The following slides are based on material from Peter Eades 46

Use a maximum-planar-subgraph method 47

We need solutions for a difficult problem: Note � MPS is NP-complete � Many heuristic approaches have been investigated, implemented, and tested over at least the last 30 years The most successful approach to MPS so far is integer linear programming 48

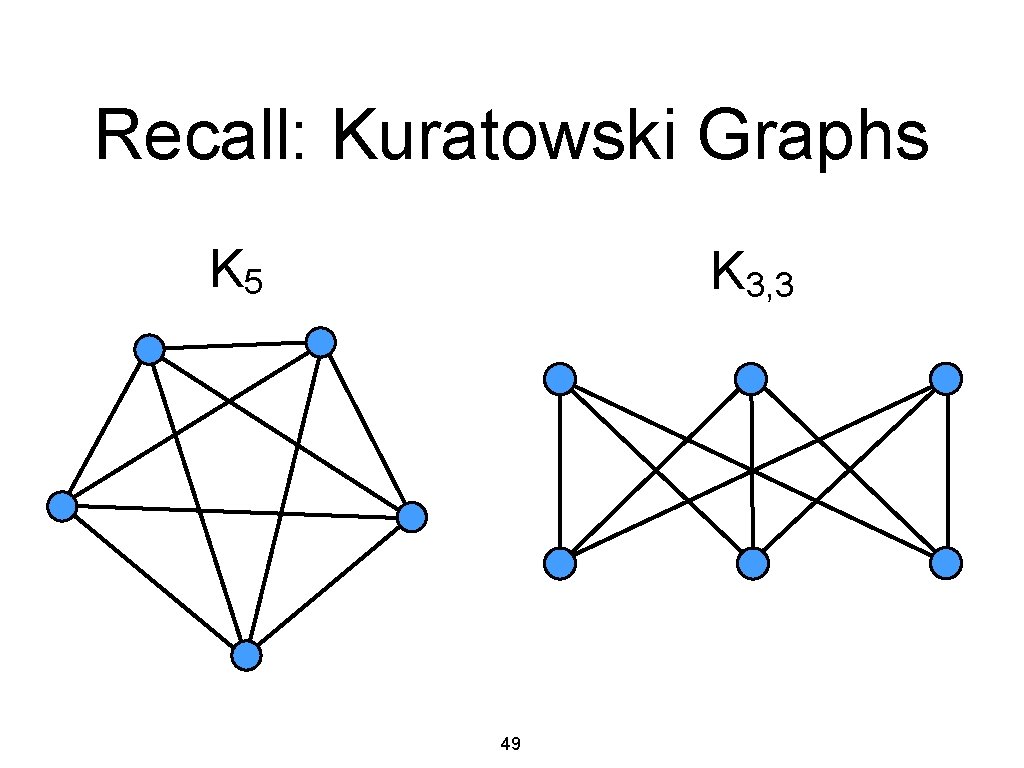
Recall: Kuratowski Graphs K 5 K 3, 3 49

50

Use planar embedding algorithms - For example, a variation on the Hopcroft-Tarjan planarity algorithm 51

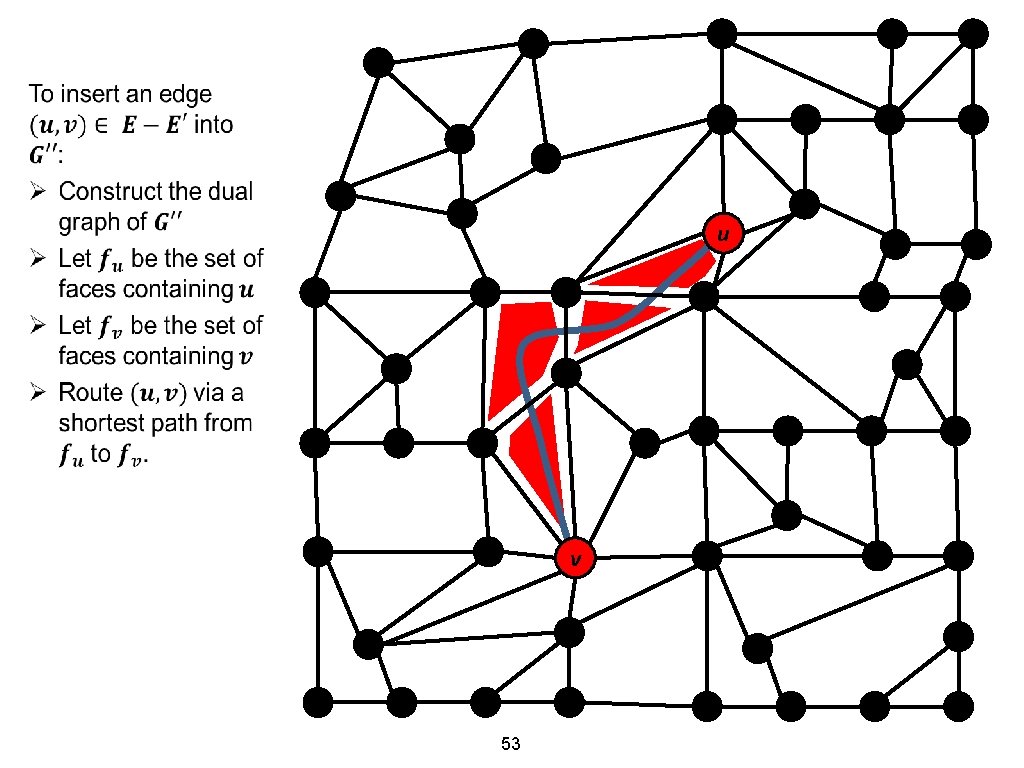
Use planar shortest path in the dual 52

0 1 2 6 7 8 5 8 6 5 4 0 u 1 2 5 8 4 4 1 0 1 2 3 3 6 2 7 8 4 6 7 5 0 1 v 3 5 8 0 4 6 7 53 1 3 5 8 2 4 6 7

54 Klein

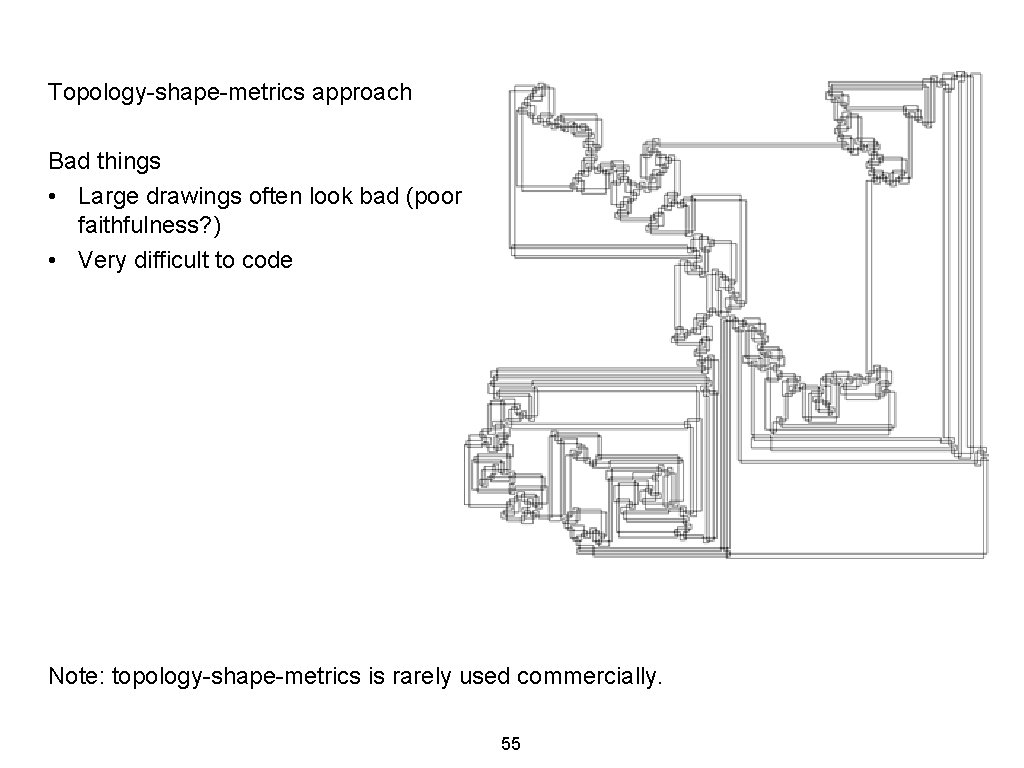
Topology-shape-metrics approach Bad things • Large drawings often look bad (poor faithfulness? ) • Very difficult to code Note: topology-shape-metrics is rarely used commercially. 55