Inferential Statistics Confidence Intervals and Hypothesis Testing Samples

Inferential Statistics Confidence Intervals and Hypothesis Testing

Samples vs. Populations • Population – All of the objects that belong to a class (e. g. all Darl projectile points, all Americans, all pollen grains) – A theoretical distribution • Sample – Some of the objects in a class – Observations drawn from a distribution

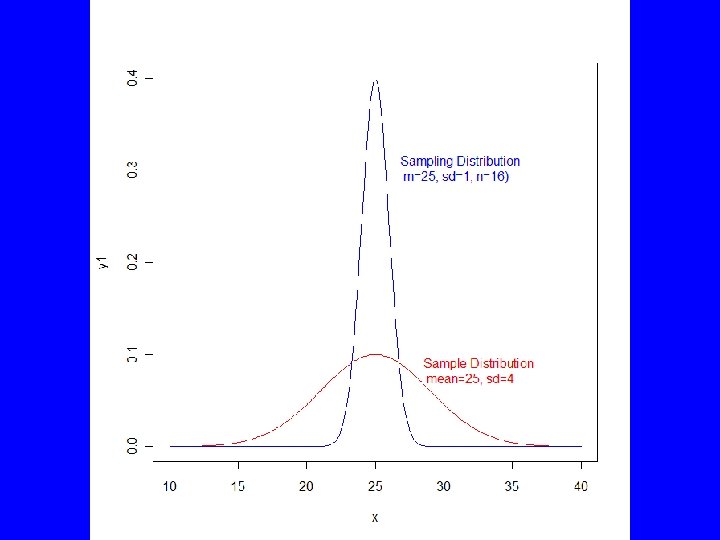
Two Distributions • The sample distribution is the distribution of the values of a sample – exactly what we get plotting a histogram or a kernel density plot • The sampling distribution is the distribution of a statistic that we have computed from the sample (e. g. a mean)

Confidence Intervals • Given a sample statistic estimating a population parameter, what is the parameter’s actual value? • Standard Error of the Estimate provides the standard deviation for the sample statistic:

Example 1 • Snodgrass house size. Mean area is 236. 8 with a standard deviation of 94. 25 based on 91 houses. • Area is slightly asymmetrical • Can we use these data to predict house sizes at other Mississippian sites?

Example 1 (cont) • The confidence interval is based on the mean, sd, and sample size • Mean ± t(p<confidence)*sd/sqrt(n) • For 95% , 90%, 67% confidence – qt(c(. 025, . 975), df=90) – qt(c(. 167, . 833), df=90)

# Distributions x <- seq(10, 40, length. out=200) y 1 <- dnorm(x, mean=25, sd=4) y 2 <- dnorm(x, mean=25, sd=1) max(y 2) plot(x, y 1, type="l", ylim=c(0, . 4), col="red") lines(x, y 2, col="blue") text(c(28, 26. 3), c(. 08, . 30), c("Sample Distributionn mean=25, sd=4", "Sampling Distributionn m=25, sd=1, n=16)"), col=c("red", "blue"), pos=4) # Snodgrass House Areas plot(density(Snodgrass$Area), main="Snodgrass House Areas") lines(seq(0, 475, length. out=100), dnorm(seq(0, 475, length. out=100), mean=236. 8, sd=94. 2), lty=2) abline(v=mean(Snodgrass$Area)) legend("topright", c("Kernel Density", "Normal Distribution"), lty=c(1, 2)) # Confidence interval function conf <- function(x, conf) { conf <- ifelse(conf>1, conf/100, conf) tail <- (1 -conf)/2 mean(x)+qt(c(tail, 1 -tail), df=length(x)-1)*sd(x)/sqrt(length(x)) }

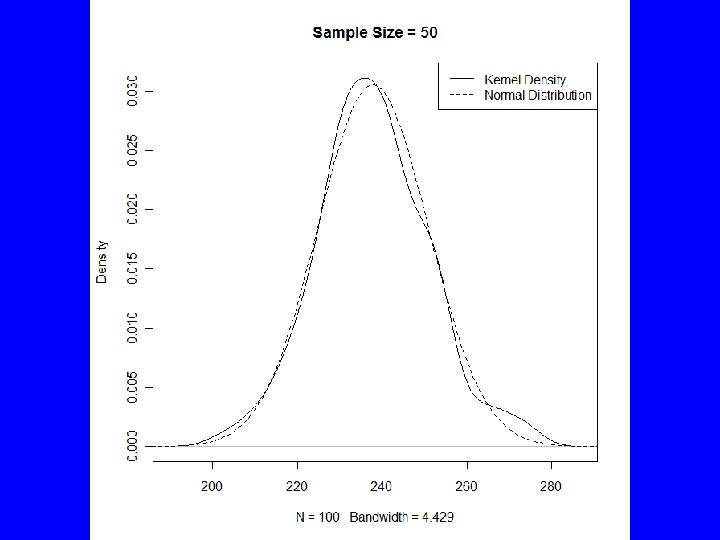
Bootstrapping • Confidence intervals depend on a normal sampling distribution • This will generally be a reasonable assumption if the sample size is moderately large • We can draw multiple samples of house areas to get some idea

# Draw 100 samples of size 50 samples <- sapply(1: 100, function(x) mean(sample(Snodgrass$Area, 50, replace=TRUE))) range(samples) quantile(samples, probs=c(. 025, . 975)) conf(Snodgrass$Area, 95) plot(density(samples), main="Sample Size = 50") x <- seq(175, 300, 1) lines(x, dnorm(x, mean=mean(samples), sd=sd(samples)), lty=2) legend("topright", c("Kernel Density", "Normal Distribution"), lty=c(1, 2)) # Draw 1000 samples of size 91 samples <- sapply(1: 100, function(x) mean(sample(Snodgrass$Area, 91, replace=TRUE))) range(samples) quantile(samples, probs=c(. 025, . 975)) conf(Snodgrass$Area, 95) plot(density(samples), main="Sample Size = 91") x <- seq(175, 300, 1) lines(x, dnorm(x, mean=mean(samples), sd=sd(samples)), lty=2) legend("topright", c("Kernel Density", "Normal Distribution"), lty=c(1, 2))

Example 2 • Radiocarbon Ages are presented as an age estimate and a standard error: 2810 ± 110 B. P. • The probability that the true age is between 2700 and 2920 B. P. is. 6826 or. 3174 that it is outside that range • The probability that the true age is between 2590 and 3030 B. P. is. 9546 or. 0545 that it is outside that range

Hypothesis Testing • • • Assumptions and Null Hypothesis Test Statistic (method) Significance Level Observe Data Compute Test Statistic Make Decision

Assumptions • Data are a random sample – Every combination is equally likely • Appropriate sampling distribution

Null Hypothesis • Represented by H 0 • Must be specific, e. g. S 1 -S 2 = 0 • The difference between two sample statistics is zero, e. g. they are drawn from the same population (two tailed test) • Or S 1 -S 2>0 (one tailed)

Test Statistic • • Measurement Levels Number of groups Dependent vs. Independent Power

Significance Level • Nothing is absolute in probability • Select probability of making certain kinds of errors • Cannot minimize both kinds of errors • Social scientists often use p ≤ 0. 05 • Consider how many tests

Errors in Hypothesis Testing Null Hypothesis (H 0) is Research Decision Reject H 0 Accept H 0 (fail to reject) True False Error Type I, α Correct Decision Error Type II, β

Difference of Means (t-test) • Independent random samples of normally distributed variates • Samples: 1, 2 independent, 2 related • If 2 independent – variances equal or unequal • Sample statistics follow the t-distribution

Example • Snodgrass site is a Mississippian site in Missouri that was occupied about A. D. 1164

Using Rcmdr • Snodgrass Site – House sizes inside and outside are the same • Check normality - shapiro. test() • Check equal variances – var. test() or bartlett. test() • Compute statistic and make decision – t. test()

Wilcoxon Test • If data do not follow a normal distribution or are ranks not interval/ratio scale • Nonparametric test that is similar to the t -test but not as powerful • Tests for equality of medians – wilcox. test()

Difference of Proportions • Uses the normal distribution to approximate the binomial distribution to test differences between proportions (probabilities) • This approximation is accurate as long as N x (min(p, (1 -p))>5 where N is the sample size, p is the proportion, and min() is the minimum

Using Rcmdr • Must have two or more variables defined as factors, eg, – Create Proj. Pts to be equal to as. factor(ifelse(Points>0, 1, 0)) using Data | Manage variables. . . | Compute new variable – Statistics | Proportions | Two sample. . . – prop. test() – Are the % Absent equal inside and outside the wall?