Inference on the Variance of a Normal Population

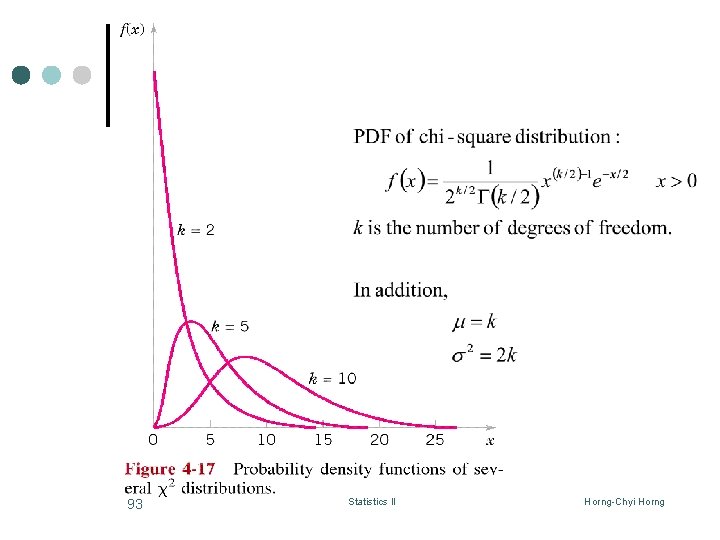
Inference on the Variance of a Normal Population (I) ¢ ¢ H 0 : s 2 = s 0 2 H 1: s 2 s 02 , where s 02 is a specified constant. Sampling from a normal distribution with unknown mean m and unknown variance s 2, the quantity has a Chi-square distribution with n-1 degrees of freedom. That is, 91 Statistics II Horng-Chyi Horng

Inference on the Variance of a Normal Population (II) ¢ Let X 1, X 2, …, Xn be a random sample for a normal distribution with unknown mean m and unknown variance s 2. To test the hypothesis H 0 : s 2 = s 0 2 H 1: s 2 s 02 , where s 02 is a specified constant. We use the statistic ¢ If H 0 is true, then the statistic has a chi-square distribution with n-1 d. f. . 92 Statistics II Horng-Chyi Horng

93 Statistics II Horng-Chyi Horng

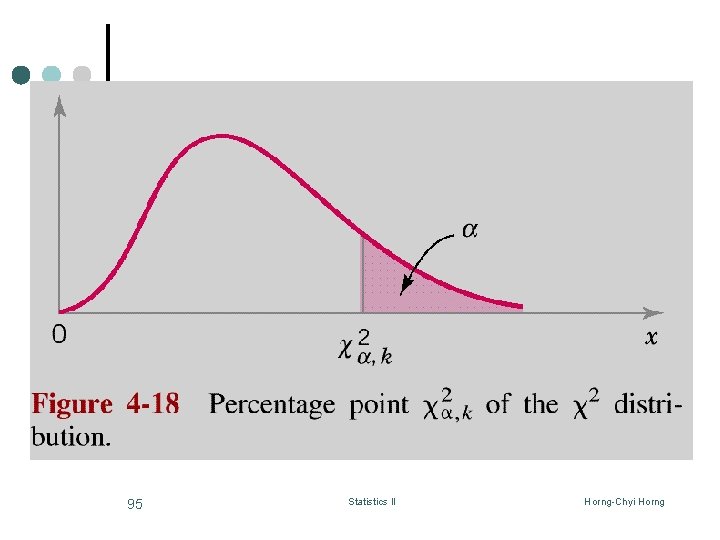
The Reasoning ¢ For H 0 to be true, the value of 02 can not be too large or too small. ¢ What values of 02 should we reject H 0? (based on a value) What values of 02 should we conclude that there is not enough evidence to reject H 0? 94 Statistics II Horng-Chyi Horng

95 Statistics II Horng-Chyi Horng

Example 8 -11 An automatic filling machine is used to fill bottles with liquid detergent. A random sample of 20 bottles results in a sample variance of fill volume of s 2 = 0. 0153 (fluid ounces)2. If the variance of fill volume exceeds 0. 01 (fluid ounces)2, an unacceptable proportion of bottles will be underfilled and overfilled. Is there evidence in the sample data to suggest that the manufacturer has a problem with underfilled and overfilled bottles? Use a = 0. 05, and assume that fill volume has a normal distribution. 96 Statistics II Horng-Chyi Horng

97 Statistics II Horng-Chyi Horng

Hypothesis Testing on Variance - Normal Population 98 Statistics II Horng-Chyi Horng

Finding P-Values ¢ Steps: 1. Find the degrees of freedom (k = n-1)in the 2 -table. 2. Compare 02 to the values in that row and find the closest one. 3. Look the a value associated with the one you pick. The p-value of your test is equal to this a value. ¢ In example 8 -11, 02 = 29. 07, k = n-1 = 19, 0. 05 < P-Value < 0. 10 because the 2 value associated with (k = 19, a = 0. 10) is 27. 20 while the 2 value associated with (k = 19, a = 0. 05) is 30. 14 99 Statistics II Horng-Chyi Horng

P-Values of Hypothesis Testing on Variance 100 Statistics II Horng-Chyi Horng

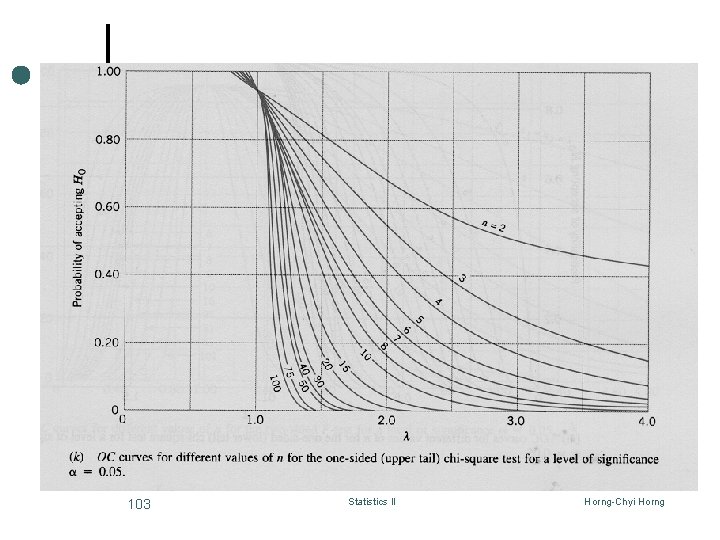
The Operating Characteristic Curves - Chi-square test ¢ Use to performing sample size or type II error calculations. The parameter l is defined as: ¢ for various sample sizes n, where s denotes the true value of the standard deviation. Chart VI I, j, k, l are used in chi-square test. (pp. A 16 -A 17) ¢ 101 Statistics II Horng-Chyi Horng

Example 8 -12 102 Statistics II Horng-Chyi Horng

103 Statistics II Horng-Chyi Horng

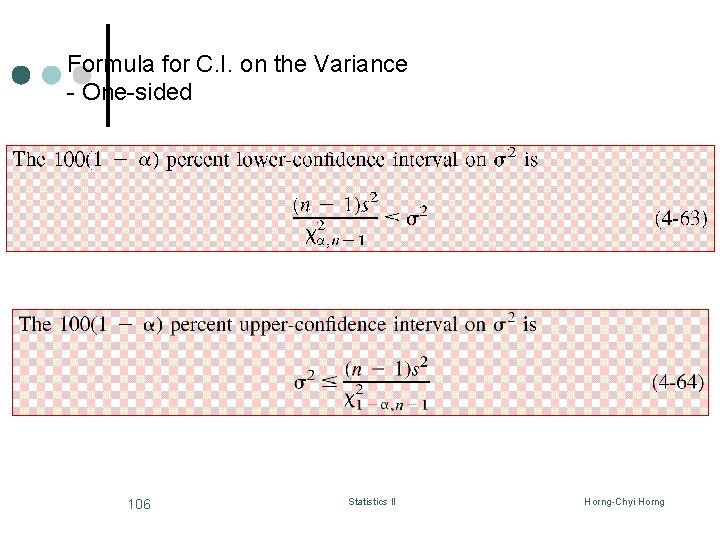
Construction of the C. I. on the Variance ¢ In general, the distribution of is chi-square with n-1 d. f. ¢ Use the properties of t with n-1 d. f. , 104 Statistics II Horng-Chyi Horng

Formula for C. I. on the Variance 105 Statistics II Horng-Chyi Horng

Formula for C. I. on the Variance - One-sided 106 Statistics II Horng-Chyi Horng

Example 8 -13 Reconsider the bottle filling machine problem in Example 811. Find a 95% upper-C. I. on the variance? ¢ N = 20, s 2 = 0. 0153 Therefore, s 2 (20 -1)0. 0153/10. 117 = 0. 0287 The 95% upper-C. I. on the variance is 0. 0287. In addition, the 95% upper-C. I. on the standard deviation is 0. 0287 = 0. 17. 107 Statistics II Horng-Chyi Horng

Inference on a Population Proportion(I) ¢ ¢ ¢ H 0: p = p 0 H 1: p p 0 , where p 0 is a specified constant. P = X/n, in which X is a binomial variable, i. e. , the number of success in n trials. E(X) = np, V(X) = npq = np(1 -p) If H 0 is true, then using the normal approximation to the binomial, the quantity follows the standard normal distribution(Z). 108 Statistics II Horng-Chyi Horng

Inference on a Population Proportion (II) ¢ Let x be the number of observations in a random sample of size n that belongs to the class associated with p. To test the hypothesis H 0: p = p 0 H 1: p p 0 , where p 0 is a specified constant. We use the statistic 109 Statistics II Horng-Chyi Horng

The Reasoning ¢ For H 0 to be true, the value of Z 0 can not be too large or too small. ¢ What values of Z 0 should we reject H 0? (based on a value) What values of Z 0 should we conclude that there is not enough evidence to reject H 0? 110 Statistics II Horng-Chyi Horng

Example 8 -14 A semiconductor manufacturing produces controllers used in automobile engine applications. The customer erquires that the process fallout or fraction defective at a critical manufacturing step not exceed 0. 05 and that the manufacturing demonstrate process capacity at this level of quality using a = 0. 05. The semiconductor manufacturer takes a random sample of 200 devices and finds that four of them are defective. Can the manufacturer demonstrate process capacity for the customer? 111 Statistics II Horng-Chyi Horng

¢ ¢ The parameter of interest is the process fraction defective. H 0: p = 0. 05 H 1: p < 0. 05 This formulation of the problem will allow the manufacturer to make a strong claim about process capacity if the null hypothesis H 0: p = 0. 05 is rejected. a = 0. 05, x = 4, n = 200, and p 0 = 0. 05. To reject H 0: p = 0. 05, the test statistic Z 0 must be less than -z 0. 05 = -1. 645 ¢ ¢ Conclusion: Since Z 0 = -1. 95 < -z 0. 05 = -1. 645, we reject H 0 and conclude that the process fraction defective p is less than 0. 05. The P-value for this value of the test statistic Z 0 is P = 0. 0256, which is less than a = 0. 05. We conclude that the process is capable. 112 Statistics II Horng-Chyi Horng

Hypothesis Testing on a Population Proportion 113 Statistics II Horng-Chyi Horng

P-Values of Hypothesis Testing on a Population Proportion 114 Statistics II Horng-Chyi Horng

How to calculate Type II Error? (I) (H 0: p = p 0 Vs. H 1: p p 0) ¢ 115 Under the circumstance of type II error, H 0 is false. Supposed that the true value of the population proportion is p. The distribution of Z 0 is: Statistics II Horng-Chyi Horng

How to calculate Type II Error? (II) - refer to section &4. 3 (&8. 1) ¢ Type II error occurred when (fail to reject H 0 while H 0 is false) ¢ Therefore, 116 Statistics II Horng-Chyi Horng

Formula for Type II Error ¢ Two-sided alternative H 1: p p 0 ¢ One-sided alternative H 1: p < p 0 ¢ One-sided alternative H 1: p > p 0 117 Statistics II Horng-Chyi Horng

The Sample Size (I) ¢ 118 Given values of a and p, find the required sample size n to achieve a particular level of b. Statistics II Horng-Chyi Horng

The Sample Size (II) ¢ ¢ Two-sided Hypothesis Testing One-sided Hypothesis Testing 119 Statistics II Horng-Chyi Horng

Example 8 -15 (1) Consider the semiconductor manufacturer from Example 8 -14. Suppose that his process fallout is really p = 0. 03. What is the b-error for his test of process capacity, which uses n = 200 and a = 0. 05? (2) Suppose that the semiconductor manuafcturer was willing to accept a b-error as large as 0. 10 if the true value of the process fraction defective was p = 0. 03. If the manufacturer continue to use a = 0. 05, what sample size would be required? 120 Statistics II Horng-Chyi Horng

(1) Since H 1: p < 0. 05, therefore (2) The sample size required for this one-sided alternative is 121 Statistics II Horng-Chyi Horng

Formula for C. I. on the Population Proportion 122 Statistics II Horng-Chyi Horng

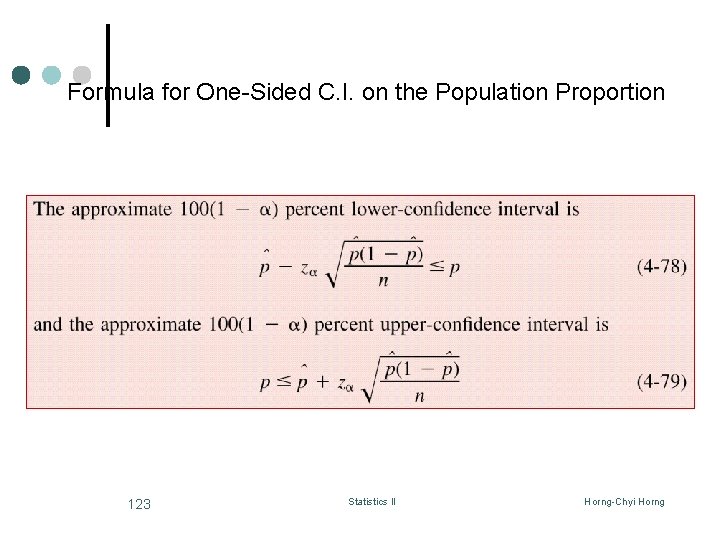
Formula for One-Sided C. I. on the Population Proportion 123 Statistics II Horng-Chyi Horng

Example 8 -16 In a random sample of 85 automobile engine crankshaft bearings, 10 have a surface finish that is rougher than the specifications allow. Construct a 95% C. I. on the population proportion p? Sol: 124 Statistics II Horng-Chyi Horng

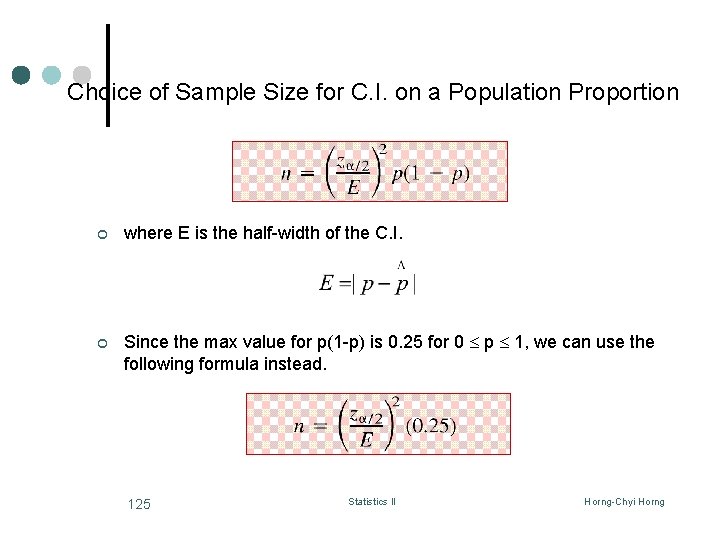
Choice of Sample Size for C. I. on a Population Proportion ¢ where E is the half-width of the C. I. ¢ Since the max value for p(1 -p) is 0. 25 for 0 p 1, we can use the following formula instead. 125 Statistics II Horng-Chyi Horng

126 Statistics II Horng-Chyi Horng