Inertial Navigation System INS Introduction to INS INS

Inertial Navigation System (INS)

Introduction to INS • INS is a navigation aid that uses a computer, motion sensors and rotation sensors. • The motion sensors such as accelerometers. • The rotational sensors such as gyroscopes. • It calculates the position, orientation, and velocity of a moving object. • Inertial navigation is a self-contained navigation technique. • The INS is initially provided with its position and velocity from another source such as: GPS satellite receiver, etc. • It is the only form of navigation that does not depend on external references. • It is used on vehicles such as ships, aircraft, submarines, guided missiles, and spacecraft.

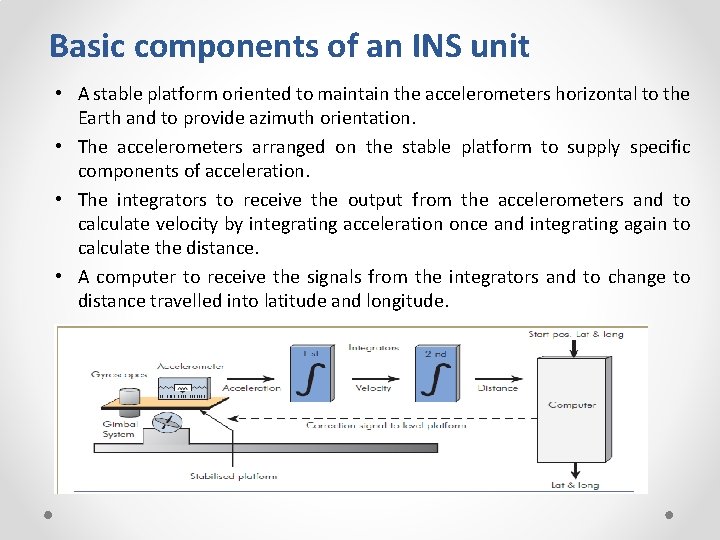
Basic components of an INS unit • A stable platform oriented to maintain the accelerometers horizontal to the Earth and to provide azimuth orientation. • The accelerometers arranged on the stable platform to supply specific components of acceleration. • The integrators to receive the output from the accelerometers and to calculate velocity by integrating acceleration once and integrating again to calculate the distance. • A computer to receive the signals from the integrators and to change to distance travelled into latitude and longitude. • .

Accelerometers • The basic principles upon which the accelerometers operate are related to Newton's laws regarding motion. • Linear accelerometers measure object’s linear acceleration and therefore detect direction of object’s movement. • Most accelerometers are able to measure acceleration along one axis. • In an inertial navigation system, two or three accelerometers are used. • One will measure the aircraft’s accelerations in the North-South directions. • Second one will measure the aircraft’s accelerations in the East-West directions. • The third accelerometer, if fitted, will measure vertical displacement.

Gyroscopes • • • Gyroscopes are rotational sensors that measure the angular velocity or orientation of a device. Gyros can be used as rate gyros or integrating gyros. There are different types of gyroscopes such as : Mechanical, Optical and MEMS gyroscopes. Ø Mechanical gyroscope • A conventional gyroscope consists of a spinning wheel mounted on two gimbals which allow it to rotate in all three axes. • Conventional gyroscope measures orientation. Ø • • Disadvantages of Mechanical gyroscopes It contains moving parts. Moving parts cause friction, which in turn causes the output to drift over time. To minimize friction high-precision, bearings and special lubricants are use. Mechanical gyroscopes also require a few minutes to warm up, which is not ideal in many situations.

Optical gyroscope • It uses the interference of light to measure angular velocity. • Define Sagnac effect. • Difference between a fiber optical gyroscopes and Ring laser gyroscopes. Ø Advantages of OFG over Mechanical gyroscope • Optical gyros contain no moving parts. • Requires only a few seconds to start-up. • The accuracy of an optical gyro is largely dependent on the length of the light transmission path (larger is better).

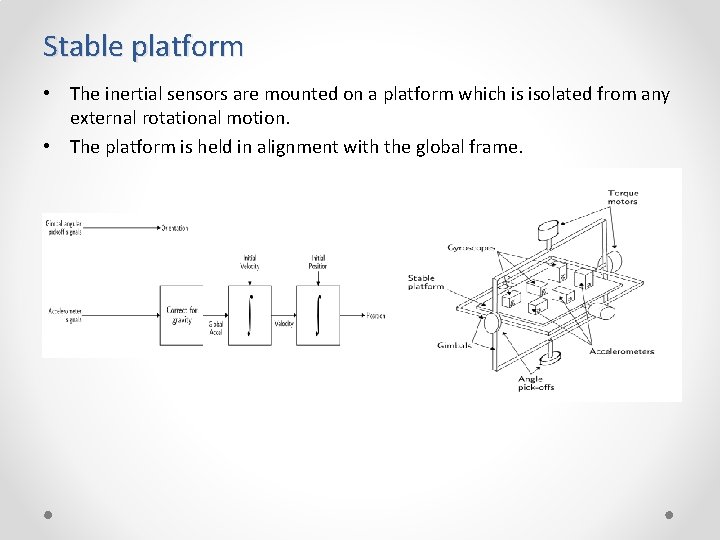
Stable platform • The inertial sensors are mounted on a platform which is isolated from any external rotational motion. • The platform is held in alignment with the global frame.

Strapdown Systems • The inertial sensors are mounted rigidly onto the device. • Output quantities measured in the body frame rather than the global frame. Ø • • Benefits of this approach Strapdown systems have reduced the mechanical complexity. Physically smaller than stable platform systems. Not expensive. Due to its benefits Strapdown systems have become the dominant type of INS.

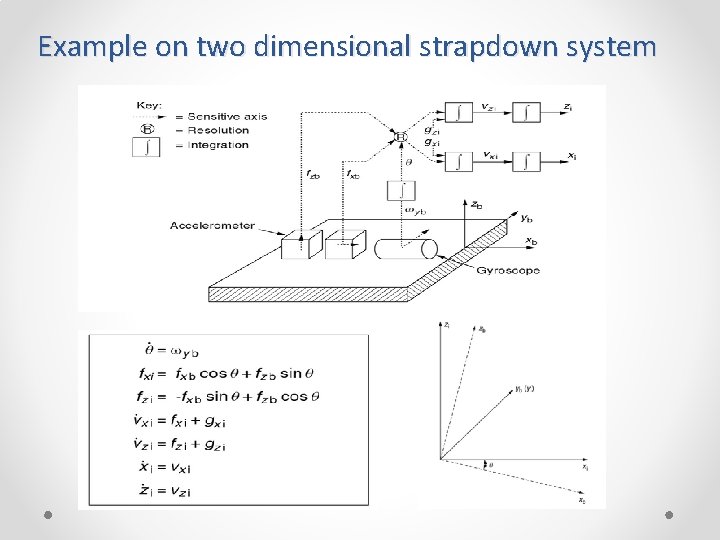
Example on two dimensional strapdown system

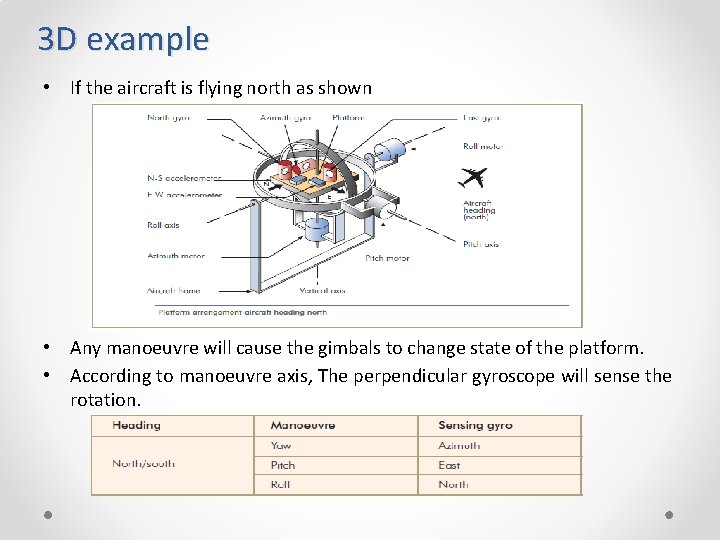
3 D example • If the aircraft is flying north as shown • Any manoeuvre will cause the gimbals to change state of the platform. • According to manoeuvre axis, The perpendicular gyroscope will sense the rotation.

Flight Dynamics and Controls (FDC) • It’s a toolbox that takes as an input the initial conditions of the aircraft and gave as its output the time history of the aircraft in the form of a state vector X. Ø Φ, θ, Ψ: Are the Euler angles in radians. Ø P, q, r: Are the roll, pitch and yaw rates from the gyroscopes in radians per second. Ø ax, ay, az: Are the accelerations from the accelerometers in m/s^2. Ø X, Y, Z: Are the distances along the three axes in the navigation frame in meters. Ø VT, α, β: Are the velocity of the aircraft in m/s, the angle of attack in radians and the sideslip angle in radians, respectively. • The FDC program can generate these values at any time step as required.

Calculations of initial and updated Euler parameters • The initial Euler parameters are calculated from the following equations: • While the updated Euler parameters are calculated from the following equations:

Calculations of updated Euler angles • The INS computer system calculates the updated Euler angles using the following equations: • Θ: Pitch angle that occurs when aircraft makes a rotation about the pitch axis. • Φ: if the rotation occurs about the roll axis and its called the bank angle. • Ψ: if the rotation occurs about the yaw axis.

Acceleration, Velocity and position calculations • Acceleration can be calculated using these equations: • The initial values of U, V, W can be calculated using: • The above values initially taken from FDC state vector at time t=0. • The acceleration equations are then integrated to get updated values of U, V and W. • The earth is rotating in space at a rate Ω (15 degrees per hour) around an axis South to North. • The motion of a vehicle at a constant height above the ground will induce an additional rotation due to earths rotation.

Acceleration, Velocity and position calculations • DCM is the transformation matrix, from the local earth or navigation frame to the body frame. • It transforms velocity components using the direction cosine matrix to give velocity along North (VN), velocity along East (VE) and downward velocity (VD) in the navigation frame or local earth frame.

Latitude, Longitude and Height of aircraft • VN, VE and VD are then integrated to give distances moved along the navigation axes X, Y and Z on the surface of the earth. • λ denotes to the latitude and its rate of change can be calculated using • μ denotes to the longitude and its rate of change can be calculated using • H denotes to the height of the aircraft at any instant and its rate of change is given by: • Re is the radius of the earth.

Errors in the INS • Most INS errors are attributed to the inertial sensors (instrument errors). • The dominant error sources are shown in the following table:

Errors in the INS • Navigation errors are errors in the accelerations and angular rates lead to growing errors in position and velocity components of the aircraft, due to integration. • These errors are nine : three position errors, three velocity errors, two attitude errors and one heading error. • Gravity model can also cause some errors. • If an unaided INS is used, these errors grow with time so, this is the reason that the INS is usually aided with other aided system such as: GPS.

INS Alignment • Alignment is the process whereby the orientation of the axes of an inertial navigation system is determined with respect to the reference axis system. • Accurate alignment is crucial, however, if precision navigation is to be achieved over long periods of time without any form of aiding. • In many applications, it is essential to achieve an accurate alignment of an inertial navigation system within a very short period of time. • To the determination of initial attitude, it is necessary to initialize the velocity and position defined by the navigation system as part of the alignment process. • There are two fundamental types of alignment process: 1. Self-alignment, using gyrocompassing techniques 2. The alignment of a slave system with respect to a master reference • There are various systematic and random errors that limit the accuracy to which an INS can be aligned.

INS Alignment basic principle • The inertial system to be aligned contains an instrument cluster. • Gyroscopes and accelerometers are arranged to provide three axes of angular rate information and three axes of specific force data in three directions, which are usually mutually perpendicular. (operational slides) • The sensitive axes of the gyroscopes are physically aligned with the accelerometer axes. • The alignment process involves the determination of the orientation of the orthogonal axis set. • The accelerometer input axes with respect to the designated reference frame.

Alignment on fixed platform • It is a system which required to align an inertial navigation system to the local geographic co-ordinate frame defined by the directions of true north and the local vertical. • The accelerometers measure three orthogonal components of the specific force needed to overcome gravity. • The gyroscopes measure the components of the Earth’s turn rate in the same directions. • In a platform mechanization, alignment is achieved by adjusting the orientation of the platform until the measured components of specific force and Earth’s rate become equal to the expected values. • The instrument cluster is rotated until the outputs of the north and east accelerometers reach a null, thus levelling the platform. • The platform is then rotated about the vertical until the east gyroscope output is nulled, thus achieving an alignment in azimuth.

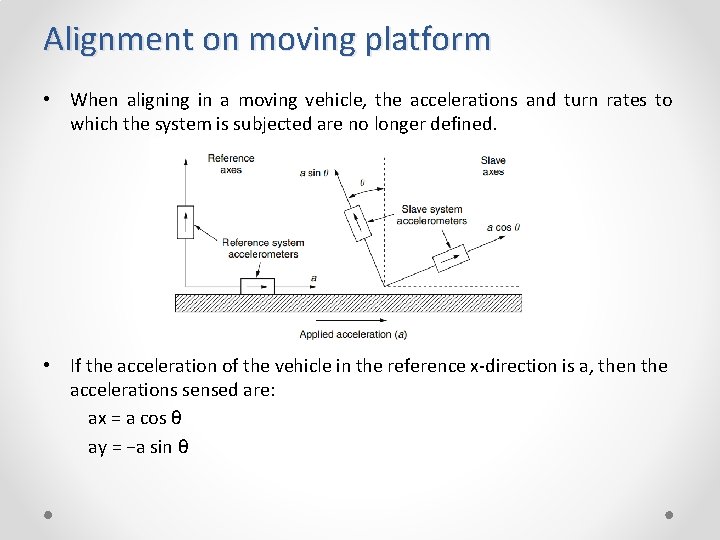
Alignment on moving platform • When aligning in a moving vehicle, the accelerations and turn rates to which the system is subjected are no longer defined. • If the acceleration of the vehicle in the reference x-direction is a, then the accelerations sensed are: ax = a cos θ ay = −a sin θ

Alignment on moving platform • Alignment of the system may be achieved by resolving the accelerometer measurements through an angle θ’. ax cos θ’ − ay sin θ’ = a ax sin θ’ + ay cos θ’ = 0 Substituting for ax and ay from eqn. in the previse slide: a cos(θ − θ’ ) = a a sin(θ − θ’ ) = 0 It can be seen that these relationships will be satisfied when θ’ = θ. • Therefore, it is possible to determine the orientation of the sensors by comparing the accelerometer measurements resolved into the reference frame with independent measurements of these same quantities. • Alignment may be achieved by comparing estimates of velocity or position generated with similar estimates provided by an external source over a period of time which is used in In-flight system.

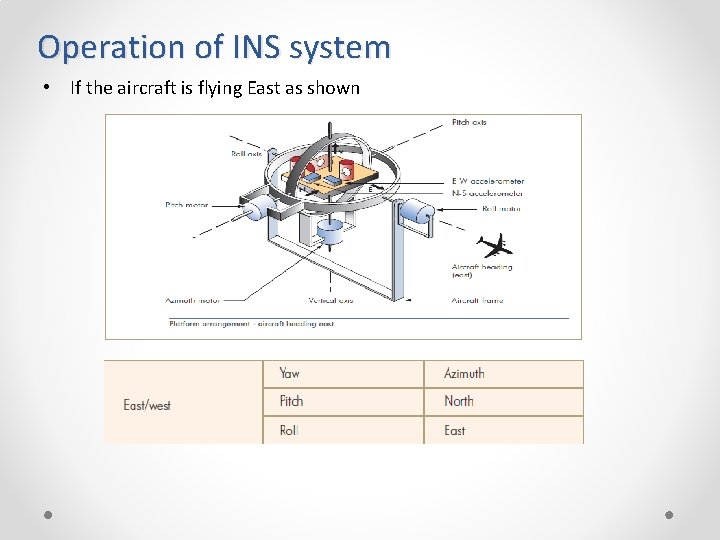
Operation of INS system • If the aircraft is flying East as shown

Digital mobile mapping • Mobile mapping is the method of collecting geospatial information from a moving vehicle. • Mobile mapping vehicles collect data to map features along the route using a range of imaging sensors. • The accuracy, precision and frequency of measurements that are required to be mapped. • The system needs to be able to collect data in such a way that users are able to locate and position features of interest in data collected by the mobile mapping vehicle. • These data not only requires knowledge of where the vehicle is located, but also the orientation and onward velocity of the vehicle. • Survey technologies such as GPS are well known and widely used, but relying only upon GPS will lead to incomplete mobile mapping results.

Digital mobile mapping • In practice, mobile mapping is best undertaken when a range of sensors are being used to locate the position, direction and orientation of the vehicle, while it is moving. • These additional sensors help fill in the gaps when a location is unknown, and usually include: 1. GPS receivers, for calculating latitude, longitude and elevation 2. An odometer, for measuring distance travelled 3. An inertial measurement unit (IMU), for measuring roll, pitch and heading of the vehicle and the sensors upon it. 4. A computer processing unit containing various statistical algorithms for predicting the position of the mobile mapping vehicle, based upon the accumulated readings from the sensors described above.

Digital mobile mapping • INS is the computational system that includes an IMU, and takes input from the GPS and odometer systems (when available) to calculate the overall most likely position of the vehicle. • The hardware component that provides much of the information related to the dynamics of the mobile mapping vehicle’s motion is the IMU. • The IMU will provide a continuous stream of data related to the linear acceleration of the vehicle on three axes, together with the three sets of rotation parameters. • The integrators as a processing unit on the INS; algorithms will be applied that check and analyze the input data from the sensors connected to the GPS. • Using statistical algorithms such as Kalman filters, absolute positions and orientations data will be calculated based upon all of the information available at each instance in time. • The INS system enables the mobile mapping system to continuously collect information data.

Ø Advantages of INS • It requires no external references in order to determine its position, orientation, or velocity once it has been initialized. • It is immune to jamming and deception since it requires no external reference after initialization. • It displays the aircraft velocity and position in real-time. • It operates at all the altitudes. Ø Disadvantages of INS • • Integration drift. Errors are generated by non orthogonality of accelerometers. Vibration and thermal variation may cause flaws in information data. INS is an expensive technology.

Why INS-GPS integration? ? § Most Navigation systems need to haveo Continuous and Reliable Navigation determination( Position and Orientation) o Acceptable Accuracy level and possibility of maintaining it over time § GPS and INS integration advantageso Their Error Dynamics are totally different and uncorrelated. o GPS solves the problem of “calibrating” the instrument errors in a strapdown INS. o GPS provides a means of “in-flight” alignment for all INS. o The I. N. provides a means of smoothing the noisy velocity outputs from the GPS, and a continuous high bandwidth measurement of position and velocity. o In a tightly integrated system, the I. N. provides a means for narrowing the bandwidth of the GPS tracking loops, providing greater immunity to jamming. 29

Inertial and gps attributes and shortcomings 30

ACCURACY • The position calculated by a GPS receiver relies on three accurate measurements: o Current time o Position of the satellite o Time delay for the signal • The GPS signal in space will provide a "worst case" accuracy of 7. 8 meters at a 95% confidence level. • GPS time is accurate to about 14 nanoseconds. • Higher accuracy is available today by using GPS in combination with augmentation systems. These enable real-time positioning to within a few centimeters.

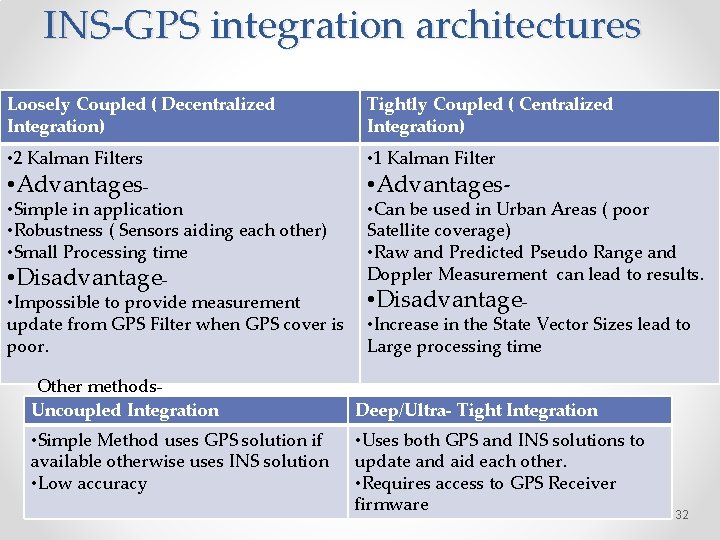
INS-GPS integration architectures Loosely Coupled ( Decentralized Integration) Tightly Coupled ( Centralized Integration) • 2 Kalman Filters • Advantages • Simple in application • Robustness ( Sensors aiding each other) • Small Processing time • Disadvantage • Impossible to provide measurement update from GPS Filter when GPS cover is poor. • 1 Kalman Filter Other methods. Uncoupled Integration • Simple Method uses GPS solution if available otherwise uses INS solution • Low accuracy • Advantages- • Can be used in Urban Areas ( poor Satellite coverage) • Raw and Predicted Pseudo Range and Doppler Measurement can lead to results. • Disadvantage • Increase in the State Vector Sizes lead to Large processing time Deep/Ultra- Tight Integration • Uses both GPS and INS solutions to update and aid each other. • Requires access to GPS Receiver firmware 32

loosely coupled approach 33

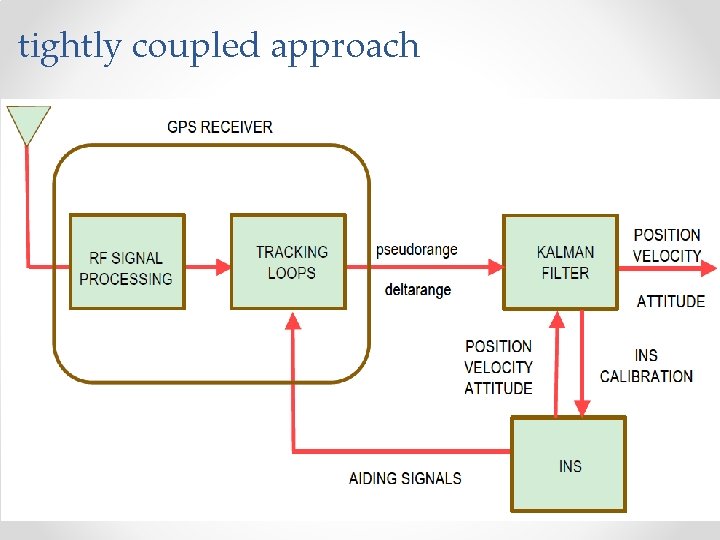
tightly coupled approach 34

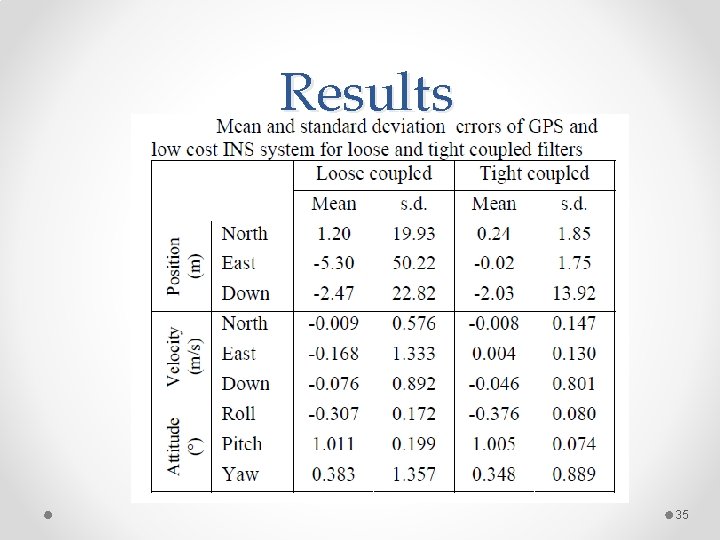
Results 35

SOURCES OF GPS SIGNAL ERRORS. • Different errors can cause a deviation of +/- 50 -100 meters from the actual GPS receiver position which are : • 1. Satellite clock : • One nano second of inaccuracy in a satellite clock results in about 30 cm • (1 foot) of error in measuring the distance to that satellite. • 2. Receiver clock : • Any error in the receiver clock causes inaccuracy in distance measurement. • However it is not practical to equip receiver with very accurate atomic clocks. Atomic clocks weigh more than 20 kgs, cost about US$ 50, 000. 3. GPS Jamming : o It limits the effectiveness of the GPS signal. o GPS jammer is a low cost device to temporarily disable the reception of the civilian coarse acquisition (C/A) code. o

Advantages of Post Processing Applications that can be benefitted/use Post processing to find positional solutions • Surveying Application like Inventory Management • Terrestrial Geo-referencing applications like Photogrammetric Surveying, Laser Scanning • Vehicle Performance Testing- Racing Cars or Product Testing • Surveillance- Commodity/ Vehicle Tracking • Road User- Charging where high accuracy is required and non availability of GPS service ( Urban Areas) 37

Kalman Filter • A linear quadratic state estimator. • Operates recursively on streams of noisy measurements to produce a optimal estimate of the state. • Prediction: Prediction of the current state based on previous state • Correction: After availability of measurement correction is made using a weighted average, with more weight being given to estimates with high error • Kalman Filter–The Work Horse for Integrated Navigation • A key function performed by the Kalman filter is the statistical combination of external (non-inertial) information and INS information to track or contained rifting parameters of the sensors in the INS. 38

Kalman filtering • The filter has its origin in a Kalman’s document (1960) where it is described as a recursive solution for the linear filtering problem for discrete data. The research was in a wide context of state – space models, where the point is the estimation through the recursive least squares. Since that moment, due to the development of digital calculation, Kalman filter has been researched and applied, particularly in self and assisted navigation, missiles search and economy. The study of Kalman filter is based on Wiener filter. • The filter is a mathematical procedure which operates through a prediction and correction mechanism. In essence, this algorithm predicts a new state from its previous estimation by adding a correction term proportional to the predicted error. In this way, this error is statistically minimized. • A Kalman filter is simply an optimal recursive data processing algorithm

Kalman Filter Smoothing Algorithm • It is basically a post processing algorithm to find out the position solutions after all the data has been collected. • 3 basic types of Smoothening Filters • Fixed Interval estimates the states at each of the points in a data set when all the data have been collected • Fixed Point used to estimate a specific point in a dataset • Fixed Lag can be applied in near real-time. 40

Implementation • The all pole, or autoregressive (AR), signal model is often used for speech. The AR signal model is introduced as: • Above equation can also be written in this form as shown below:

Cont… • In order to apply Kalman filtering to the speech expression shown above, it must be expressed in state space form as

Cont… • The Kalman filter functions in a looping method here we denote the following steps within the loop of the filter. Define matrix HTk-1 as the row vector and zk = yk where Xk will always be updated according to the number of iterations, k.

Kalman Filter 1. Computing the KALMAN GAIN K=P-k. HT(HP-k. HT+R)-1 q K, the Kalman gain(How much to trust this sensor) q P-k, as before, the Predicted Error Covariance q H, the model of how Sensor readings reflect the vehicle state – a function to go from Sensor Reading to STATE VECTOR q R describes the noise in Sensor Measurement

Advantages of Kalman Filter • Below are some advantages of the Kalman filter, comparing with another famous filter known as the Wiener Filter. 1. The Kalman filter algorithm is implementable on a digital computer, which this was replaced by analog circuitry for estimation and control when Kalman filter was first introduced. 2. Stationary properties of the Kalman filter are not required for the deterministic dynamics or random processes. Many applications of importance include non-stationary stochastic processes.

Cont… 3. 4. 5. The Kalman filter is compatible with state-space formulation of optimal controllers for dynamic systems. It proves useful towards the 2 properties of estimation and control for these systems. The Kalman filter requires less additional mathematical preparation to learn for the modern control engineering student. Necessary information for mathematically sound, statistically-based decision methods for detecting and rejecting anomalous measurements are provided through the use of Kalman filter.

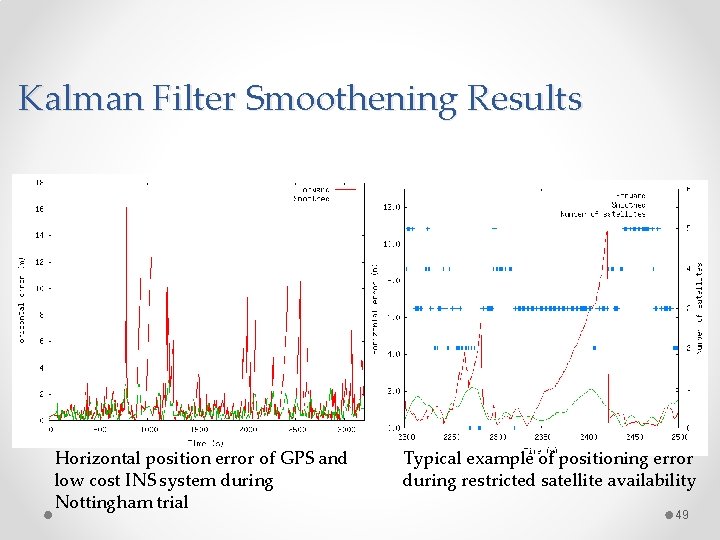
Fixed Interval Algorithm Advantage of Kalman filter smoothing during GPS outage (adapted from Gelb, 1977) When the forward and backward position estimates are computed, the INS position error quickly increases over time which is particularly so for systems that use a low cost INS. When the Kalman filter smoothing algorithm is applied to the data, the error is significantly reduced across the data outage interval. 47

For near Real- Time cases • Rauch- Tung- Striebel (RTS) algorithm can be used in near-real time by running the smoothing algorithm on short periods of data throughout during the data collection. Ex- For example, after every significant GPS outage, the algorithm could be applied once GPS availability returns. • Advantages- The RTS algorithm greatly reduces the computational effort required for Kalman filter smoothing since it only requires the full Kalman filter to be implemented in the forward direction. • Limitations- when carrier phase ambiguity states are modelled, the INS will not have the advantage of using fixed ambiguity GPS measurements that may have been resolved if a full reverse filter implementation were to have been implemented. 48

Kalman Filter Smoothening Results Horizontal position error of GPS and low cost INS system during Nottingham trial Typical example of positioning error during restricted satellite availability 49

Conclusions • It is clear from the results discussed that GPS and low cost INS integrated systems can meet the performance levels required for a number of applications, particularly in Urban Areas. • The benefit of post-processing the data is substantial. This can be utilised in many navigational purposes with limited GPS availability. 50