Inertia Weight Free fall Terminal velocity Chapter 12

• Inertia • Weight • Free fall • Terminal velocity Chapter 12 Motion (page 41) • Projectile motion • Momentum • Law of conservation of momentum • Newton's 1 st law • Newton's 2 nd law • Newton's 3 rd law

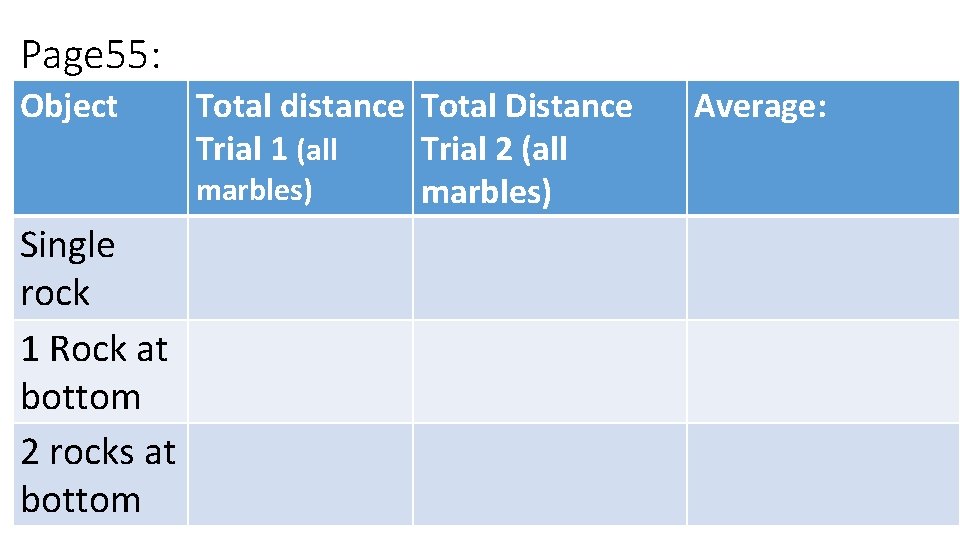
Page 55: Object Single rock 1 Rock at bottom 2 rocks at bottom Total distance Total Distance Trial 1 (all Trial 2 (all marbles) Average:

In the first part of the experiment what was the action reaction pair of forces? Page 54 How did the total distance in all the trials compare? How did the total movement of all the rocks change with changes in number of rocks and spacing?

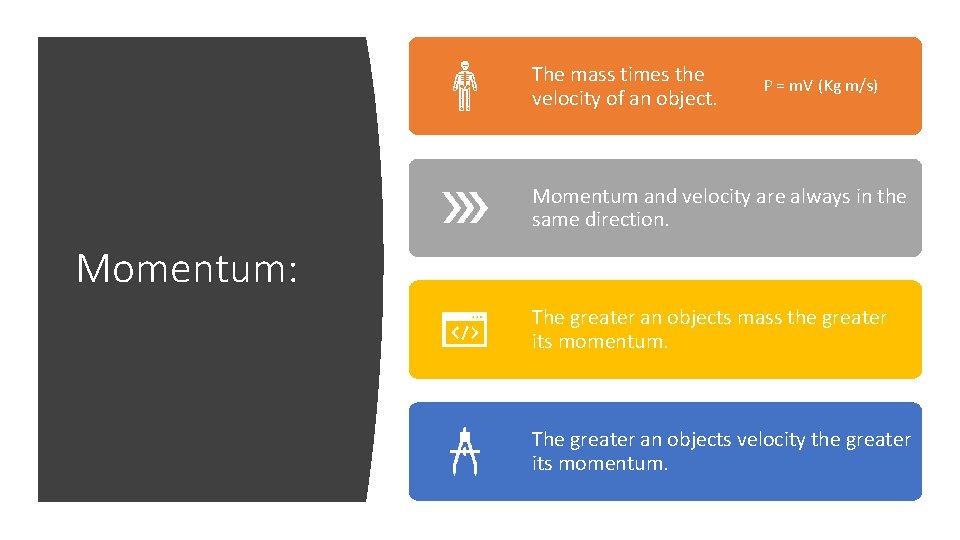
Momentum Page 57

Essential question • How can a running back increase his momentum, to make him harder to tackle?

The mass times the velocity of an object. P = m. V (Kg m/s) Momentum and velocity are always in the same direction. Momentum: The greater an objects mass the greater its momentum. The greater an objects velocity the greater its momentum.

Momentum: • Examples: • Bowling ball versus baseball • Klayton Kershaw verses me.

The total amount of momentum in an isolated system is always conserved. Conservation of momentum: The total momentum before the collision is equal to the total momentum after the collision. Newton’s third law explains conservation of momentum. Examples: Bumper cars billiard balls.

Math example: • Calculate the momentum of a 6. 00 kg bowling ball as it travels 10. 0 m/s down the alley towards the pins. • P= • m= • v=

Describe how momentum is calculated. Page 56: Momentum Questions Explain why it hurts more to get hit by a baseball then by a Ping-Pong ball moving at the same velocity. Why is a car crash worse if the 2 vehicles are going in opposite directions as apposed to the same direction? What is the momentum of a 2000 Kg boulder sitting on the side of the trail?

Page 43: Inertia Lab • Write all instructions first. • Copy the chart from below on page 43. • 1 person from the group, get 8 dominos and a ruler from the front. • another person from the group get 3 books from the front • Each team member will attempt to shoot the bottom domino into the books with out knocking the stack over. You may adjust the stack after each attempt. If the dominos fall your turn is over. Team Member Number of Successful shots

Page 42: Inertia Lab questions 1)When a shot was successful, why did the dominos not fall? 2)When a shot was unsuccessful, why did the dominos fall? 3)What is Newton's first law of motion?

Newton’s st 1 Page 45 & nd 2

Essential Question: • Why is Newton’s 1 st law of motion sometimes called the law of inertia?

Newton’s 1 st law: • An object at rest remains at rest and an object in motion maintains its velocity unless it experiences a net force. • Examples: Bowling ball, baseball, turning car. • Inertia: the tendency of an object to resist any change in motion. • All matter resists any change in motion.

Newton’s 2 nd Law of motion • The unbalanced force acting on an object is equal to the objects mass times its acceleration. • F = ma • If an equal force is applied to 2 different masses the larger mass will accelerate less. • Force is measured in Newton's (N).

Newton’s 2 nd Law of motion • Acceleration depends on force and mass. • Example pushing a car. • Example math: • What is the force of a 1, 600 Kg car accelerating at a rate of 2. 0 m/s 2? F= m= a=

Give 2 example of Newton’s 2 nd law. Explain how the law of inertia relates to seatbelts. LSA: page 44. 1 st and 2 nd Law questions. Predict what will happen when a car tries to turn on an icy road. A ball accelerates downward at 9. 8 m/s 2. If the gravitational force is 1. 4 N, what is the mass of the ball? The net force on the propeller of a 3. 2 Kg model plane is 7. 0 N. What is the acceleration of the airplane? What is the force is needed to accelerate a 10 Kg bowling ball forward at 5. 0 m/s 2?

Page 51. Projectile Lab 1 2 3

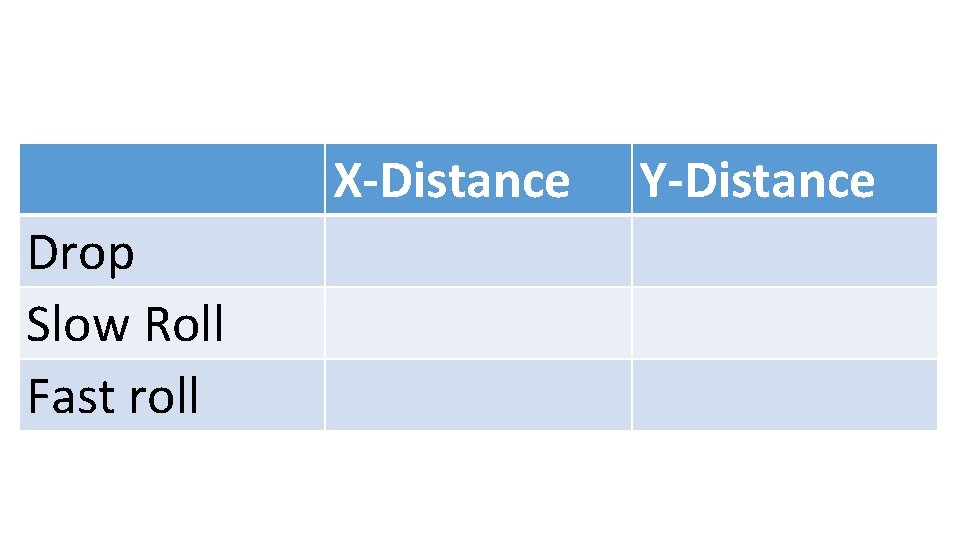
X-Distance Drop Slow Roll Fast roll Y-Distance

LAB Questions: 50 1) Draw (on page 51) the x-axis component and the y-axis component, and the actual path that the ball took in each trial. 2) What caused the x-axis component and how did it change with each trial? 3) What caused the y-axis component and how did it change with each trial? 4) Compare the line drawn from question 1 and the two components drawn during the experiment.

Projectile Motion Page 53

Essential Question: How does the moon maintain an orbit around the Earth?

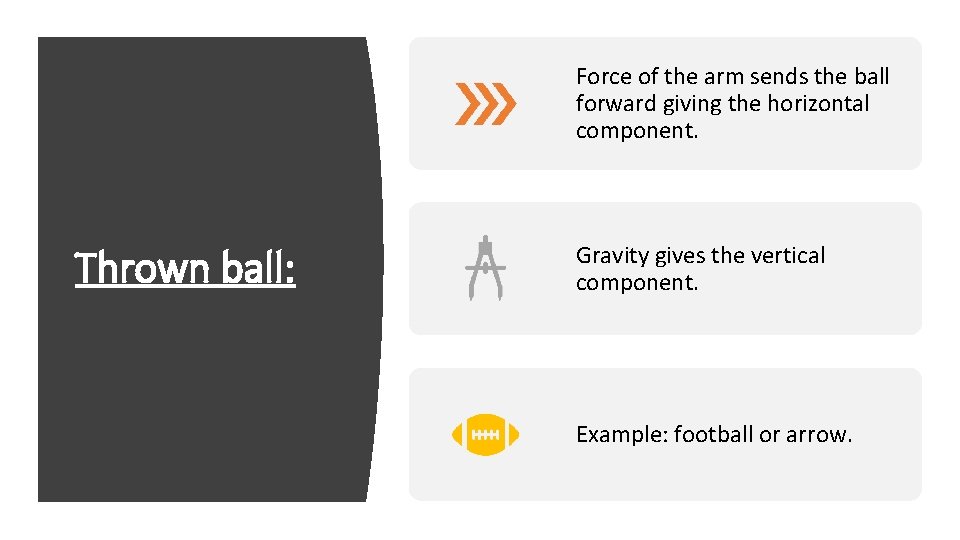
Projectile Motion: The curved path followed by an object that is thrown or launched near the Earth’s surface. Has a vertical component (up/down, y-axis) and a Horizontal component (sideways, x-axis). The combination of the 2 components results in a curved motion of the object. The 2 components are independent and do not affect each other.

Force of the arm sends the ball forward giving the horizontal component. Thrown ball: Gravity gives the vertical component. Example: football or arrow.

Is a type of projectile motion. Orbital motion. The object is moving away from the Earth, but is also falling toward the Earth. It fall toward the Earth at the same rate is moving away from the Earth, keeping at the same distance from the Earth’s surface.

For every action force, there is an equal and opposite reaction force. Forces always occur in pairs. (equal and opposite) Newton’s 3 rd Law. Force is present even if there is no motion. Equal force does not always have equal effects. Example: Soccer ball and Earth.

Name the 2 components of orbital motion, and explain why the objects stay in motion. Page 52: Projectile/3 rd Law Questions Give an example of Newton’s 3 rd law and explain how the law works in the example. A basketball player jumps to dunk a ball. What is the force pair? Why does the player accelerate? Why does it seem that the Earth does not accelerate?

Page 59 Force Math

Page 59: Force (F = ma) • What is the net force needed to accelerate a 1600 Kg car forward at 2. 0 m/s 2? • A baseball accelerates downward at a rate of 9. 8 m/s 2. If the gravitational force is 1. 4 N, what is the baseballs mass? • A sailboat and its crew have a combined mass 655 Kg. If a net force of 895 N is pushing the boat forward, what is the sailboats acceleration? • The net force forward on a model plane is 7. 0 N and the plane has a mass of 3. 2 Kg, what is the acceleration?

Page 58: Momentum (P = mv) Calculate the momentum of a 75 Kg skater moving forward at 16 m/s. If a baby on a train has a momentum of 25 Kg m/s, and a mass of 5. 0 Kg, what is its velocity? Calculate the velocity of a 0. 8 Kg kitten with a forward momentum of 5 kg m/s. What is the momentum of a 48. 5 Kg man standing still while waiting for a bus? Calculate the momentum of a 135 Kg ostrich running north at 16. 2 m/s.