Inequalities Recap Inequalities are Less Than Equal to

Inequalities Recap Inequalities are: < Less Than Equal to or Less Than > Greater Than Equal to or Greater Than

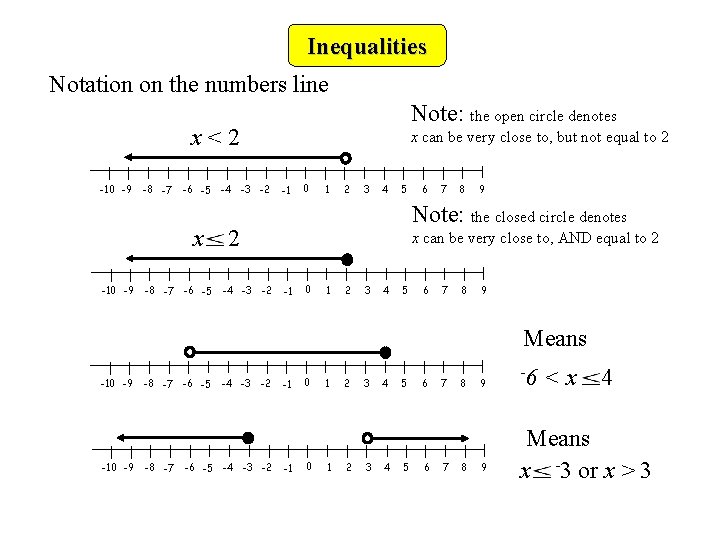
Inequalities Notation on the numbers line Note: the open circle denotes x<2 -10 -9 -8 -7 -6 -5 x -10 -9 -8 -7 -6 -5 -4 -3 -2 x can be very close to, but not equal to 2 -1 0 1 2 3 4 5 7 8 9 Note: the closed circle denotes 2 -4 -3 -2 6 x can be very close to, AND equal to 2 -1 0 1 2 3 4 5 6 7 8 9 Means -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 -1 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 -6 <x 4 Means x -3 or x > 3

Inequalities List the integer values for -3 < x -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 List the integer values for 7 1 -2, -1, 1 2 3 4 5 6 7 8 0, 1 9 x > -1 0, 1, 2, 3, 4, 5, 6, 7 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 List the integer values for 6 1 2 3 4 5 6 7 8 9 3 x > -4 3 2 x> -1, -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 0, 1, 2

Inequalities Now try these: List all the integer values that satisfy these inequalities: 1. -2 -2, -1, 0, 1, 2, 3 x 3 2. -4 < x < 0 -3, -2, -1 3. -8 4 n 15 -2, -1, 0, 1, 2, 3 4. -3 < 2 n 12 -1, 0, 1, 2, 3, 4, 5, 6 5. -5 2 n-1 < 6 -2, -1, 0, 1, 2, 3

Types of Data Discrete Data that can only have a specific value (often whole numbers) For example Number of people Shoe size Continuous Data You cannot have ½ or ¼ of a person. You might have a 6½ or a 7 but not a size 6. 23456 Data that can have any value within a range For example Time A person running a 100 m race could finish at any time between 10 seconds and 30 seconds with no restrictions Height As you grow from a baby to an adult you will at some point every height on the way

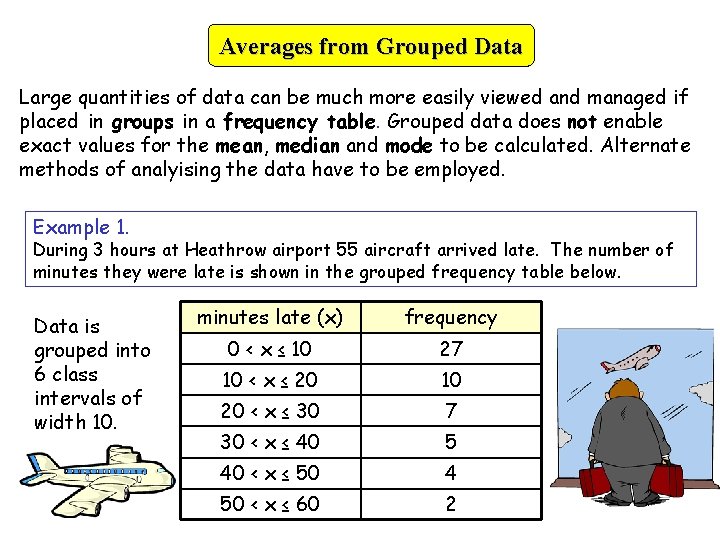
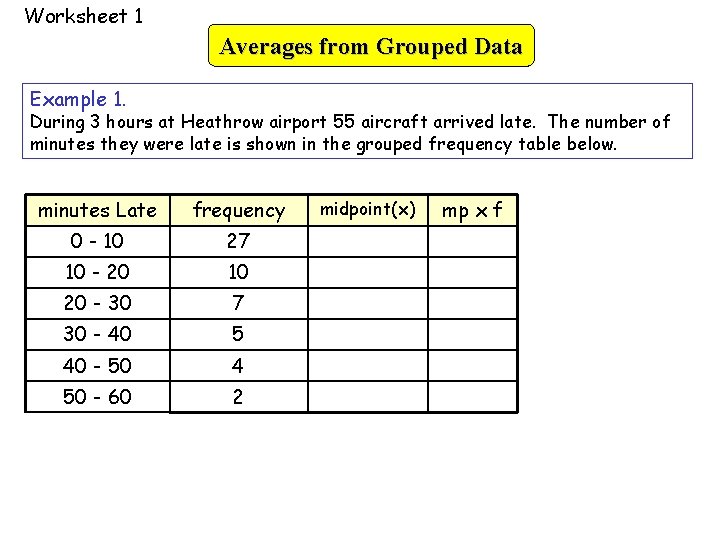
Averages from Grouped Data Large quantities of data can be much more easily viewed and managed if placed in groups in a frequency table. Grouped data does not enable exact values for the mean, median and mode to be calculated. Alternate methods of analyising the data have to be employed. Example 1. During 3 hours at Heathrow airport 55 aircraft arrived late. The number of minutes they were late is shown in the grouped frequency table below. Data is grouped into 6 class intervals of width 10. minutes late (x) frequency 0 < x ≤ 10 27 10 < x ≤ 20 10 20 < x ≤ 30 7 30 < x ≤ 40 5 40 < x ≤ 50 4 50 < x ≤ 60 2

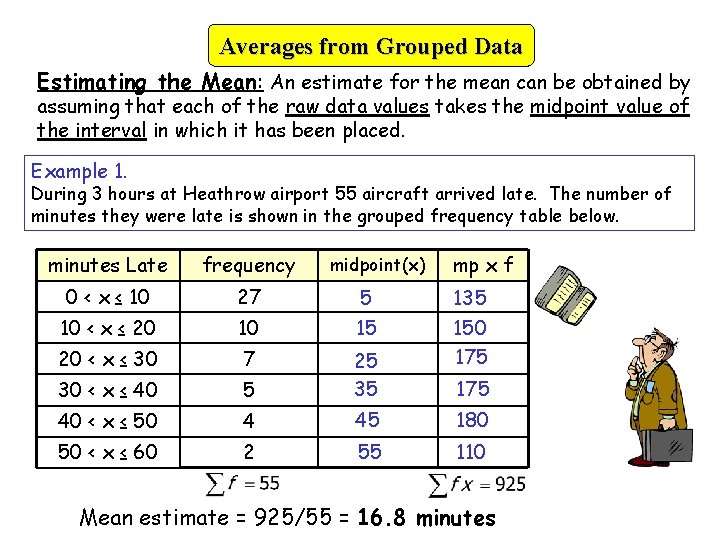
Averages from Grouped Data Estimating the Mean: An estimate for the mean can be obtained by assuming that each of the raw data values takes the midpoint value of the interval in which it has been placed. Example 1. During 3 hours at Heathrow airport 55 aircraft arrived late. The number of minutes they were late is shown in the grouped frequency table below. minutes Late frequency 0 < x ≤ 10 27 5 10 < x ≤ 20 10 15 20 < x ≤ 30 7 30 < x ≤ 40 5 25 35 40 < x ≤ 50 4 45 180 50 < x ≤ 60 2 55 110 midpoint(x) mp x f 135 150 175 Mean estimate = 925/55 = 16. 8 minutes

Averages from Grouped Data The Modal Class The modal class is simply the class interval of highest frequency. Example 1. During 3 hours at Heathrow airport 55 aircraft arrived late. The number of minutes they were late is shown in the grouped frequency table below. minutes late frequency 0 < x ≤ 10 27 10 < x ≤ 20 10 20 < x ≤ 30 7 30 < x ≤ 40 5 40 < x ≤ 50 4 50 < x ≤ 60 2 Modal class = 0 - 10

Averages from Grouped Data The Median Class Interval is the class interval containing the median. Example 1. During 3 hours at Heathrow airport 55 aircraft arrived late. The number of minutes they were late is shown in the grouped frequency table below. minutes late frequency 0 < x ≤ 10 27 10 < x ≤ 20 10 20 < x ≤ 30 7 30 < x ≤ 40 5 40 < x ≤ 50 4 50 < x ≤ 60 2 (55+1)/2 = 28 The 28 th data value is in the 10 - 20 class

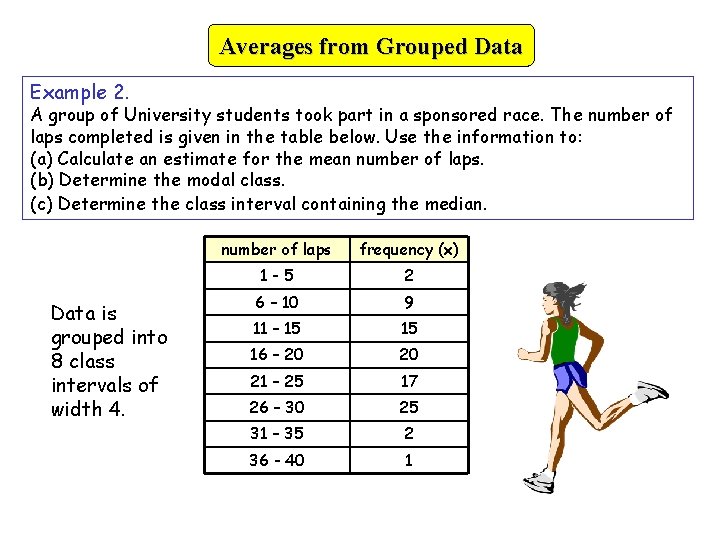
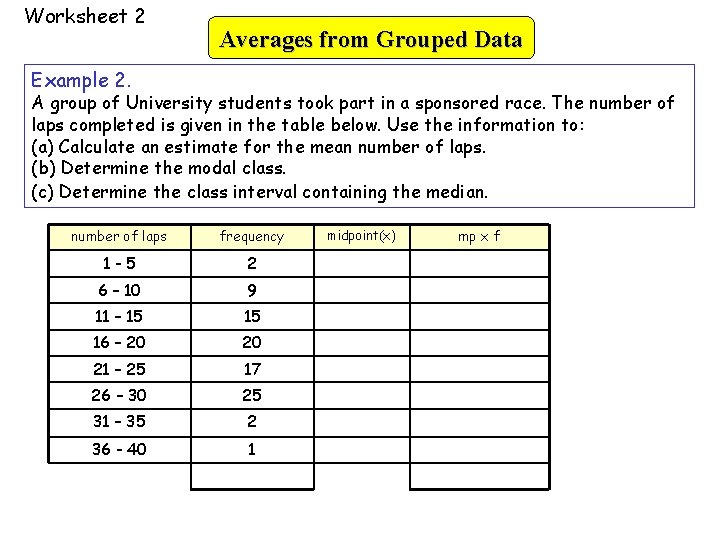
Averages from Grouped Data Example 2. A group of University students took part in a sponsored race. The number of laps completed is given in the table below. Use the information to: (a) Calculate an estimate for the mean number of laps. (b) Determine the modal class. (c) Determine the class interval containing the median. Data is grouped into 8 class intervals of width 4. number of laps frequency (x) 1 -5 2 6 – 10 9 11 – 15 15 16 – 20 20 21 – 25 17 26 – 30 25 31 – 35 2 36 - 40 1

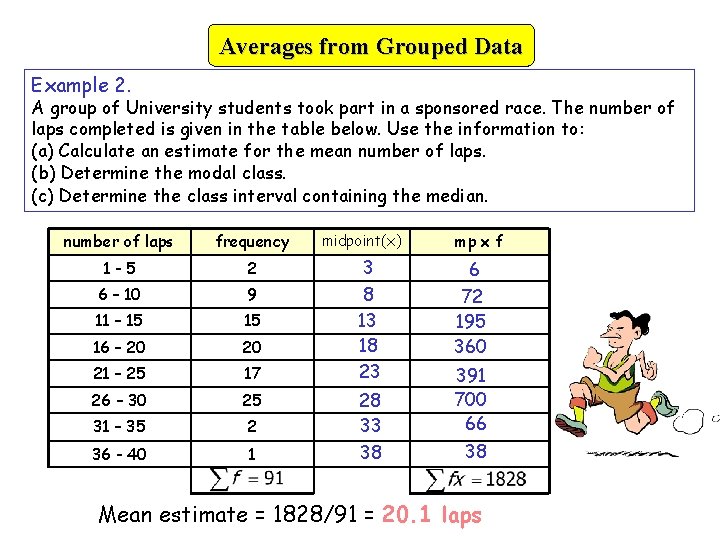
Averages from Grouped Data Example 2. A group of University students took part in a sponsored race. The number of laps completed is given in the table below. Use the information to: (a) Calculate an estimate for the mean number of laps. (b) Determine the modal class. (c) Determine the class interval containing the median. number of laps frequency 1 -5 2 6 – 10 9 11 – 15 15 16 – 20 20 21 – 25 17 26 – 30 25 31 – 35 2 36 - 40 1 midpoint(x) 3 8 13 18 23 28 33 38 mp x f 6 72 195 360 391 700 66 38 Mean estimate = 1828/91 = 20. 1 laps

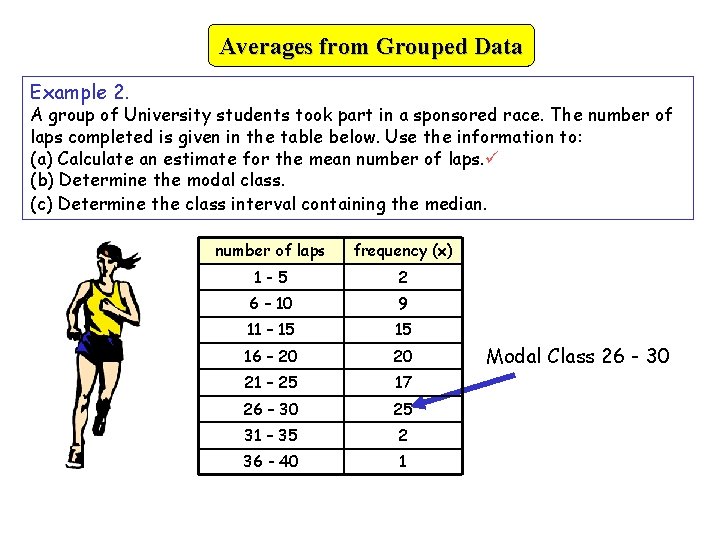
Averages from Grouped Data Example 2. A group of University students took part in a sponsored race. The number of laps completed is given in the table below. Use the information to: (a) Calculate an estimate for the mean number of laps. (b) Determine the modal class. (c) Determine the class interval containing the median. number of laps frequency (x) 1 -5 2 6 – 10 9 11 – 15 15 16 – 20 20 21 – 25 17 26 – 30 25 31 – 35 2 36 - 40 1 Modal Class 26 - 30

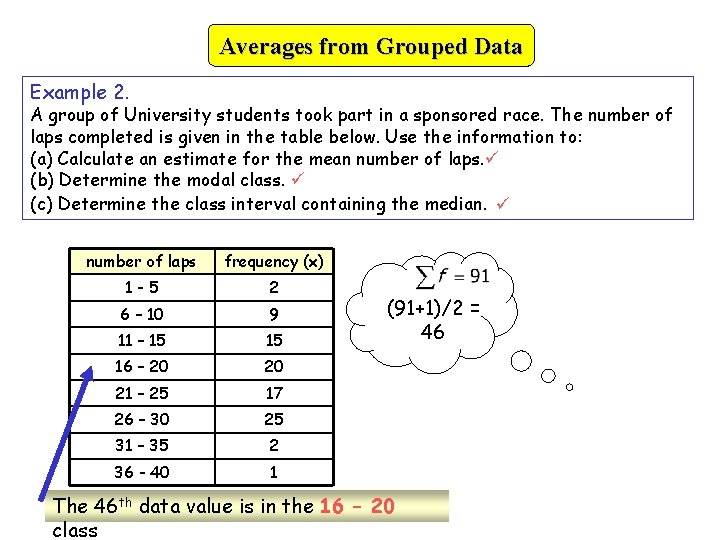
Averages from Grouped Data Example 2. A group of University students took part in a sponsored race. The number of laps completed is given in the table below. Use the information to: (a) Calculate an estimate for the mean number of laps. (b) Determine the modal class. (c) Determine the class interval containing the median. number of laps frequency (x) 1 -5 2 6 – 10 9 11 – 15 15 16 – 20 20 21 – 25 17 26 – 30 25 31 – 35 2 36 - 40 1 (91+1)/2 = 46 The 46 th data value is in the 16 – 20 class

Worksheet 1 Averages from Grouped Data Example 1. During 3 hours at Heathrow airport 55 aircraft arrived late. The number of minutes they were late is shown in the grouped frequency table below. minutes Late frequency 0 - 10 27 10 - 20 10 20 - 30 7 30 - 40 5 40 - 50 4 50 - 60 2 midpoint(x) mp x f

Worksheet 2 Averages from Grouped Data Example 2. A group of University students took part in a sponsored race. The number of laps completed is given in the table below. Use the information to: (a) Calculate an estimate for the mean number of laps. (b) Determine the modal class. (c) Determine the class interval containing the median. number of laps frequency 1 -5 2 6 – 10 9 11 – 15 15 16 – 20 20 21 – 25 17 26 – 30 25 31 – 35 2 36 - 40 1 midpoint(x) mp x f