INEQUALITIES Introduction An inequality is similar to an





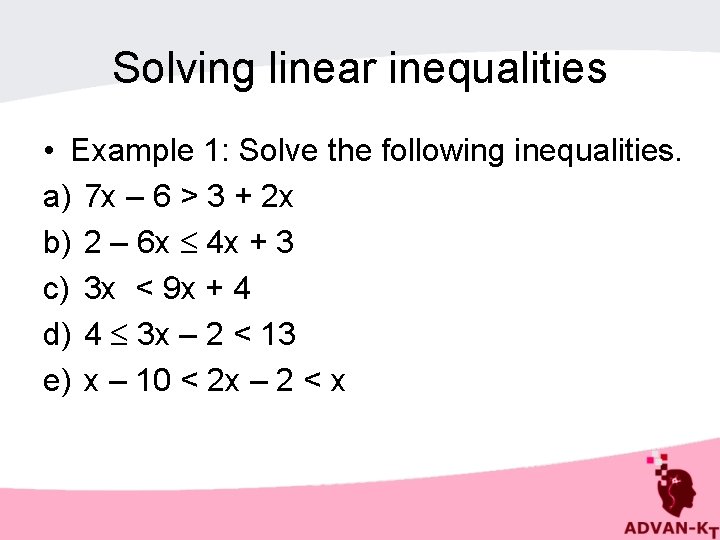





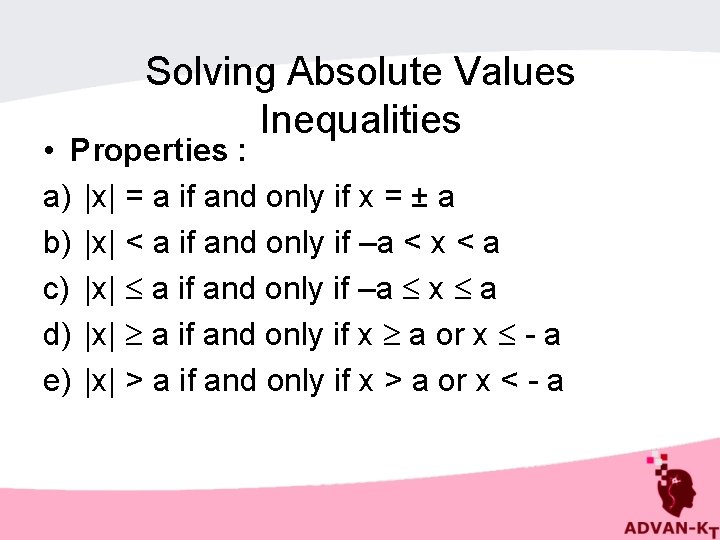
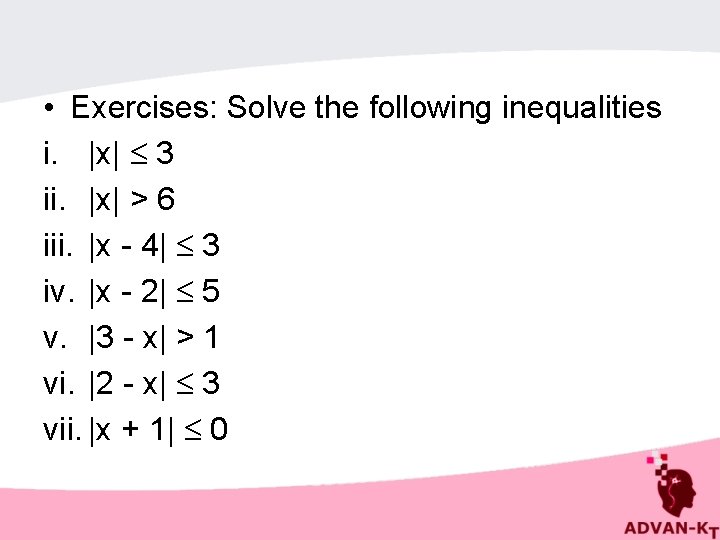
- Slides: 14

INEQUALITIES

Introduction • An inequality is similar to an equation except that the statement is that two expressions have a relationship other than equality, such as <, , > or .

Rules for inequalities • Rule 1: An equal quantity may be added to (or subtracted from) both sides of an inequality without changing the inequality • Example: Solve x – 3 > 5 • Solution: • x – 3 + 3 > 5 + 3 (add 3 to both sides) • Thus, the solution is x > 8

Rules for inequalities (cont) • Rule 2: An equal positive quantity may multiply (or divide) both sides of an inequality without changing the in equality • Example: Solve 2 x – 1 > 7 • Solution: 2 x – 1 + 1 > 7 + 1 (add 1 to both sides) • 2 x > 8 • (divide both sides by 2) • x > 4 (the inequality remain the same)

Rules for inequalities (cont) • Rule 3: If both sides of an inequality are multiplied (or divided) by a negative quantity then the inequality is reversed. • Example: Solve 3 – 2 x > -5 • Solution: 3 – 2 x > -5 – 3 (subtract 3 from both sides) • -2 x < -8 • (divide both sides by -2) • (Apply rule 3, the inequality
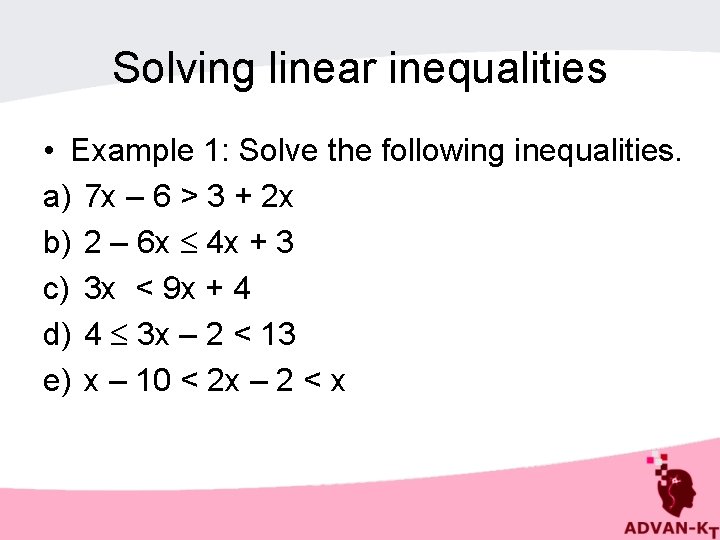
Solving linear inequalities • Example 1: Solve the following inequalities. a) 7 x – 6 > 3 + 2 x b) 2 – 6 x 4 x + 3 c) 3 x < 9 x + 4 d) 4 3 x – 2 < 13 e) x – 10 < 2 x – 2 < x

Solving Quadratic Inequalities • Quadratic inequalities need to handle with care. • Example 2: Solve x 2 – x – 12 > 0 • Step 1 : Factorize the quadratic expression (x + 3) (x – 4) > 0 Step 2: The critical points are: 4 and 3. + (x + 3) + Step 3 : Sketch a sign change diagram (x – 4) - + -3 - + 4 + The solution is x < -3 or x > 4

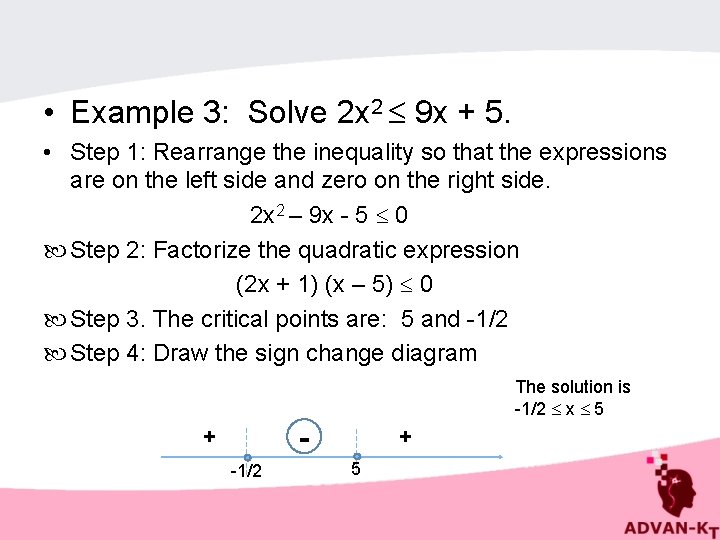
• Example 3: Solve 2 x 2 9 x + 5. • Step 1: Rearrange the inequality so that the expressions are on the left side and zero on the right side. 2 x 2 – 9 x - 5 0 Step 2: Factorize the quadratic expression (2 x + 1) (x – 5) 0 Step 3. The critical points are: 5 and -1/2 Step 4: Draw the sign change diagram The solution is -1/2 x 5 - + -1/2 + 5

• Example 4: Solve (2 – x)(x + 3) > 0 • Step 1: The critical points are: 2 and - 3 • Step 2: Make sure the coefficient of x is positive. (2 – x) = -x + 2 = -(x – 2) Note that the inequality is Hence (2 – x)(x + 3) >0 reversed -(x – 2)(x + 3) > 0 Multiple both sides with -1, -1 -(x – 2)(x + 3) < -1 0 (x – 2) (x + 3) < 0 Step 4: Draw a sign change diagram + -3 + 2 The solution is -3 < x < 2

Solving Absolute Values Inequalities • The absolute value of a real number x can be thought of as the distance from 0 to x |-x| |x| on a real number line. -x 0 x • |2| = 2 and |-2|= 2 • Absolute value, denoted as |x|, is defined as follows

Solving Absolute Values Inequalities • In a statement such as x < 2, it means that x must lie between 2 and -2. We can write this as |x|< 2 -2 < x < 2 Similarly, |x - 4|< 2 represents all points < 2 from point <2 whose distance 4 is less than 2. -x 4 x |x - 4|< 2 -2 < x – 4 < 2 2 < x < 6

Solving Absolute Values Inequalities • If |x| > 5, this means the distance from 0 to x is greater than 5. -x x -5 0 5 • This also indicates than the point x can be greater than 5 or less than -5. • |x| > 5 x > 5 or x < -5
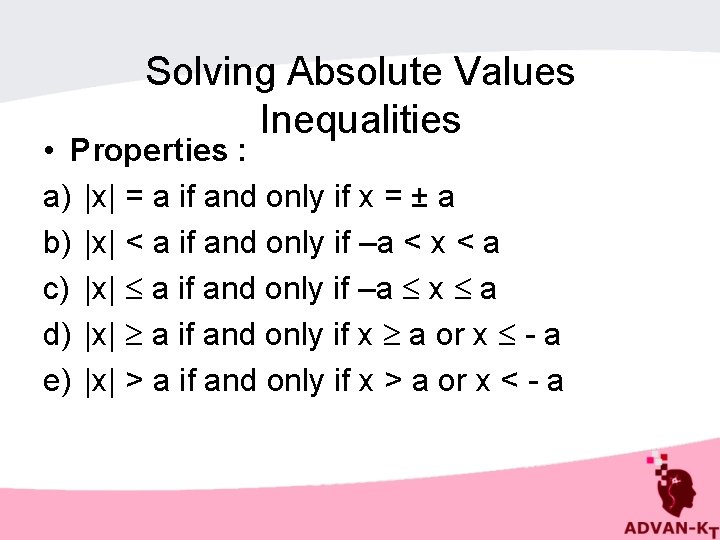
Solving Absolute Values Inequalities • Properties : a) |x| = a if and only if x = ± a b) |x| < a if and only if –a < x < a c) |x| a if and only if –a x a d) |x| a if and only if x a or x - a e) |x| > a if and only if x > a or x < - a
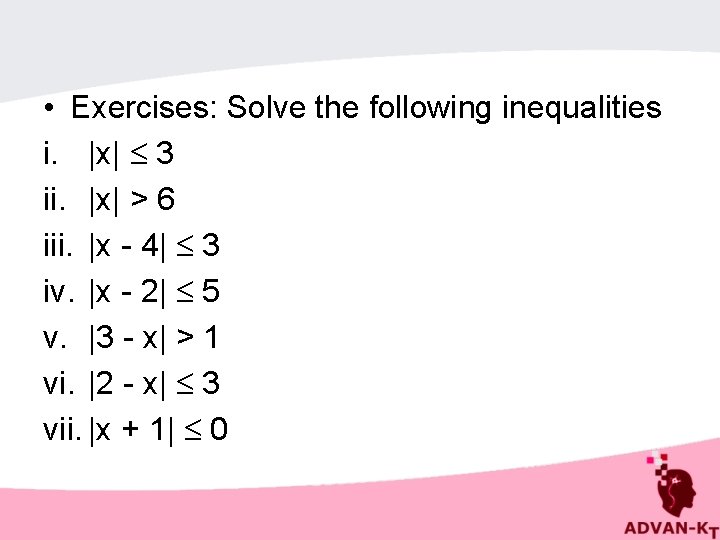
• Exercises: Solve the following inequalities i. |x| 3 ii. |x| > 6 iii. |x - 4| 3 iv. |x - 2| 5 v. |3 - x| > 1 vi. |2 - x| 3 vii. |x + 1| 0