Inequalities and Their Graphs Section 3 1 Part

Inequalities and Their Graphs Section 3 -1 Part 2

Goals Goal Rubric • To write and graph inequalities. Level 1 – Know the goals. Level 2 – Fully understand the goals. Level 3 – Use the goals to solve simple problems. Level 4 – Use the goals to solve more advanced problems. Level 5 – Adapts and applies the goals to different and more complex problems.

Vocabulary • None

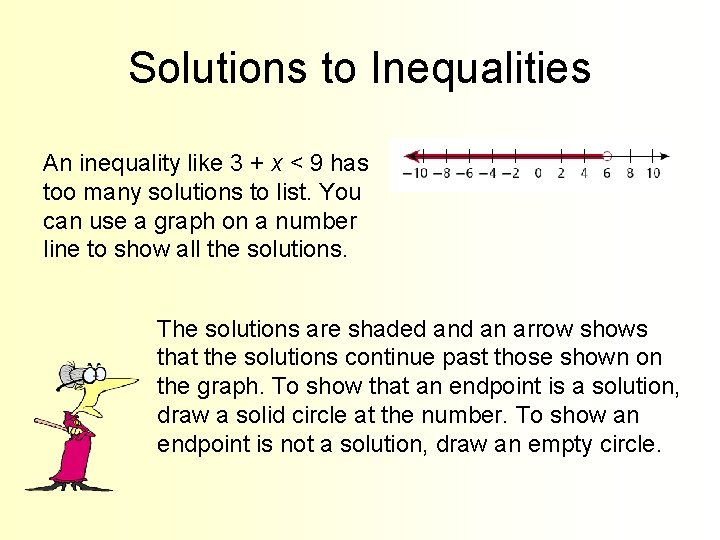
Solutions to Inequalities An inequality like 3 + x < 9 has too many solutions to list. You can use a graph on a number line to show all the solutions. The solutions are shaded an arrow shows that the solutions continue past those shown on the graph. To show that an endpoint is a solution, draw a solid circle at the number. To show an endpoint is not a solution, draw an empty circle.

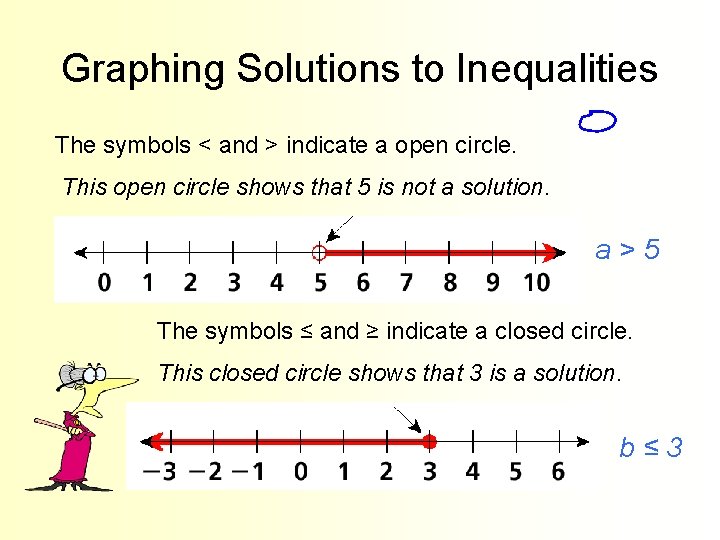
Graphing Solutions to Inequalities The symbols < and > indicate a open circle. This open circle shows that 5 is not a solution. a>5 The symbols ≤ and ≥ indicate a closed circle. This closed circle shows that 3 is a solution. b≤ 3

Graphing Solutions to Inequalities Always write the inequality with the variable on the left side, then the arrow points in the same direction as the inequality sign.

Rewriting Inequalities • When you rewrite an inequality to change which side the variable is on (reverse the inequality), you change the direct of the inequality sign (reverse the inequality sign) also. • Example: – If 4 < x, then x > 4 – If y ≥ -3, then -3 ≤ y

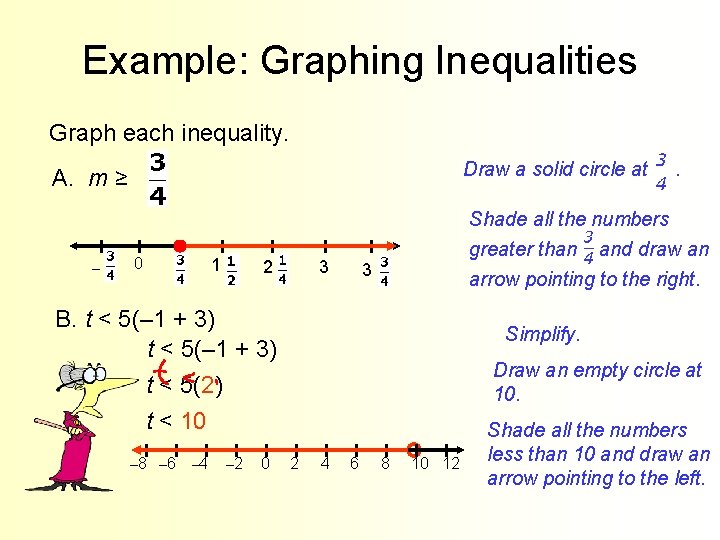
Example: Graphing Inequalities Graph each inequality. Draw a solid circle at A. m ≥ – 0 1 2 3 Shade all the numbers greater than and draw an arrow pointing to the right. 3 B. t < 5(– 1 + 3) Simplify. Draw an empty circle at 10. t < 5(2) t < 10 – 8 – 6 – 4 – 2 0 . 2 4 6 8 10 12 Shade all the numbers less than 10 and draw an arrow pointing to the left.

Graph each inequality. C. – 1 > y – 3 – 2 or y < - 1 – 1 0 1 2 3 Rewrite the inequality as y<-1. Draw an open circle at – 1. The solutions are all values of y less than – 1, so shade the line to the left of – 1.

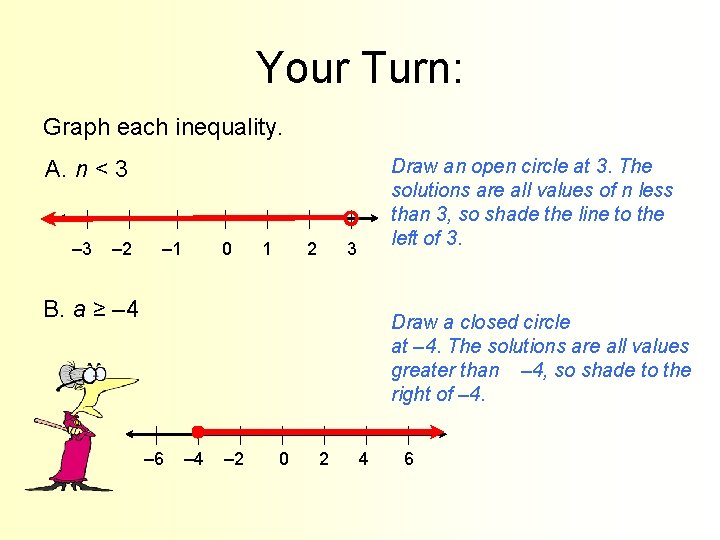
Your Turn: Graph each inequality. Draw an open circle at 3. The solutions are all values of n less than 3, so shade the line to the left of 3. A. n < 3 – 2 – 1 0 1 2 3 B. a ≥ – 4 Draw a closed circle at – 4. The solutions are all values greater than – 4, so shade to the right of – 4. – 6 – 4 – 2 0 2 4 6

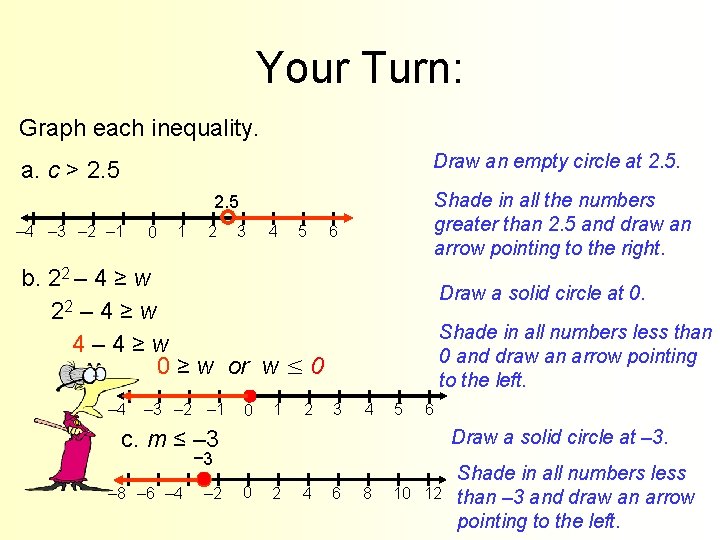
Your Turn: Graph each inequality. Draw an empty circle at 2. 5. a. c > 2. 5 Shade in all the numbers greater than 2. 5 and draw an arrow pointing to the right. 2. 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 6 b. 22 – 4 ≥ w 4– 4≥w 0 ≥ w or w ≤ 0 – 4 – 3 – 2 – 1 0 1 2 Draw a solid circle at 0. Shade in all numbers less than 0 and draw an arrow pointing to the left. 3 4 5 6 c. m ≤ – 3 Draw a solid circle at – 3. − 3 – 8 – 6 – 4 – 2 0 2 4 6 8 10 12 Shade in all numbers less than – 3 and draw an arrow pointing to the left.

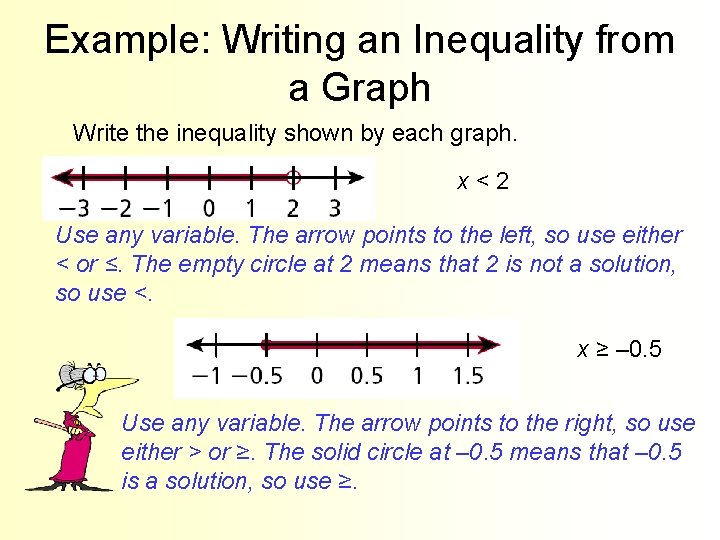
Example: Writing an Inequality from a Graph Write the inequality shown by each graph. x<2 Use any variable. The arrow points to the left, so use either < or ≤. The empty circle at 2 means that 2 is not a solution, so use <. x ≥ – 0. 5 Use any variable. The arrow points to the right, so use either > or ≥. The solid circle at – 0. 5 means that – 0. 5 is a solution, so use ≥.

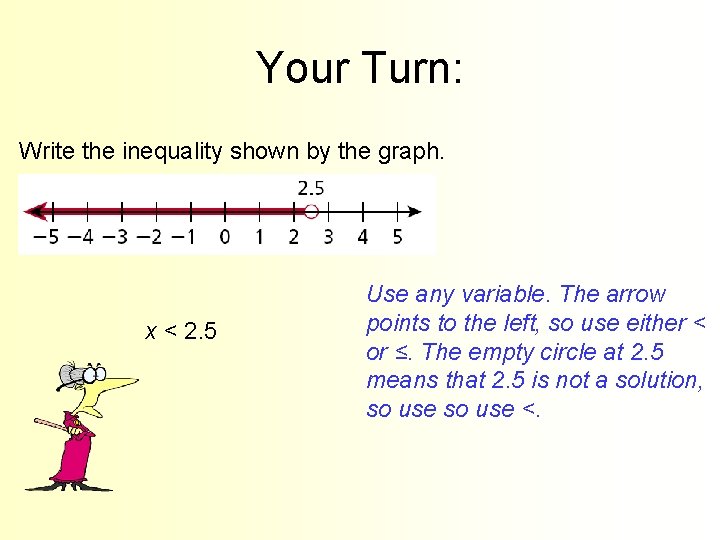
Your Turn: Write the inequality shown by the graph. x < 2. 5 Use any variable. The arrow points to the left, so use either < or ≤. The empty circle at 2. 5 means that 2. 5 is not a solution, so use <.

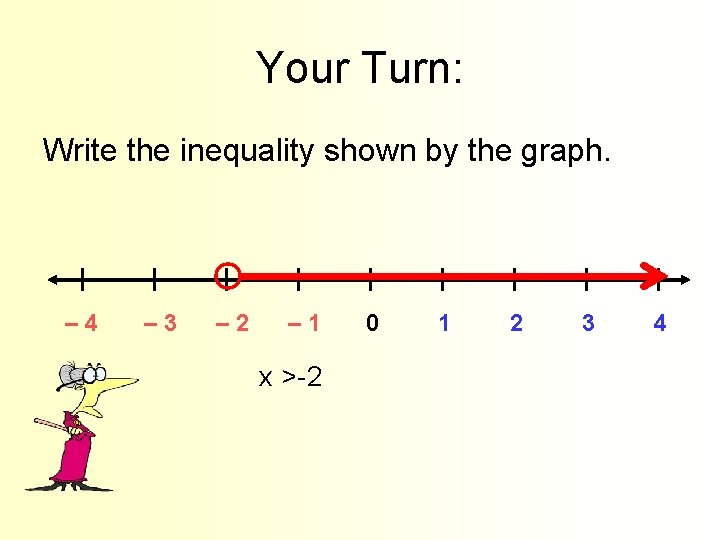
Your Turn: Write the inequality shown by the graph. | | | | | – 4 – 3 – 2 – 1 0 1 2 3 4 x >-2

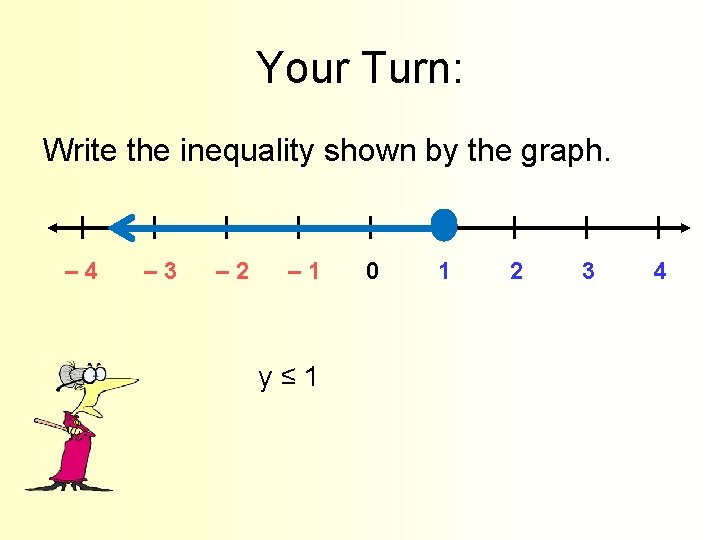
Your Turn: Write the inequality shown by the graph. | | | | | – 4 – 3 – 2 – 1 0 1 2 3 4 y≤ 1

Reading Math “No more than” means “less than or equal to. ” “At least” means “greater than or equal to”.

Example: Application Ray’s dad told him not to turn on the air conditioner unless the temperature is at least 85°F. Define a variable and write an inequality for the temperatures at which Ray can turn on the air conditioner. Graph the solutions. Let t represent the temperatures at which Ray can turn on the air conditioner. Turn on the AC when temperature t ≥ t 85 70 75 80 is at least 85 90 85°F 85 Draw a solid circle at 85. Shade all numbers greater than 85 and draw an arrow pointing to the right.

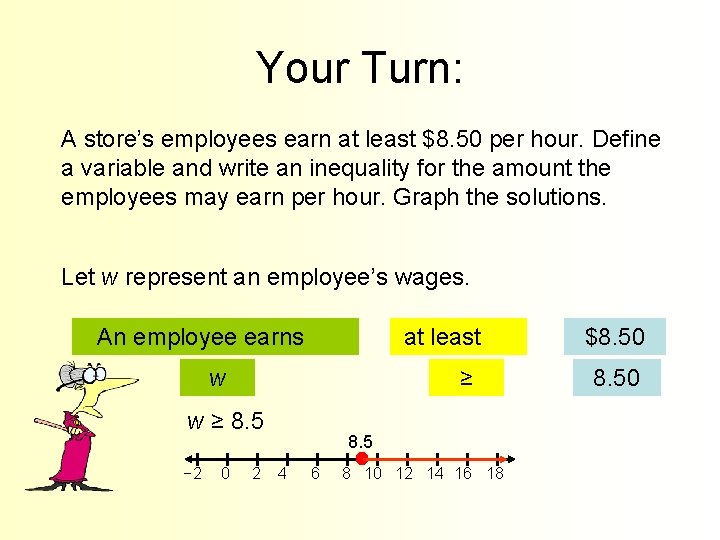
Your Turn: A store’s employees earn at least $8. 50 per hour. Define a variable and write an inequality for the amount the employees may earn per hour. Graph the solutions. Let w represent an employee’s wages. An employee earns at least w ≥ 8. 5 − 2 0 2 8. 5 4 6 8 10 12 14 16 18 $8. 50

Joke Time • What has 18 legs and catches flies? • A baseball team. • Who stole the soap? • The robber ducky! • What happened to the plant on the windowsill of the classroom? • It grew square roots!

Assignment 3. 1 pt 2 Exercises Pg. 181 #5 -26