Inductive Representation Learning on Large Graphs William L

Inductive Representation Learning on Large Graphs William L. Hamilton, Rex Ying, Jure Leskovec Keshav Balasubramanian

Outline �Main goal: generating node embeddings �Survey of past methods �GCNs �Graph. SAGE �Algorithm �Optimization and learning �Aggregators �Experiments and results �Conclusion

Node Embeddings �Fixed length vector representations of nodes in a graph (similar to word embeddings) �Can be used in downstream machine learning and graph mining tasks �Need to learn smaller dense embeddings from higher dimensional information

Methods �Non Deep Learning based models: Deep. Walk, node 2 vec �Biased random walk based approaches �Attempt to linearize a graph by viewing the results of the walks as sentences � Deep Learning models: Vanilla graph neural networks, GCNs �Neural Networks learn the representations

Graph Convolution Networks �Type of deep learning model that learns node representations �Two approaches: �Spectral – Involves operating in the spectral domain of the graph, specifically on the Laplacian and Adjacency matrix. �Spatial – Convolution is defined directly based on the spatial neighborhood of a node �Drawbacks of the spectral approach �Involves operating on entire Laplacian �Transductive, generalizes poorly to unseen nodes

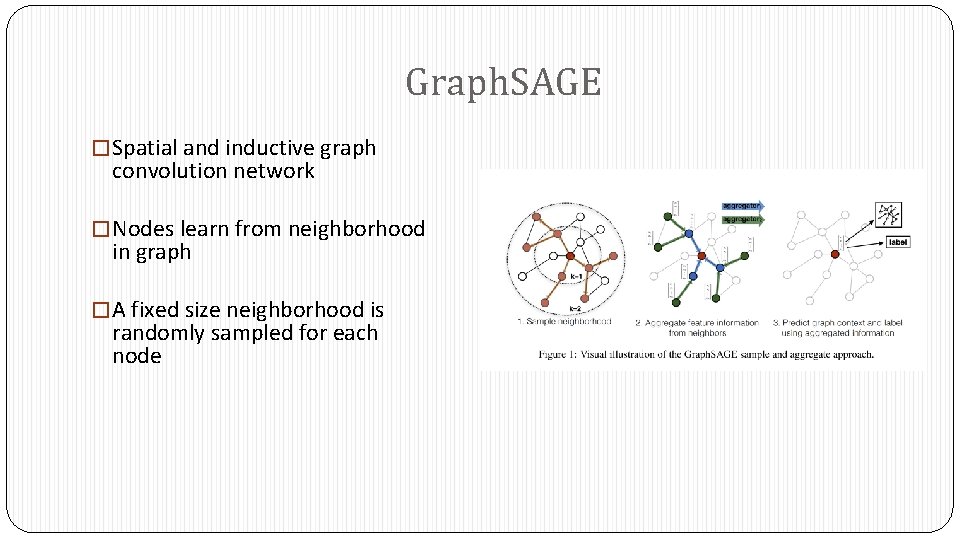
Graph. SAGE � Spatial and inductive graph convolution network � Nodes learn from neighborhood in graph � A fixed size neighborhood is randomly sampled for each node

Algorithm �Graph. SAGE forward pass

Learning the parameters of the network �Supervised �Final embeddings are passed through a dense layer to get class probabilities �Eg: Labelling the nodes of a graph �End goal is labelling the node, not generating the embedding � Unsupervised �Use custom loss function that ensure “nearby” nodes have similar representations, “far away” nodes have dissimilar representations �Negative sample to ensure latter �Nearness defined by cooccurrence score on a fixed length random walk

Aggregators �Mean: �Pooling: �LSTM based aggregator

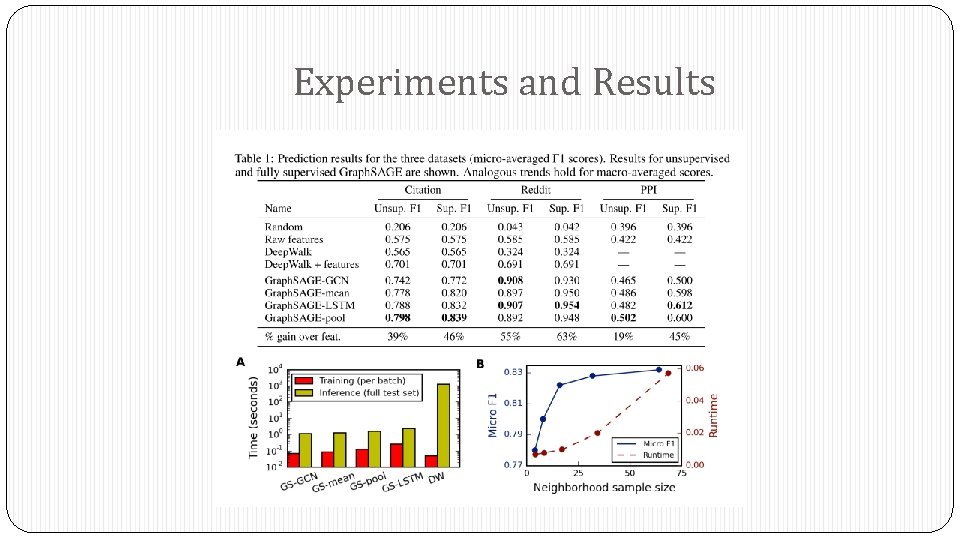
Experiments and Results

Conclusion �Proposed an inductive framework to learn node representations based on spatial graph convolutions