Inductive Learning 12 Decision Tree Method Russell and

Inductive Learning (1/2) Decision Tree Method Russell and Norvig: Chapter 18, Sections 18. 1 through 18. 4 Chapter 18, Sections 18. 1 through 18. 3 CS 121 – Winter 2003

Quotes “Our experience of the world is specific, yet we are able to formulate general theories that account for the past and predict the future” Genesereth and Nilsson, Logical Foundations of AI, 1987 “Entities are not to be multiplied without necessity” Ockham, 1285 -1349

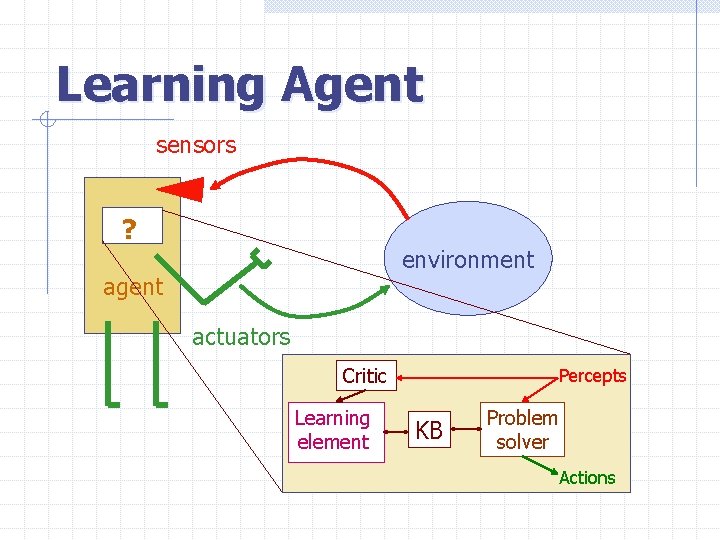
Learning Agent sensors ? environment agent actuators Critic Learning element Percepts KB Problem solver Actions

Contents Introduction to inductive learning Logic-based inductive learning: n n Decision tree method Version space method Function-based inductive learning n Neural nets

Contents Introduction to inductive learning Logic-based inductive learning: n n Decision tree method Version space method 2 + why inductive learning works Function-based inductive learning n 1 Neural nets 3

Inductive Learning Frameworks 1. Function-learning formulation 2. Logic-inference formulation

Function-Learning Formulation Goal function f Training set: (xi, f(xi)), i = 1, …, n Inductive inference: Find a function h that fits the point well f(x) x Neural nets

Logic-Inference Formulation Background knowledge KB Training set D (observed knowledge) such that KB D and {KB, D} is satisfiable Inductive inference: Find h (inductive hypothesis) such that n {KB, h} is satisfiable h = D is a trivial, n KB, h D but uninteresting solution (data caching) Usually, not a sound inference

Rewarded Card Example Deck of cards, with each card designated by [r, s], its rank and suit, and some cards “rewarded” Background knowledge KB: ((r=1) v … v (r=10)) NUM(r) ((r=J) v (r=Q) v (r=K)) FACE(r) ((s=S) v (s=C)) BLACK(s) ((s=D) v (s=H)) RED(s) Training set D: REWARD([4, C]) REWARD([7, C]) REWARD([2, S]) REWARD([5, H]) REWARD([J, S])

Rewarded Card Example Background knowledge KB: ((r=1) v … v (r=10)) NUM(r) ((r=J) v (r=Q) v (r=K)) FACE(r) ((s=S) v (s=C)) BLACK(s) There are several possible ((s=D) v (s=H)) RED(s) inductive hypotheses Training set D: REWARD([4, C]) REWARD([7, C]) REWARD([2, S]) REWARD([5, H]) REWARD([J, S]) Possible inductive hypothesis: h (NUM(r) BLACK(s) REWARD([r, s]))

Learning a Predicate Set E of objects (e. g. , cards) Goal predicate CONCEPT(x), where x is an object in E, that takes the value True or False (e. g. , REWARD) Example: CONCEPT describes the precondition of an action, e. g. , Unstack(C, A) • E is the set of states • CONCEPT(x) HANDEMPTY x, BLOCK(C) x, BLOCK(A) x, CLEAR(C) x, ON(C, A) x Learning CONCEPT is a step toward learning the action

Learning a Predicate Set E of objects (e. g. , cards) Goal predicate CONCEPT(x), where x is an object in E, that takes the value True or False (e. g. , REWARD) Observable predicates A(x), B(X), … (e. g. , NUM, RED) Training set: values of CONCEPT for some combinations of values of the observable predicates

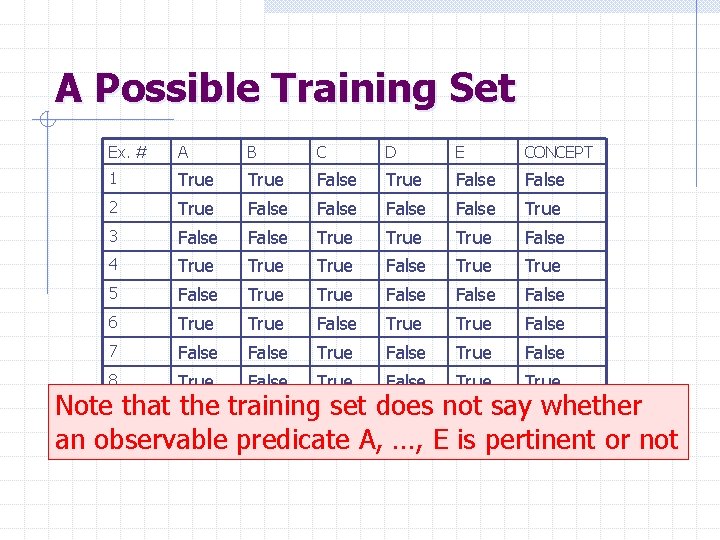
A Possible Training Set Ex. # A B C D E CONCEPT 1 True False 2 True False True 3 False True False 4 True False True 5 False True False 6 True False 7 False True False 8 True False True Note 9 that False the training set does whether False True not Truesay. False 10 True predicate True A, True an observable …, E False is pertinent or not

Learning a Predicate Set E of objects (e. g. , cards) Goal predicate CONCEPT(x), where x is an object in E, that takes the value True or False (e. g. , REWARD) Observable predicates A(x), B(X), … (e. g. , NUM, RED) Training set: values of CONCEPT for some combinations of values of the observable predicates Find a representation of CONCEPT in the form: CONCEPT(x) S(A, B, …) where S(A, B, …) is a sentence built with the observable predicates, e. g. : CONCEPT(x) A(x) ( B(x) v C(x))

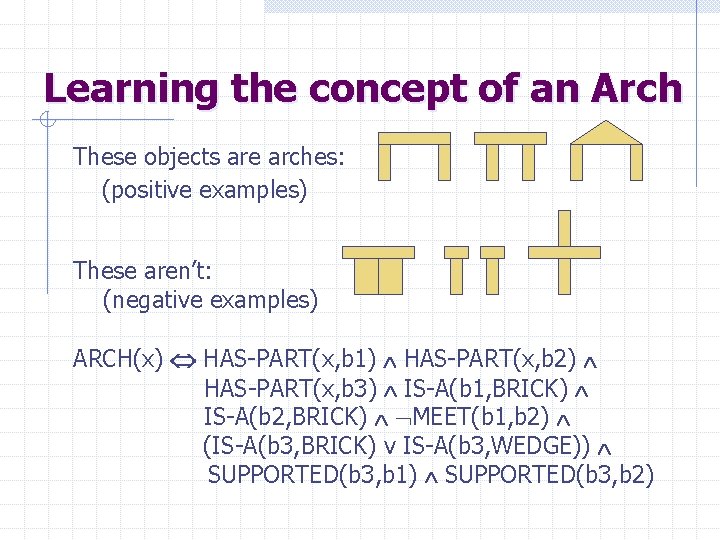
Learning the concept of an Arch These objects are arches: (positive examples) These aren’t: (negative examples) ARCH(x) HAS-PART(x, b 1) HAS-PART(x, b 2) HAS-PART(x, b 3) IS-A(b 1, BRICK) IS-A(b 2, BRICK) MEET(b 1, b 2) (IS-A(b 3, BRICK) v IS-A(b 3, WEDGE)) SUPPORTED(b 3, b 1) SUPPORTED(b 3, b 2)

Example set An example consists of the values of CONCEPT and the observable predicates for some object x A example is positive if CONCEPT is True, else it is negative The set E of all examples is the example set The training set is a subset of E a small one!

Hypothesis Space An hypothesis is any sentence h of the form: CONCEPT(x) S(A, B, …) where S(A, B, …) is a sentence built with the observable predicates The set of all hypotheses is called the hypothesis space H An hypothesis h agrees with an example if it gives the correct value of CONCEPT It is called a space because it has some internal structure

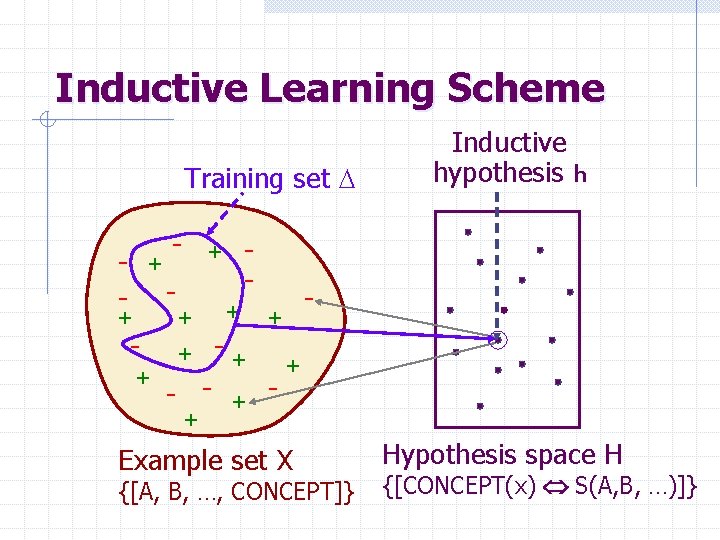
Inductive Learning Scheme Training set D - + + + - + - Inductive hypothesis h + Example set X {[A, B, …, CONCEPT]} Hypothesis space H {[CONCEPT(x) S(A, B, …)]}

Size of Hypothesis Space n observable predicates 2 n entries in truth table In the absence of any restriction (bias), 2 n there are 2 hypotheses to choose from n = 6 2 x 1019 hypotheses!

Multiple Inductive Hypotheses Need for a system of preferences – called a bias – to compare possible hypotheses h 1 NUM(x) BLACK(x) REWARD(x) h 2 BLACK([r, s]) (r=J) REWARD([r, s]) h 3 ([r, s]=[4, C]) ([r, s]=[7, C]) [r, s]=[2, S]) REWARD([r, s]) h 3 ([r, s]=[5, H]) ([r, s]=[J, S]) REWARD([r, s]) agree with all the examples in the training set

Keep-It-Simple (KIS) Bias Motivation If an hypothesis is too complex it may not be worth learning If the bias allows only sentences S that are it (data caching might just do the job as well) conjunctions offewer k << n predicates picked from n There are much simple hypotheses than complex ones, the hypothesis space is smaller thehence n observable predicates, then the size of n HExamples: is O(nk) n n Use much fewer observable predicates than suggested by the training set Constrain the learnt predicate, e. g. , to use only “high-level” observable predicates such as NUM, FACE, BLACK, and RED and/or to have simple syntax (e. g. , conjunction of literals)

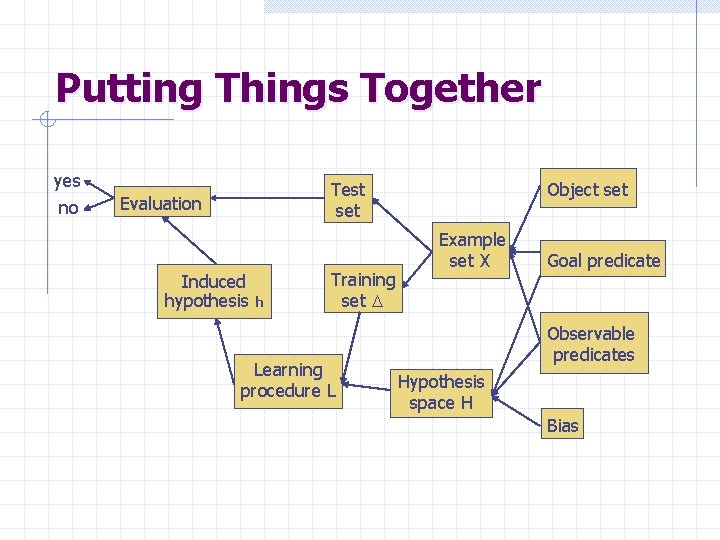
Putting Things Together yes no Test set Evaluation Induced hypothesis h Training set D Learning procedure L Object set Example set X Goal predicate Observable predicates Hypothesis space H Bias

Predicate-Learning Methods Decision tree Version space

Predicate as a Decision Tree The predicate CONCEPT(x) A(x) ( B(x) v C(x)) can be represented by the following decision tree: Example: A? A mushroom is poisonous iff True it is yellow and small, or yellow, big and spotted B? • x is a mushroom False True • CONCEPT = POISONOUS • A = YELLOW True • B = BIG C? • C = SPOTTED True False

Predicate as a Decision Tree The predicate CONCEPT(x) A(x) ( B(x) v C(x)) can be represented by the following decision tree: Example: A? A mushroom is poisonous iff True it is yellow and small, or yellow, big and spotted B? • x is a mushroom False True • CONCEPT = POISONOUS • A = YELLOW True • B = BIG C? • C = SPOTTED True False • D = FUNNEL-CAP • E = BULKY True False

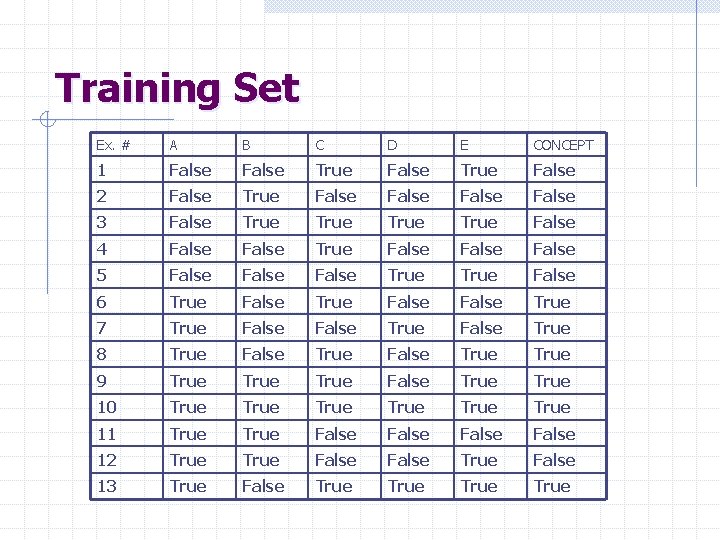
Training Set Ex. # A B C D E CONCEPT 1 False True False 2 False True False 3 False True False 4 False True False 5 False True False 6 True False True 7 True False True 8 True False True 9 True False True 10 True True 11 True False 12 True False 13 True False True

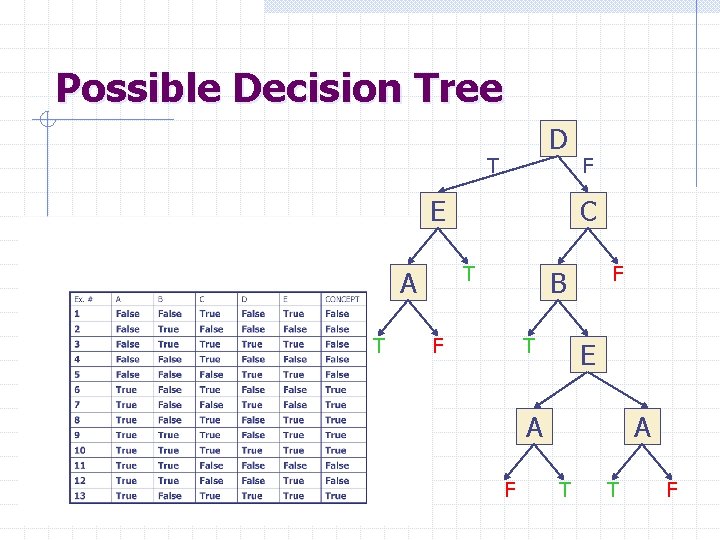
Possible Decision Tree D T E T C T A F F B F T E A A F T T F

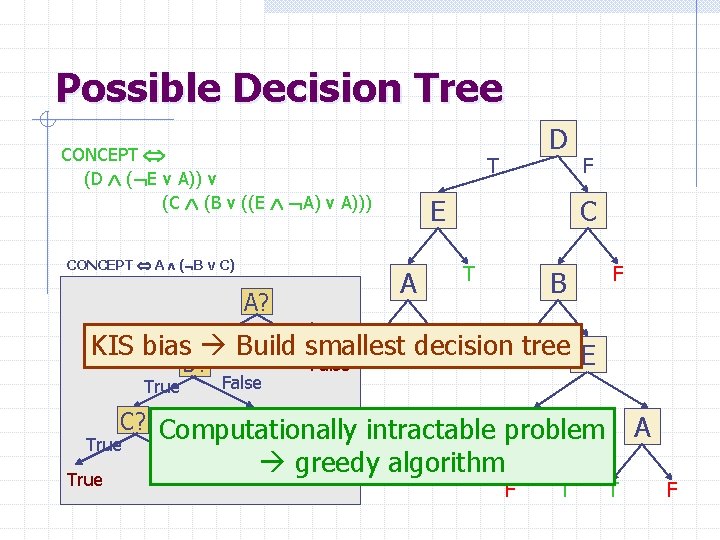
Possible Decision Tree CONCEPT (D ( E v A)) v (C (B v ((E A) v A))) CONCEPT A ( B v C) True T E A A? D F C T B F False T decision F T KIS bias Build smallest tree E False B? True False True C? Computationally A intractable problem False True False greedy algorithm F T A T F

Getting Started The distribution of the training set is: True: 6, 7, 8, 9, 10, 13 False: 1, 2, 3, 4, 5, 11, 12 Ex. # A B C D E CONCEPT 1 False True False 2 False True False 3 False True False 4 False True False 5 False True False 6 True False True 7 True False True 8 True False True 9 True False True 10 True True 11 True False 12 True False 13 True False True

Getting Started The distribution of training set is: True: 6, 7, 8, 9, 10, 13 False: 1, 2, 3, 4, 5, 11, 12 Without testing any observable predicate, we could report that CONCEPT is False (majority rule) with an estimated probability of error P(E) = 6/13

Getting Started The distribution of training set is: True: 6, 7, 8, 9, 10, 13 False: 1, 2, 3, 4, 5, 11, 12 Without testing any observable predicate, we could report that CONCEPT is False (majority rule) with an estimated probability of error P(E) = 6/13 Assuming that we will only include one observable predicate in the decision tree, which predicate should we test to minimize the probability or error?

Assume It’s A A T True: False: 6, 7, 8, 9, 10, 13 11, 12 F 1, 2, 3, 4, 5 If we test only A, we will report that CONCEPT is True if A is True (majority rule) and False otherwise The estimated probability of error is: Pr(E) = (8/13)x(2/8) + (5/8)x 0 = 2/13

Assume It’s B B T True: False: 9, 10 2, 3, 11, 12 F 6, 7, 8, 13 1, 4, 5 If we test only B, we will report that CONCEPT is False if B is True and True otherwise The estimated probability of error is: Pr(E) = (6/13)x(2/6) + (7/13)x(3/7) = 5/13

Assume It’s C C T True: False: 6, 8, 9, 10, 13 1, 3, 4 F 7 1, 5, 11, 12 If we test only C, we will report that CONCEPT is True if C is True and False otherwise The estimated probability of error is: Pr(E) = (8/13)x(3/8) + (5/13)x(1/5) = 4/13

Assume It’s D D T True: False: 7, 10, 13 3, 5 F 6, 8, 9 1, 2, 4, 11, 12 If we test only D, we will report that CONCEPT is True if D is True and False otherwise The estimated probability of error is: Pr(E) = (5/13)x(2/5) + (8/13)x(3/8) = 5/13

Assume It’s E E T True: False: 8, 9, 10, 13 1, 3, 5, 12 F 6, 7 2, 4, 11 to testis False, is A If we. So, test the only Ebest we willpredicate report that CONCEPT independent of the outcome The estimated probability of error is unchanged: Pr(E) = (8/13)x(4/8) + (5/13)x(2/5) = 6/13

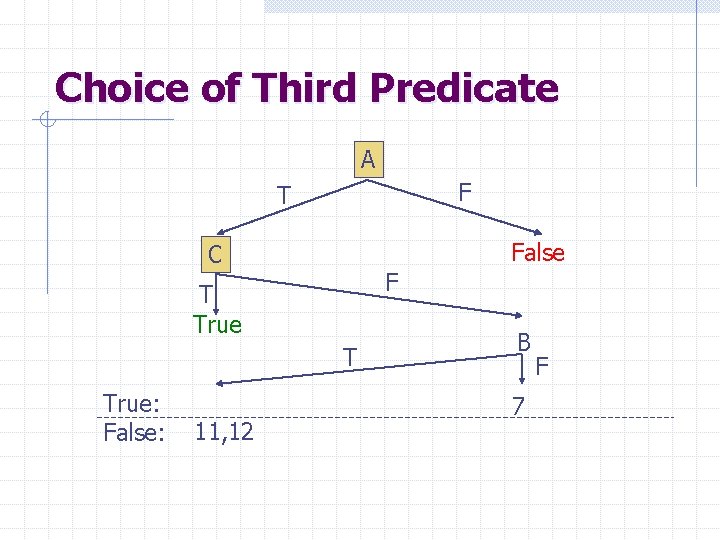
Choice of Second Predicate A F T C T True: False: 6, 8, 9, 10, 13 False F 7 11, 12 The majority rule gives the probability of error Pr(E|A) = 1/8 and Pr(E) = 1/13

Choice of Third Predicate A F T False C F T True: False: 11, 12 B 7 F

Final Tree True A True C C? B? A? False False True False True B True False True L CONCEPT A (C v B)

Learning a Decision Tree DTL(D, Predicates) 1. If all examples in D are positive then return True 2. If all examples in D are negative then return False 3. If Predicates is empty then return failure 4. A most discriminating predicate in Predicates 5. Return the tree whose: - root is A, - left branch is DTL(D+A, Predicates-A), branch Noise -inright training set!is DTL(D-A, Predicates-A) May return majority rule, Subset of examples instead of failure that satisfy A

Using Information Theory Rather than minimizing the probability of error, most existing learning procedures try to minimize the expected number of questions needed to decide if an object x satisfies CONCEPT This minimization is based on a measure of the “quantity of information” that is contained in the truth value of an observable predicate

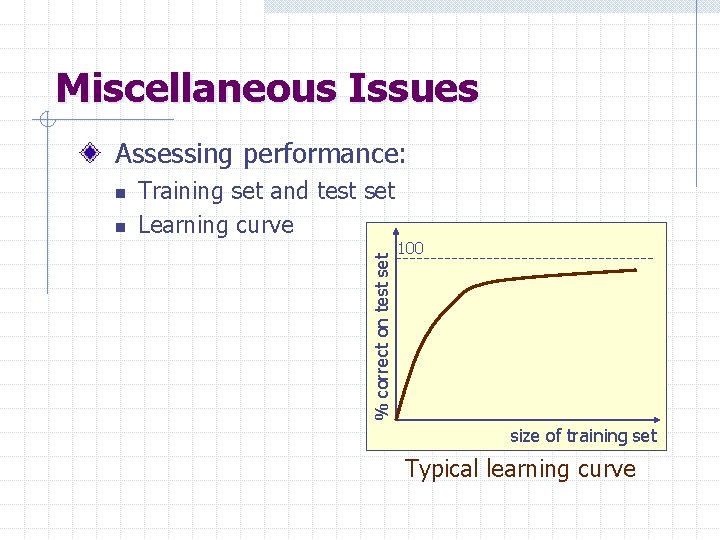
Miscellaneous Issues Assessing performance: n Training set and test set Learning curve % correct on test set n 100 size of training set Typical learning curve

Miscellaneous Issues Assessing performance: n n Training set and test set Learning curve Overfitting n Tree pruning Risk of using irrelevant observable predicates The resulting decision tree + to hypothesis majoritygenerate rule mayan not classify that all agrees with all correctly examples in examples the training setin the training set Terminate recursion when information gain is too small

Miscellaneous Issues The value of an observable Assessing performance: predicate P is unknown for n Training set and test set an example x. Then construct n Learning curve a decision tree for both values Overfitting of P and select the value that n Tree pruning ends up classifying x in the n Cross-validation largest class Missing data

Miscellaneous Issues Assessing performance: n n Training set and test set Learning curve n Select threshold that maximizes information gain Tree pruning n Cross-validation Overfitting Missing data Multi-valued and continuous attributes These issues occur with virtually any learning method

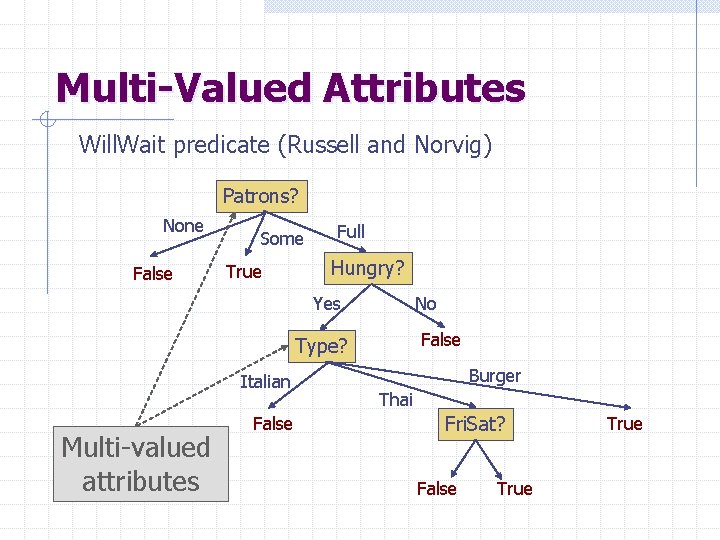
Multi-Valued Attributes Will. Wait predicate (Russell and Norvig) Patrons? None False Some True Full Hungry? Yes No False Type? Italian Multi-valued attributes False Burger Thai Fri. Sat? False True

Applications of Decision Tree Medical diagnostic / Drug design Evaluation of geological systems for assessing gas and oil basins Early detection of problems (e. g. , jamming) during oil drilling operations Automatic generation of rules in expert systems

Summary Inductive learning frameworks Logic inference formulation Hypothesis space and KIS bias Inductive learning of decision trees Assessing performance Overfitting