Inductive Argument Forms 2018 Taylor Francis Induction vs

Inductive Argument Forms © 2018 Taylor & Francis

Induction vs. deduction • Inductive arguments aim to make the conclusion probable, not certain, though sometimes, extremely probable. • False conclusion is logically compatible with true premises. • A strong inductive argument: one where true premises would render the conclusion highly likely. • inductive counterpart of validity © 2018 Taylor & Francis

Induction vs. deduction • Strength of inductive argument comes in degrees. • Additional information can make it rational to retract the conclusion, without retracting the premises. © 2018 Taylor & Francis

Statistical Syllogism © 2018 Taylor & Francis

Most • All As are Bs • x is an A • x is a B universal statistical modus syllogism ponens Still a reasonable inference, but no longer deductive, no longer UMP © 2018 Taylor & Francis

• How strong is a statistical syllogism? • Depends on • proportion of As that are premised to be Bs • whatever other information you possess • rule of total evidence © 2018 Taylor & Francis

Rule of Total Evidence • Strength of any inductive argument is determined not just by what’s internal to the argument, but by everything else you know. © 2018 Taylor & Francis

• Defeaters: considerations that tell against accepting a conclusion. • Rebutting defeaters: evidence for thinking the conclusion is false. • Undercutting defeaters: reasons for rejecting the argument that aren’t reasons for rejecting the conclusion. © 2018 Taylor & Francis

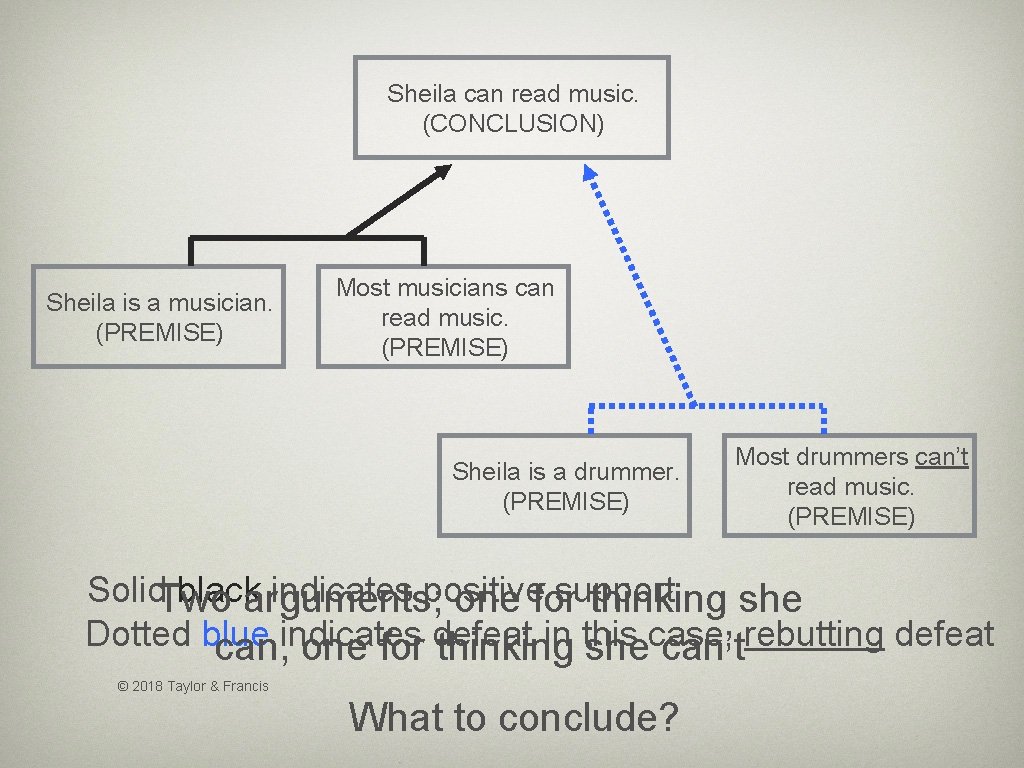
Sheila can read music. (CONCLUSION) Sheila is a musician. (PREMISE) Most musicians can read music. (PREMISE) Sheila is a drummer. (PREMISE) Most drummers can’t read music. (PREMISE) Solid. Two blackarguments; indicates positive support one for thinking she Dotted blue indicates defeat in this case, rebutting defeat can, one for thinking she can’t © 2018 Taylor & Francis What to conclude?

Statistical syllogism • n% of As are Bs. • x is an A. • x is a B. © 2018 Taylor & Francis

Statistical syllogism reference class • n% of As are Bs. • x is an A. • x is a B. © 2018 Taylor & Francis

Statistical syllogism reference class • n% of As are Bs. • x is an A. • x is a B. attribute class We’re attributing B to x, by reference to its being A. © 2018 Taylor & Francis

Statistical syllogism • In the earlier example, Drummer is a narrower reference class than Musician: • all drummers are musicians, but not vice versa. • Use statistical syllogism only for the narrowest reference class for which you have information. • Given our evidence, we should infer that Sheila cannot read music. © 2018 Taylor & Francis

Inductive Generalization © 2018 Taylor & Francis

Inductive generalization • x% of observed As have been Bs. • x% of As are Bs. © 2018 Taylor & Francis

Inductive generalization sample • x% of observed As have been Bs. • x% of As are Bs. © 2018 Taylor & Francis

Inductive generalization sample • x% of observed As have been Bs. • x% of As are Bs. population © 2018 Taylor & Francis

• Sample must be representative of the population. • no systematic difference • large and random • have variety that matches population • homogeneous population • carefully crafted (stratified) sample © 2018 Taylor & Francis

Defeaters for Inductive Generalization © 2018 Taylor & Francis

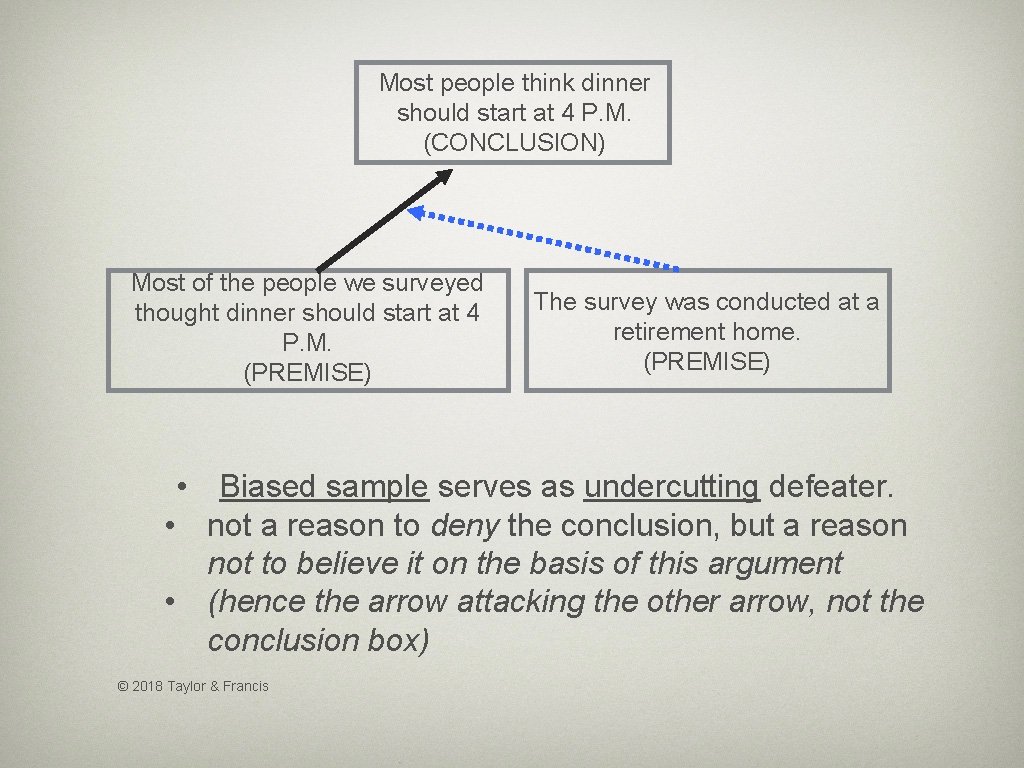
Most people think dinner should start at 4 P. M. (CONCLUSION) Most of the people we surveyed thought dinner should start at 4 P. M. (PREMISE) The survey was conducted at a retirement home. (PREMISE) • Biased sample serves as undercutting defeater. • not a reason to deny the conclusion, but a reason not to believe it on the basis of this argument • (hence the arrow attacking the other arrow, not the conclusion box) © 2018 Taylor & Francis

Fallacies of inductive generalization • Hasty generalization • small sample • Biased statistics • unrepresentative sample • Misleading vividness • relying on anecdotes, rather than inductive generalization © 2018 Taylor & Francis

Fallacies of inductive generalization • Argument from counterinstances • rejecting statistical generalization (“most As are Bs”) on the grounds of one or a few counterinstances (“here’s an A that’s not a B”) • note, this is a legitimate defeater for a universal generalization (“all As are Bs”) © 2018 Taylor & Francis

Representativeness heuristic • (Unreliable) System 1 heuristic for making fast judgments about probabilities, relative frequencies • Probability that something is a member of a group based on how much it resembles a stereotypical member of that group © 2018 Taylor & Francis

Availability heuristic • Another unreliable System 1 heuristic for making fast judgments about probabilities, relative frequencies • Judge how common something is on the basis of how easy it is to think of examples • but easiness is affected by vividness, recently, rarity, etc. • factors other than how common it really is © 2018 Taylor & Francis

Argument From Analogy a. k. a. Analogical argument © 2018 Taylor & Francis

Argument from analogy • x resembles y in known respects. • y has F. • x has F. • Dolphins and whales breathe air, give live birth, and are warm-blooded. • Dolphins lactate. • Whales (probably) lactate. © 2018 Taylor & Francis

Strength of analogical argument • Strength of analogy (degree of similarity) • relevance of similarities • Fallacy of false analogy otherwise © 2018 Taylor & Francis

Inference to the Best Explanation © 2018 Taylor & Francis

Inference to the best explanation • We have such-and-such data. • Hypothesis H • would explain the data, • sufficiently well • and do so better than any rival hypothesis we can think of. • Therefore, H. © 2018 Taylor & Francis

Best explanation? • Genuinely explains • Has some independent plausibility • Is simple and unified • rather than a grab-bag of independent hypotheses • Ockham’s Razor: everything else being equal, we should believe the simpler hypothesis over the more complicated one. © 2018 Taylor & Francis

Balance of Features © 2018 Taylor & Francis

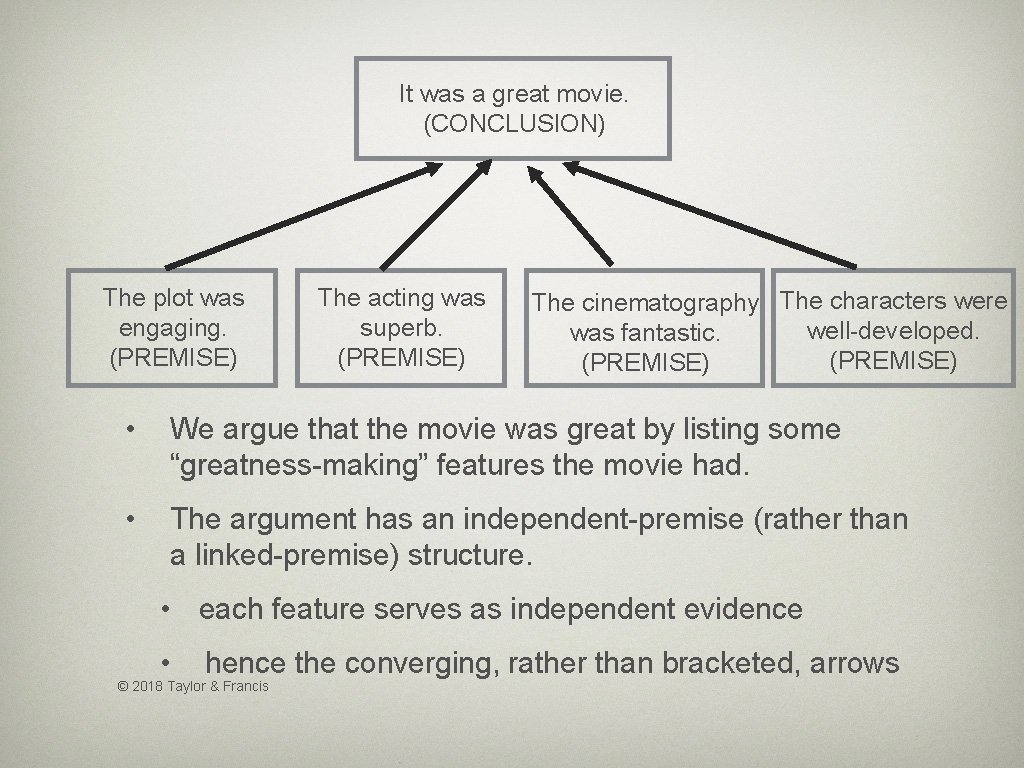
It was a great movie. (CONCLUSION) The plot was engaging. (PREMISE) The acting was superb. (PREMISE) The cinematography The characters were well-developed. was fantastic. (PREMISE) • We argue that the movie was great by listing some “greatness-making” features the movie had. • The argument has an independent-premise (rather than a linked-premise) structure. • each feature serves as independent evidence • hence the converging, rather than bracketed, arrows © 2018 Taylor & Francis

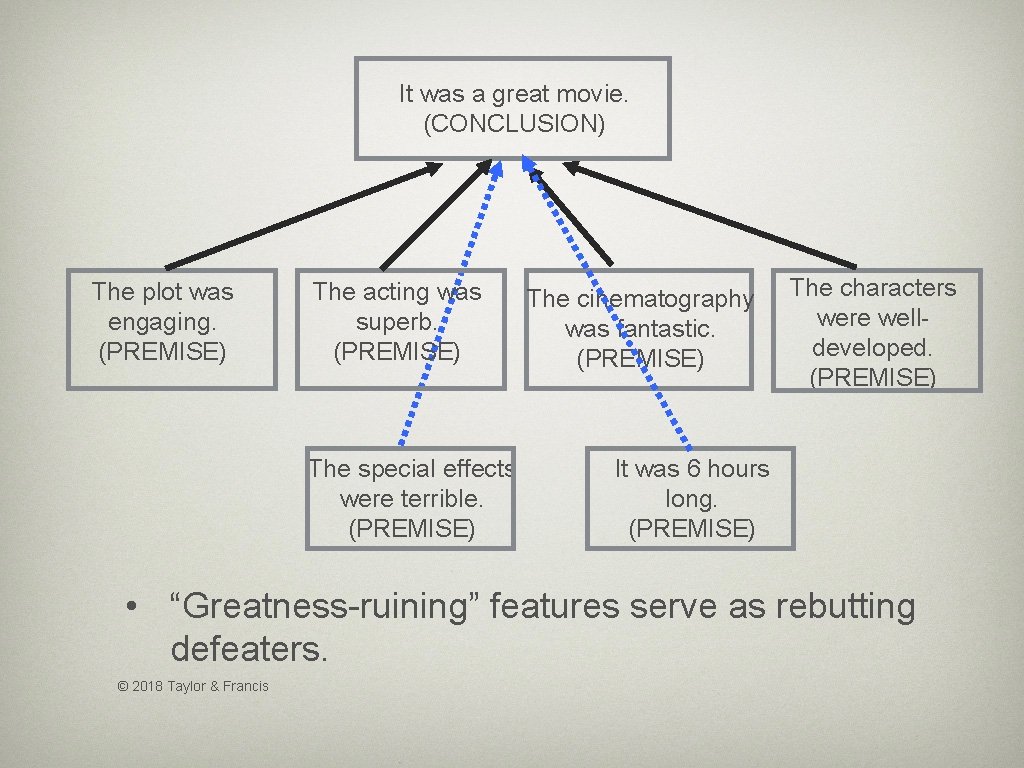
It was a great movie. (CONCLUSION) The plot was engaging. (PREMISE) The acting was superb. (PREMISE) The special effects were terrible. (PREMISE) The cinematography was fantastic. (PREMISE) The characters were welldeveloped. (PREMISE) It was 6 hours long. (PREMISE) • “Greatness-ruining” features serve as rebutting defeaters. © 2018 Taylor & Francis