Induction Variable Analysis with Chains of Recurrences n

Induction Variable Analysis with Chains of Recurrences n Brief tutorial on induction variable recognition ¨ n n Past and present methods for IV detection Chains of recurrences: why and how? Analyzing pointer arithmetic in loops Array dependence testing for loop restructuring and vectorization Results and conclusions Intel 9/12/05 1

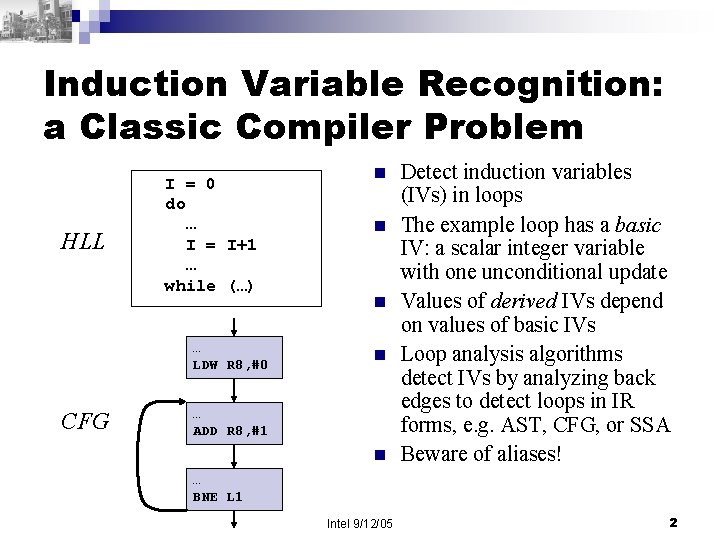
Induction Variable Recognition: a Classic Compiler Problem HLL I = 0 do … I = I+1 … while (…) … LDW R 8, #0 CFG n n … ADD R 8, #1 n Detect induction variables (IVs) in loops The example loop has a basic IV: a scalar integer variable with one unconditional update Values of derived IVs depend on values of basic IVs Loop analysis algorithms detect IVs by analyzing back edges to detect loops in IR forms, e. g. AST, CFG, or SSA Beware of aliases! … BNE L 1 Intel 9/12/05 2

Most Loop Optimizations Rely on Accurate IV Recognition n n Loop strength reduction [Allen 69, Aho 86] IV elimination [Lowry 69, Kennedy 81, Aho 86] IV substitution [Gerlek 95, Haghighat 96, Wolfe 92] Loop iteration bounds analysis Pointer-to-array conversion and array recovery [van. Engelen 01 b, Franke 01] n Array dependence testing for loop restructuring [Banerjee 88, Blume 94, Goff 91, Maydan 91, Muchnick 97, Psarris 03, Pugh 91, van. Engelen 04, Wolfe 92, Zima 90] and others Intel 9/12/05 3

A Classic Induction Variable Recognition Algorithm [Aho 86] n Input: Loop L with reaching definition information and loop-invariant information Output: Triple (i, stride, init) for each IV Find basic IVs: represent basic IV i by triple (i, stride, init) 2. Find derived IVs: search for variables k with single assignment k = j b where b is constant (loop invariant), if j has triple (i, c, d) and = * then k has triple (i, b*c, b*d) else if j has triple (i, c, d) and = + then k has triple (i, c, b+d) (assuming no use of k before its def) 1. Intel 9/12/05 4

IV Recognition for Loop Optimization Example loop with IVs I = 0 J = 1 while (I<N) I = I+1 … = A[J] J = J+2 K = 2*I A[K] = … endwhile IV Triples After strength reduction (I, 1, 0) basic (J, 2, 1) basic (I, 2, 2) derived K = 0 I = 0 J = 1 while (I<N) I = I+1 … = A[J] J = J+2 K = K+2 A[K] = … endwhile Intel 9/12/05 After IV elimination K = 0 while (K<2*N) … = A[K+1] K = K+2 A[K] = … endwhile 5

IV Recognition for Loop Vectorization & Parallelization Example loop with IVs After IV substitution (IVS) After parallelization (note the affine indexes) I = 0 J = 1 while (I<N) I = I+1 … = A[J] IVS J = J+2 K = 2*I A[K] = … endwhile A[] W R A[2*i+1] W R … A[2*i+2] for i=0 to N-1 forall (i=0, N-1) S 1: … = A[2*i+1] S 2: A[2*i+2] = … Dep test A[2*i+2] = … endforall GCD test to solve dependence equation 2 id - 2 iu = -1 Since 2 does not divide 1 there is no data dependence. Intel 9/12/05 6

IV Recognition isn’t Always Trivial … n n n IVs that are linear (affine) but not handled by [Aho 86]: do do K = J+1 J = K+1 while (…) K = 3 K = K+J if (…) J = K else J = J+3 endif while (…) It quickly gets more complicated with deps and flow Note that transformations such as constant propagation, forward substitution, and code motion can help Intel 9/12/05 7

More Powerful IV Recognition Methods n Linear IV recognition on SSA forms and FUD chains [Cytron 91, Wolfe 92] n n n Linear and nonlinear IV recognition with symbolic differencing [Haghighat 95] Linear and nonlinear IV recognition with recurrence system solvers [Gerlek 95] Linear and nonlinear IV recognition with chains of recurrences [van. Engelen 01 a] Intel 9/12/05 8

A Method for Linear IV Recognition on FUD Chains n n n Similar algorithms by [Cytron 91, Wolfe 92] Factored use-def (FUD) chains are similar to single static assignment (SSA) forms Input: FUD chains Output: Triple (i, stride, init) for each IV Build depth-first spanning tree of operations 2. Start at -node in loop cycle to find basic IVs 3. Find derived IVs from other -nodes not in a cycle 1. Intel 9/12/05 9

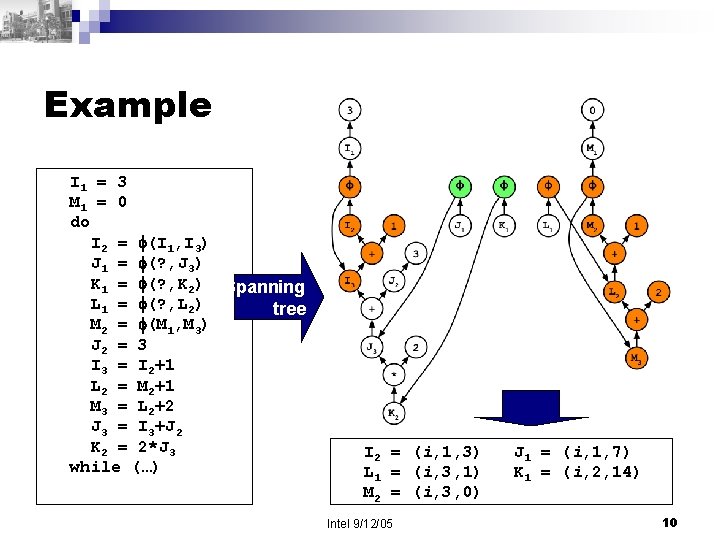
Example I 1 = 3 M 1 = 0 do I 2 = (I 1, I 3) J 1 = (? , J 3) K 1 = (? , K 2) Spanning L 1 = (? , L 2) tree M 2 = (M 1, M 3) J 2 = 3 I 3 = I 2+1 L 2 = M 2+1 M 3 = L 2+2 J 3 = I 3+J 2 K 2 = 2*J 3 while (…) I 2 = (i, 1, 3) L 1 = (i, 3, 1) M 2 = (i, 3, 0) Intel 9/12/05 J 1 = (i, 1, 7) K 1 = (i, 2, 14) 10

Symbolic Differencing Use abstract interpretation to evaluate loop iterations and construct symbolic difference table of the IV values. do x = y = z = while x+z z+1 y+1 (…) Iteration x 1 x+z diff 2 x+2 z+2 3 x+3 z+6 z+4 y z z+1 diff z+3 2 z+2 2 2 z+5 2 z+4 2 From difference tables compute the characteristic functions describing the IV progressions. Intel 9/12/05 x(i) = x 0 + z 0 i + (i 2 -i) y(i) = z 0 + 2 i + 1 z(i) = z 0 + 2 i 11

Symbolic Differencing: Oops [van. Engelen 01 a] identified a serious problem with the differencing method for IVs involving cyclic recurrence relations. The inferred closed-form function might be incorrect when it is assumed that the polynomial order of the IVs is bounded. Quiz: guess the maximum polynomial order of the characteristic functions of the IVs shown in the loop on the right. Intel 9/12/05 ? for i=0 to n t = a a = b b = c+2*b-t+2 c = c+d d = d+i endfor 12

Outline n n Brief tutorial on induction variable recognition Chains of recurrences: why and how? Chains of recurrences preliminaries [Zima 92, van. Engelen 01 a] ¨ Chains of recurrences for IV recognition, loop analysis, and optimization [van. Engelen 01 a, van. Engelen 01 b, van. Engelen 04] ¨ n n n Analyzing pointer arithmetic in loops Array dependence testing for loop restructuring and vectorization Results and conclusions Intel 9/12/05 13

Preliminaries n n A chain of recurrences (CR) represents a polynomial or exponential function or mix evaluated over a unit-distance grid [Zima 92] Basic form: {init, , stride} Iteration {init, , stride} f(i) = 2 i+1 = {1, +, 2} f(i) = 2 i = {1, *, 2} i = 0 init 1 1 i = 1 init stride 3 2 i = 2 init stride 5 4 i = 3 init stride 7 8 Intel 9/12/05 14

Chains of Recurrences: General Formulation n n The key idea is to represent a non-constant CR stride in CR form itself, thereby forming a chain of recurrences Example: f(i) = i 2 = {0, +, s(i-1)} with s(i) = {1, +, 2} Iteration {init, , s(i-1)} s(i) = {1, +, 2} f(i) = {0, +, s(i-1)} i = 0 init 1 0 i = 1 init s(0) 3 1 i = 2 init s(0) s(1) 5 4 i = 3 init s(0) s(1) s(2) 7 9 Intel 9/12/05 15

Primary Application of CRs: Loop Strength Reduction n Loop strength reduction is straight forward to implement with CR forms of real-valued and complex functions [Zima 92] n Method: add each CR and its nested CR stride as IVs to the loop nest Intel 9/12/05 16

Example n n n Suppose f(i) = a + b·i + c·i 2 = {a, +, {b+c, +, 2 c}} We have two IVs x and y: s(i) f(i) = x = {x 0, +, y} with x 0 = a s(i) = y = {y 0, +, 2 c} with y 0 = b+c Add x and y as IVs to loop for efficient function evaluation over unit-distance grid i = 0, …, n : x = a y = b+c for i=0 to n f[i] = x x = x+y y = y+2*c endfor Intel 9/12/05 17

Loop Strength Reduction: Multi-dimensional Loops n Algorithm for 2 -d case (n-d similar) Determine iteration order: for i = 0 to n for j = 0 to m 2. Compute CR forms for j-loop first by treating i invariant within j-loop 3. Compute multivariate CR (MCR) forms for i-loop 1. Intel 9/12/05 18

Example n Suppose f(i, j) = i 2 + i·j + 1 Create IV k for f(i, j) in j-loop: f(i, j) = kj = {pi, +, ri}j with pi = i 2 + 1 and ri = i 2. Create IVs for pi and ri in i-loop: pi = {p 0, +, qi}i with p 0 = 1 qi = {q 0, +, 2}i with q 0 = 1 ri = {r 0, +, 1}i with r 0 = 0 3. Add IVs k, p, q, and r to loops 1. Intel 9/12/05 p = 1 q = 1 r = 0 for i = 0 to n k = p for j = 0 to m f[i, j] = k k = k+r endfor p = p+q q = q+2 r = r+1 endfor 19

How to Obtain CR Forms for Strength Reduction: CR Algebra n Algorithm to compute the CR form of a symbolic function f(i): 1. 2. n Replace i with {0, +, 1} in the symbolic form of f Compute CR form using the CR algebra rewrite rules (selected rules shown here): {x, +, y} + c {x+c, +, y} c{x, +, y} {c·x, +, c·y} {x, +, y} + {u, +, v} {x+u, +, y+v} {x, +, y} * {u, +, v} {x·u, +, y{u, +, v}+v{x, +, y}+y·v} Example: f(i) = c·(i+a) = c·({0, +, 1}+a) = c{a, +, 1} = {c·a, +, c} Intel 9/12/05 20

But What About IV Recognition? n The key idea of our approach: Scan the loop to detect IV updates ¨ Determine the CR form of the IV using the update operation ¨ n In simple terms, the method looks for operations on IVs that can be represented as CR forms: do J = I = P = while J+I I+3 2*P (…) J = {J 0, +, I} I = {I 0, +, 3} P = {P 0, *, 2} Intel 9/12/05 J = {J 0, +, {I 0, +, 3}} 21

Compiler Algorithms for IV Recognition with CRs n IV recognition algorithms [van. Engelen 01 a, van. Engelen 04] : Scan the loop in backward order to determine recurrence relations of scalar variables in the loop 2. Compute CR forms of recurrence relations 3. “Solve” CR forms by computing closed-form characteristic functions with the CR inverse rules 1. n Note: GCC 4. x uses this algorithm first published in [van. Engelen 01 a] applied to loops in SSA form. GCC developers refer to CRs as “scalar evolutions” (without proper justification). Intel 9/12/05 22

Algorithm 1: Find Recurrences n Input: Loop L with live variable information Output: Set S of recurrence relations of IVs Start with set S = { v, v | v is live at loop header } 2. Search L from bottom to top: for each assignment v = x of expression x to scalar variable v update tuples u, y in S by replacing v in y with x 1. Loop L Step S = { H, H , I, I , J, J , K, K } do M = L = J = K = I = while 2 J-H L+M K+M*I I+1 (…) 5 4 3 2 1 S 5 = { H, H , I, I+1 , J, J-H+2 , K, K+2*I } S 4 = { H, H , I, I+1 , J, J-H+M , K, K+M*I } S 3 = { H, H , I, I+1 , J, L+M , K, K+M*I } S 2 = { H, H , I, I+1 , J, J , K, K+M*I } S 1 = { H, H , I, I+1 , J, J , K, K } Intel 9/12/05 23

Algorithm 2: Compute CR Forms n Input: Set S with recurrence relations Output: CR forms for IVs in S For each relation v, x in S do: if x is of the form v then v = v 0 (v is loop invariant) if x is of the form v + y then v = {v 0, +, y} if x is of the form v * y then v = {v 0, *, y} if x does not contain v then v = {v 0, #, y} (v is wrap around) 2. Simplify the CR forms with the CR algebra rewrite rules 1. Recurrence relation in S H, H I, I+1 J, J-H+2 K, K+2*I CR form H = H 0 I = {I 0, +, 1} J = {J 0, +, 2 -H} K = {K 0, +, 2*I} Intel 9/12/05 Simplified CR form H = H 0 I = {I 0, +, 1} J = {J 0, +, 2 -H 0} K = {K 0, +, 2 I 0, +, 2} 24

Algorithm 3: Solve n Input: CR forms for IVs Output: Closed-form solutions for IVs (when possible) For each CR form of v apply the CR inverse algebra, assuming loop is normalized for i = 0, …, n 2. Certain “exotic” mixed non-polynomial and nonexponential CR forms may not have closed forms 1. Loop L Simplified CR form for i = 0, … do M = L = J = K = I = while Closed form 2 J-H L+M K+M*I I+1 (…) J = {J 0, +, 2 -H 0} K = {K 0, +, 2 I 0, +, 2} I = {I 0, +, 1} Intel 9/12/05 J = J 0 + (2 -H 0)*i K = K 0 + i 2 + (2 I 0 -1)*i I = I 0 + i 25

Example 1 Loop L do x = y = z = while x+z z+1 y+1 (…) Step S = { x, x , z, z } 3 S 3 = { x, x+z , z, z+2 } 2 S 2 = { x, x , z, z+2 } 1 S 1 = { x, x , z, y+1 } Intel 9/12/05 CR form x = {x 0, +, z} z = {z 0, +, 2} Closed form x(i) = x 0 + z 0 i + i 2 -i z(i) = z 0+2 i 26

Example 2 DO I=1, M DO J=1, I ij = ij+1 ijkl = ijkl+I-J+1 DO K=I+1, M DO L=1, K ijkl = ijkl+1 xijkl[ijkl]=xkl[L] IVS ENDDO ijkl = ijkl+ij+left ENDDO TRFD code segment from Perfect Benchmark with IV updates DO I=0, M-1 DO J=0, I DO K=0, M-I-2 DO L=0, I+K+1 tmp = ijkl+L+I*(K+(M+M*M+2*left+6)/4 )+J*(left+(M+M*M)/2)+((I*I*M*M )+2*(K*K+3*K+I*I*(left+1))+M*I *I)/4+2 xijkl[tmp] = xkl[L+1] ENDDO TRFD after aggressive induction variable substitution Intel 9/12/05 27

Recognizing Mixed Functional Forms and Reductions Loop L I = 1 do F = F*I I = I+1 while (…) Loop L I = 0; S = 0 do S = S+A[I] I = I+2 while (…) Simplified CR form F = {F 0, *, 1, +, 1} I = {1, +, 1} Factorial F = F 0 * i! Simplified CR form Reduction S = {0, +, A[{0, +, 2}]} I = {0, +, 2} S = ∑ A[2 i] Intel 9/12/05 28

Outline n n n Brief tutorial on induction variable recognition Chains of recurrences: why and how? Analyzing pointer arithmetic in loops ¨ n n Converting pointer references into array references to facilitate array dependence testing and loop restructuring Array dependence testing for loop restructuring and vectorization Results and conclusions Intel 9/12/05 29

Converting Pointer References to Array References n n n Key observation: pointers with pointer arithmetic in loops often behave similar to IVs Use IV recognition algorithms to detect pointerbased IVs Convert pointer-based IVs to closed-form characteristic functions to obtain array references Intel 9/12/05 30

Pointer Access Descriptions of Pointer and Array References n n A pointer access description (PAD) [van. Engelen 01 b] is a CR form of a pointer or array reference in a loop nest PADs are computed with the CR-based IV algorithms short a[…], *p; int i; p = a; for(i=0; …; i++) { } Loop Code PAD Sequence a[i] {a, +, 1} a[0], a[1], a[2], a[3] a[2*i+1] {a+1, +, 2} a[1], a[3], a[5], a[7] a[(i*i-i)/2] {a, +, 0, +, 1} a[0], a[1], a[3] a[1<<i] {a+1, +, 1, *, 2} a[1], a[2], a[4], a[8] p++ {a, +, 1} a[0], a[1], a[2], a[3] p+=i {a, +, 0, +, 1} a[0], a[1], a[3] Intel 9/12/05 31

Example f += 2; lsp += 2; for (i = 2; i <= 5; i++) { *f = f[-2]; for (j = 1; j < i; j++, f--) *f += f[-2]-2*(*lsp)*f[-1]; *f -= 2*(*lsp); f += i; lsp += 2; } Lsp_az speech codec segment from ETSI with pointer updates. Intel 9/12/05 for (i = 0; i <= 3; i++) { f[i+2] = f[i]; for (j = 0; j <= i; j++) f[i-j+2] += f[i-j]2*lsp[2*i+2]*f[i-j+1]; f[1] -= 2*lsp[2*i+2]; } Lsp_az speech codec segment after pointer-to-array conversion. Note that all array index expressions are affine. 32

Outline n n Brief tutorial on induction variable recognition Chains of recurrences: why and how? Analyzing pointer arithmetic in loops Array dependence testing for loop restructuring and vectorization CR-based dependence testing ¨ Solving linear (affine), nonlinear, and symbolic equations ¨ n Results and conclusions Intel 9/12/05 33

Benefits of Array & Pointer Dependence Testing with CRs n Reduced complexity of testing Eliminates IV substitution phase ¨ Eliminates the need for pointer-to-array conversion for dependence testing on pointer-based C code ¨ n Extended coverage Able to solve linear, nonlinear, and symbolic dependence equations ¨ Possibility to augment existing tests, such as the extreme value test and range test ¨ Intel 9/12/05 34

CR Dependence Equations n n n Compute dependence equations in CR form for pointer and array accesses in loop nests directly without IV substitution or pointer-to-array conversion Solve the equations by computing value ranges of the CR forms to determine solution intervals If the solution space is empty, there is no dependence Intel 9/12/05 35

Determining the Value Range of a CR Form on a Domain n Suppose x(i) = {x 0, +, s(i-1)} for i = 0, …, n If s(i-1) > 0 then x(i) is monotonically increasing ¨ If s(i-1) < 0 then x(i) is monotonically decreasing ¨ n If a function is monotonic on its domain, then it is trivial to find its exact value range Intel 9/12/05 36

Example n Determine the value range of x(i) = (i 2 -i)/2 for i = 0, …, 10 Convert to CR form x(i) = {0, +, 1}} ¨ Monotonically increasing, since {0, +, 1} = i > 0 for i = 0, …, 10 ¨ Therefore, lower bound of x(i) is x(0) = 0 and upper bound is x(10) = (102 -10)/2 = 45 ¨ n Classic interval analysis often gives conservative results ¨ For this example, interval analysis gives the range ([0, 10]2 -[0, 10])/2 = ([0, 100]+[-10, 0])/2 = [-10, 100]/2 = [-5, 50] Intel 9/12/05 37

Solving a Dependence Equation float a[…], *p, *q; p = a; q = a+2*n; for (i=0; i<n; i++) { t = *p; S: *p++ = *q; *q-- = t; } S * p={a, +, 1} q={a+2 n, +, -1} Dependence equation: {a, +, 1}id = {a+2 n, + , -1}iu Constraints: 0 < id < n-1 0 < iu < n-1 Compute solution interval: Low[{{-2 n, +, 1}iu, +, 1}id] = Low[{-2 n, +, 1}iu] = -2 n Up[{{-2 n, +, 1}iu, +, 1}id] = Up[{-2 n, +, 1}iu + n-1] = Up[-2 n + 2 n - 2] = -2 Rewrite dependence equation: {a, +, 1}id = {a+2 n, +, -1}iu {a, +, 1}id - {a+2 n, +, -1}iu = 0 {{-2 n, +, 1}iu, +, 1}id = 0 No dependence Intel 9/12/05 38

Dependence Testing on Nonlinear & Symbolic Accesses float a[…], *p, *q; p = q = a; for (i=0; i<n; i++) { for (j=0; j<=i; j++) *q += *++p; q++; } DO i = 1, M+1 S 1: A[I*N+10] =. . . S 2: . . . = A[2*I+K] K = 2*K+N ENDDO p = {{a+1, +, 1}i, +, 1}j = a[(i 2+i)/2+j+1] q = {a, +, 1}i = a[i] S 1: A[{N+10, +, N}i] S 2: A[{K 0+2 N, +, K 0+ N+2, *, 2}i] CR range test disproves dependence when CR dep. test disproves flow dependence (<, <) K+N > 10 and K > 2 Intel 9/12/05 39

Some Observations wrt. Vectorization n n Auto-vectorization (mostly) requires affine array accesses, e. g. to enable unimodular loop transformations Best when vector loads/stores are memory aligned Data remapping possible, but runtime remapping may outweigh vectorization speedup CR forms of array and pointer accesses naturally represent memory access sequences, which may help in detecting aligned memory accesses and to support data remapping Intel 9/12/05 40

Some Preliminary Results Perfect Club Suite Benchmark Additional dependence pairs broken by CR test over Omega and range test DYFESM* OCEAN QCD* BDNA TRFD MDG* MG 3 D* 0 63 51 6 10 62 8 Results shown produced from CR test implementation in Polaris *Test results incomplete due to Polaris memory issue Intel 9/12/05 41

Conclusions n The CR-based compiler analysis framework supports: ¨ ¨ ¨ n IV recognition and strength reduction optimizations Pointer-to-array conversion for analysis of C loops Array dependence testing with affine, nonlinear, and symbolic dependence equations Dependence testing on pointer arithmetic Induction variable substitution Implementations GCC 4. x (with limitations!) ¨ From our lab: Polaris (TBA) ¨ Intel 9/12/05 42

Further Reading n n Robert van Engelen, Johnnie Birch, Yixin Shou, Burt Walsh, and Kyle Gallivan, “A Unified Framework for Nonlinear Dependence Testing and Symbolic Analysis”, in the proceedings of the ACM International Conference on Supercomputing (ICS), 2004, pages 106 -115. Robert van Engelen, Johnnie Birch, and Kyle Gallivan, “Array Dependence Testing with the Chains of Recurrences Algebra”, in the proceedings of the IEEE International Workshop on Innovative Architectures for Future Generation High. Performance Processors and Systems (IWIA), January 2004, pages 70 -81. Robert van Engelen and Kyle Gallivan, “An Efficient Algorithm for Pointer-to. Array Access Conversion for Compiling and Optimizing DSP Applications”, in proceedings of the 2001 International Workshop on Innovative Architectures for Future Generation High-Performance Processors and Systems (IWIA), January 2001, pages 80 -89. Robert van Engelen, “Efficient Symbolic Analysis for Optimizing Compilers”, in proceedings of the International Conference on Compiler Construction, ETAPS 2001, LNCS 2027, pages 118 -132. Intel 9/12/05 43

References [Aho 86] [Allen 69] [Bannerjee 88] [Blume 94] [Cytron 91] [Franke 01] [Gerlek 95] [Goff 91] [Haghighat 95] [Kennedy 81] [Lowry 69] [Maydan 91] [Muchnick 97] [Psarris 03] [Pugh 91] [van. Engelen 01 a] [van. Engelen 01 b] [van. Engelen 04] [Wolfe 92] [Wolfe 96] [Zima 90] [Zima 92] AHO, A. , SETHI, R. , AND ULLMAN, J. Compilers: Principles, Techniques and Tools. Addison-Wesley Publishing Company, Reading MA, 1985. ALLEN, F. E. Program optimization, Annual Review in Automatic Programming, 5, pp. 239 -307. BANERJEE, U. Dependence Analysis for Supercomputing. Kluwer, Boston, 1988. BLUME, W. , AND EIGENMANN, R. The range test: a dependence test for symbolic non-linear expressions. In proceedings of Supercomputing (1994), pp. 528– 537. 22, 2 (1994), 183– 205. CYTRON, R. , FERRANTE, J. , ROSEN B. K, WEGMAN, M. N, ZADECK, F. K. Efficiently Computing Static Single Assignment Form and the Control Dependence Graph, ACM Transactions on Programming Languages and Systems, 1991 FRANKE, B. , AND O’BOYLE, M. Compiler transformation of pointers to explicit array accesses in DSP applications. In proceedings of the ETAPS Conference on Compiler Construction 2001, LNCS 2027 (2001), pp. 69– 85. GERLEK, M. , STOLZ, E. , AND WOLFE, M. Beyond induction variables: Detecting and classifying sequences using a demand-driven SSA form. ACM Transactions on Programming Languages and Systems (TOPLAS) 17, 1 (Jan. 1995), pp. 85– 122. GOFF, G. , KENNEDY, K. , AND TSENG, C. -W. Practical dependence testing. In proceedings of the ACM SIGPLAN’ 91 Conference on Programming Language Design and Implementation (PLDI) (1991), vol. 26, pp. 15– 29. HAGHIGHAT, M. R. Symbolic Analysis for Parallelizing Compilers. Kluwer Academic Publishers, 1995. KENNEDY, K. A survey of data flow analysis techniques, in Muchnick and Jones, (1981), pp. 5 -54. LOWRY. E. S. AND MEDLOCK C. W. Object code optimization, Communications of the ACM, 12, ( 1991), pp. 159 -166. MAYDAN, D. E. , HENNESSY, J. L. , AND LAM, M. S. Efficient and exact data dependence analysis. In proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI) (1991), ACM Press, pp. 1– 14. MUCHNICK, S. Advanced Compiler Design and Implementation. Morgan Kaufmann, San Fransisco, CA, 1997. PSARRIS, K. Program analysis techniques for transforming programs for parallel systems. Parallel Computing 28, 3 (2003), 455– 469. PUGH, W. , AND WONNACOTT, D. Eliminating false data dependences using the Omega test. In proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI) (1992), pp. 140– 151. VAN ENGELEN, R. Efficient symbolic analysis for optimizing compilers. In proceedings of the ETAPS Conference on Compiler Construction, LNCS 2027 (2001), pp. 118– 132. VAN ENGELEN, R. , AND GALLIVAN, K. An efficient algorithm for pointer-to-array access conversion for compiling and optimizing DSP applications. In proceedings of the International Workshop on Innovative Architectures for Future Generation High-Performance Processor and Systems (IWIA) (2001), pp. 80– 89. VAN ENGELEN, R. A. , BIRCH, J. , SHOU, Y. , WALSH, B. , AND GALLIVAN, K. A. A unified framework for nonlinear dependence testing and symbolic analysis. In proceedings of the ACM International Conference on Supercomputing (ICS) (2004), pp. 106– 115. WOLFE, M. Beyond induction variables. In ACM SIGPLAN’ 92 Conf. on Programming Language Design and Implementation (1992), pp. 162– 174. WOLFE, M. High Performance Compilers for Parallel Computers. Addison-Wesley, Redwood City, CA, 1996. ZIMA, H. , AND CHAPMAN, B. Supercompilers for Parallel and Vector Computers. ACM Press, New York, 1990. ZIMA, E. Recurrent relations and speed-up of computations using computer algebra systems. In proceedings of DISCO’ 92 (1992), LNCS 721, pp. 152– 161. Intel 9/12/05 44