Induction of Decision Trees An Example Data Set

Induction of Decision Trees

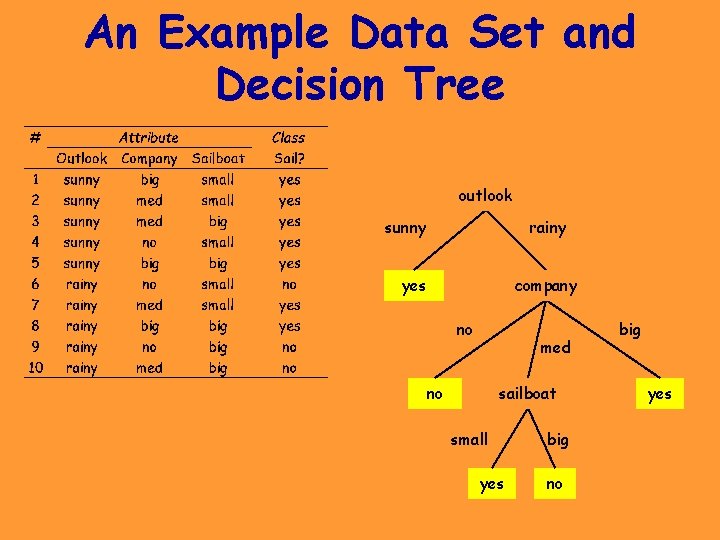
An Example Data Set and Decision Tree outlook sunny rainy yes company no med no sailboat small yes big no big yes

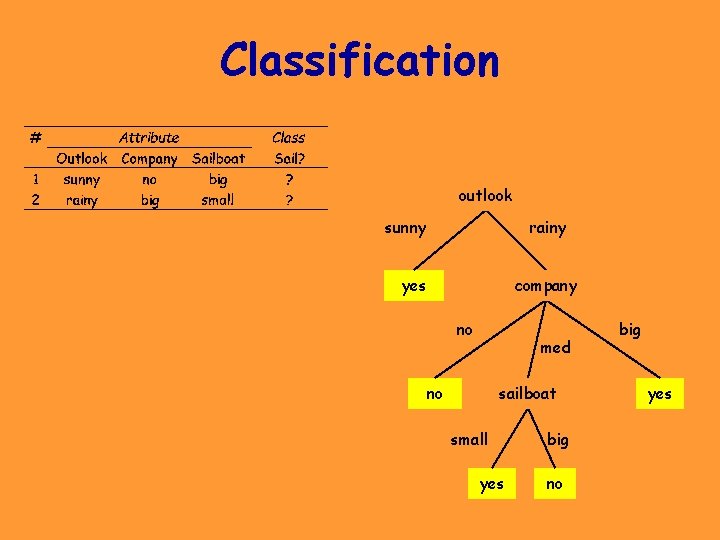
Classification outlook sunny rainy yes company no med no sailboat small yes big no big yes

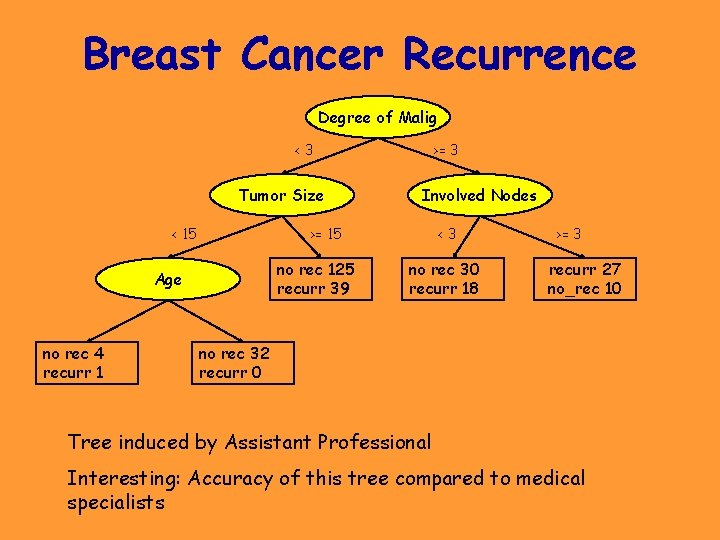
Breast Cancer Recurrence Degree of Malig <3 Tumor Size < 15 Involved Nodes >= 15 no rec 125 recurr 39 Age no rec 4 recurr 1 >= 3 <3 no rec 30 recurr 18 >= 3 recurr 27 no_rec 10 no rec 32 recurr 0 Tree induced by Assistant Professional Interesting: Accuracy of this tree compared to medical specialists

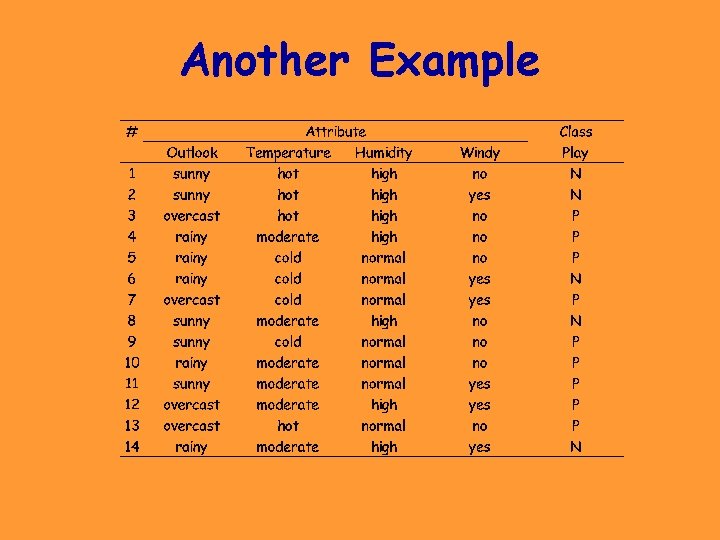
Another Example

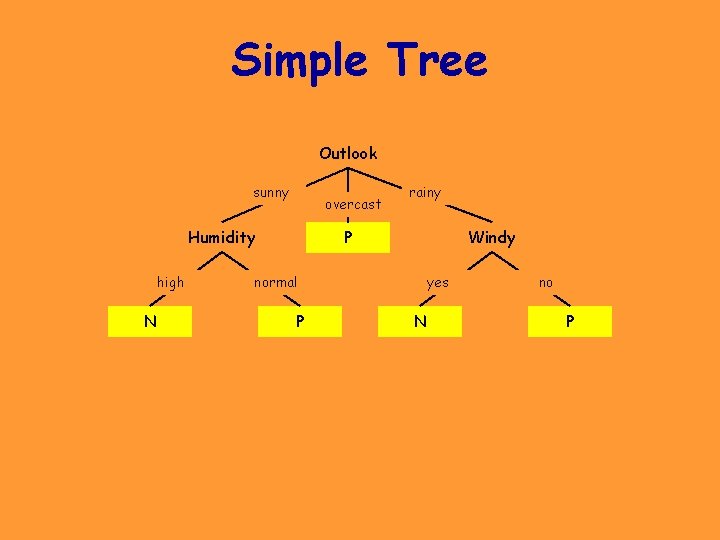
Simple Tree Outlook sunny overcast Humidity high N rainy P Windy normal P yes N no P

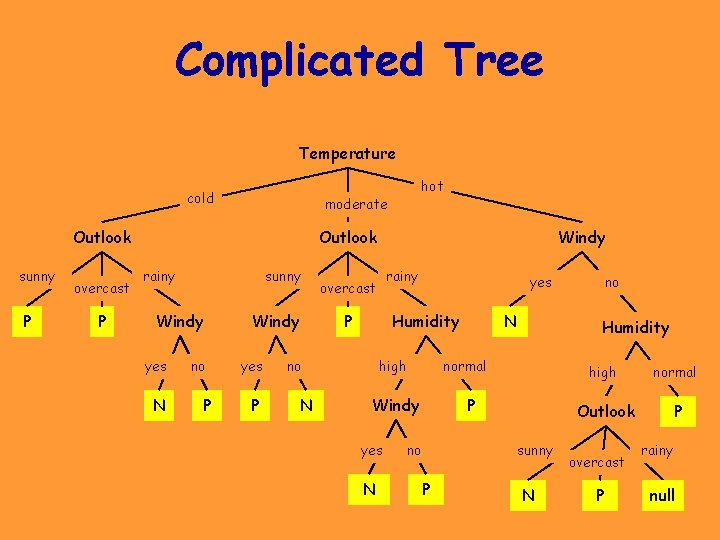
Complicated Tree Temperature cold moderate Outlook sunny P overcast P hot Outlook rainy sunny Windy yes N no P Windy yes P Windy rainy overcast P Humidity no N yes high N Humidity normal Windy yes N P no sunny P no N high normal Outlook P overcast P rainy null

Attribute Selection Criteria • Main principle – Select attribute which partitions the learning set into subsets as “pure” as possible • Various measures of purity – – – Information-theoretic Gini index X 2 Relief. F. . .

Information-Theoretic Approach • To classify an object, a certain information is needed – I, information • After we have learned the value of attribute A, we only need some remaining amount of information to classify the object – Ires, residual information • Gain – Gain(A) = I – Ires(A) • The most ‘informative’ attribute is the one that minimizes Ires, i. e. , maximizes Gain

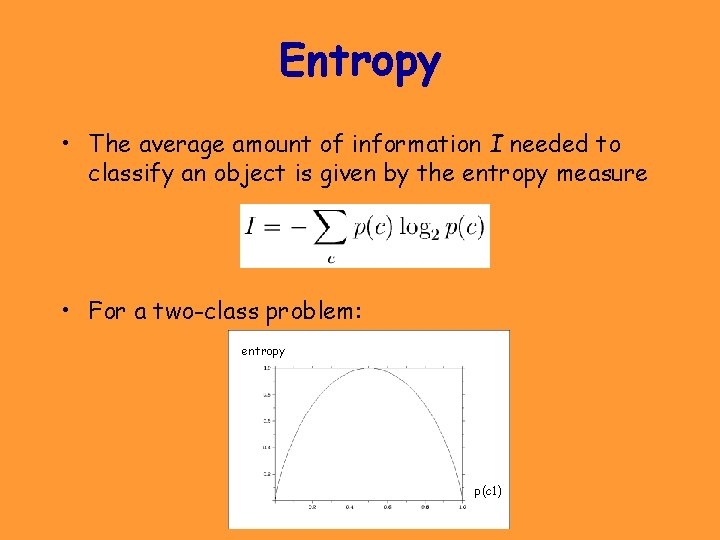
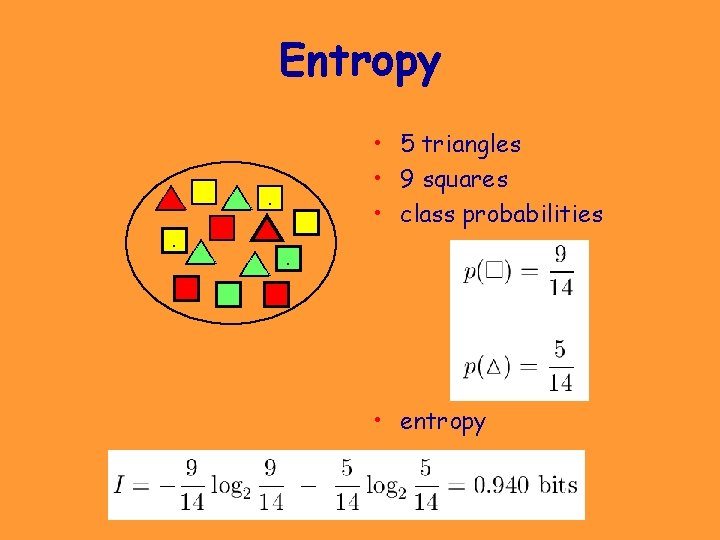
Entropy • The average amount of information I needed to classify an object is given by the entropy measure • For a two-class problem: entropy p(c 1)

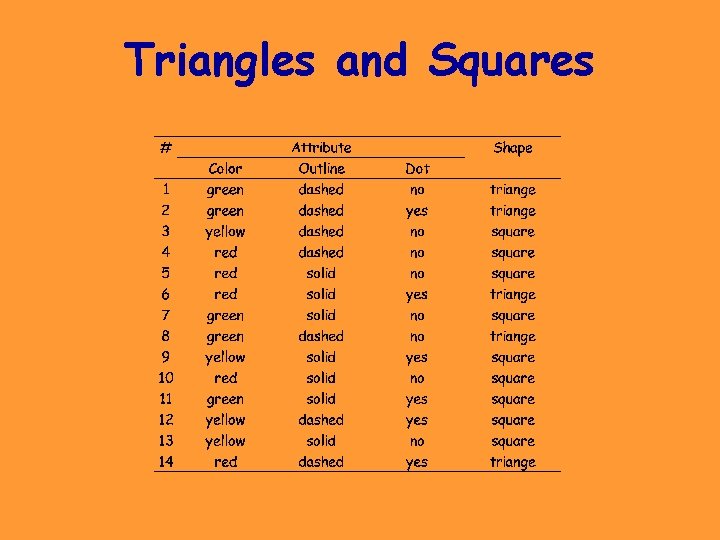
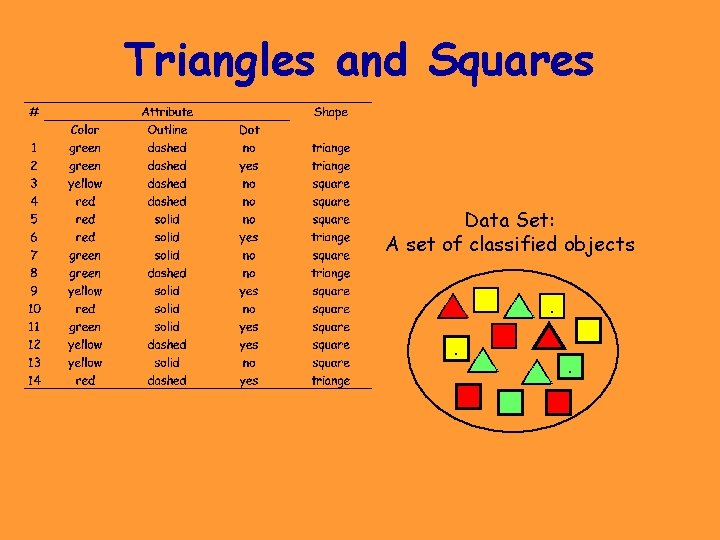
Triangles and Squares

Triangles and Squares Data Set: A set of classified objects. . .

Entropy. . . • 5 triangles • 9 squares • class probabilities. • entropy

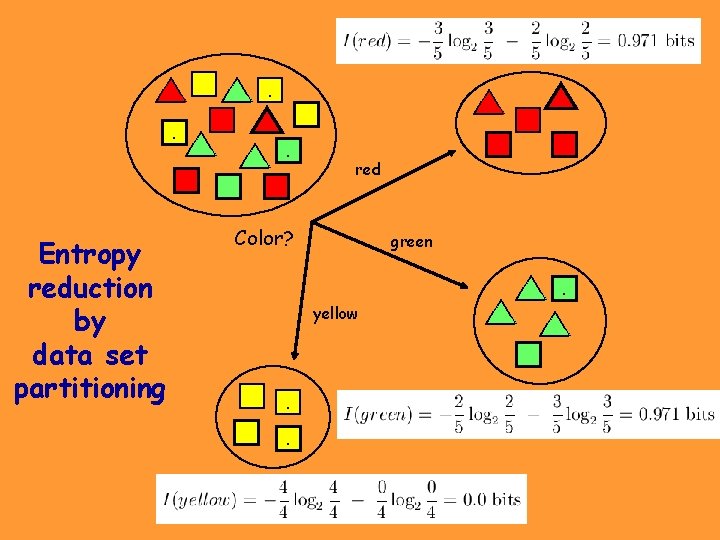
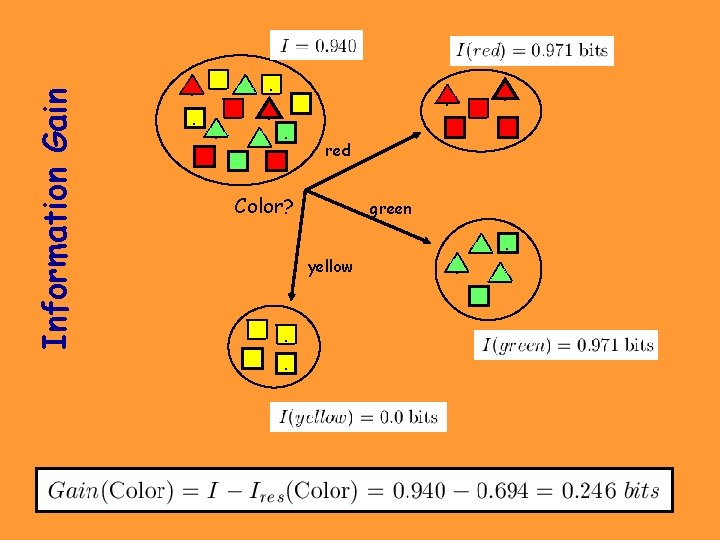
Entropy reduction by data set partitioning . . . . red Color? green . yellow . . .

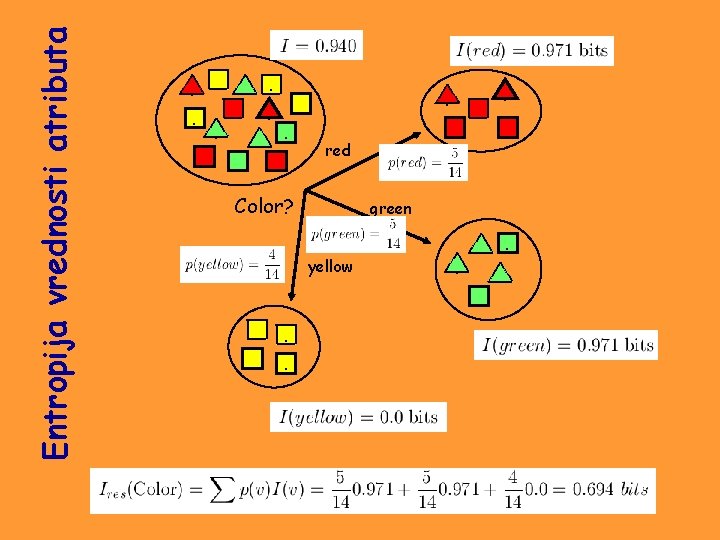
Entropija vrednosti atributa . . . . red Color? green yellow . .

Information Gain . . . . red Color? green yellow . .

Information Gain of The Attribute • Attributes – Gain(Color) = 0. 246 – Gain(Outline) = 0. 151 – Gain(Dot) = 0. 048 • Heuristics: attribute with the highest gain is chosen • This heuristics is local (local minimization of impurity)

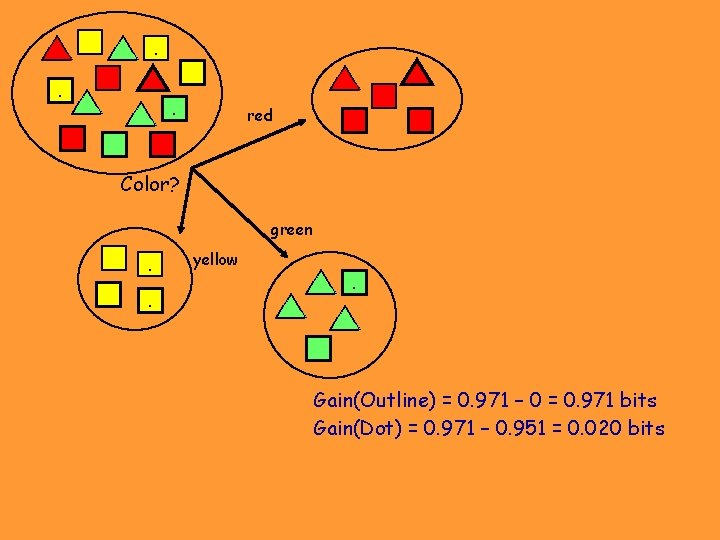
. . . . red Color? green . . yellow . . Gain(Outline) = 0. 971 – 0 = 0. 971 bits Gain(Dot) = 0. 971 – 0. 951 = 0. 020 bits

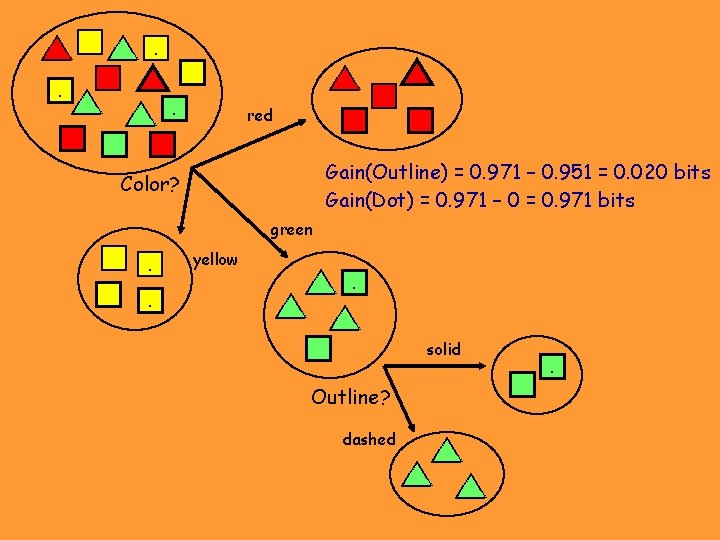
. . . . red Gain(Outline) = 0. 971 – 0. 951 = 0. 020 bits Gain(Dot) = 0. 971 – 0 = 0. 971 bits Color? green . . yellow . . solid Outline? dashed . .

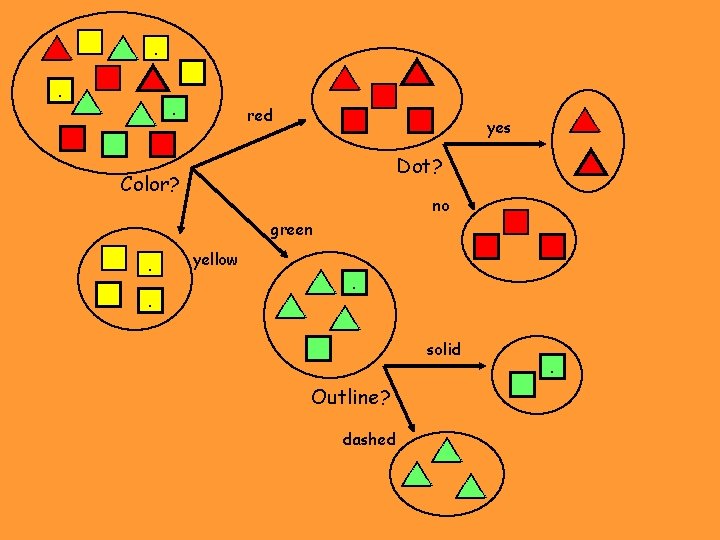
. . . . red . yes Dot? Color? . no green . . yellow . . solid Outline? dashed . .

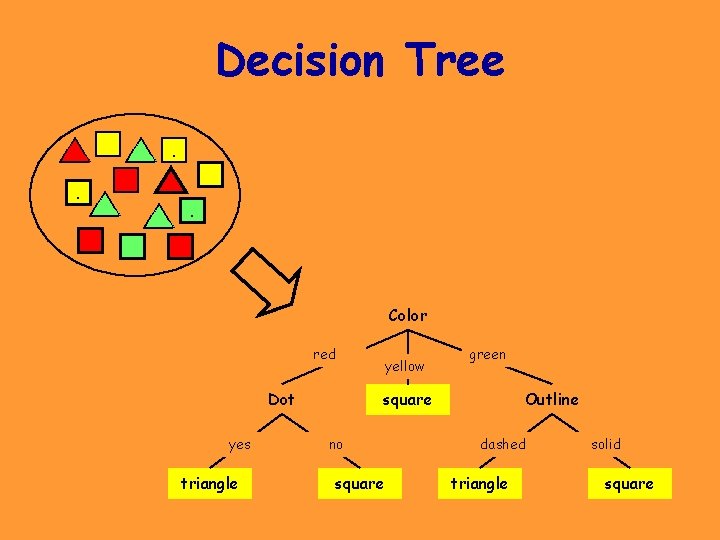
Decision Tree. . . Color red Dot yes triangle yellow green square no square Outline dashed triangle solid square

Gini Index • Another sensible measure of impurity (i and j are classes) • After applying attribute A, the resulting Gini index is • Gini can be interpreted as expected error rate

Gini Index. . .

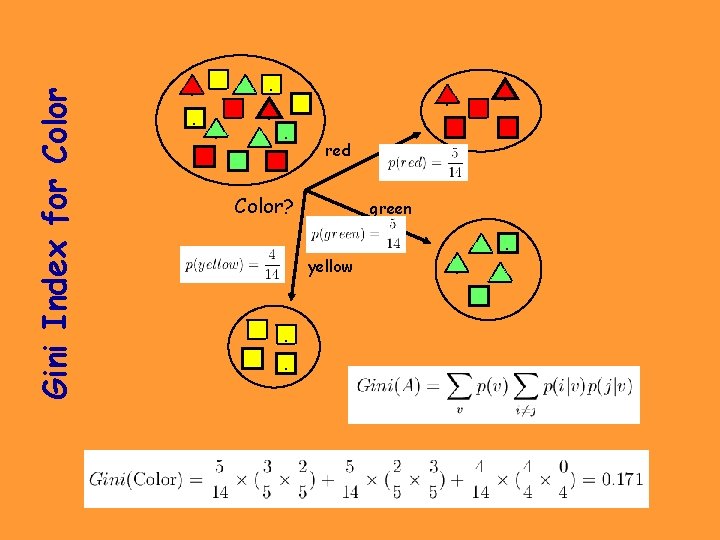
Gini Index for Color . . . . red Color? green yellow . .

Gain of Gini Index

Three Impurity Measures • These impurity measures assess the effect of a single attribute • Criterion “most informative” that they define is local (and “myopic”) • It does not reliably predict the effect of several attributes applied jointly