Induction Fall 2006 11 11 06 Induction Fall










































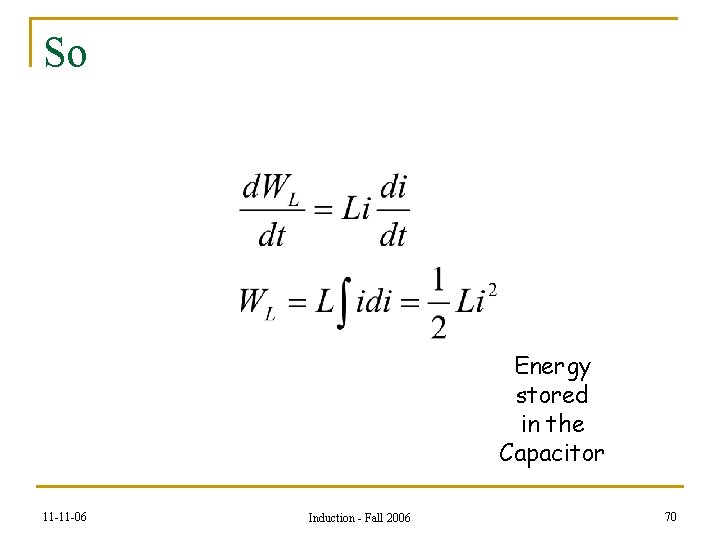




- Slides: 76

Induction Fall 2006 11 -11 -06 Induction - Fall 2006 1

Magnetic Flux For a CLOSED Surface we might expect this to be equal to some constant times the enclosed poles … but there ain’t no such thing! CLOSED SURFACE 2 Induction - Fall 2006 11 -11 -06

Examples S 3 N Induction - Fall 2006 11 -11 -06

A puzzlement. . Let’s apply this to the gap of a capacitor. 4 Induction - Fall 2006 11 -11 -06

Consider the poor little capacitor… i i CHARGING OR DISCHARGING …. HOW CAN CURRENT FLOW THROUGH THE GAP In a FIELD description? ? 5 Induction - Fall 2006 11 -11 -06

Through Which Surface Do we measure the current for Ampere’s Law? I=0 6 Induction - Fall 2006 11 -11 -06

In the gap… DISPLACEMENT CURRENT 7 Induction - Fall 2006 11 -11 -06

11 -11 -06 Induction - Fall 2006 8

11 -11 -06 Induction - Fall 2006 9

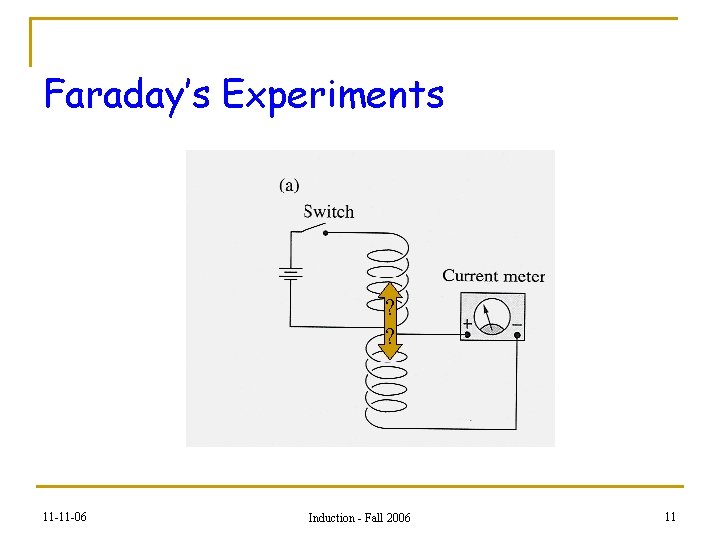
From The Demo. . 11 -11 -06 Induction - Fall 2006 10

Faraday’s Experiments ? ? 11 -11 -06 Induction - Fall 2006 11

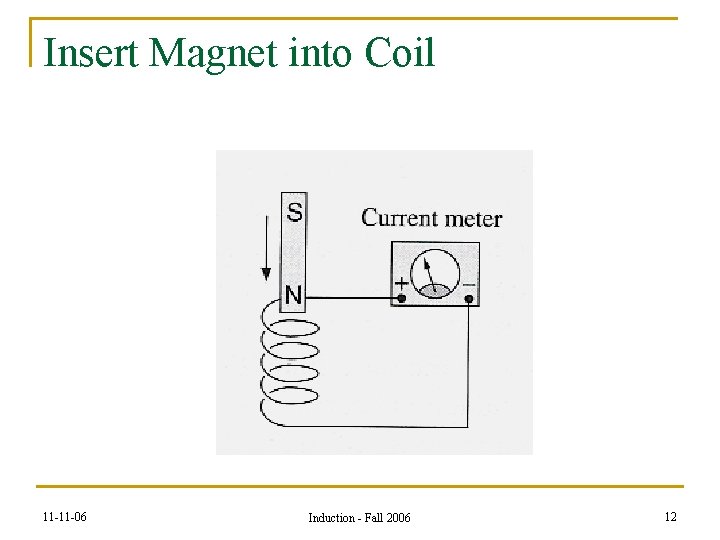
Insert Magnet into Coil 11 -11 -06 Induction - Fall 2006 12

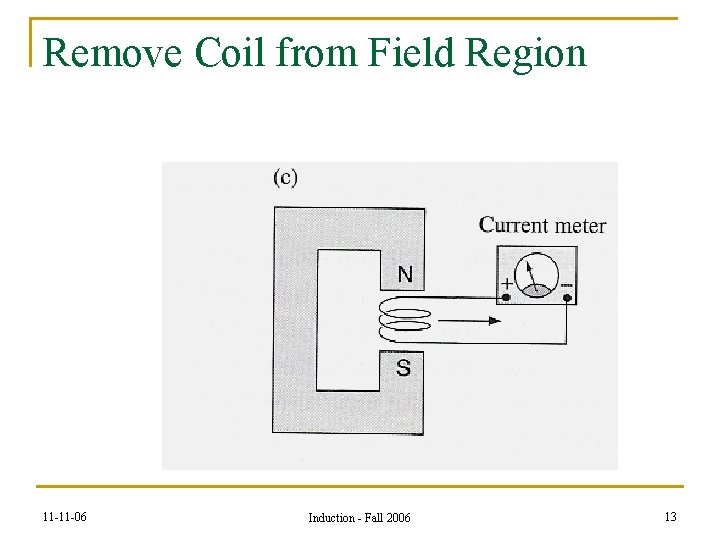
Remove Coil from Field Region 11 -11 -06 Induction - Fall 2006 13

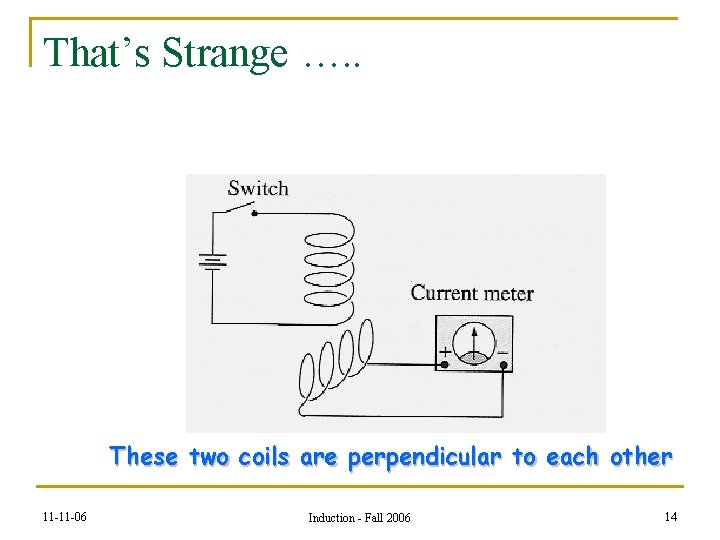
That’s Strange …. . These two coils are perpendicular to each other 11 -11 -06 Induction - Fall 2006 14

Remember the Definition of TOTAL ELECTRIC FLUX through a CLOSED surface: 11 -11 -06 Induction - Fall 2006 15

Magnetic Flux: FB n Similar Definition with a special difference! 11 -11 -06 Induction - Fall 2006 16

Magnetic Flux n n Applies to an OPEN SURFACE only. “Quantity” of magnetism that goes through a surface 11 -11 -06 Induction - Fall 2006 17

Consider a Loop n xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx 11 -11 -06 n n Magnetic field passing through the loop is CHANGING. FLUX is changing. There must be an emf developed around the loop. q n A current develops (as we saw in demo) Work has to be done to move a charge completely around the loop. Induction - Fall 2006 18

Faraday’s Law (Michael Faraday) n xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx 11 -11 -06 n n Again, for a current to flow around the circuit, there must be an emf. (An emf is a voltage) The voltage is found to increase as the rate of change of flux increases. Induction - Fall 2006 19

Faraday’s Law (Michael Faraday) xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx We will get to the minus sign in a short time. 11 -11 -06 Induction - Fall 2006 20

Faraday’s Law (The Minus Sign) xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx 11 -11 -06 Using the right hand rule, we would expect the direction of the current to be in the direction of the arrow shown. Induction - Fall 2006 21

Faraday’s Law (More on the Minus Sign) xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx The minus sign means that the current goes the other way. This current will produce a magnetic field that would be coming OUT of the page. The Induced Current therefore creates a magnetic field that OPPOSES the attempt to INCREASE the magnetic field! This is referred to as Lenz’s Law. 11 -11 -06 Induction - Fall 2006 22

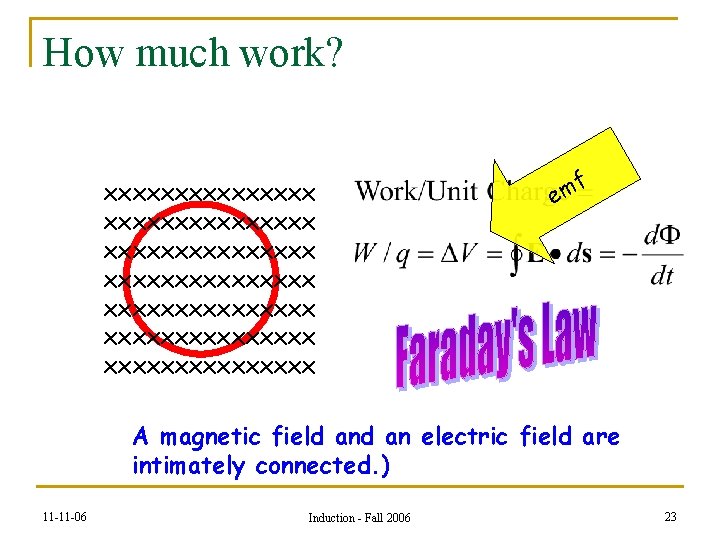
How much work? xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx f m e A magnetic field an electric field are intimately connected. ) 11 -11 -06 Induction - Fall 2006 23

The Strange World of Dr. Lentz 11 -11 -06 Induction - Fall 2006 24

MAGNETIC FLUX n This is an integral over an OPEN Surface. Magnetic Flux is a Scalar n The UNIT of FLUX is the n q 11 -11 -06 weber 1 weber = 1 T-m 2 Induction - Fall 2006 25

We finally stated FARADAY’s LAW 11 -11 -06 Induction - Fall 2006 26

From the equation 11 -11 -06 Induction - Fall 2006 Lentz 27

Flux Can Change n n 11 -11 -06 If B changes If the AREA of the loop changes Changes cause emf s and currents and consequently there are connections between E and B fields These are expressed in Maxwells Equations Induction - Fall 2006 28

Three of Maxwell’s Four Equations (Next Course. . Just a Preview!) Ampere’s Law Gauss Faraday 11 -11 -06 Induction - Fall 2006 29

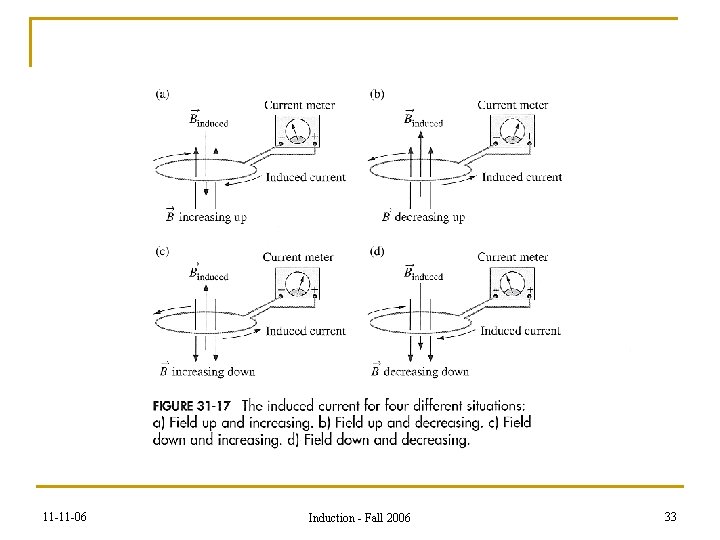
Another View Of That damned minus sign again …. . SUPPOSE that B begins to INCREASE its MAGNITUDE INTO THE PAGE xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx n n n 11 -11 -06 The Flux into the page begins to increase. An emf is induced around a loop A current will flow That current will create a new magnetic field. THAT new field will change the magnetic flux. Induction - Fall 2006 30

Lenz’s Law Induced Magnetic Fields always FIGHT to stop what you are trying to do! i. e. . . Murphy’s Law for Magnets 11 -11 -06 Induction - Fall 2006 31

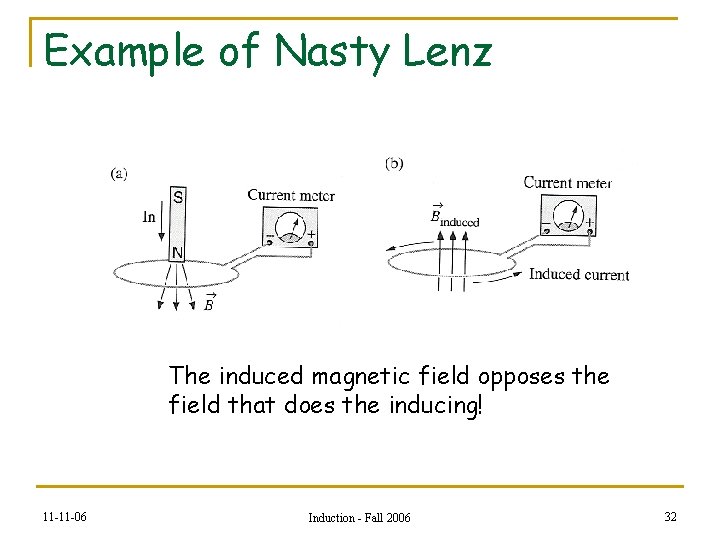
Example of Nasty Lenz The induced magnetic field opposes the field that does the inducing! 11 -11 -06 Induction - Fall 2006 32

11 -11 -06 Induction - Fall 2006 33

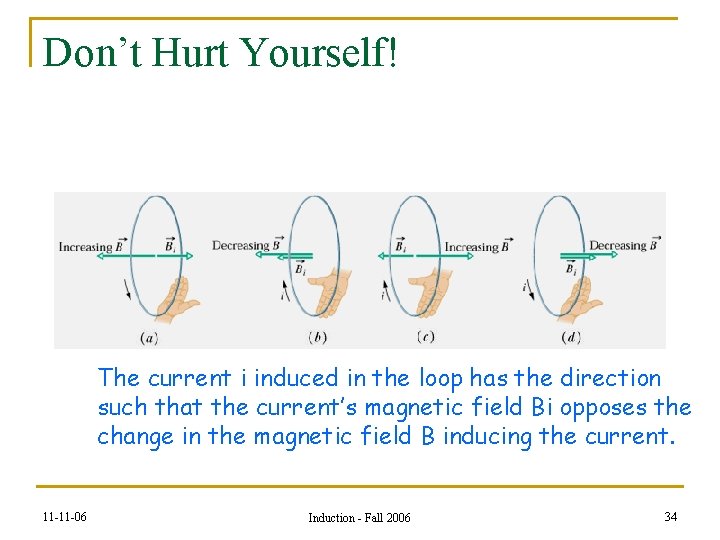
Don’t Hurt Yourself! The current i induced in the loop has the direction such that the current’s magnetic field Bi opposes the change in the magnetic field B inducing the current. 11 -11 -06 Induction - Fall 2006 34

Let’s do the Lentz Warp again ! 11 -11 -06 Induction - Fall 2006 35

Lenz’s Law An induced current has a direction such that the magnetic field due to the current opposes the change in the magnetic flux that induces the current. (The result of the negative sign!) … OR The toast will always fall buttered side down! 11 -11 -06 Induction - Fall 2006 36

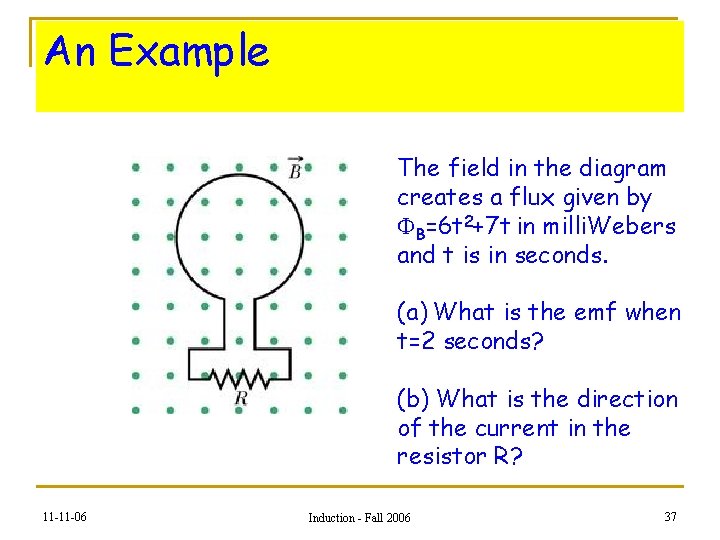
An Example The field in the diagram creates a flux given by FB=6 t 2+7 t in milli. Webers and t is in seconds. (a) What is the emf when t=2 seconds? (b) What is the direction of the current in the resistor R? 11 -11 -06 Induction - Fall 2006 37

This is an easy one … Direction? B is out of the screen and increasing. Current will produce a field INTO the paper (LENZ). Therefore current goes clockwise and R to left in the resistor. 11 -11 -06 Induction - Fall 2006 38

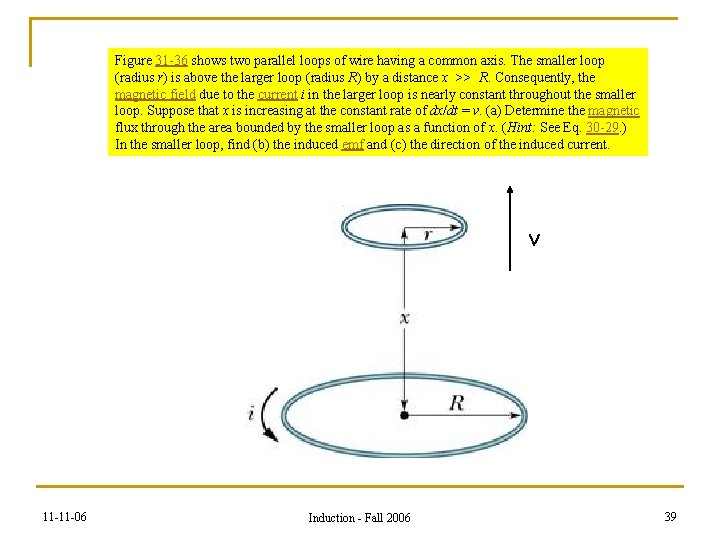
Figure 31 -36 shows two parallel loops of wire having a common axis. The smaller loop (radius r) is above the larger loop (radius R) by a distance x >> R. Consequently, the magnetic field due to the current i in the larger loop is nearly constant throughout the smaller loop. Suppose that x is increasing at the constant rate of dx/dt = v. (a) Determine the magnetic flux through the area bounded by the smaller loop as a function of x. (Hint: See Eq. 30 -29. ) In the smaller loop, find (b) the induced emf and (c) the direction of the induced current. v 11 -11 -06 Induction - Fall 2006 39

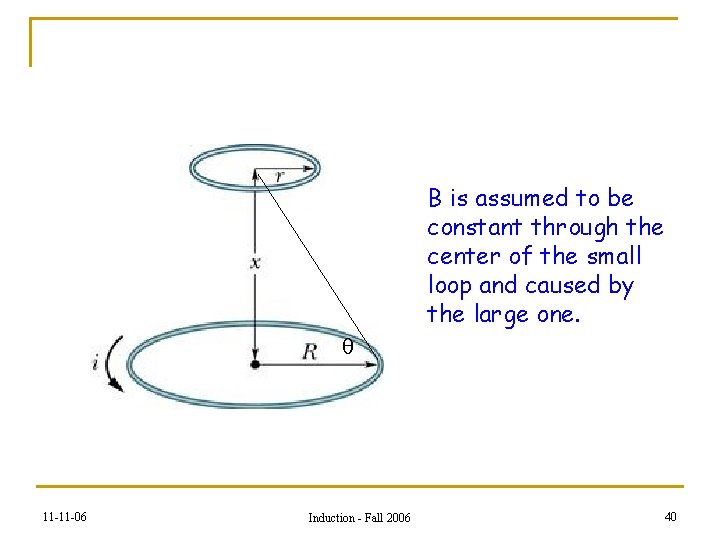
B is assumed to be constant through the center of the small loop and caused by the large one. q 11 -11 -06 Induction - Fall 2006 40

The calculation of Bz q 11 -11 -06 Induction - Fall 2006 41

More Work In the small loop: dx/dt=v 11 -11 -06 Induction - Fall 2006 42

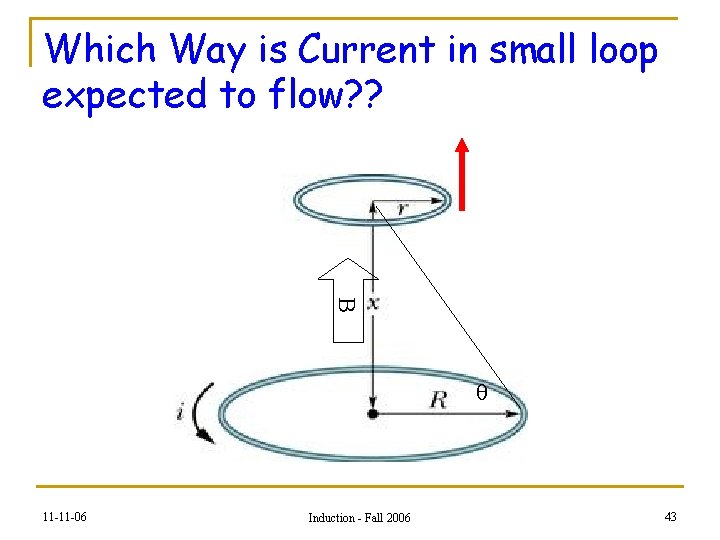
Which Way is Current in small loop expected to flow? ? B q 11 -11 -06 Induction - Fall 2006 43

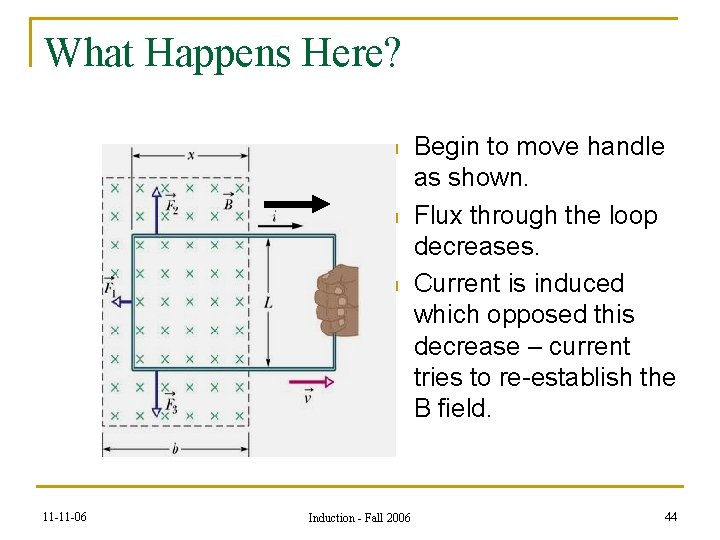
What Happens Here? n n n 11 -11 -06 Induction - Fall 2006 Begin to move handle as shown. Flux through the loop decreases. Current is induced which opposed this decrease – current tries to re-establish the B field. 44

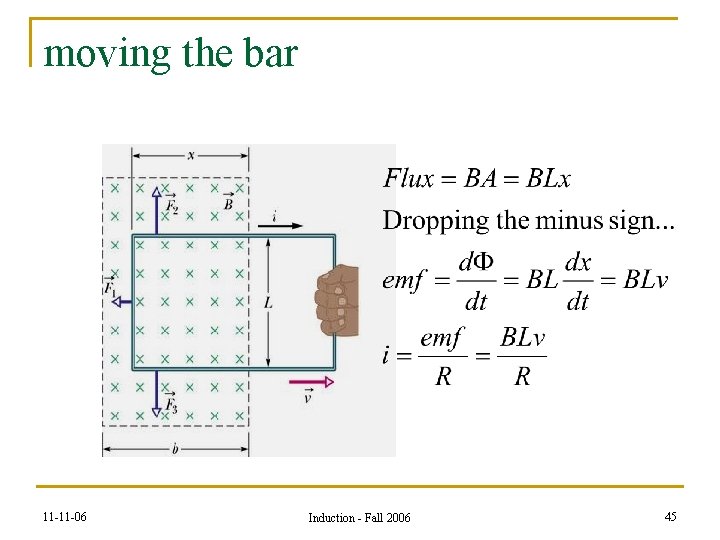
moving the bar 11 -11 -06 Induction - Fall 2006 45

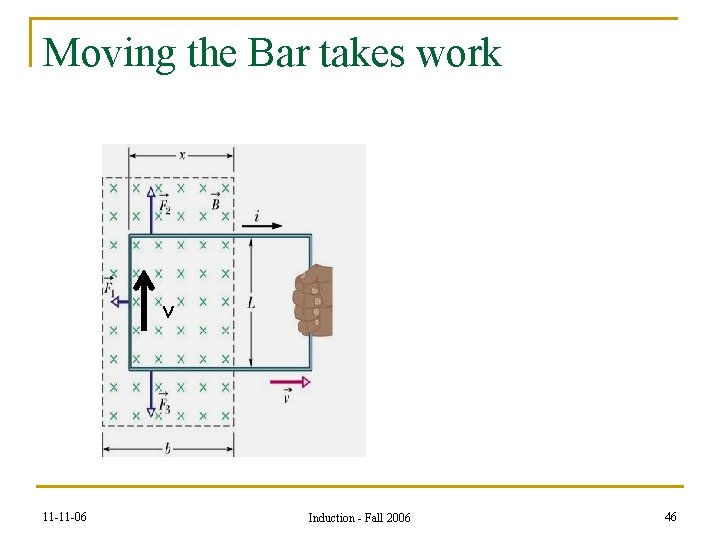
Moving the Bar takes work v 11 -11 -06 Induction - Fall 2006 46

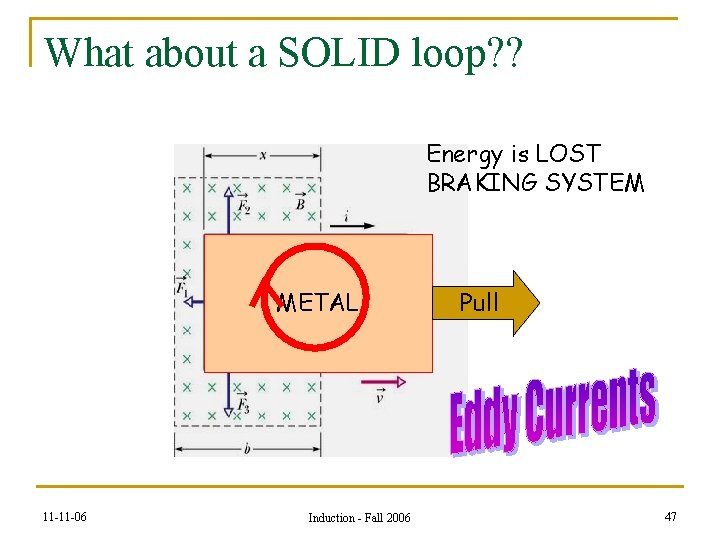
What about a SOLID loop? ? Energy is LOST BRAKING SYSTEM METAL 11 -11 -06 Induction - Fall 2006 Pull 47

Back to Circuits for a bit …. 11 -11 -06 Induction - Fall 2006 48

Definition Current in loop produces a magnetic field in the coil and consequently a magnetic flux. If we attempt to change the current, an emf will be induced in the loops which will tend to oppose the change in current. This this acts like a “resistor” for changes in current! 11 -11 -06 Induction - Fall 2006 49

Remember Faraday’s Law Lentz 11 -11 -06 Induction - Fall 2006 50

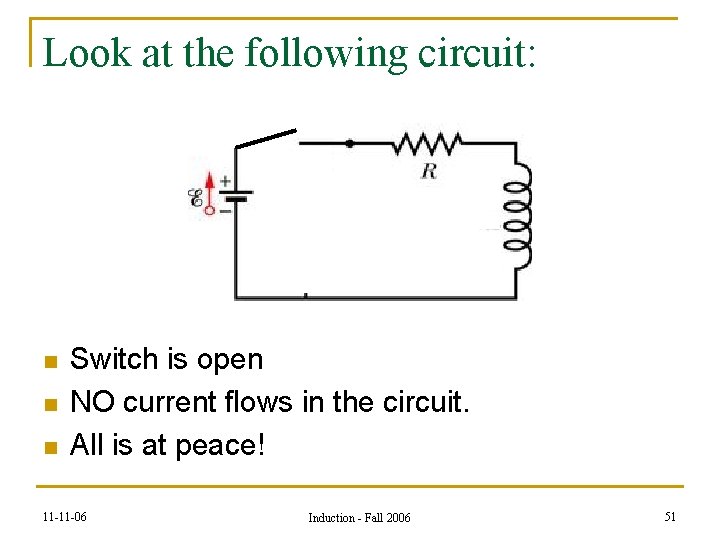
Look at the following circuit: n n n Switch is open NO current flows in the circuit. All is at peace! 11 -11 -06 Induction - Fall 2006 51

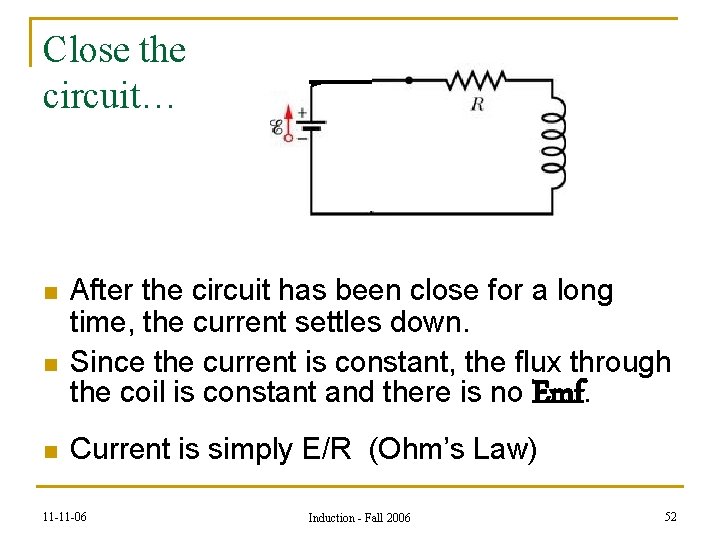
Close the circuit… n n n After the circuit has been close for a long time, the current settles down. Since the current is constant, the flux through the coil is constant and there is no Emf. Current is simply E/R (Ohm’s Law) 11 -11 -06 Induction - Fall 2006 52

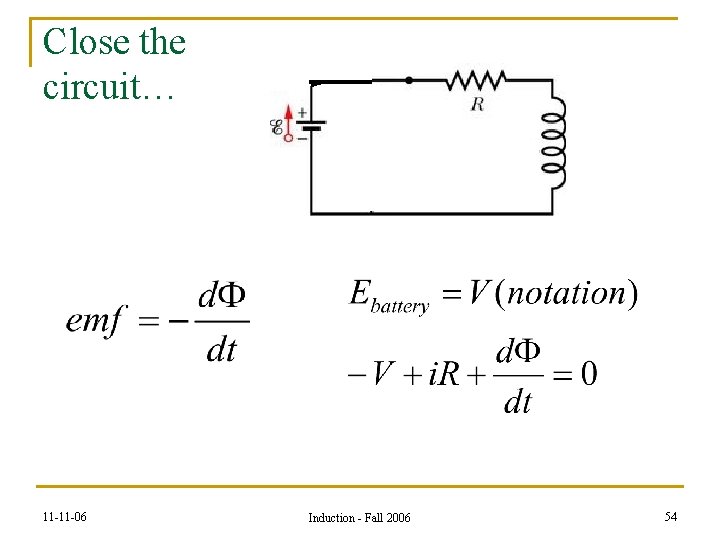
Close the circuit… n n When switch is first closed, current begins to flow rapidly. The flux through the inductor changes rapidly. An emf is created in the coil that opposes the increase in current. The net potential difference across the resistor is the battery emf opposed by the emf of the coil. 11 -11 -06 Induction - Fall 2006 53

Close the circuit… 11 -11 -06 Induction - Fall 2006 54

Moving right along … 11 -11 -06 Induction - Fall 2006 55

Definition of Inductance L UNIT of Inductance = 1 henry = 1 T- m 2/A FB is the flux near the center of one of the coils making the inductor 11 -11 -06 Induction - Fall 2006 56

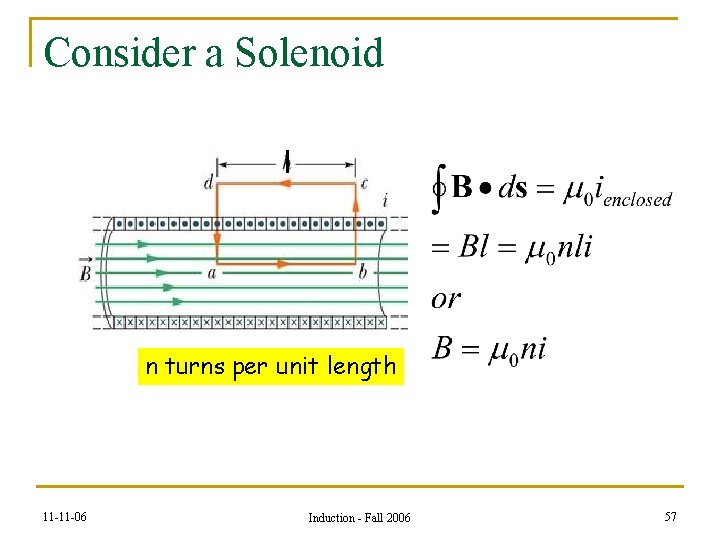
Consider a Solenoid l n turns per unit length 11 -11 -06 Induction - Fall 2006 57

So…. Depends only on geometry just like C and is independent of current. 11 -11 -06 Induction - Fall 2006 58

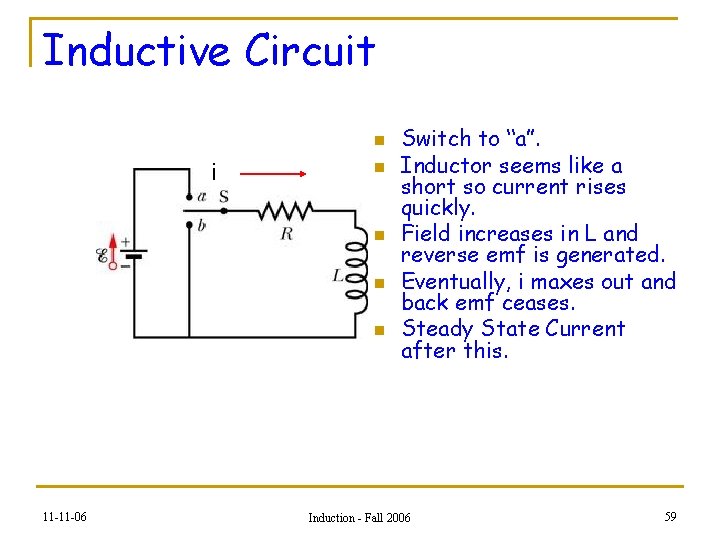
Inductive Circuit n i n n 11 -11 -06 Switch to “a”. Inductor seems like a short so current rises quickly. Field increases in L and reverse emf is generated. Eventually, i maxes out and back emf ceases. Steady State Current after this. Induction - Fall 2006 59

THE BIG INDUCTION n n As we begin to increase the current in the coil The current in the first coil produces a magnetic field in the second coil Which tries to create a current which will reduce the field it is experiences And so resists the increase in current. 11 -11 -06 Induction - Fall 2006 60

Back to the real world… Switch to “a” i 11 -11 -06 Induction - Fall 2006 61

Solution 11 -11 -06 Induction - Fall 2006 62

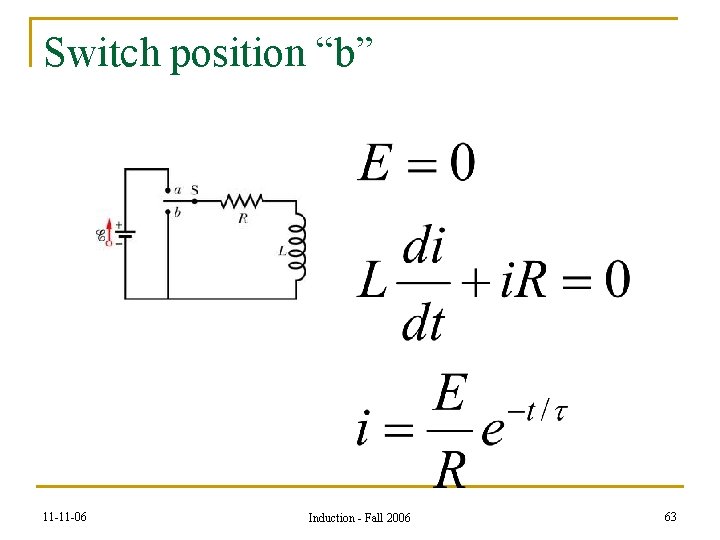
Switch position “b” 11 -11 -06 Induction - Fall 2006 63

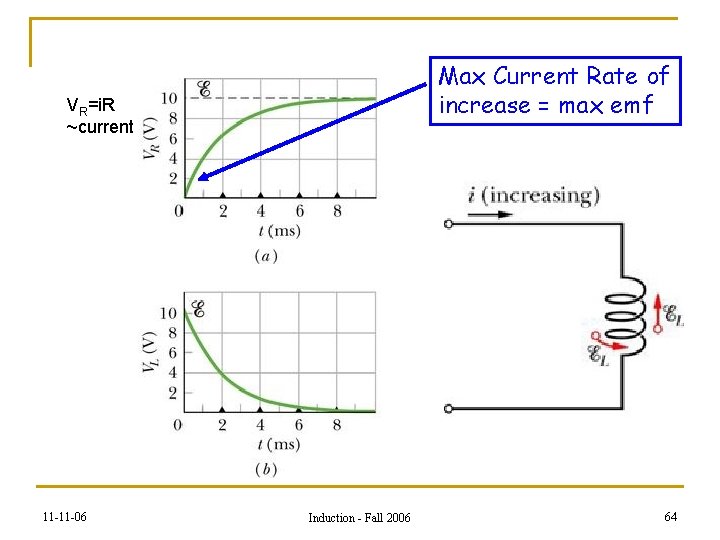
Max Current Rate of increase = max emf VR=i. R ~current 11 -11 -06 Induction - Fall 2006 64

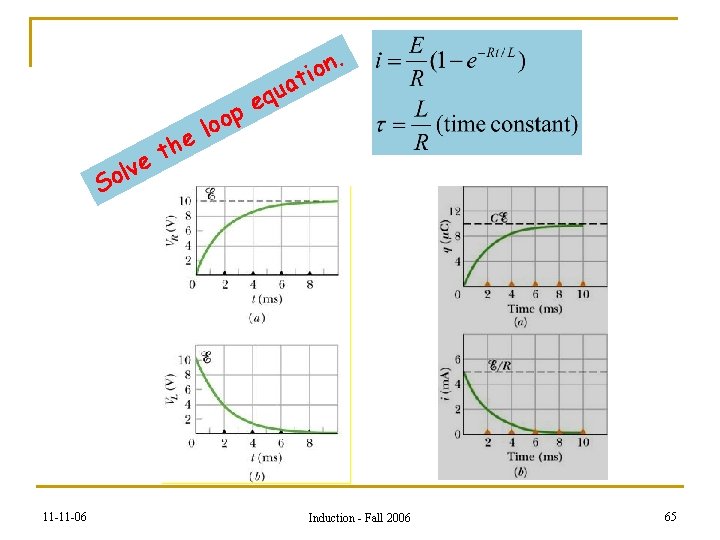
. n o ti he t e v l So 11 -11 -06 p o o l ua q e Induction - Fall 2006 65

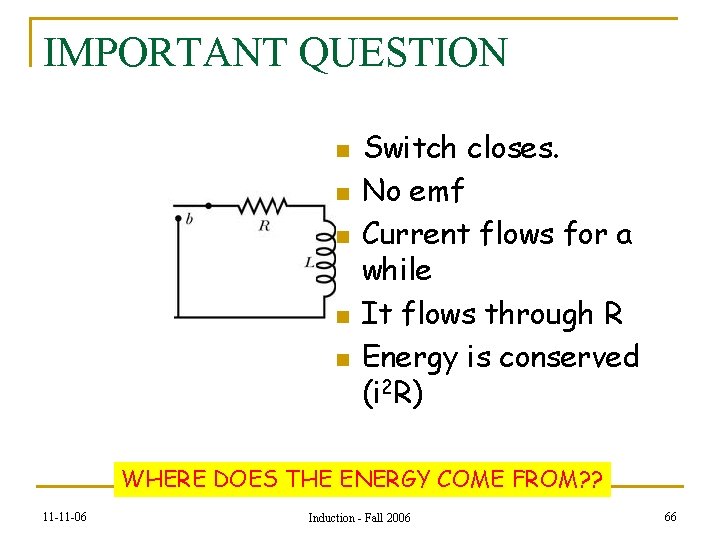
IMPORTANT QUESTION n n n Switch closes. No emf Current flows for a while It flows through R Energy is conserved (i 2 R) WHERE DOES THE ENERGY COME FROM? ? 11 -11 -06 Induction - Fall 2006 66

For an answer Return to the Big C n E=e 0 A/d n n +dq +q 11 -11 -06 -q n We move a charge dq from the (-) plate to the (+) one. The (-) plate becomes more (-) The (+) plate becomes more (+). d. W=Fd=dq x E x d Induction - Fall 2006 67

The calc The energy is in the FIELD !!! 11 -11 -06 Induction - Fall 2006 68

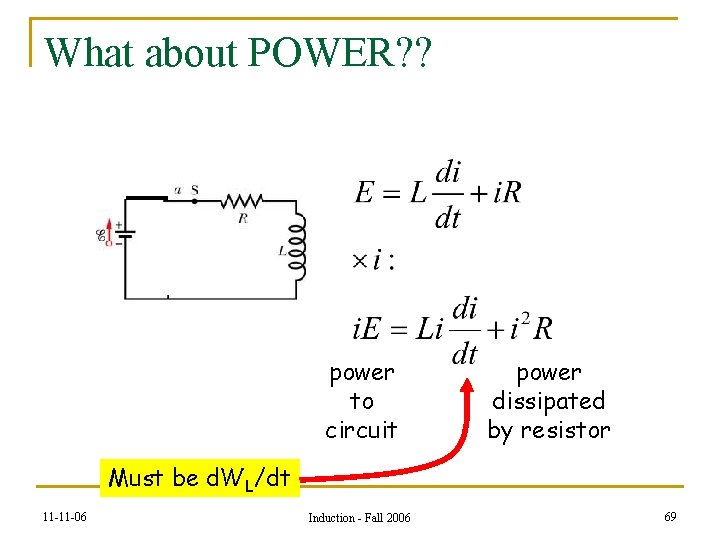
What about POWER? ? power to circuit power dissipated by resistor Must be d. WL/dt 11 -11 -06 Induction - Fall 2006 69
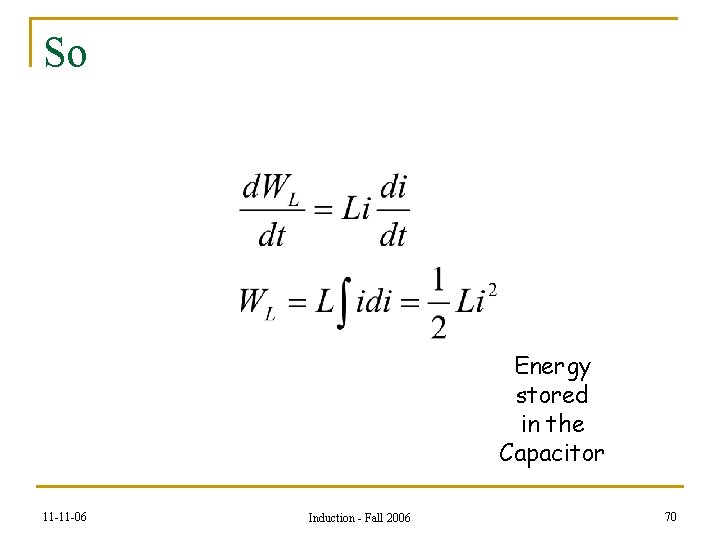
So Energy stored in the Capacitor 11 -11 -06 Induction - Fall 2006 70

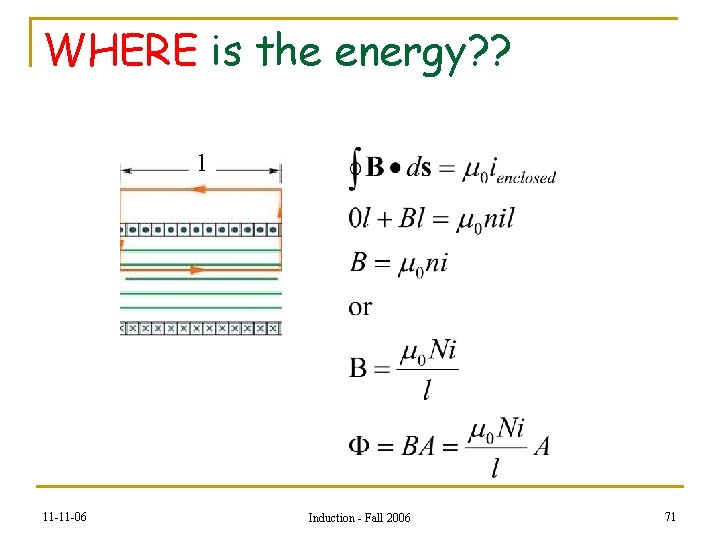
WHERE is the energy? ? l 11 -11 -06 Induction - Fall 2006 71

Remember the Inductor? ? ? ? ? ? ? 11 -11 -06 Induction - Fall 2006 72

So … 11 -11 -06 Induction - Fall 2006 73

ENERGY IN THE FIELD TOO! 11 -11 -06 Induction - Fall 2006 74

IMPORTANT CONCLUSION n n A region of space that contains either a magnetic or an electric field contains electromagnetic energy. The energy density of either is proportional to the square of the field strength. 11 -11 -06 Induction - Fall 2006 75

11 -11 -06 Induction - Fall 2006 76