Induction and Recursion Odd Powers Are Odd Fact

Induction and Recursion

Odd Powers Are Odd Fact: If m is odd and n is odd, then nm is odd. Proposition: for an odd number m, mk is odd for all non-negative integer k. Let P(i) be the proposition that mi is odd. Proof by induction • P(1) is true by definition. • P(2) is true by P(1) and the fact. • P(3) is true by P(2) and the fact. • P(i+1) is true by P(i) and the fact. • So P(i) is true for all i.

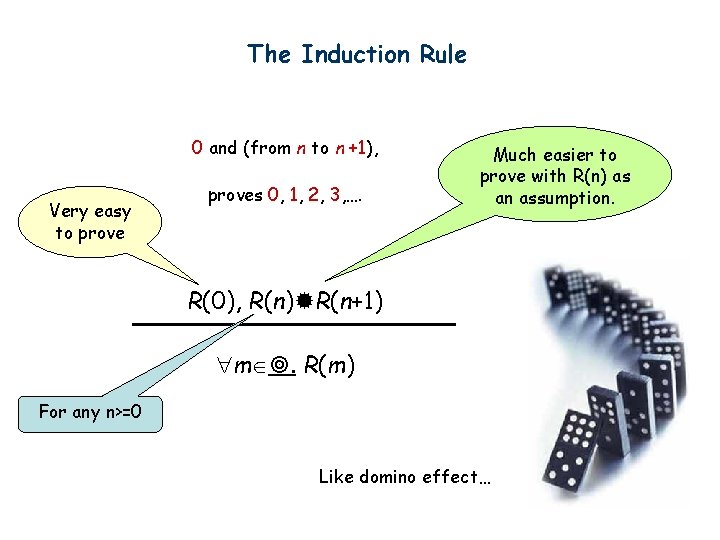
The Induction Rule 0 and (from n to n +1), Very easy to proves 0, 1, 2, 3, …. Much easier to prove with R(n) as an assumption. R(0), R(n) R(n+1) m . R(m) For any n>=0 Like domino effect…

Proof by Induction Let’s prove: Statements in green form a template for inductive proofs. Proof: (by induction on n) The induction hypothesis, P(n), is:

Proof by Induction Base Case (n = 0): Wait: divide by zero bug! This is only true for r 1 Theorem:

Proof by Induction Step: Assume P(n) for some n 0 and prove P(n + 1): Have P (n) by assumption: So let r be any number 1, then from P (n) we have How do we proceed?

Proof by Induction adding r n+1 to both sides, But since r 1 was arbitrary, we conclude (by UG), that which is P (n+1). This completes the induction proof.

Summation Try to prove:

Proving a Property Base Case (n = 1): Induction Step: Assume P(i) for some i 1 and prove P(i + 1):

Proving an Inequality Base Case (n = 3): Induction Step: Assume P(i) for some i 3 and prove P(i + 1):

Strong Induction Strong induction Prove P(0). Then prove P(n+1) assuming all of P(0), P(1), …, P(n) (instead of just P(n)). equivalent Conclude n. P(n) Ordinary induction 0 1, 1 2, 2 3, …, n-1 n. So by the time we got to n+1, already know all of P(0), P(1), …, P(n)

Prime Products Claim: Every integer > 1 is a product of primes. Proof: (by strong induction) Base case is easy. Suppose the claim is true for all 2 <= i < n. Consider an integer n. In particular, n is not prime. So n = k·m for integers k, m where n > k, m >1. Since k, m smaller than n, By the induction hypothesis, both k and m are product of primes k = p 1 p 2 p 94 m = q 1 q 214

Prime Products Claim: Every integer > 1 is a product of primes. …So n = k m = p 1 p 2 p 94 q 1 q 214 is a prime product. This completes the proof of the induction step.

Postage by Strong Induction Available stamps: 5¢ What amount can you form? Theorem: Can form any amount 8¢ Prove by strong induction on n. P(n) : : = can form (n +8)¢. 3¢

Postage by Strong Induction Base case (n = 0): (0 +8)¢: Inductive Step: assume (m +8)¢ for 0 m n, then prove ((n +1) + 8)¢ cases: n +1= 1, 9¢: n +1= 2, 10¢:

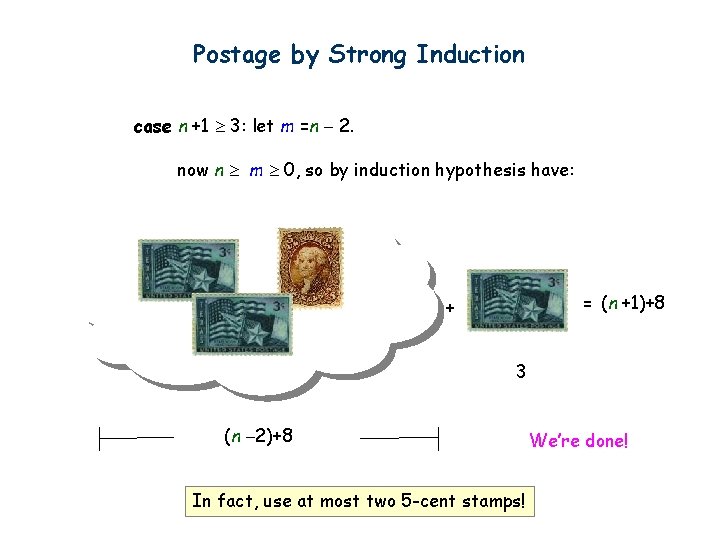
Postage by Strong Induction case n +1 3: let m =n 2. now n m 0, so by induction hypothesis have: = (n +1)+8 + 3 (n 2)+8 In fact, use at most two 5 -cent stamps! We’re done!

Postage by Strong Induction Given an unlimited supply of 5 cent and 7 cent stamps, what postages are possible? Theorem: For all n >= 24, it is possible to produce n cents of postage from 5¢ and 7¢ stamps.

Recursive Definitions and Structural Induction • Sometimes it’s easier to define an object in terms of itself. • This process is called Recursion. • Example: the sequence of powers of 2 is given by a n = 2 n for n = 0, 1, 2, …. This sequence can also be defined by giving the first term of the sequence, namely, a 0 = 1, and a rule finding a term of the sequence from the previous one, namely, an+1 = 2 an, for n = 0, 1, 2, …. 18

Recursively Defined Functions • Use two steps to define a function with the set of nonnegative integers as its domain: BASIS STEP: Specify that value of the function at zero. RECURSIVE STEP: Give a rule for finding its value at an integer from its values at smaller integers. • Such a definition is called a recursive or inductive definition. • Examples: – Suppose that f is defined recursively by f(0) = 3, f(n+1) = 2 f(n) + 3 Find f(1), f(2), f(3), and f(4). Solution: f(1) = 2 f(0) + 3 = 2*3 + 3 = 9 f(2) = 2 f(1) + 3 = 2*9 + 3 = 21 f(3) = 2 f(2) + 3 = 2*21 + 3 = 45 f(4) = 2 f(3) + 3 = 2*45 + 3 = 93 19

Recursive Examples – Give an inductive definition of the factorial function F(n) = n!. Solution: Basis Step: F(0) = 1 Inductive Step: F(n+1) = (n+1)F(n) E. g. Find F(5) = 5 F(4) = 5*4 F(3) = 5*4*3 F(2) = 5 * 4 * 3 * 2 F(1) = 5 * 4 * 3 * 2 * 1 F(0) = 5 * 4 * 3 * 2 * 1 = 120 – Give a recursive definition of . Solution: Basis Step: Inductive Step: 20

Fibonacci Number DEFINITION 1 The Fibonacci numbers, f 0, f 1, f 2, …, are defined by the equations f 0= 0, f 1 = 1, and fn = fn-1 + fn-2 for n = 2, 3, 4, …. • Example: Find the Fibonacci numbers f 2, f 3, f 4, f 5, and f 6. Solution: f 2 = f 1 + f 0 = 1 + 0 = 1, f 3 = f 2 + f 1 = 1 + 1 = 2, f 4 = f 3 + f 2 = 2 + 1 = 3, f 5 = f 4 + f 3 = 3 + 2 = 5, f 6 = f 5 + f 4 + 5 + 3 = 8. • Example: Find the Fibonacci numbers f 7. Solution ? 21

Recursively Defined Sets and Structures DEFINITION 2 The set ∑* of strings over the alphabet ∑ can be defined recursively by BASIS STEP: λ ∑* (where λ is the empty string containing no symbols). RECURSIVE STEP: If w ∑* and x ∑ , then wx ∑*. • The basis step of the recursive definition of strings says that the empty string belongs to ∑*. The recursive step states that new strings are produced by adding a symbol from ∑ to the end of strings in ∑*. At each application of the recursive step, strings containing one additional symbol are generated. • Example: If ∑ = {0, 1}, the strings found to be in ∑*, the set of all bit strings are λ, specified to be in ∑* in the basis step, 0 and 1 formed during the first application of the recursive step, 00, 01, 10, and 11 formed during the second application of the recursive step, and so on. 22

Well-Formed Formulae for Compound Statement Forms. We can define the set of well-formed formulae for compound statement forms involving T, F, propositional variables, and operators from the set {¬, Λ, V, →, ↔}. BASIS STEP: T, F, and s, where s is a propositional variable, are well-formed formulae. RECURSIVE STEP: If E and F are well-formed formulae, then (¬E), (E Λ F), (E V F), (E → F), and (E ↔ F) are well-formed formulae. By the basis step we know that T, F, p, and q are well-formed formulae, where p and q are propositional variables. From an initial application of the recursive step, we know that (p V q), (p → F), (F → q), and (q Λ F) are well-formed formulae. A second application of the recursive step shows that ((p V q) → (q Λ F)), (q V (p V q)), and ((p → F) → T) are well-formed formulae. 23

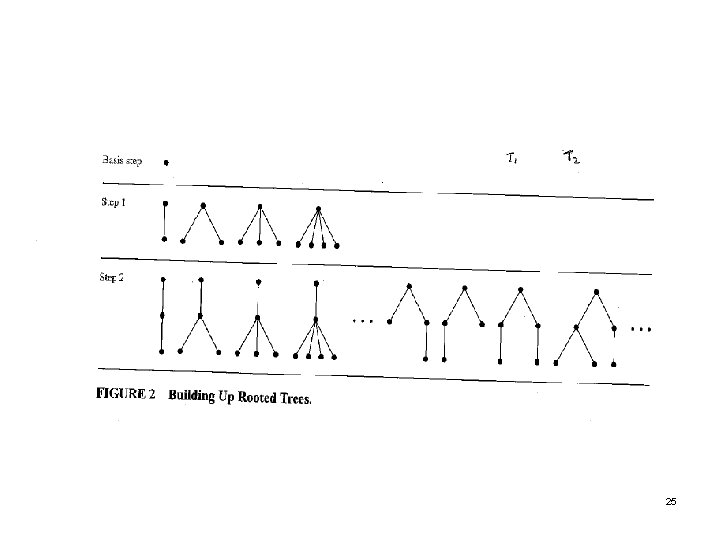
Rooted Tree DEFINITION 4 The set of rooted trees, where a rooted tree consists of a set of vertices containing a distinguished vertex called the root, and edges connecting these vertices, can be defined recursively by these steps: BASIS STEP: A single vertex r is a rooted tree. RECURSIVE STEP: Suppose that T 1, T 2, …, Tn are disjoint rooted trees with roots r 1, r 2, …, rn, respectively. Then the graph formed by starting with a root r, which is not in any of the rooted trees, T 1, T 2, …, Tn, and adding an edge from r to each of the vertices r 1, r 2, . . , rn, is also a rooted tree. 24

25

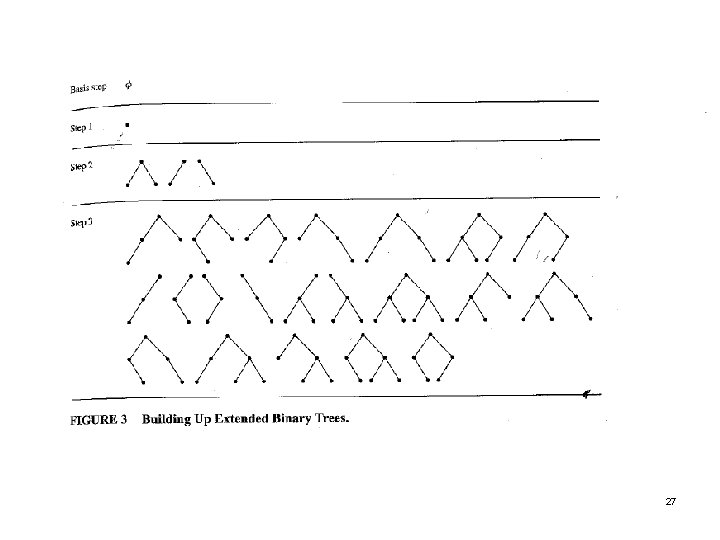
Extended Binary Tree DEFINITION 5 The set of extended binary trees can be defined recursively by these steps: BASIS STEP: The empty set is an extended binary tree. RECURSIVE STEP: If. T 1 and T 2 are disjoint extended binary trees, there is an extended binary tree, denoted by T 1 ·T 2 , consisting of a root r together with edges connecting the root to each of the roots of the left subtree T 1 and the right subtree T 2 when these trees are nonempty. 26

27

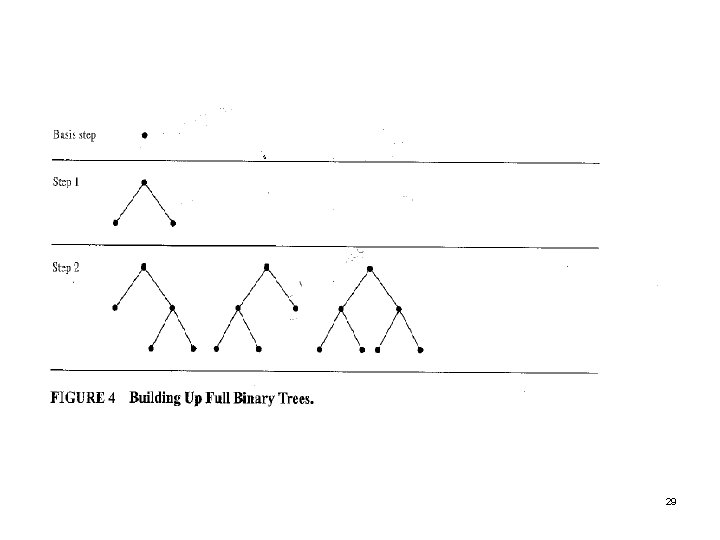
Full Binary Tree DEFINITION 6 The set of full binary trees can be defined recursively by these steps: BASIS STEP: There is a full binary tree consisting only of a single vertex r. RECURSIVE STEP: If. T 1 and T 2 are disjoint full binary trees, there is full binary tree, denoted by T 1 ·T 2 , consisting of a root r together with edges connecting the root to each of the roots of the left subtree T 1 and the right subtree T 2. 28

29

Recursive Algorithms DEFINITION 1 An algorithm is called recursive if it solves a problem by reducing it to an instance of the same problem with smaller input. • Example: Give a recursive algorithm for computer n!, when n is a nonnegative integer. Basis Step: F(0) = 1 Inductive Step: F(n+1) = (n+1)F(n) E. g. Find F(5) = 5 F(4) = 5*4 F(3) = 5*4*3 F(2) = 5 * 4 * 3 * 2 F(1) = 5 * 4 * 3 * 2 * 1 F(0) = 5 * 4 * 3 * 2 * 1 = 120 ALGORITHM 1 A Recursive Algorithm for Computing n!. procedure factorial(n: nonnegative integer) if n = 0 then factorial(n): =1 else factorial(n): =n*factorial(n-1) 30

Recursive Algorithms • Example: Give a recursive algorithm for computer an, where a is a nonzero number and n is a nonnegative integer ALGORITHM 2 A Recursive Algorithm for Computing an. procedure power(a: nonzero real number, n: nonnegative integer) if n = 0 then power(a, n): =1 else power(a, n): =a*power(a, n-1) 31

Linear Search • Example: Express the linear search algorithm as a recursive procedure. ALGORITHM 5 A Recursive Linear Search Algorithm. procedure search(i, j, x: i, j, x integers, 1 <=i<=n, 1<=j<=n) if ai = x then location : = i else if i = j then location : = 0 else search(i+1, j, x) 32

Binary Search • Example: Construct a recursive version of a binary search algorithm ALGORITHM 6 A Recursive Binary Search Algorithm. procedure binary. Search(i, j, x: i, j, x integers, 1 <= i <= n, 1<= j <= n) m : = if x = am then location : = m else if (x < am and i < m ) then binary. Search(x, i, m-1) else if (x > am and j > m ) then binary. Search(x, m+1, j) else location : = 0 33

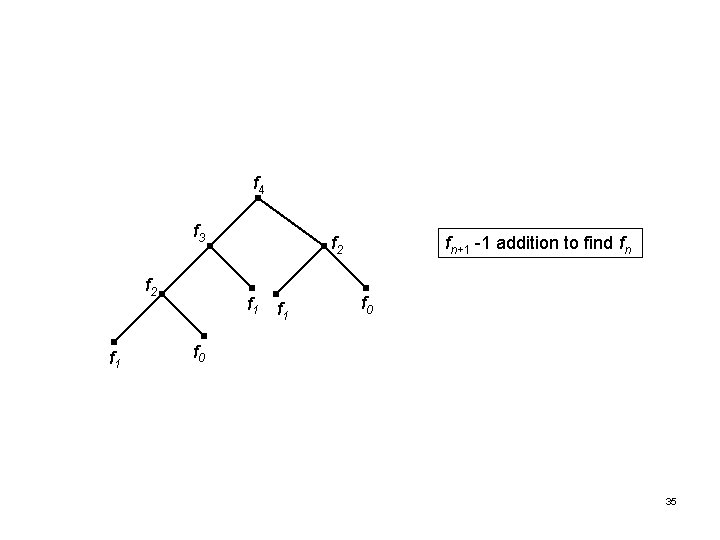
Recursion and Iteration • Sometimes we start with the value of the computation at one or more integers, the base cases, and successively apply the recursive definition to find the values of the function at successive larger integers. Such a procedure is called iterative. ALGORITHM 7 A Recursive Algorithm for Fibonacci Numbers. procedure fibonacci(n: nonnegative integer) if n = 0 then fibonacci(0) : = 0 else if (n = 1) then fibonacci(1) : = 1 else fibonacci(n) : = fibonacci(n-1) + fibonacci(n-2) • How many additions are performed to find fibonacci(n)? 34

f 4 f 3 f 2 f 1 f 1 fn+1 -1 addition to find fn f 0 35

ALGORITHM 8 An Iterative Algorithm for Computing Fibonacci Numbers. procedure iterative. Fibonacci(n: nonnegative integer) if n = 0 then y: = 0 else begin x : = 0 y : = 1 for i : = 1 to n -1 begin z : = x + y x: =y y: =z end {y is the nth Fibonacci number} n – 1 additions are used for an iterative algorithm. 36

Tradeoff • Recursive algorithm may require far more computation than an iterative one. • Sometimes it’s preferable to use a recursive procedure even if it is less efficient. • Sometimes an iterative approach is preferable. 37