Induction and Recursion 1 4 1 Mathematical Induction

Induction and Recursion 1

4. 1 Mathematical Induction Introduction l Mathematical Induction is used to show that P(n) is true for every positive integer n. l Used only to prove results obtained in some other way. l Example: Suppose we have an infinite ladder, and we want to know whether we can reach every step on the ladder. We know two things 1. We can reach the first rung of the ladder. 2. If we can reach a particular rung of the ladder, then we can reach the next rung. Can we conclude that we can reach every rung? By 1, we can reach the first rung. By 2, we can reach the second rung. Apply 2 again, we can reach the third rung… 2 After 100 uses of 2, we can reach the 101 st rung….

4. 1 Mathematical Induction PRINCIPLE OF MATHEMATICAL INDUCTION To prove that P(n) is true for all positive integers n, where P(n) is a propositional function, we complete two steps. BASIS STEP: We verify that P(1) is true. INDUCTIVE STEP: We show that the conditional statement P(k) →P(k+1) is true for all positive integers k. l To complete the inductive step of a proof using the principle of mathematical induction, we assume that P(k) is true for an arbitrary positive integer k and show that under this assumption, P(k+1) must also be true. l The assumption that P(k) is true is called the inductive hypothesis. l The proof technique is stated as [P(1)Λ k(P(k) →P(k+1) )] → n. P(n) where the domain is the set of positive integers 3

4. 1 Mathematical Induction Examples of Proofs by Mathematical Induction l Show that if n is a positive integer, then Solution: BASIS STEP: P(1) is true, because 1 = INDUCTIVE STEP: For the inductive hypothesis we assume that P(k) holds for an arbitrary positive integer k. That is, we assume that Under this assumption, it must be shown that P(k+1) is true, i. e. : When we add k+1 to both sides of the equation in P(k), we obtain This shows that P(k+1) is true under the assumption that P(k) is true. 4 This complete the inductive step.

4. 1 Mathematical Induction l Use mathematical induction to prove that n 3 – n is divisible by 3 whenever n is a positive integer. Solution: BASIS STEP: The statement P(1) is true because 13 – 1 = 0 is divisible by 3. INDUCTIVE STEP: For the inductive hypothesis we assume that P(k) is true; that is we assume that k 3 – k is divisible by 3. To complete the inductive step, we must show that when we assume the inductive hypothesis, the statement (k+1)3 – (k+1) is also divisible by 3. (k+1)3 – (k+1) = (k 3 + 3 k 2 + 3 k + 1) – (k + 1) = (k 3 – k) + 3(k 2 + k) By inductive hypothesis, we know that (k 3 – k) is divisible by 3; and the second term is also divisible by 3. This completes the inductive step. 5

4. 3 Recursive Definitions and Structural Induction Introduction 6

4. 3 Recursive Definitions and Structural Induction l Sometimes it’s easier to define an object in terms of itself. l This process is called Recursion. l Example: The sequence of powers of 2 is given by an = 2 n for n = 0, 1, 2, …. This sequence can also be defined by giving the first term of the sequence, namely, a 0 = 1, and a rule finding a term of the sequence from the previous one, namely, an+1 = 2 an, for n = 0, 1, 2, …. 7

4. 3 Recursive Definitions and Structural Induction Recursively Defined Functions l Use two steps to define a function with the set of nonnegative integers as its domain: BASIS STEP: Specify that value of the function at zero. RECURSIVE STEP: Give a rule for finding its value at an integer from its values at smaller integers. l Such a definition is called a recursive or inductive definition. l Examples: ¡ Suppose that f is defined recursively by f(0) = 3, f(n+1) = 2 f(n) + 3 Find f(1), f(2), f(3), and f(4). Solution: f(1) = 2 f(0) + 3 = 2*3 + 3 = 9 f(2) = 2 f(1) + 3 = 2*9 + 3 = 21 f(3) = 2 f(2) + 3 = 2*21 + 3 = 45 f(4) = 2 f(3) + 3 = 2*45 + 3 = 93 8

4. 3 Recursive Definitions and Structural Induction l Examples: ¡ Give an inductive definition of the factorial function F(n) = n!. Solution: Basis Step: F(0) = 1 Inductive Step: F(n+1) = (n+1)F(n) E. g. Find F(5) = 5 F(4) = 5*4 F(3) = 5*4*3 F(2) = 5 * 4 * 3 * 2 F(1) = 5 * 4 * 3 * 2 * 1 F(0) = 5 * 4 * 3 * 2 * 1 = 120 ¡ Give a recursive definition of . Solution: Basis Step: Inductive Step: 9

4. 3 Recursive Definitions and Structural Induction DEFINITION 1 The Fibonacci numbers, f 0, f 1, f 2, …, are defined by the equations f 0= 0, f 1 = 1, and fn = fn-1 + fn-2 for n = 2, 3, 4, …. l Example: Find the Fibonacci numbers f 2, f 3, f 4, f 5, and f 6. Solution: f 2 = f 1 + f 0 = 1 + 0 = 1, f 3 = f 2 + f 1 = 1 + 1 = 2, f 4 = f 3 + f 2 = 2 + 1 = 3, f 5 = f 4 + f 3 = 3 + 2 = 5, f 6 = f 5 + f 4 + 5 + 3 = 8. l Example: Find the Fibonacci numbers f 7. Solution ? 10

4. 4 Recursive Algorithms Introduction DEFINITION 1 An algorithm is called recursive if it solves a problem by reducing it to an instance of the same problem with smaller input. l Example: Give a recursive algorithm for computer n!, when n is a nonnegative integer. Review: Basis Step: F(0) = 1 Inductive Step: F(n+1) = (n+1)F(n) E. g. Find F(5) = 5 F(4) = 5*4 F(3) = 5*4*3 F(2) = 5 * 4 * 3 * 2 F(1) = 5 * 4 * 3 * 2 * 1 F(0) = 5 * 4 * 3 * 2 * 1 = 120 ALGORITHM 1 A Recursive Algorithm for Computing n!. procedure factorial(n: nonnegative integer) if n = 0 then factorial(n): =1 else factorial(n): =n*factorial(n-1) 11

4. 4 Recursive Algorithms l Example: Give a recursive algorithm for computer an, where a is a nonzero number and n is a nonnegative integer ALGORITHM 2 A Recursive Algorithm for Computing an. procedure power(a: nonzero real number, n: nonnegative integer) if n = 0 then power(a, n): =1 else power(a, n): =a*power(a, n-1) 12

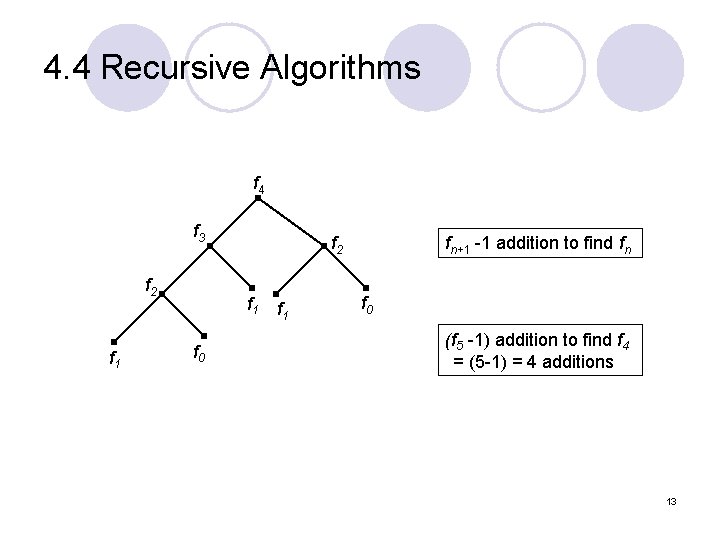
4. 4 Recursive Algorithms f 4 f 3 f 2 f 1 f 0 f 1 fn+1 -1 addition to find fn f 0 (f 5 -1) addition to find f 4 = (5 -1) = 4 additions 13