INDR 262 INTRODUCTION TO OPTIMIZATION METHODS LINEAR ALGEBRA

INDR 262 INTRODUCTION TO OPTIMIZATION METHODS LINEAR ALGEBRA INDR 262 Metin Türkay 1

Matrices • m and n are positive integers • Order of matrix: mxn • The number in the ith row and jth column of A is called the ijth element of A and is written aij. INDR 262 Metin Türkay 2

Example INDR 262 Metin Türkay 3

Equal Matrices • Two matrices A and B are equal if and only if A and B are of the same order and for all i and j, aij=bij. • If A=B, then x=1, y=2, w=3, z=4 INDR 262 Metin Türkay 4

Vectors • A list of n real numbers, say (a 1, a 2, …, an) is called an ndimensional vector. An n-dimensional vector also maybe displayed as a 1 by n matrix. INDR 262 Metin Türkay 5

Scalar Product of Two Vectors • The scalar product of vectors u = [u 1 u 2 … un] and is u 1 v 1+u 2 v 2+…+unvn INDR 262 Metin Türkay 6

Example • uv = 1 x 2+2 x 1+3 x 2 = 10 INDR 262 Metin Türkay 7

Notes • If u = [1 2 3] and , then uv is not defined because the vectors are of different dimensions. • Two vectors are perpendicular to each other if and only if their scalar product is equal to 0. • E. g. , u = [1 -1] and . INDR 262 Metin Türkay 8

Scalar Multiple of a Matrix • Given any matrix A and any scalar c, the scalar multiple of matrix A, c. A, is obtained from the matrix A by multiplying each element of A by c. INDR 262 Metin Türkay 9

Addition of two Matrices • Let A=[aij] and B=[bij] be two matrices with the same order (say mxn). Then, the matrix C=A+B is defined to be the mxn matrix whose ijth element is aij+bij. INDR 262 Metin Türkay 10

The Transpose of a Matrix • Given any mxn matrix the transpose of A (written AT) is the nxm matrix INDR 262 Metin Türkay 11

Example • For any matrix A, (AT)T=A. INDR 262 Metin Türkay 12

Matrix Multiplication • Given two matrices A and B, the matrix product of A and B is defined if and only if the number of columns in A is equal to the number of rows in B. The matrix product C=AB is determined as follows: cij = scalar product of (row i of A and column j of B) INDR 262 Metin Türkay 13

Properties of Matrix Multiplication 1. Matrix multiplication is associative, i. e. , A(BC)=(AB)C. 2. Matrix multiplication is distributive, i. e. , A(B+C)=AB+AC. INDR 262 Metin Türkay 14

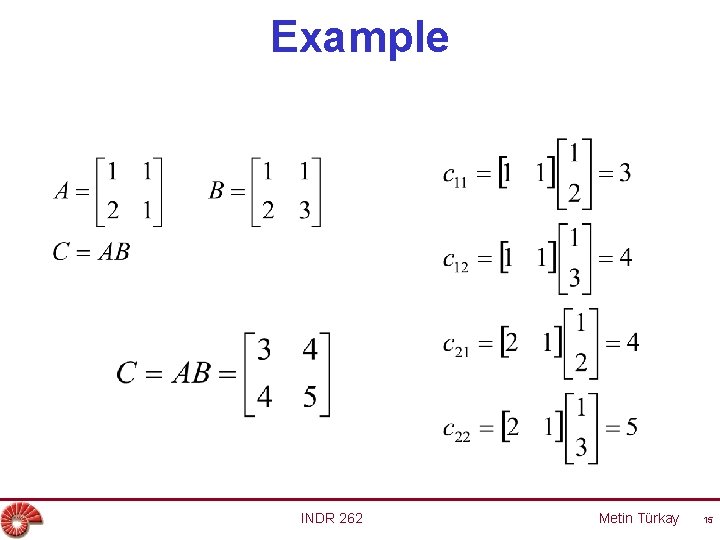
Example INDR 262 Metin Türkay 15

Matrices and Systems of Linear Equations • Consider a system of linear equations given by • x 1, x 2, …, xn are referred to as variables • aij’s and bi’s are constants • A set of equations like above is called a linear system of m equations in n variables INDR 262 Metin Türkay 16

Solution • A solution to a linear system of m equations in n unknowns is a set of values for the unknowns that satisfy each of the systems m equations. INDR 262 Metin Türkay 17

Example x 1 + 2 x 2 = 5 2 x 1 - x 2 = 0 Solution Not a solution INDR 262 Metin Türkay 18

Matrix Representation of Systems of Linear Equations Ax = b Augmented matrix INDR 262 Metin Türkay 19

The Gauss-Jordan Method for Solving Systems of Linear Equations • Gauss-Jordan method is used to find solution(s) to systems of linear equations. A system of linear equations must satisfy one of the following cases: • Case 1: The system has no solution • Case 2: The system has a unique solution • Case 3: The system has an infinite number of solutions INDR 262 Metin Türkay 20

Elementary Row Operations • An ero transforms a given matrix A into a new matrix A’ via one of the following operations. • Type 1 ero: A’ is obtained by multiplying any row of A by a nonzero scalar. • Type 2 ero: Begin by multiplying any row of A (say, row i) by a nonzero scalar c. For some j i, let row j of A’ = c(row i of A) + row j of A, and let the other rows of A’ be the same as the rows of A. • Type 3 ero: Interchange any two rows of A. INDR 262 Metin Türkay 21

Facts • If the matrix A’ is obtained from A via an ero, A’ and A are equivalent. • If the augmented matrix [A’ b’] is obtained from [A b] via an ero, the systems Ax=b and A’x=b’ are equivalent. • Any sequence of ero’s performed on the augmented matrix [A b] corresponding to the system Ax=b will yield an equivalent linear system. INDR 262 Metin Türkay 22

Gauss-Jordan Method • The Gauss-Jordan method solves a linear system of equations by utilizing ero’s in a systematic fashion. Step 1 To solve Ax=b, write down the augmented matrix [A b]. Step 2 At any stage, define a current row, current column, and a current entry. Begin with row 1 as the current row, column 1 as the current column, and a 11 as the current entry. INDR 262 Metin Türkay 23

Gauss-Jordan Method a If a 11 (the current entry) is nonzero, use ero’s to transform column 1 (the current column) to [1 0 … 0]T. Then, obtain the new current row, column, and entry by moving down one row and one column to the right, and go to Step 3. b If a 11 (the current entry) equals 0, then do a Type 3 ero involving the current row and any row that contains a nonzero entry in the current column. Use ero’s to transform column 1 (the current column) to [1 0 … 0]T. Then, obtain the new current row, column, and entry by moving down one row and one column to the right, and go to Step 3. c If there are no nonzero numbers in the first column, obtain a new current column and entry by moving one column to the right. Then go to Step 3. INDR 262 Metin Türkay 24

Gauss-Jordan Method Step 3 a If the new current entry is nonzero, use ero’s to transform it to 1 and the rest of the current column’s entries to 0. When finished, obtain a new current row, column, and entry. If this is impossible, stop. Otherwise, repeat Step 3. b If the current entry is 0, do a Type 3 ero with the current row and any row that contains a nonzero entry in the current column. Then, use ero’s to transform column entry to 1 and the rest of the current column’s entries to 0. When finished, obtain the new current row, column, and entry. If this is impossible, stop. Otherwise, repeat Step 3. c If the current column has no nonzero numbers below the current row, obtain a new current column and entry and repeat Step 3. If it is impossible, stop. INDR 262 Metin Türkay 25

Gauss-Jordan Method Step 4 Write down the system of equations A’x=b’ that corresponds to the matrix [A’ b’] obtained when Step 3 is completed. Then, A’x=b’ will have the same set of solutions as Ax=b. • The Gauss–Jordan method converts the augmented matrix [A b] into [A’ b’] such that INDR 262 Metin Türkay 26

Example • Solve the following system of linear equations using the Gauss-Jordan method. 2 x 1 + 2 x 2 + x 3 = 9 2 x 1 - x 2 + 2 x 3 = 6 x 1 - x 2 + 2 x 3 = 5 INDR 262 Metin Türkay 27

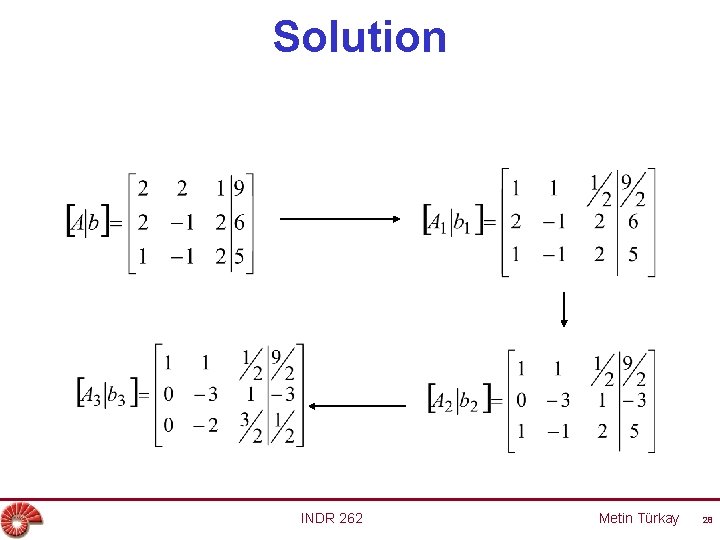
Solution INDR 262 Metin Türkay 28

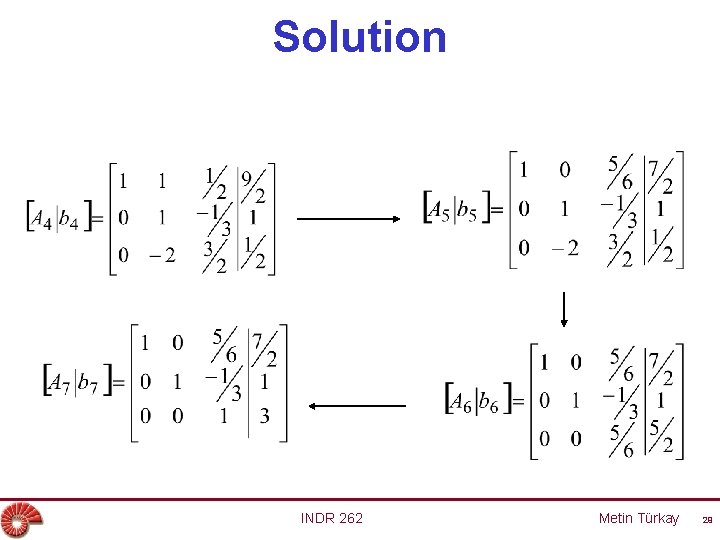
Solution INDR 262 Metin Türkay 29

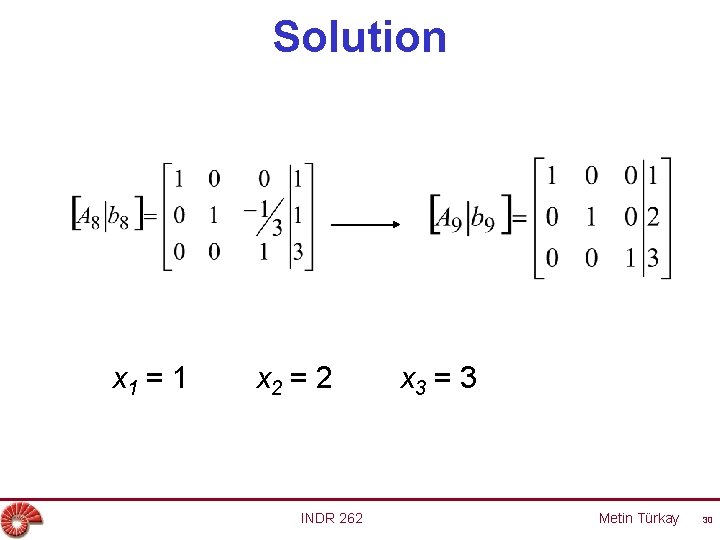
Solution x 1 = 1 x 2 = 2 INDR 262 x 3 = 3 Metin Türkay 30

Analysis of the Solutions to Systems of Linear Equations • For any linear system, a variable that appears with a coefficient of 1 in a single equation and a coefficient of 0 in all other equations is called a basic variable. Any variable that is not a basic variable is called a nonbasic variable. x x. B x. N set of all of the variables in the system Ax=b set of all of the basic variables in the system Ax=b set of all of the nonbasic variables in the system Ax=b x = x. B x. N INDR 262 Metin Türkay 31

Analysis of the Solutions to Systems of Linear Equations • The solution to A’x=b’ can be categorized in one of the three cases: Case 1: A’x=b’ has at least one row of the form [0 0 … 0 c] and c 0. Then, Ax=b has no solution. Case 2: When case 1 does not apply and x. N= , then Ax=b has a unique solution. Case 3: When case 1 does not apply and x. N , then Ax=b has infinite number of solutions. INDR 262 Metin Türkay 32

Example • Case 1 does not apply since there are no rows of the form [0 0 … 0 c] and c 0. • Case 2 does not apply since, x. B={x 1, x 2, x 3} x. N={x 4, x 5} • There are infinite number of solutions. INDR 262 Metin Türkay 33

Example • Assign arbitrary values to the variables in x. N; x 4=c, x 5=k. • Write down the equations in [A’ b’], x 1 + c + k = 3 x 1 = 3 - c – k x 2 + 2 c = 2 x 2 = 2 - 2 c x 3 +k=1 x 3 = 1 - k • It is easy to see that there are infinite number of values of c and k that will satisfy this system of equations. INDR 262 Metin Türkay 34

Linear Combination • A linear combination of the vectors in V is any vector of the form c 1 v 1+c 2 v 2+…+ckvk, where c 1, c 2, …, ck are arbitrary scalars. • Example: V={[1, 2], [2, 1]} 2 v 1 -v 2 = 2([1 2]) – [2 1] = [0 3] 0 v 1 -3 v 2 = 0([1 2]) – 3([2 1]) = [6 3] INDR 262 Metin Türkay 35

Linear Independence & Linear Dependence • A set V of m-dimensional vectors is linearly independent if the only linear combination of vectors in V that equals 0 is the trivial linear combination. • A set V of m-dimensional vectors is linearly dependent if there is a nontrivial linear combination of the vectors in V that adds up to 0. INDR 262 Metin Türkay 36

Example 1 • • V={[1, 0], [0, 1]} Try to find a linear combination of vectors in V that yields 0. c 1([1 0]) + c 2([0 1]) = [0 0] In order to satisfy this, [c 1 c 2] = [0 0] c 1=c 2=0 The only linear combination of vectors in V that yields 0 is the trivial linear combination. Therefore, V is a linearly independent set of vectors. INDR 262 Metin Türkay 37

Example 2 • • V={[1, 2], [2, 4]} Try to find a linear combination of vectors in V that yields 0. c 1([1 2]) + c 2([2 4]) = [0 0] [c 1 2 c 1] + [2 c 2 4 c 2] = [0 0] c 1 + 2 c 2 = 0 c 1 = -2 c 2 2 c 1 + 4 c 2 = 0 2 c 1 = -4 c 2 So, c 1 = 2 c 2 = -1 is one of the possible solutions. There exists a nontrivial linear combination of vectors in V that yields 0. Therefore, V is a linearly dependent set of vectors. INDR 262 Metin Türkay 38

The Rank of a Matrix • Let A be any mxn matrix, and denote the rows of A by r 1, r 2, …, rm. Also define R={ r 1, r 2, …, rm}. • The rank of A is the number of vectors in the largest linearly independent subset of R. • If for a matrix A with m rows, rank A=m; then the matrix is a collection of linearly independent set of vectors. If rank A<m; then the matrix contains a linearly dependent set of vectors. INDR 262 Metin Türkay 39

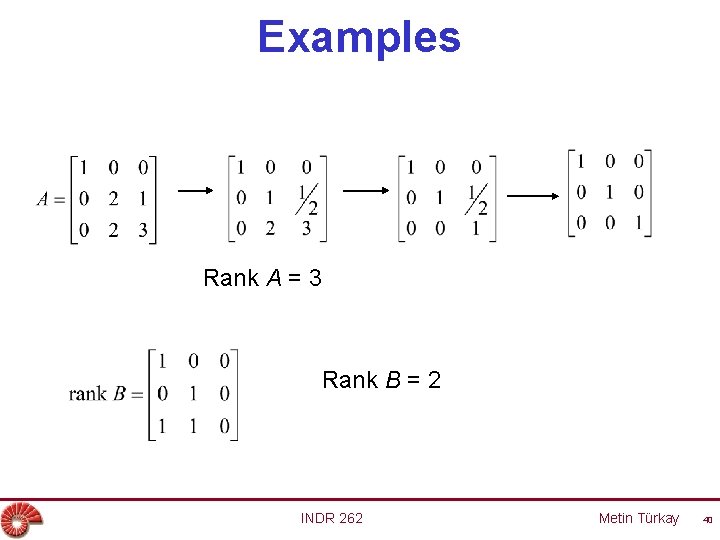
Examples Rank A = 3 Rank B = 2 INDR 262 Metin Türkay 40

The Inverse of a Matrix • A single linear equation in a single variable can be solved by multiplying both sides of the equation by multiplicative inverse of the variable coefficient. • Example: 4 x=3 4 -1(4 x) = (4 -1)3 x=3/4 • We can generalize this approach to square systems of linear equations (i. e. , number of equations = number of unknowns). INDR 262 Metin Türkay 41

Square and Identity Matrix • A square matrix is any matrix that has an equal number of rows and columns. • The diagonal elements of a square matrix are those elements aij such that i=j. • A square matrix for which all diagonal elements are equal to 1 and all non-diagonal elements are equal to 0 is called an identity matrix. INDR 262 Metin Türkay 42

Inverse of A • For a given mxm matrix A, the mxm matrix B is the inverse of A if BA = AB = Im AA-1=I INDR 262 Metin Türkay 43

Finding the Inverse of a Matrix with the Gauss-Jordan Method Step 1 Write down the mx 2 m matrix [A Im]. Step 2 Use ero’s to transform [A Im] into [Im B]. This will only be possible if rank A=m; in this case, B=A-1. If rank A<m, then A has no inverse. INDR 262 Metin Türkay 44

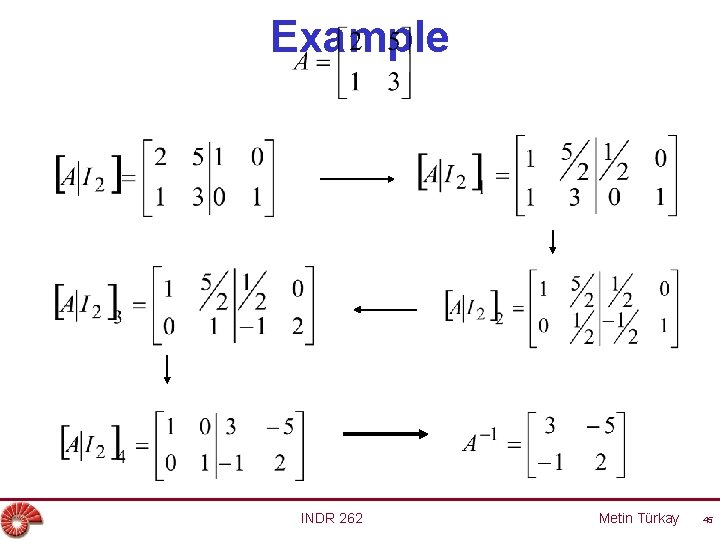
Example INDR 262 Metin Türkay 45

Using Matrix Inverse to Solve Linear Systems of Equations • Given a linear system of equations, Ax=b • Multiply both sides by A-1 AA-1 x = A-1 b INDR 262 Metin Türkay 46

Example 2 x 1 + 5 x 2 = 7 x 1 + 3 x 2 = 4 INDR 262 Metin Türkay 47

Determinant of a Matrix • Any square matrix A has a number called the determinant of A (shown by set A or A ). INDR 262 Metin Türkay 48

Minor of A • If A is an mxm matrix; then for any values of i and j, the ijth minor of A (Aij) is the (m-1)x(m-1) submatrix of A obtained by deleting row i and column j of A. INDR 262 Metin Türkay 49

Determinant of a Matrix • Let A be any mxm matrix, • det A = (-1)i+1 ai 1(det Ai 1) + (-1)i+2 ai 2(det Ai 2) + … +(1)i+maim(det Aim) INDR 262 Metin Türkay 50

Example 1 det A = (-1)1+1 1 det A 11 + (-1)1+2 0 det A 12 + (-1)i+3 1 det Ai 3 INDR 262 Metin Türkay 51

Example 2 det A = -48 INDR 262 Metin Türkay 52