Indistinguishability Obfuscation from Multilinear Maps Huijia Rachel Lin

Indistinguishability Obfuscation from Multilinear Maps Huijia (Rachel) Lin UCSB

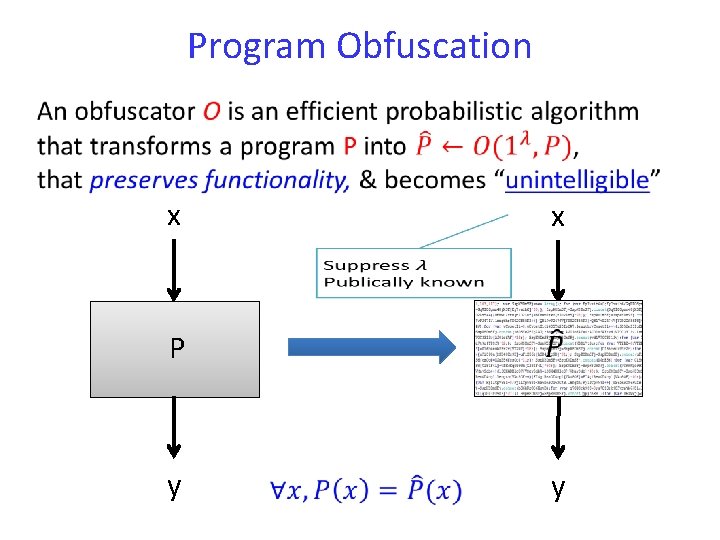
Program Obfuscation x x P y y

Program Obfuscation Different notions of obfuscation Virtual-Black-Box (VBB) [BGI+12, GK, BCC+14] Virtual-Grey-Box (VGB) [BC 10] Differing-input Obfuscation (di. O) [BGI+12] Indistinguishability Obfuscation (i. O) [BGI+12]

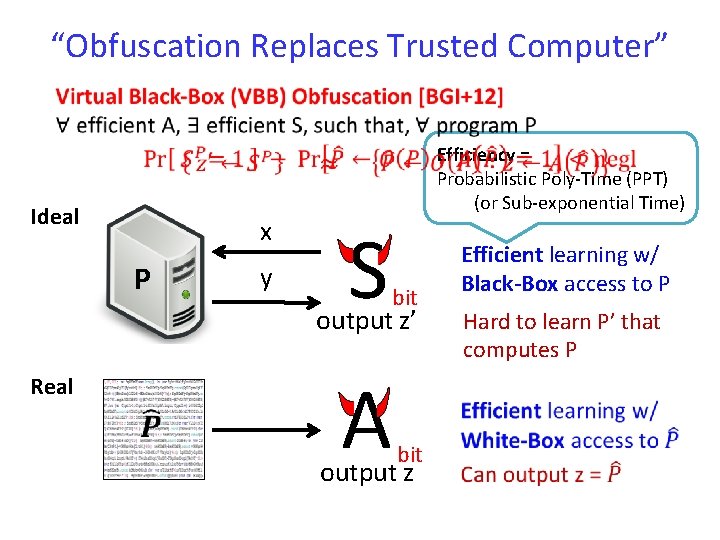
“Obfuscation Replaces Trusted Computer” Ideal x P y Efficiency = Probabilistic Poly-Time (PPT) (or Sub-exponential Time) S bit A bit output z’ Real output z Efficient learning w/ Black-Box access to P Hard to learn P’ that computes P

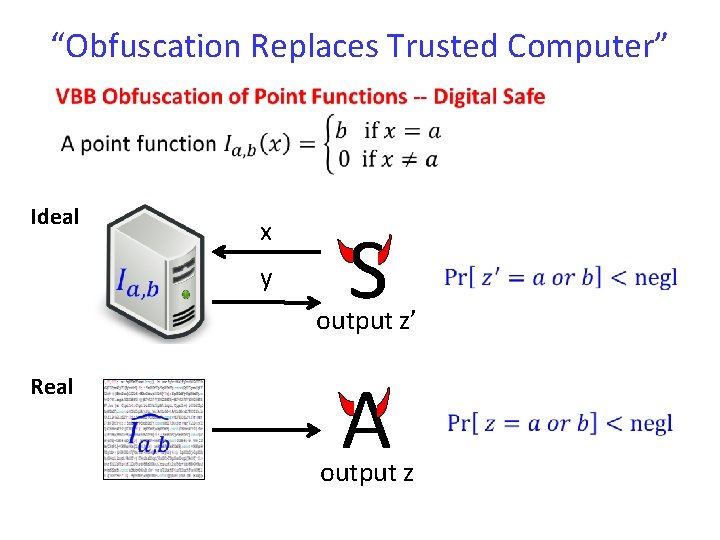
“Obfuscation Replaces Trusted Computer” Ideal x y S output z’ Real A output z

“Obfuscation Replaces Trusted Computer” Ideal Insecure: r can be maliciously chosen Real VBB has many applications! But, Infeasible [BGI+12]

Indistinguishability Obfuscator (i. O) [BGI+01] A output z 0 A output z 1 Obfuscation of equivalent programs are indistinguishable to efficient attackers

Indistinguishability Obfuscator (i. O) [BGI+01] A output z 0 A output z 1

i. O is still powerful Cryptomania PKE, Secure Multiparty Computation, Short signatures, Fully Homomorphic Encryption … Obfustopia Functional Encryption, Deniable Encryption, 2 -round adaptive secure MPC, Multiparty Key Exchange, Secret Sharing for NP, PPAD hardness, Succinct Garbling, . . . Powerful Abstraction for obtaining new results from classical assumptions

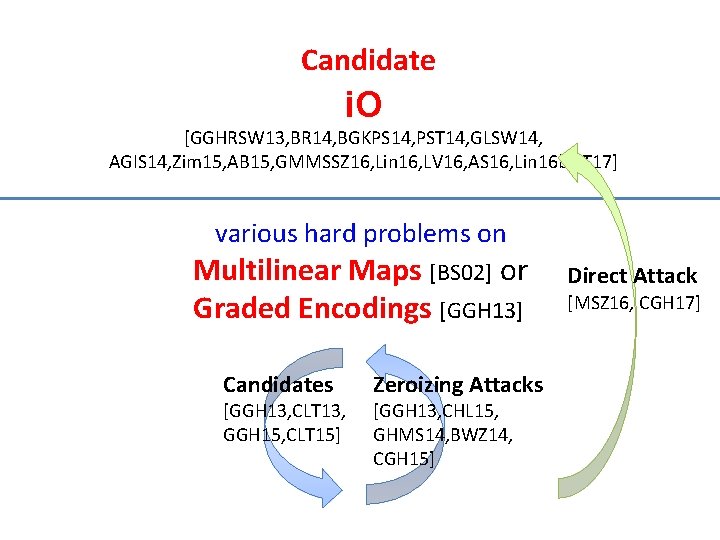
Candidate i. O [GGHRSW 13, BR 14, BGKPS 14, PST 14, GLSW 14, AGIS 14, Zim 15, AB 15, GMMSSZ 16, Lin 16, LV 16, AS 16, Lin 16 b, LT 17] various hard problems on Multilinear Maps [BS 02] or Graded Encodings [GGH 13] Candidates [GGH 13, CLT 13, GGH 15, CLT 15] Zeroizing Attacks [GGH 13, CHL 15, GHMS 14, BWZ 14, CGH 15] Direct Attack [MSZ 16, CGH 17]

(Asymmetric) Multilinear Maps [BS 02, Rot 13] [a] L = ga. L Encode in group GL: Multiply: [a 1]1 … [ai]i … [aj]j … � [a 1…a. D]D+1 Add/Sub: [ai] L [aj]L � [ai + aj] L [a. D]D Degree d (d = 2, Bilinear map ) Zero-Test (ZT): ZT( [a] D+1 ) = 1 iff a = 0

Graded Encoding Schemes (GES) [GGH 13] [a] L Encode with label L: Graded Multiply: [a 1]L 1 … [a[ai]i]L … [a[aj]j]L … L L ii jj � [a[a 1…a ] iaj] D D+1 Add/Sub: [ai] L [aj]L � [ai + aj] L [a. D]L D Label Structure: Labels “adds” up only if Pairable (Li, Lj) = 1 Zero-Test (ZT): ZT( [a] D+1 ) = 1 iff a = 0

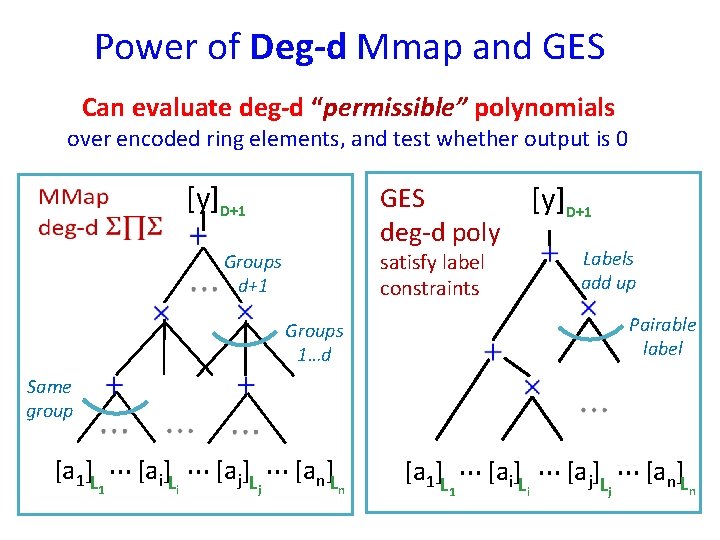
Power of Deg-d Mmap and GES Can evaluate deg-d “permissible” polynomials over encoded ring elements, and test whether output is 0 [y]D+1 GES deg-d poly Labels add up satisfy label constraints Groups d+1 Pairable label Groups 1…d Same group [a 1]L 1 … [ai]L … [aj]L … [an]L i j n

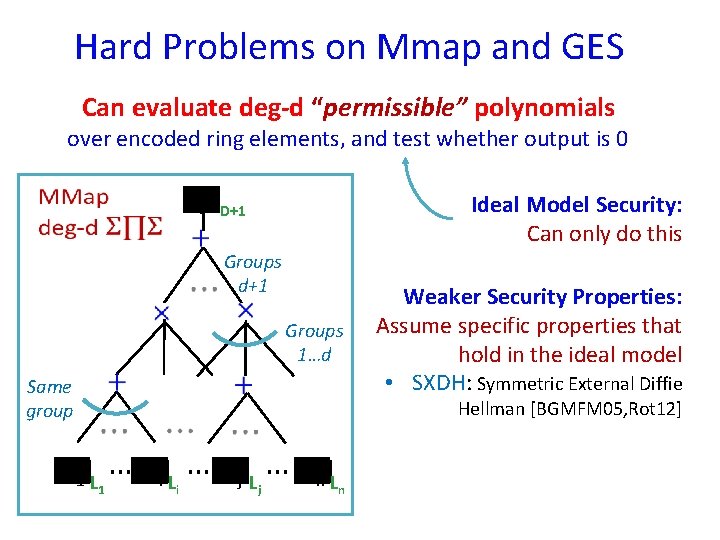
Hard Problems on Mmap and GES Can evaluate deg-d “permissible” polynomials over encoded ring elements, and test whether output is 0 [y]D+1 Ideal Model Security: Can only do this Groups d+1 Groups 1…d Same group [a 1]L Weaker Security Properties: Assume specific properties that hold in the ideal model • SXDH: Symmetric External Diffie Hellman [BGMFM 05, Rot 12] 1 … [ai]L … [aj]L … [an]L i j n

[a 1 a 2 a 3] 4 � [a 1]1 [a 2]2 [a 3]3 SXDH: Classical DDH on EACH source group { [a] L [b]L ≈ [b]L [ab] L [r]L } } a, b, r R given { [1] L’}

Deg-poly GES [GGHRSW 13…. ] • • Ideal model security MSEA [GLSW 14, GGHZ 16 + AJ 15/BV 15] Deg-O(1) GES [Lin 16] • DDH-like – joint-SXDH [LV 16] Locality O(1) PRG Tight: Deg = Locality Deg-5 GES [AS 16] • Close to ideal model security Deg-5 MMap [Lin 17] • SXDH Relax Deg-3 MMap [LT 17] • SXDH Bilinear Map Locality 5 PRG Locality 4 PRG Impossible [MST 03] Block Locality 3 PRG Block Locality 2 PRG Impossible [LV 17, BBKK 17] *

Theorem 1 [Lin 17] *: ∃a construction of IO from • SXDH on d-linear Mmaps • locality-d PRG • LWE Tight: Deg = Locality Relax Theorem 2 [LT 17]: Block-Locality-d PRG

Blockwise Local PRGs Locality L [CEMT 09, BQ 12, OW 14, AL 16] L = 5 [Gol 00, MST 03, OW 14] L < 5 impossible [MST 03] Blockwise Locality L Input Blocks

Preliminary Study on Blockwise Local PRG [LT 17] Natural Candidate: Goldreich’s local functions with input bits replaced by blocks 2, = L n Whe Thm [BBKK 17, LV 17]: Block-wise Locality 2 PRGs Do Not Exist * Except for a small window of expansion, not known to be sufficient for IO

Approaches for Constructing IO Direct Construction, Directly obfuscate a program Obfuscation of Branching Programs Obfuscation of Boolean Circuits

Obfuscation of Branching Program [GGHRSW 13, …] Obfuscation of Branching Program: … 1 … i … j l 1 i j l Require: high-degree, GES, with ideal security The label structure is used to prevent attacker from evaluating the program using inconsistent input bits

Approaches for Constructing IO Direct Construction, Directly obfuscate a program Obfuscation of Branching Programs Obfuscation of Boolean Circuits Bootstrapping Approach a simple primitive IO Functional Encryption for deg-3 polynomials deg-3 MMap with SXDH assumption

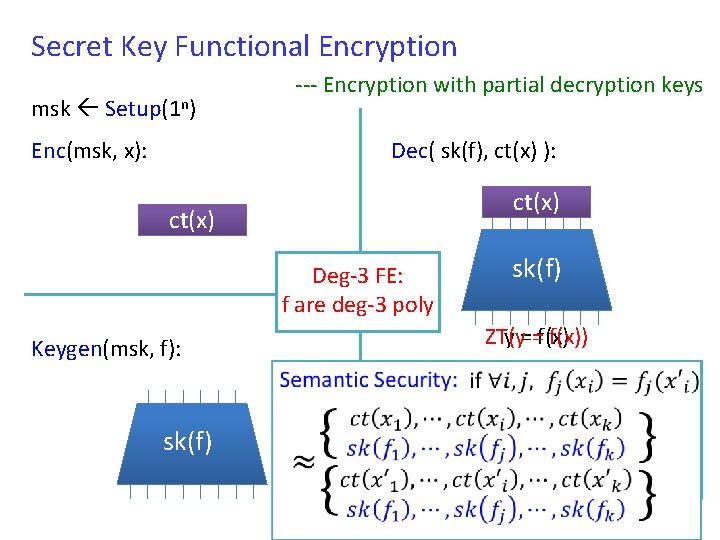
Secret Key Functional Encryption msk Setup(1 n) Enc(msk, x): --- Encryption with partial decryption keys Dec( sk(f), ct(x) ): ct(x) Deg-3 FE: f are deg-3 poly Keygen(msk, f): sk(f) ZT(y y ==f(x))

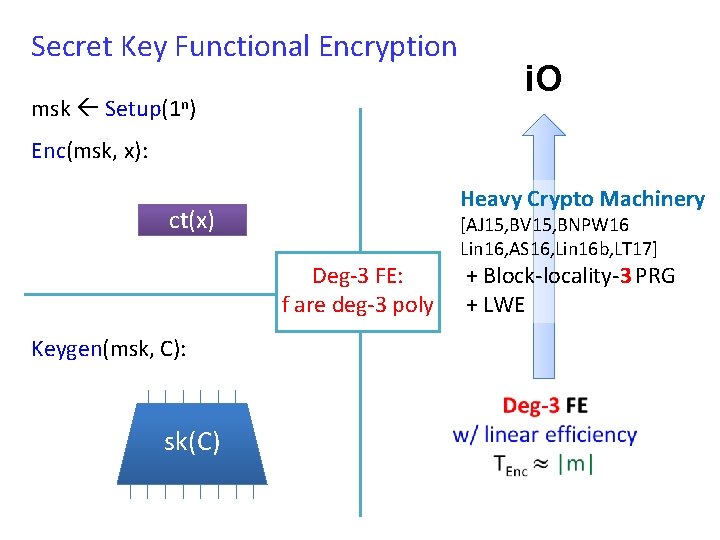
Secret Key Functional Encryption msk Setup(1 n) i. O Enc(msk, x): Heavy Crypto Machinery ct(x) [AJ 15, BV 15, BNPW 16 Lin 16, AS 16, Lin 16 b, LT 17] Deg-3 FE: f are deg-3 poly Keygen(msk, C): sk(C) + Block-locality-3 PRG + LWE

Deg-3 1 FE Deg-31 MMap [ABDP 15] a. k. a. Inner Product Encryption (IPE) 1 SK(y) 1 CT(x) 1 Dec ZT(<x, y>) One ciphertext only [s + x] 1 and [s + x’] 1 gives [x-x’] 1 1 MSK = 1 SK(y) = <s, y> y 1 CT(x) = [-1]1 [ s + x] 1 “< 1 CT(x), 1 SK(y) >” = [-<s, y>] 1 + [<s, y> + <x, y>] 1 = [<x, y>] 1 Dec

Deg-1 FE Deg-1 MMap [ABDP 15] a. k. a. Inner Product Encryption (IPE) 1 SK(y) 1 CT(x) 1 Dec ZT(<x, y>) 1 MSK = 1 SK(y) = <s, y> y 1 CT(x) = [-r] 1 [ rs+ x] “< 1 CT(x), 1 SK(y) >” = [-<rs, y>] 1+ [<rs, y> + <x, y>] 1 = [<x, y>] 1 Dec

Strengthen Security of IPE a. k. a. Inner Product Encryption (IPE) 1 SK(y) 1 CT(x) 1 MSK 1 Dec ZT(<x, y>) = 1 SK(y) = <s, y> y 1 CT(x) = [-r] 1 [ rs+ x] 1 “< 1 CT(x), 1 SK(y) >” = [<x, y>] 1 So far, hide only x Func Hiding: Also hide y Idea: View 1 SK(y) as a vector Encrypt it using IPE

Func Hiding IPE Bilinear Maps [Lin 16 b] a. k. a. Inner Product Encryption (IPE) 1 SK(y) 1 CT(x) 1 Dec So far, hide only ZT(<x, y>) x Func Hiding: Also hide y 1 MSK ) h. MSK = h. SK(y) = 1 CT( 1 SK(y) ) h. CT(x) = 1 SK( 1 CT(x) ) “< h. CT(x), h. SK(y) >”= “< 1 CT(x), 1 SK(y) >” = [<x, y>] Bilinear pairing

Deg-2 FE Deg-2 MMap [Lin 16 b] Starting Point: 2 MSK = 2 SK(f) = 1 SK(C) = <S, C> = C [-r] S is random, cannot be compressed

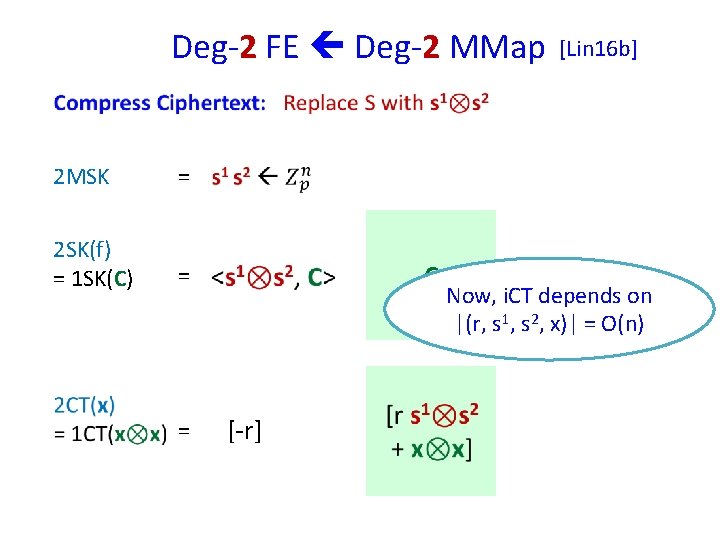
Deg-2 FE Deg-2 MMap 2 MSK = 2 SK(f) = 1 SK(C) = = C [-r] [Lin 16 b] Now, i. CT depends on |(r, s 1, s 2, x)| = O(n)

Deg-2 FE Deg-2 MMap 2 MSK = 2 SK(f) = 1 SK(C) = C h. Dec = [-r]

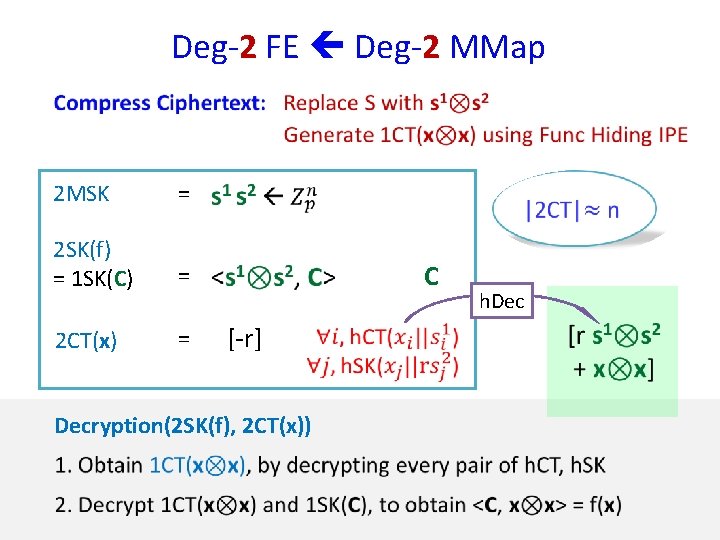
Deg-2 FE Deg-2 MMap 2 MSK = 2 SK(f) = 1 SK(C) = 2 CT(x) = C [-r] Decryption(2 SK(f), 2 CT(x)) h. Dec

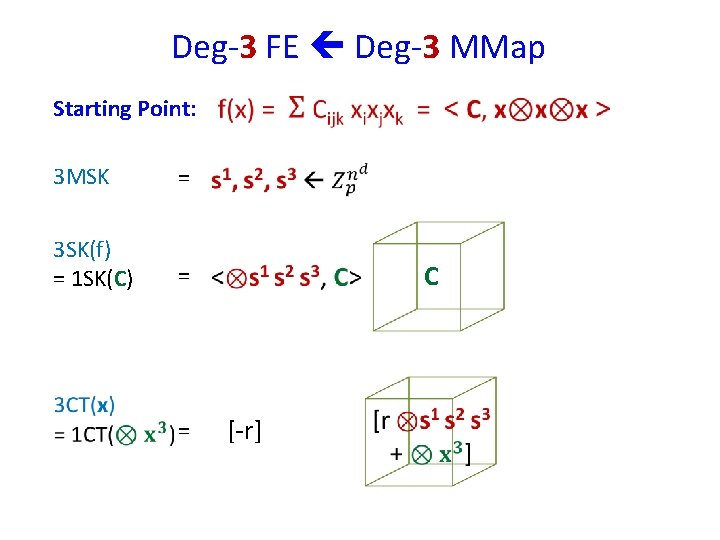
Deg-3 FE Deg-3 MMap Starting Point: 3 MSK = 3 SK(f) = 1 SK(C) = = C [-r]

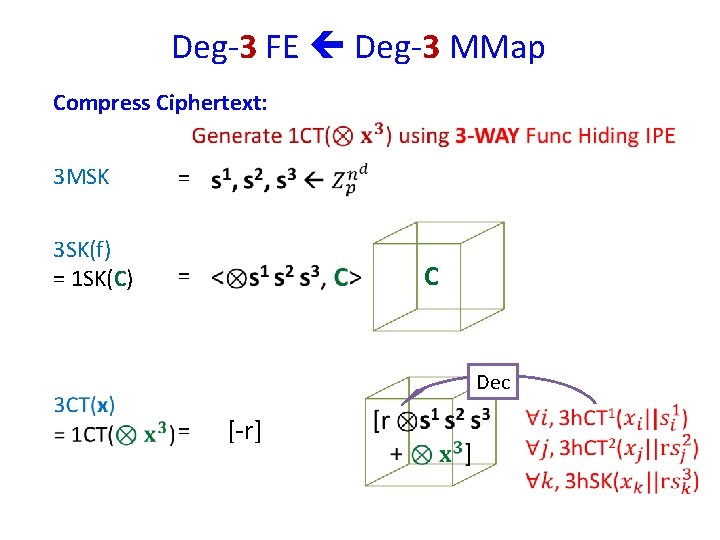
Deg-3 FE Deg-3 MMap Compress Ciphertext: 3 MSK = 3 SK(f) = 1 SK(C) = C Dec = [-r]

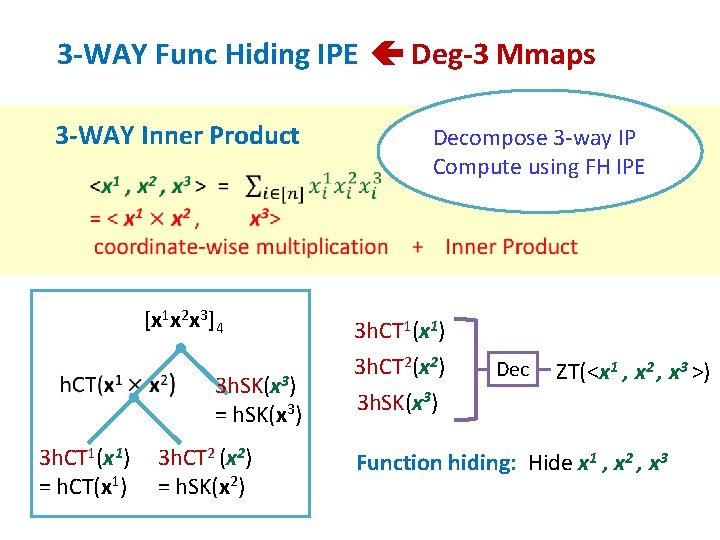
3 -WAY Func Hiding IPE Deg-3 Mmaps 3 -WAY Inner Product [x 1 x 2 x 3]4 3 h. SK(x 3) = h. SK(x 3) 3 h. CT 1(x 1) = h. CT(x 1) 3 h. CT 2 (x 2) = h. SK(x 2) Decompose 3 -way IP Compute using FH IPE 3 h. CT 1(x 1) 3 h. CT 2(x 2) 3 h. SK(x 3) Dec ZT(<x 1 , x 2 , x 3 >) Function hiding: Hide x 1 , x 2 , x 3

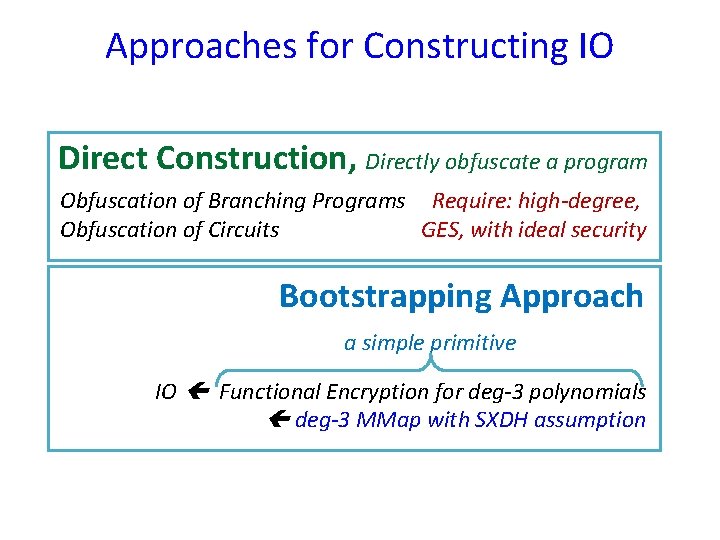
Approaches for Constructing IO Direct Construction, Directly obfuscate a program Obfuscation of Branching Programs Require: high-degree, Obfuscation of Circuits GES, with ideal security Bootstrapping Approach a simple primitive IO Functional Encryption for deg-3 polynomials deg-3 MMap with SXDH assumption

Thank you!