Indipendenza tra due caratteri Definizioni 1 due caratteri

























![Per il data set (a) sono prevalenti i prodotti degli scarti [(xi - M(X)] Per il data set (a) sono prevalenti i prodotti degli scarti [(xi - M(X)]](https://slidetodoc.com/presentation_image_h2/5e7344ba54d9d30394a2822c45bfcb38/image-43.jpg)



![Nel data set (c) sono prevalenti i prodotti di scarti negativi, cioè [(xi-M(X)] × Nel data set (c) sono prevalenti i prodotti di scarti negativi, cioè [(xi-M(X)] ×](https://slidetodoc.com/presentation_image_h2/5e7344ba54d9d30394a2822c45bfcb38/image-50.jpg)


















- Slides: 78

Indipendenza tra due caratteri Definizioni: 1) due caratteri sono indipendenti se tra essi non esiste una relazione di causa ed effetto; 2) due caratteri sono indipendenti se la conoscenza di una modalità di uno dei due caratteri non migliora la previsione sulla modalità dell’altro; 1

Esempio di Distribuzione Bivariata: X/Y y 1 y 2 y 3 y 4 Tot. x 1 x 2 x 3 Tot. X x 1 x 2 x 3 Tot. f(X|y 1) 12/36=0. 33 15/36=0. 42 9/36=0. 25 1. 00 12 15 9 36 4 5 3 12 f(X|y 2) 4/12=0. 33 5/12=0. 42 3/12=0. 25 1. 00 16 20 12 48 f(X|y 3) 16/48=0. 33 20/48=0. 42 12/48=0. 25 1. 00 8 10 6 24 40 50 30 120 f(X|y 4) 8/24=0. 33 10/24=0. 42 6/24=0. 25 1. 00 f(X) 40/120=0. 33 50/120=0. 42 30/120=0. 25 1. 00 Domanda: se sulla 121^ unità si rileva Y=y 3 questa informazione migliora la nostra previsione su quale potrebbe essere il valore di X? La risposta è NO! Perché il sapere che Y=y 3 non aggiunge nulla rispetto all’informazione che ci viene 2 data dalla semplice distribuzione marginale di X.

Pertanto possiamo concludere che: X è indipendente da Y Y y 1 f(Y|x 1) 12/40=0. 30 f(Y|x 2) 15/50=0. 30 f(Y|x 3) 9/30=0. 30 f(Y) 36/120=0. 30 y 2 4/40=0. 10 5/50=0. 10 3/30=0. 10 12/120=0. 10 y 3 16/40=0. 40 20/50=0. 40 12/30=0. 40 48/120=0. 40 y 4 8/40=0. 20 10/50=0. 20 6/30=0. 20 24/120=0. 20 Tot. 1. 00 Nota: se tutte le distribuzioni di X condizionate ad Y sono uguali tra loro ed uguali alla marginale di X anche tutte le distribuzioni di Y condizionate ad X sono uguali tra loro ed uguali alla marginale di Y. Pertanto, anche in questo caso, se sulla 121^ unità dovessere rilevato, ad esempio, X=x 1 la nostra previsione circa la modalità di Y non migliorerebbe rispetto all’informazione che ci viene data dalla distribuzione marginale della stessa Y. Quindi Y è indipendente da X. Domanda: come sono le medie condizionate di X e di Y? 3

Tornando, invece, alle 100 barrette d’acciaio ed esaminando la tabelle distribuzioni di Y condizionate ad X, sapendo, ad esempio che: 0<X<0, 75 quale previsione potremmo fare su Y? Y f( Y| x 1 ) f( Y| x 2 ) f( Y| x 3 ) f( Y| x 4 ) 2 -4 0, 7143 0, 1667 0, 0571 0, 0000 4 -5 0, 2857 0, 5417 0, 1714 0, 0000 5 -6 0, 0000 0, 2500 0, 1429 0, 2000 6 -7 0, 0000 0, 0417 0, 4286 0, 3500 7 -9 0, 0000 0, 2000 0, 4500 Totali 1, 0000 4

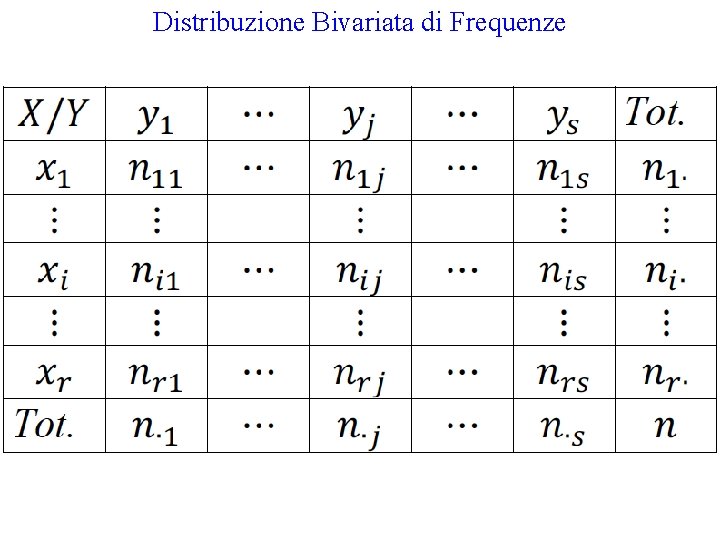
Distribuzione Bivariata di Frequenze

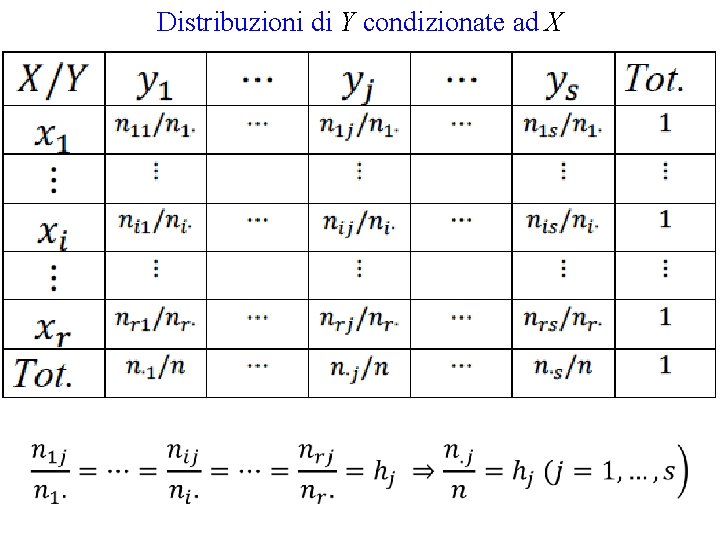
Distribuzioni di X condizionate ad Y




DIMOSTRAZIONE da cui: cioè se le distribuzioni di X condizionate ad Y sono uguali tra di loro allora esse saranno uguali alla distribuzione marginale di X, ovvero:

Distribuzioni di Y condizionate ad X

DIMOSTRAZIONE Dalla dimostrazione precedente abbiamo ottenuto che se le distribuzioni di X condizionate ad Y sono uguali tra loro allora: ma da questa otteniamo anche che: cioè che (a) le distribuzioni di Y condizionate ad X sono uguali tra di loro ed anche (b) esse saranno uguali alla distribuzione marginale di Y.

Infine, poiché le distribuzioni di X condizionate ad Y sono uguali tra loro e conseguentemente anche le distribuzioni di Y condizionate ad X sono uguali tra loro, potremo concludere dicendo che X ed Y sono indipendenti e la condizione d’indipendenza è:

Teorema: Se (1) f(xi|y 1)=. . . =f(xi|yj)=… =f(xi|ys)=ki per (i=1, . . , r) cioè se: ni 1 / n. 1=…= nij / n. j =…= nis / n. s= ki per (i=1, . . , r) allora: (2) f(xi)=ki per (i=1, . . , r), cioè: ni. / n = ki per (i=1, . . , r); (3) f(yj|x 1)=. . . =f(yj|xi)=. . . =f(yj|xr)=hj per (j=1, . . , s) cioè: n 1 j / n 1. =…= nij / ni. =…= nrj / nr. = hj per (j=1, . . , s); (4) f(yj)=hj per (j=1, . . , s), cioè: n. j / n = hj per (j=1, . . , s) ed infine: (5) X è indipendente da Y e Y è indipendente da X. 14

Dimostrazione: dalla (1) avremo che: ni 1 / n. 1 =. . . = nij / n. j =. . . = nis / n. s = ki cioè: ni 1 = n. 1 ki; …. ; nij = n. j ki; …. ; nis = n. s ki sommando membro avremo che: cioè per (i=1, . . , r) ovvero: ki = ni. / n per (i=1, . . , r), che dimostra la (2). 15

Da (1) e (2) deduciamo che: f(xi|yj) = f(xi) = ki per (i=1, . . , r) e (j=1, . . , s) che equivale a: per (i=1, . . , r) e (j=1, . . , s) da cui: per (i=1, . . , r) e (j=1, . . , s) che dimostrano la (3) e la (4). Se sono tutte vere: (1), (2), (3) e (4) esse implicano anche la (5), che è dalle stesse definita. Infine la condizione di Indipendenza Statistica tra X e Y è data da: per (i=1, . . , r) e (j=1, . . , s) c. d. d. . 16

In sintesi, abbiamo dimostrato che: {indipendenza} { f(xi|yj)=f(xi)} { f(yj|xi)=f(yj)}; i, j ovvero: {indipendenza} {nij/n. j = ni. /n} {nij/ni. = n. j/n}; i, j Condizione d’Indipendenza: Verificare la condizione d’indipendenza sulle ultime due distribuzioni bivariate (pagine 138 e 144). 17

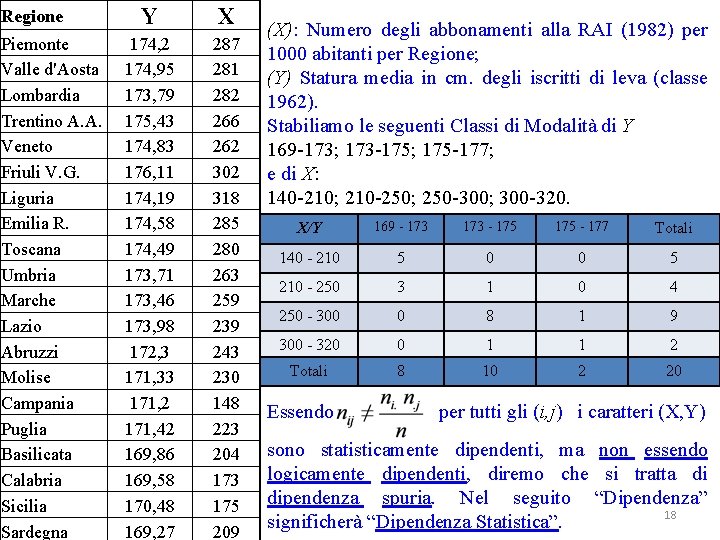
Regione Piemonte Valle d'Aosta Lombardia Trentino A. A. Veneto Friuli V. G. Liguria Emilia R. Toscana Umbria Marche Lazio Abruzzi Molise Campania Puglia Basilicata Calabria Sicilia Sardegna Y X 174, 2 174, 95 173, 79 175, 43 174, 83 176, 11 174, 19 174, 58 174, 49 173, 71 173, 46 173, 98 172, 3 171, 33 171, 2 171, 42 169, 86 169, 58 170, 48 169, 27 281 282 266 262 302 318 285 280 263 259 239 243 230 148 223 204 173 175 209 (X): Numero degli abbonamenti alla RAI (1982) per 1000 abitanti per Regione; (Y) Statura media in cm. degli iscritti di leva (classe 1962). Stabiliamo le seguenti Classi di Modalità di Y 169 -173; 173 -175; 175 -177; e di X: 140 -210; 210 -250; 250 -300; 300 -320. X/Y 169 - 173 - 175 - 177 Totali 140 - 210 5 0 0 5 210 - 250 3 1 0 4 250 - 300 0 8 1 9 300 - 320 0 1 1 2 Totali 8 10 2 20 Essendo per tutti gli (i, j) i caratteri (X, Y) sono statisticamente dipendenti, ma non essendo logicamente dipendenti, diremo che si tratta di dipendenza spuria. Nel seguito “Dipendenza” 18 significherà “Dipendenza Statistica”.

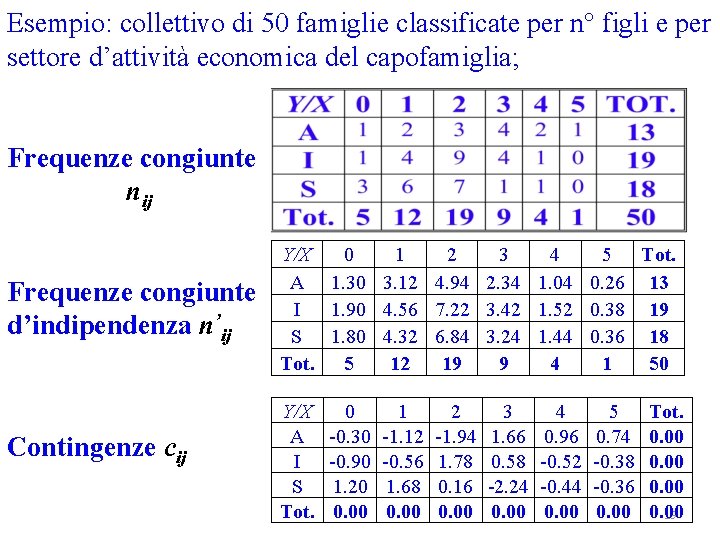
Esempio: collettivo di 50 famiglie classificate per n° figli e per settore d’attività economica del capofamiglia; Frequenze congiunte nij Frequenze congiunte d’indipendenza n’ij Contingenze cij Y/X 0 1 2 3 4 5 Tot. A 1. 30 3. 12 4. 94 2. 34 1. 04 0. 26 13 I 1. 90 4. 56 7. 22 3. 42 1. 52 0. 38 19 S 1. 80 4. 32 6. 84 3. 24 1. 44 0. 36 18 Tot. 5 12 19 9 4 1 50 Y/X A I S Tot. 0 -0. 30 -0. 90 1. 20 0. 00 1 -1. 12 -0. 56 1. 68 0. 00 2 -1. 94 1. 78 0. 16 0. 00 3 1. 66 0. 58 -2. 24 0. 00 4 0. 96 -0. 52 -0. 44 0. 00 5 0. 74 -0. 38 -0. 36 0. 00 Tot. 0. 00 19

Misure sintetiche di Dipendenza Statistica Indice Chi-Quadro di Pearson: dove le cij = (nij – n’ij ) e le n’ij = (ni. n. j / n ). Proprietà di χ2: a) se X ed Y sono indipendenti allora χ2 = 0; b) se X ed Y non sono indipendenti χ2 > 0, ed è tanto più grande quanto più le nij si differenziano dalle n’ij ; c) χ2 è una misura di dipendenza per X ed Y caratteri quantitativi e/o qualitativi ed il suo calcolo non si basa né sulle modalità di X né su quelle di Y; d) χ2 è una misura assoluta di dipendenza statistica. 20

χ 2: Calcolo di 1)Tabella dati originari: nij; 2)Tabella di Indipendenza: n’ij; 3)Tabella delle contingenze: cij; 4)Tabella dei rapporti: c 2 ij / n’ij; 5) χ2=10, 49. Y/X A I S Tot. 0 1 1 3 5 1 2 4 6 12 2 3 9 7 19 3 4 4 1 9 4 2 1 1 4 5 1 0 0 1 Tot. 13 19 18 50 Y/X A I S Tot. 0 1, 3 1, 9 1, 8 5 1 3, 12 4, 56 4, 32 12 2 4, 94 7, 22 6, 84 19 3 2, 34 3, 42 3, 24 9 4 1, 04 1, 52 1, 44 4 5 0, 26 0, 38 0, 36 1 Tot. 13 19 18 50 Y/X A I S Tot. 0 -0, 3 -0, 9 1, 2 0 1 -1, 12 -0, 56 1, 68 0 2 -1, 94 1, 78 0, 16 0 3 1, 66 0, 58 -2, 24 0 4 0, 96 -0, 52 -0, 44 0 5 0, 74 -0, 38 -0, 36 0 Tot. 0 0 Y/X A I S Tot. 0 0, 07 0, 43 0, 80 1, 30 1 0, 40 0, 07 0, 65 1, 12 2 0, 76 0, 44 0, 00 1, 20 3 1, 18 0, 10 1, 55 2, 82 4 0, 89 0, 18 0, 13 1, 20 5 2, 11 0, 38 0, 36 2, 85 Tot. 5, 40 1, 59 3, 50 10, 49 Nota: il valore di χ2 ottenuto ci assicura che tra X ed Y c’è dipendenza statistica ma non dice quanto essa è forte, perché 21 χ2 è una misura assoluta di dipendenza.

Calcolo alternativo di χ2: poiché :

Pertanto avremo anche: infine, se non si vuole passare per il calcolo delle n’ij=ni. n. j / n, avremo: 23

Definizione di Massima Dipendenza La dipendenza è massima se per ogni riga o per ogni colonna non più di una frequenza congiunta è diversa da zero. Esempio: X/Y x 1 x 2 x 3 Tot. y 1 n 11 0 0 n 11 y 2 0 0 n 32 y 3 0 n 23 y 4 0 0 Tot. n 11 n 23 n 32 n Per le caselle con nij ≠ 0 avremo: n 2 ij = ni. n. j e di conseguenza , dove t = minore ( r , s ) e max χ2 =( t – 1) n Definiamo, quindi, l’indice relativo di dipendenza di Cràmer: C 2 = χ2/ max χ2 = χ2/ [ ( t – 1 ) n ] con [0 ≤ C 2 ≤ 1]. 24

Esempio collettivo di 50 famiglie classificate per n° figli e per settore d’attività economica del capofamiglia: Il max χ2 per la tabella precedente è quello che si otterrebbe da una tabella con le stesse dimensioni (3 x 6) e con lo stesso totale (n=50). In tal caso: max χ2 = ( t – 1 ) n = [ min (3, 6) – 1 ] 50 = 100, quindi: C 2 = χ2/max χ2 = 10, 49/100 = 0, 1049

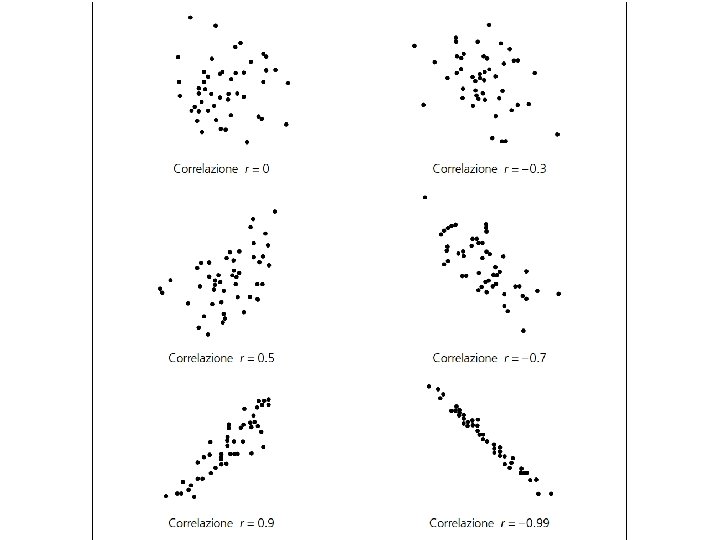
Misure di dipendenza lineare o correlazione Se due caratteri quantitativi risultano “statisticamente dipendenti” possiamo ipotizzare che essi siano legati da una relazione lineare, cioè del tipo Y= a + b X. Per verificare questa ipotesi misureremo la: “strettezza della relazione lineare, ovvero, misurando il grado di correlazione tra X e Y”. Si considerino le coppie di modalità (xi , yj), riportati nelle tabelle che seguono, ed i relativi di diagrammi scatter che mettono in luce una possibile relazione lineare tra X e Y: 26

Data Set (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y X 1, 00 1, 30 1, 00 1, 60 1, 70 1, 50 2, 00 2, 40 3, 00 3, 60 4, 00 4, 10 5, 00 5, 40 5, 00 5, 20 5, 00 Y -3, 70 14, 53 -3, 62 -4, 46 -1, 54 -7, 99 10, 86 11, 97 9, 11 -11, 32 -6, 60 2, 83 5, 71 9, 73 -7, 08 7, 64 13, 74 -1, 76 3, 66 -6, 50 5, 54 19, 50 -6, 96 3, 47 14, 39 X 6, 00 6, 60 7, 00 7, 10 7, 00 7, 80 8, 00 8, 70 8, 00 8, 20 8, 00 9, 10 9, 00 9, 60 10, 00 10, 30 10, 00 Y -1, 98 2, 42 6, 03 -7, 16 -1, 70 19, 24 -7, 68 9, 32 9, 02 15, 06 19, 28 19, 33 17, 56 7, 99 19, 50 13, 02 2, 40 11, 69 17, 11 -1, 30 17, 32 16, 51 4, 00 -5, 79 20, 30 X 11, 00 10, 30 11, 00 11, 40 12, 00 12, 10 13, 00 13, 40 13, 00 14, 50 14, 00 14, 20 15, 00 16, 00 Y 24, 07 -4, 60 12, 81 -1, 16 10, 76 5, 14 21, 17 7, 38 25, 59 14, 81 9, 64 24, 97 0, 54 24, 08 0, 26 0, 33 23, 64 2, 79 14, 89 -2, 37 14, 56 1, 66 17, 61 3, 23 5, 68 X 17, 00 17, 40 18, 00 18, 10 19, 00 20, 30 21, 00 22, 90 23, 10 24, 00 25, 10 25, 00 26, 70 26, 00 26, 20 27, 00 28, 20 29, 00 Y 13, 06 6, 18 12, 10 15, 31 7, 33 12, 97 13, 56 9, 45 26, 55 14, 07 22, 42 26, 72 29, 89 33, 89 14, 39 15, 87 9, 13 15, 41 29, 08 17, 58 22, 06 10, 48 25, 73 27 15, 30 18, 37

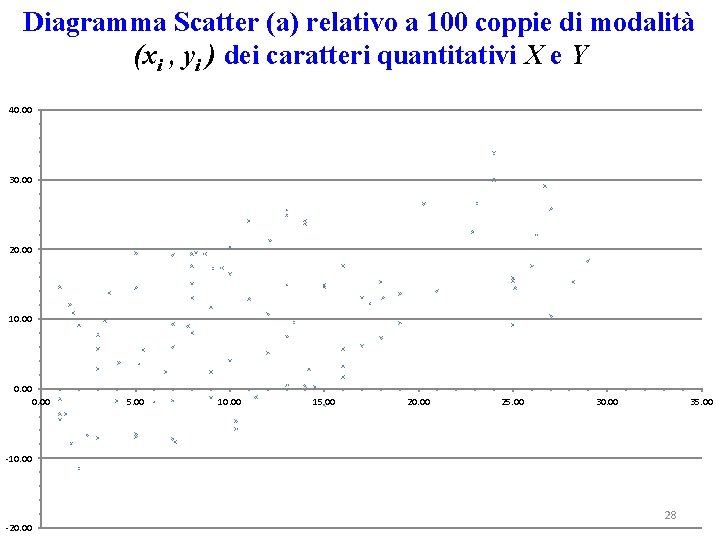
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 30. 00 20. 00 10. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 -10. 00 -20. 00 28

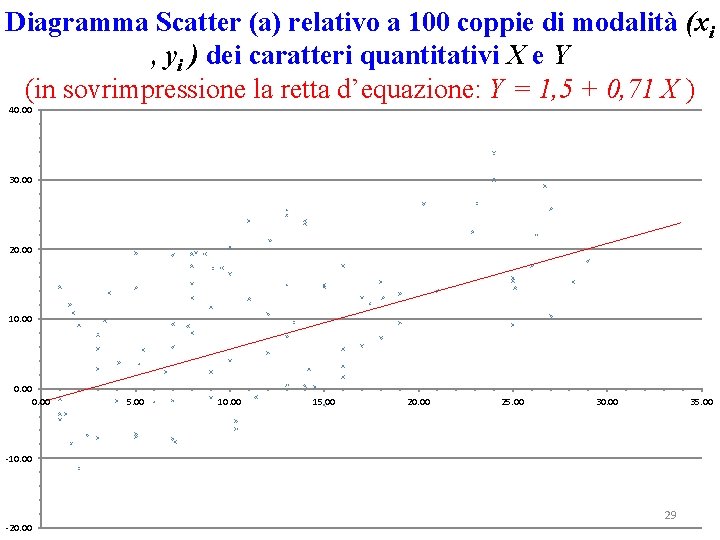
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y (in sovrimpressione la retta d’equazione: Y = 1, 5 + 0, 71 X ) 40. 00 30. 00 20. 00 10. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 -10. 00 -20. 00 29

Data Set (b) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 30

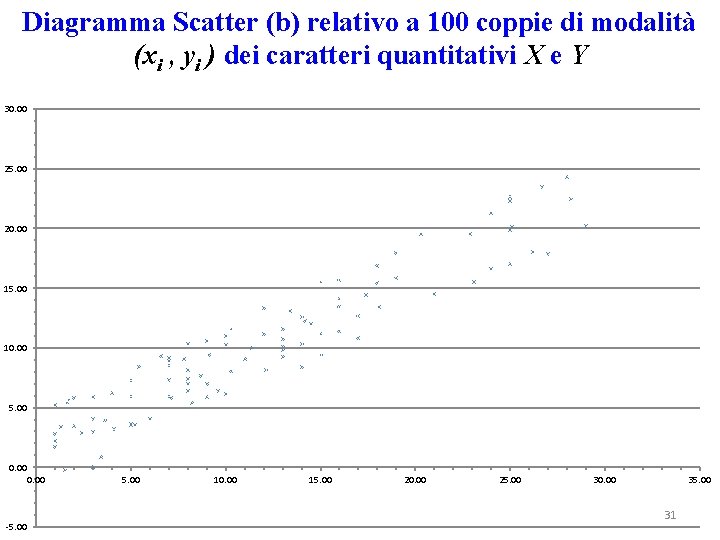
Diagramma Scatter (b) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 30. 00 25. 00 20. 00 15. 00 10. 00 5. 00 0. 00 -5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 31

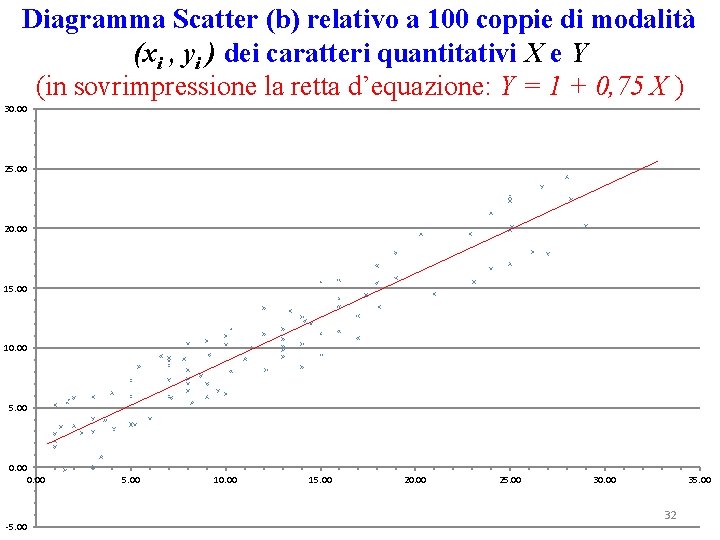
Diagramma Scatter (b) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y (in sovrimpressione la retta d’equazione: Y = 1 + 0, 75 X ) 30. 00 25. 00 20. 00 15. 00 10. 00 5. 00 0. 00 -5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 32

La differenza tra i due diagrammi scatter (a) e (b) consiste nel fatto che il primo diagramma mostra una nuvola di punti più dispersa che non nel secondo caso, pur mostrando entrambe una sottostante relazione lineare tra X e Y. Più precisamente diremo che nel caso (b) la relazione lineare tra X e Y è più stretta che non nel caso (a). Misure di strettezza della relazione lineare o di Correlazione tra X e Y La Covarianza Date le n coppie di modalità (x 1, y 1)……(xn, yn) chiameremo Covarianza la media dei prodotti degli scarti dalle rispettive medie di X e di Y: 33

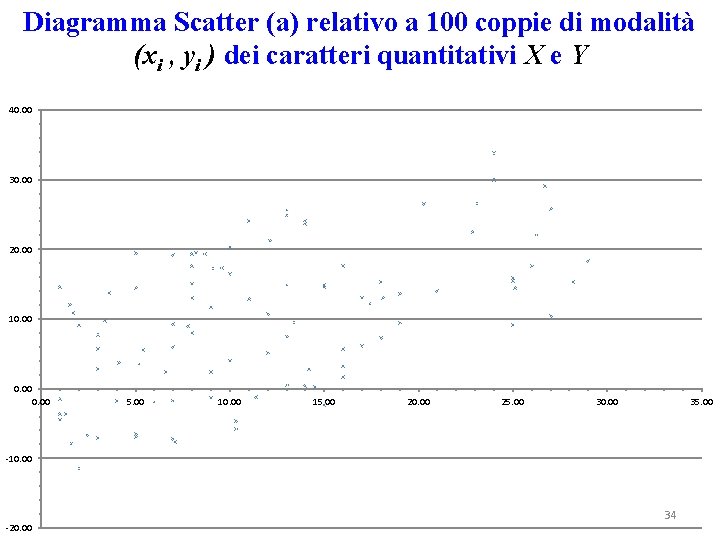
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 30. 00 20. 00 10. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 -10. 00 -20. 00 34

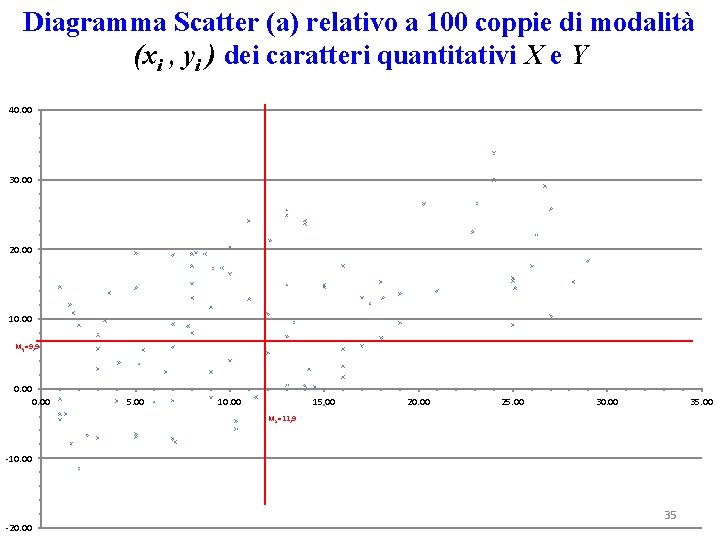
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 30. 00 20. 00 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 -10. 00 -20. 00 35

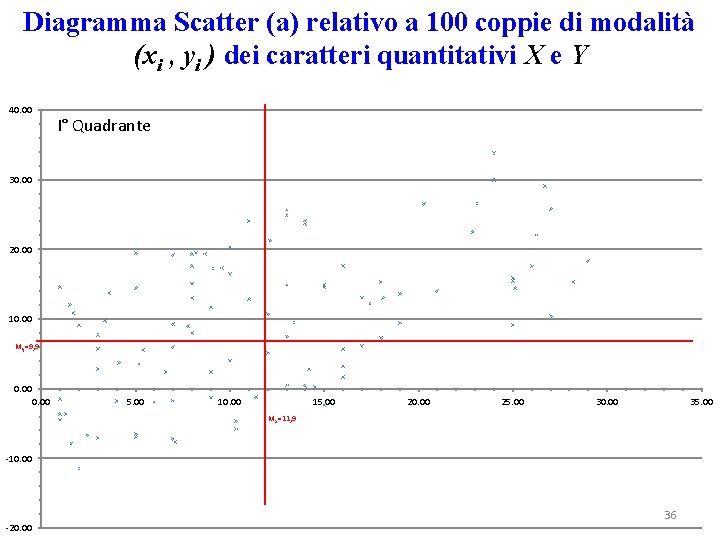
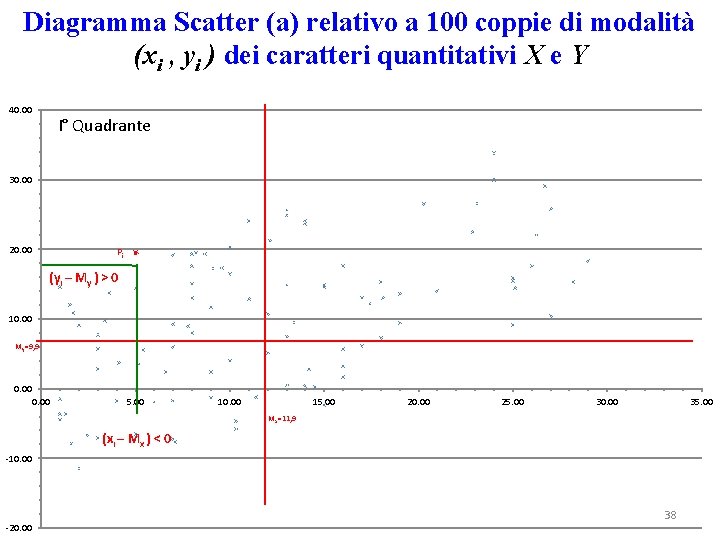
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 I° Quadrante 30. 00 20. 00 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 -10. 00 -20. 00 36

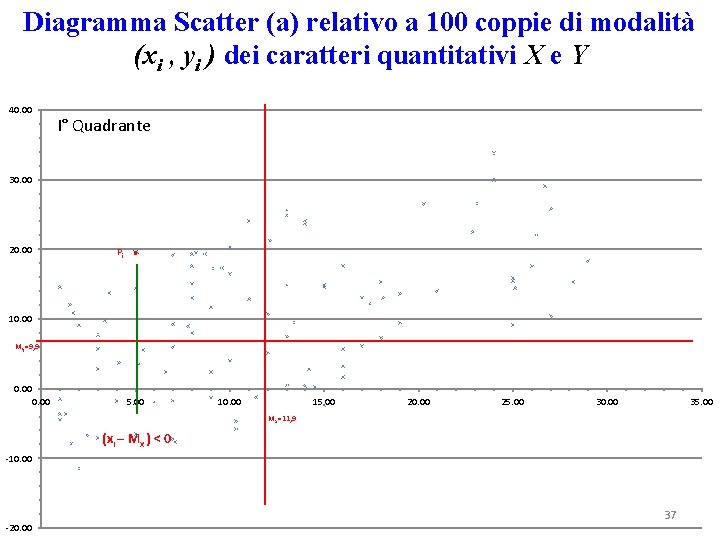
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 I° Quadrante 30. 00 20. 00 Pi 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 (xi – Mx ) < 0 -10. 00 -20. 00 37

Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 I° Quadrante 30. 00 20. 00 Pi (yi – My ) > 0 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 (xi – Mx ) < 0 -10. 00 -20. 00 38

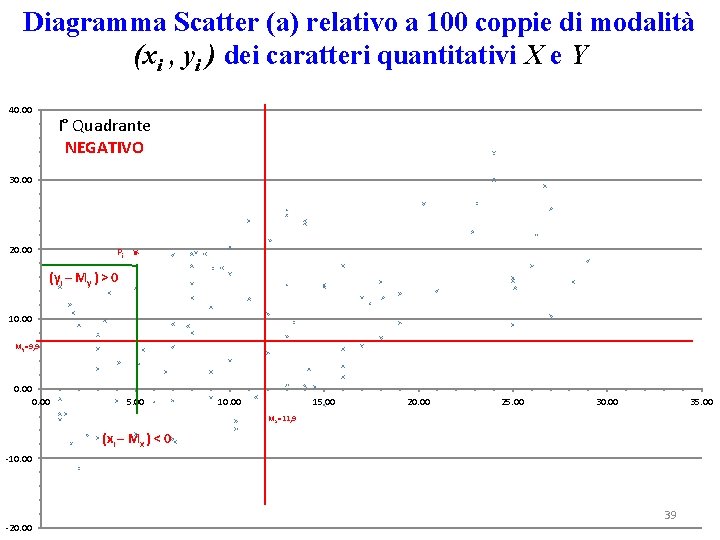
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 I° Quadrante NEGATIVO 30. 00 20. 00 Pi (yi – My ) > 0 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 (xi – Mx ) < 0 -10. 00 -20. 00 39

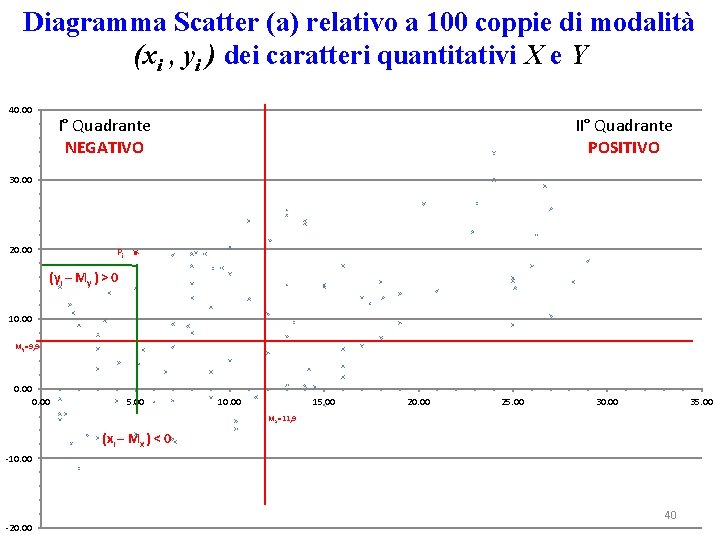
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 I° Quadrante NEGATIVO II° Quadrante POSITIVO 30. 00 20. 00 Pi (yi – My ) > 0 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 (xi – Mx ) < 0 -10. 00 -20. 00 40

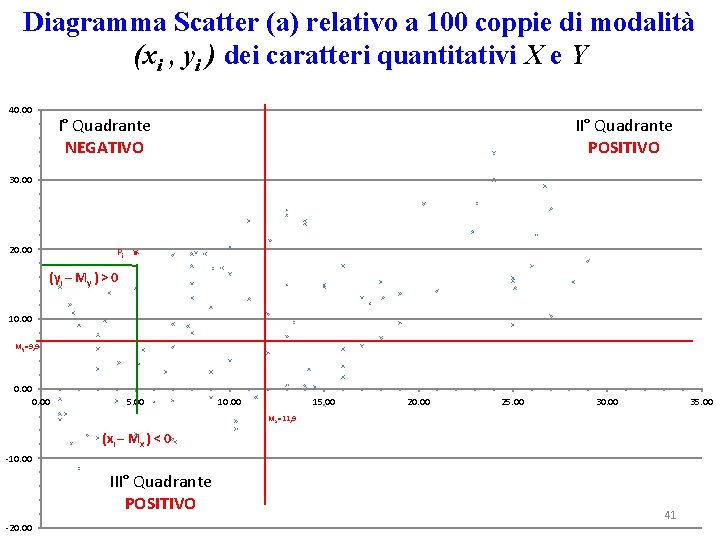
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 I° Quadrante NEGATIVO II° Quadrante POSITIVO 30. 00 20. 00 Pi (yi – My ) > 0 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 (xi – Mx ) < 0 -10. 00 III° Quadrante POSITIVO -20. 00 41

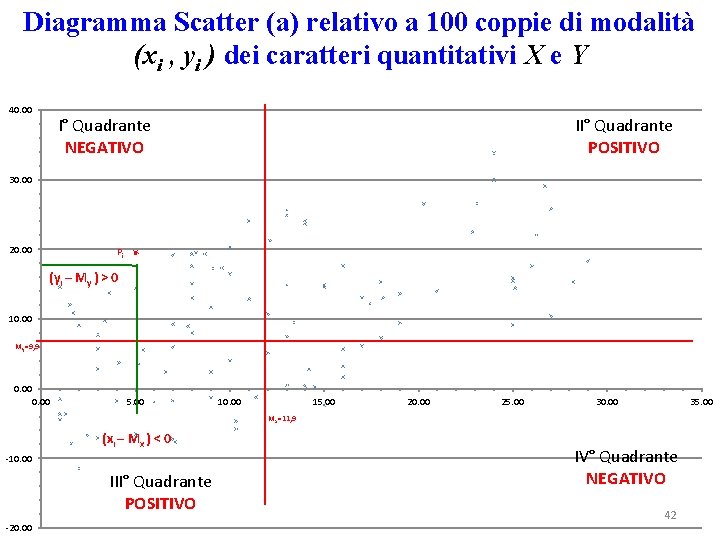
Diagramma Scatter (a) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 40. 00 I° Quadrante NEGATIVO II° Quadrante POSITIVO 30. 00 20. 00 Pi (yi – My ) > 0 10. 00 My=9, 9 0. 00 5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00 Mx=11, 9 (xi – Mx ) < 0 -10. 00 III° Quadrante POSITIVO -20. 00 IV° Quadrante NEGATIVO 42
![Per il data set a sono prevalenti i prodotti degli scarti xi MX Per il data set (a) sono prevalenti i prodotti degli scarti [(xi - M(X)]](https://slidetodoc.com/presentation_image_h2/5e7344ba54d9d30394a2822c45bfcb38/image-43.jpg)
Per il data set (a) sono prevalenti i prodotti degli scarti [(xi - M(X)] × [yi – M(Y)] > 0 , essendo X ed Y concordi, quindi in particolare: Cov(X, Y)>0 , Cov(X, Y) = 41, 42.

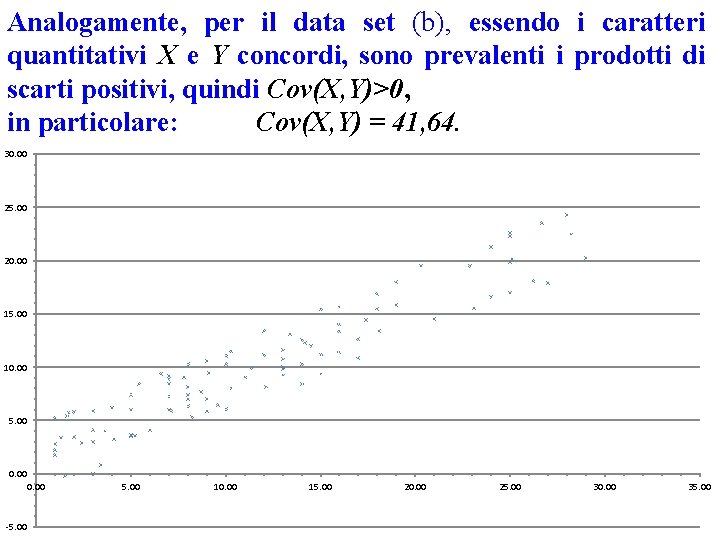
Analogamente, per il data set (b), essendo i caratteri quantitativi X e Y concordi, sono prevalenti i prodotti di scarti positivi, quindi Cov(X, Y)>0, in particolare: Cov(X, Y) = 41, 64. 30. 00 25. 00 20. 00 15. 00 10. 00 5. 00 0. 00 -5. 00 10. 00 15. 00 20. 00 25. 00 30. 00 35. 00

Analogamente, per il data set (b), essendo i caratteri quantitativi X e Y concordi, sono prevalenti i prodotti di scarti positivi, quindi Cov(X, Y)>0, in particolare: Cov(X, Y) = 41, 64. 30. 00 II° Quadrante POSITIVO I° Quadrante NEGATIVO 25. 00 20. 00 15. 00 10. 00 My=10, 3 IV° Quadrante NEGATIVO 5. 00 0. 00 -5. 00 III° Quadrante POSITIVO 10. 00 Mx=11, 9 15. 00 20. 00 25. 00 30. 00 35. 00

Se X ed Y sono concordi sono prevalenti i punti che cadono nel II° e nel III° quadrante. A tali punti corrispondono scarti di X e di Y che hanno, rispettivamente, lo stesso segno e che producono, pertanto, prodotti di scarti positivi. La Covarianza, essendo pari alla media dei prodotti degli scarti, sarà positiva. Nel caso in cui X ed Y siano discordi i punti del diagramma scatter saranno prevalenti nel I° e nel IV° quadrante. A tali punti corrisponderanno scarti di X e di Y che avranno segno opposto e daranno luogo, pertanto, a prodotti di scarti negativi. La Covarianza, in questo secondo caso, essendo pari alla media dei prodotti degli scarti, sarà negativa. 46

Data Set (c) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y X Y X Y 1, 00 23, 94 6, 00 18, 37 11, 00 19, 17 17, 00 7, 80 1, 00 21, 20 6, 60 22, 22 10, 30 13, 95 17, 00 13, 15 1, 30 24, 83 7, 00 21, 30 11, 00 16, 49 17, 40 11, 26 1, 00 21, 85 7, 00 17, 87 11, 40 13, 47 18, 00 13, 36 1, 00 25, 48 7, 00 15, 97 12, 00 15, 54 18, 00 13, 01 1, 60 23, 63 7, 00 18, 58 12, 00 14, 54 18, 10 13, 75 1, 70 23, 86 7, 10 17, 18 12, 10 12, 96 19, 00 7, 76 1, 50 25, 80 7, 00 19, 95 13, 00 16, 75 19, 00 9, 38 2, 00 21, 82 7, 80 18, 65 13, 00 14, 36 20, 30 7, 35 2, 00 23, 42 8, 00 18, 12 13, 00 16, 25 21, 00 9, 57 2, 40 22, 87 8, 00 19, 17 13, 40 16, 28 22, 90 4, 96 3, 00 20, 89 8, 70 16, 29 13, 00 13, 49 23, 10 3, 34 3, 00 18, 78 8, 00 21, 12 13, 00 17, 64 24, 00 7, 68 3, 40 21, 24 8, 00 16, 61 14, 00 10, 71 24, 00 7, 25 3, 00 18, 82 8, 20 19, 54 14, 50 10, 20 25, 10 5, 37 3, 00 22, 33 8, 00 18, 44 14, 00 13, 69 25, 00 8, 31 3, 60 19, 50 9, 00 18, 44 14, 00 16, 53 25, 00 2, 94 4, 00 19, 75 9, 00 20, 61 14, 20 13, 60 25, 00 4, 40 4, 10 22, 09 9, 10 18, 68 15, 00 9, 51 26, 70 4, 93 5, 00 23, 13 9, 00 15, 28 15, 00 16, 05 26, 00 5, 94 5, 40 18, 74 9, 60 19, 04 15, 00 9, 86 26, 20 4, 24 5, 00 17, 99 10, 00 16, 42 16, 00 14, 48 27, 00 1, 29 5, 00 18, 87 10, 00 16, 13 16, 00 11, 52 28, 20 3, 87 5, 20 23, 06 10, 30 17, 10 16, 00 9, 51 28, 00 475, 92 5, 00 23, 12 10, 00 18, 63 16, 00 15, 08 29, 00 5, 05

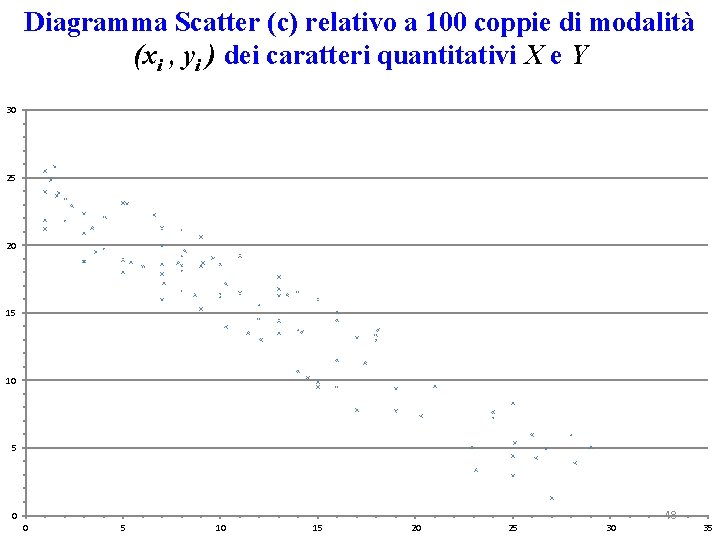
Diagramma Scatter (c) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 30 25 20 15 10 5 0 0 5 10 15 20 25 30 48 35

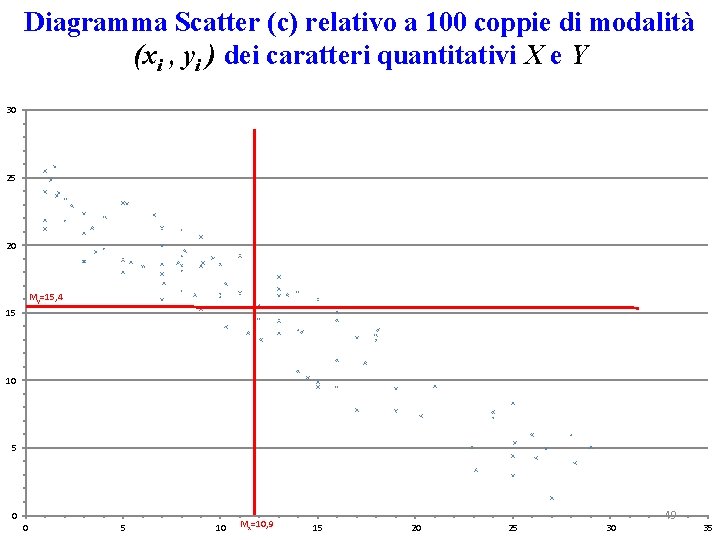
Diagramma Scatter (c) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 30 25 20 My=15, 4 15 10 5 0 0 5 10 Mx=10, 9 15 20 25 30 49 35
![Nel data set c sono prevalenti i prodotti di scarti negativi cioè xiMX Nel data set (c) sono prevalenti i prodotti di scarti negativi, cioè [(xi-M(X)] ×](https://slidetodoc.com/presentation_image_h2/5e7344ba54d9d30394a2822c45bfcb38/image-50.jpg)
Nel data set (c) sono prevalenti i prodotti di scarti negativi, cioè [(xi-M(X)] × [yi –M(Y)] < 0 (essendo i caratteri quantitativi X e Y discordi), quindi in particolare: Cov(X, Y)<0 , Cov(X, Y)= - 43, 72. ……. . -……. In caso di bilanciamento tra prodotti degli scarti positivi e negativi si ha: Cov( X , Y ) = 0.

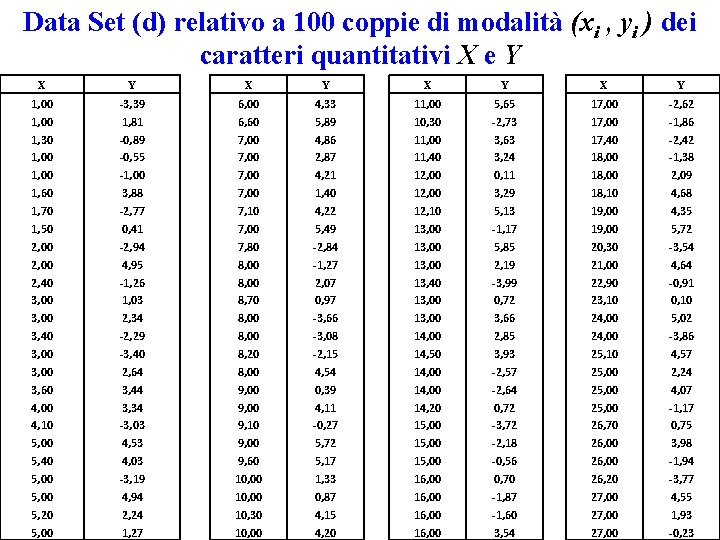
Data Set (d) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y X Y X Y 1, 00 1, 30 1, 00 1, 60 1, 70 1, 50 2, 00 2, 40 3, 00 3, 60 4, 00 4, 10 5, 00 5, 40 5, 00 5, 20 -3, 39 1, 81 -0, 89 -0, 55 -1, 00 3, 88 -2, 77 0, 41 -2, 94 4, 95 -1, 26 1, 03 2, 34 -2, 29 -3, 40 2, 64 3, 44 3, 34 -3, 03 4, 53 4, 03 -3, 19 4, 94 2, 24 6, 00 6, 60 7, 00 7, 10 7, 00 7, 80 8, 00 8, 70 8, 00 8, 20 8, 00 9, 10 9, 00 9, 60 10, 00 10, 30 4, 33 5, 89 4, 86 2, 87 4, 21 1, 40 4, 22 5, 49 -2, 84 -1, 27 2, 07 0, 97 -3, 66 -3, 08 -2, 15 4, 54 0, 39 4, 11 -0, 27 5, 72 5, 17 1, 33 0, 87 4, 15 11, 00 10, 30 11, 00 11, 40 12, 00 12, 10 13, 00 13, 40 13, 00 14, 50 14, 00 14, 20 15, 00 16, 00 5, 65 -2, 73 3, 63 3, 24 0, 11 3, 29 5, 13 -1, 17 5, 85 2, 19 -3, 99 0, 72 3, 66 2, 85 3, 93 -2, 57 -2, 64 0, 72 -3, 72 -2, 18 -0, 56 0, 70 -1, 87 -1, 60 17, 00 17, 40 18, 00 18, 10 19, 00 20, 30 21, 00 22, 90 23, 10 24, 00 25, 10 25, 00 26, 70 26, 00 26, 20 27, 00 -2, 62 -1, 86 -2, 42 -1, 38 2, 09 4, 68 4, 35 5, 72 -3, 54 4, 64 -0, 91 0, 10 5, 02 -3, 86 4, 57 2, 24 4, 07 -1, 17 0, 75 3, 98 -1, 94 -3, 77 4, 55 1, 93 5, 00 1, 27 10, 00 4, 20 16, 00 3, 54 27, 00 -0, 23

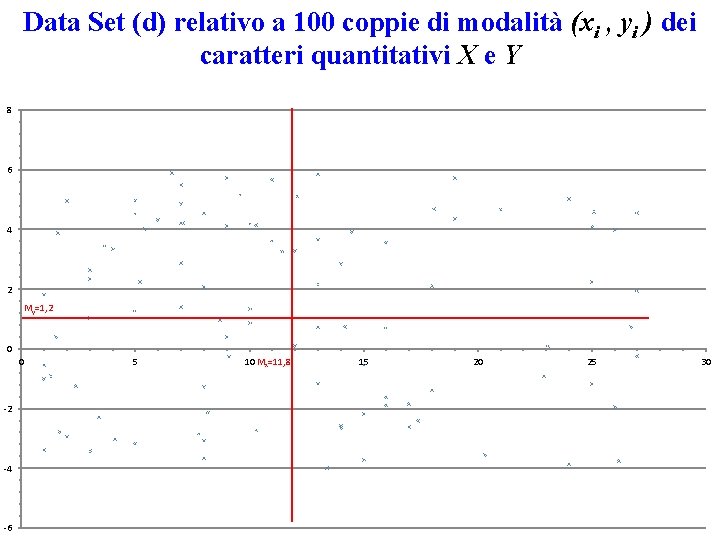
Data Set (d) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 8 6 4 2 My=1, 2 0 0 -2 -4 -6 5 10 Mx=11, 8 15 20 25 30

Nel data set (d) i prodotti di scarti positivi equivalgono quelli negativi, non solo, ma a valori di X piccoli corrispondono sia valori di Y piccoli che grandi e lo stesso succede per i valori grandi di X. In altre parole, non si riesce a riconoscere alcuna relazione funzionale tra i valori di Y in funzione di X (ma anche viceversa). In questa situazione se in una unità si conosce la modalità con la quale si manifesta uno dei due caratteri è impossibile fare una previsione razionale circa la modalità del secondo carattere. Per cui concluderemo che: X ed Y sono INDIPENDENTI In particolare, in questo data set (d) si ha: Cov(X, Y)= - 0, 20.

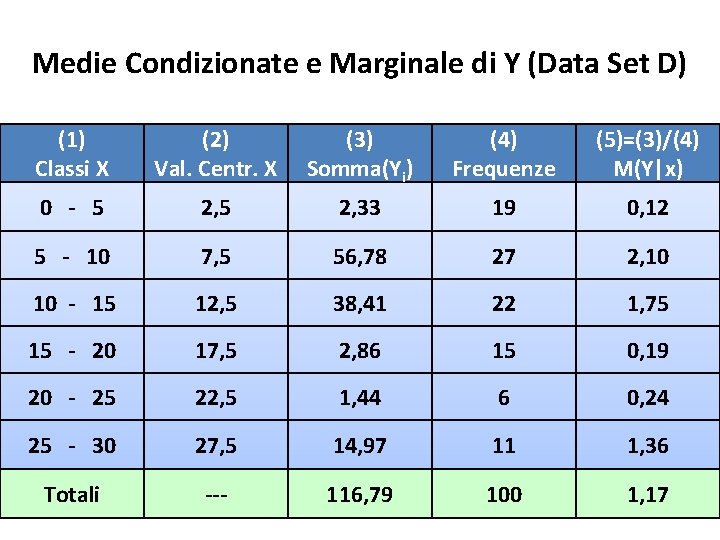
Medie Condizionate e Marginale di Y (Data Set D) (1) Classi X (2) Val. Centr. X (3) Somma(Yi) (4) Frequenze (5)=(3)/(4) M(Y|x) 0 - 5 2, 33 19 0, 12 5 - 10 7, 5 56, 78 27 2, 10 10 - 15 12, 5 38, 41 22 1, 75 15 - 20 17, 5 2, 86 15 0, 19 20 - 25 22, 5 1, 44 6 0, 24 25 - 30 27, 5 14, 97 11 1, 36 Totali --- 116, 79 100 1, 17

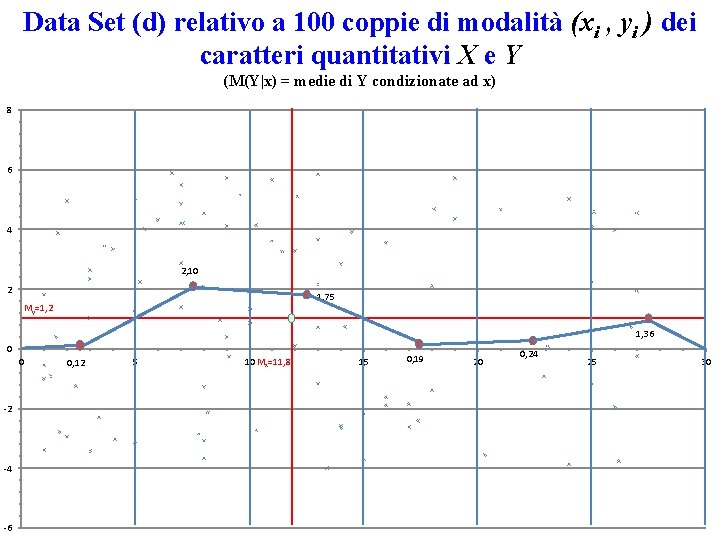
Data Set (d) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y (M(Y|x) = medie di Y condizionate ad x) 8 6 4 2, 10 2 1, 75 My=1, 2 1, 36 0 0 -2 -4 -6 0, 12 5 10 Mx=11, 8 15 0, 19 20 0, 24 25 30

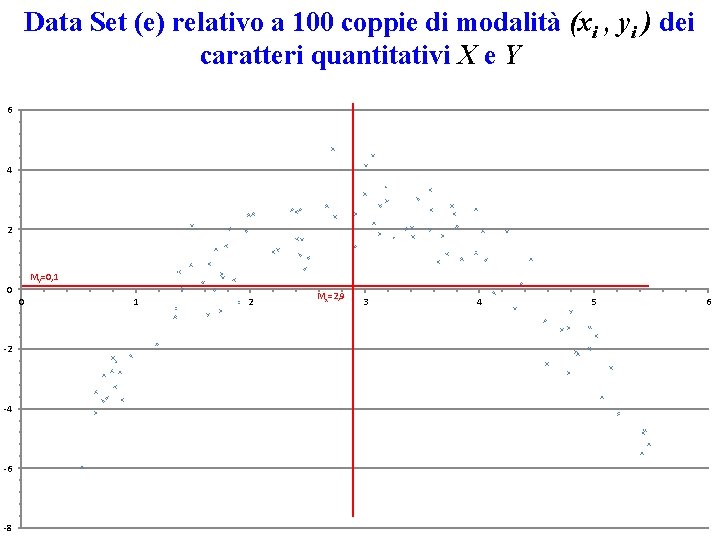
Data Set (e) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y X Y X Y 2, 24 3, 01 1, 96 1, 74 2, 74 3, 00 3, 25 3, 07 4, 31 1, 75 2, 40 4, 96 3, 46 1, 76 1, 41 3, 97 2, 91 5, 07 2, 92 5, 02 4, 84 3, 41 2, 41 3, 37 0, 65 1, 32 4, 13 1, 96 -0, 73 2, 42 3, 18 1, 73 4, 47 -0, 66 0, 51 2, 58 -2, 01 3, 03 0, 38 0, 00 1, 20 1, 40 -3, 62 2, 51 -1, 57 -2, 10 2, 06 1, 68 2, 00 0, 83 3, 13 4, 80 1, 63 3, 78 2, 67 4, 06 5, 15 3, 97 4, 78 3, 42 4, 97 3, 19 0, 80 1, 18 2, 02 0, 53 0, 88 2, 36 1, 38 3, 57 4, 13 3, 68 4, 86 -2, 45 1, 85 -0, 75 -0, 85 2, 51 2, 77 0, 99 -2, 64 2, 68 -1, 30 1, 75 -1, 26 2, 95 -2, 30 -1, 83 2, 50 -5, 97 -3, 71 2, 64 0, 57 3, 32 -0, 14 1, 77 -2, 18 4, 78 3, 80 1, 90 5, 22 2, 20 2, 50 1, 68 3, 13 5, 43 2, 43 4, 59 3, 85 0, 86 1, 34 5, 45 1, 59 3, 58 5, 48 2, 45 4, 03 0, 82 0, 75 4, 24 3, 64 -2, 80 2, 12 -0, 48 -4, 20 1, 24 1, 06 -0, 01 2, 80 -4, 82 1, 16 -2, 51 1, 00 -2, 78 -0, 95 -4, 71 0, 20 2, 65 -5, 19 1, 66 1, 94 -3, 27 -3, 63 1, 92 0, 91 4, 36 3, 57 4, 57 1, 99 1, 49 5, 42 1, 86 3, 72 1, 48 1, 81 4, 45 0, 72 3, 08 2, 48 3, 76 4, 72 0, 65 0, 96 1, 79 0, 79 1, 64 2, 43 0, 71 2, 72 0, 16 1, 99 -1, 08 2, 47 2, 13 -5, 50 0, 31 1, 17 0, 80 2, 03 1, 00 -2, 88 2, 21 0, 69 2, 78 -1, 36 -4, 15 -2, 25 1, 45 -2, 75 0, 84 2, 64 -3, 73 4, 69 -3, 46 3, 18 3, 41 1, 70 1, 34 1, 35 -0, 62

Data Set (e) relativo a 100 coppie di modalità (xi , yi ) dei caratteri quantitativi X e Y 6 4 2 My=0, 1 0 0 -2 -4 -6 -8 1 2 Mx=2, 9 3 4 5 6

Anche per il data set (e) c’è un bilanciamento nei quattro quadranti, come nel caso del data set (d), quindi la covarianza, se non proprio nulla, sarà vicina a zero. Infatti in questo data set (e) si ha: Cov(X, Y)= - 0, 03. Rispetto al data set (d), i punti del diagramma scatter relativo al data set (e) mostrano, però, una chiara relazione funzionale di Y rispetto alla X. In particolare, al crescere della X la Y prima cresce e poi decresce. Pertanto, in una unità, conoscendo la modalità di X adesso siamo in grado di poter fare una previsione sul valore della Y, quindi possiamo concludere che Y DIPENDE da X, anche se la dipendenza non è LINEARE, cioè la CORRELAZIONE è quasi NULLA.

Da tutto quello è stato mostrato negli esempi si evince chiaramente che: se tra i due caratteri X ed Y c’è perfetta INDIPENDENZA allora la COVARIANZA è pari a zero. Non vale il viceversa, cioè: se la COVARIANZA è nulla non è detto che i due caratteri X ed Y siano INDIPENDENTI perché Y potrebbe essere legata ad X da una relazione diversa da quella lineare. In altre parole: se c’è INDIPENDENZA c’è (a fortiori) INCORRELAZIONE, se c’è INCORRELAZIONE non è detto che ci sia INDIPENDENZA. In simboli: Indipendenza � Cov(X, Y)=0

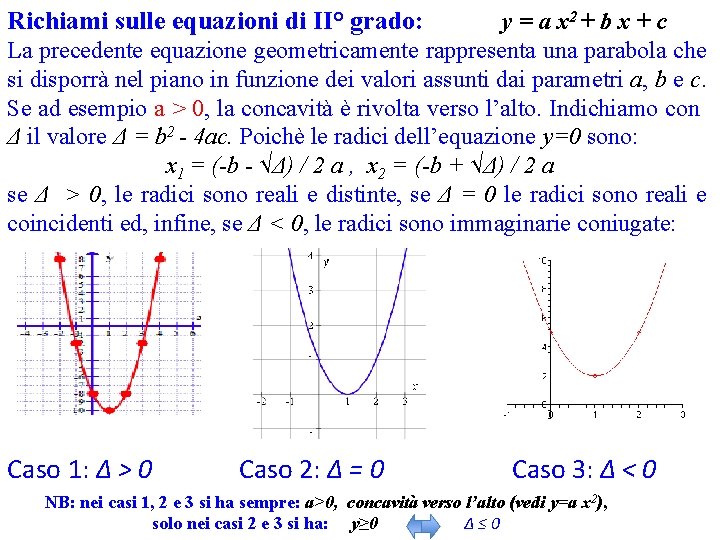
Richiami sulle equazioni di II° grado: y = a x 2 + b x + c La precedente equazione geometricamente rappresenta una parabola che si disporrà nel piano in funzione dei valori assunti dai parametri a, b e c. Se ad esempio a > 0, la concavità è rivolta verso l’alto. Indichiamo con Δ il valore Δ = b 2 - 4 ac. Poichè le radici dell’equazione y=0 sono: x 1 = (-b - √Δ) / 2 a , x 2 = (-b + √Δ) / 2 a se Δ > 0, le radici sono reali e distinte, se Δ = 0 le radici sono reali e coincidenti ed, infine, se Δ < 0, le radici sono immaginarie coniugate: Caso 1: Δ > 0 Caso 2: Δ = 0 Caso 3: Δ < 0 NB: nei casi 1, 2 e 3 si ha sempre: a>0, concavità verso l’alto (vedi y=a x 2), solo nei casi 2 e 3 si ha: y≥ 0 Δ≤ 0

Diseguaglianza di Cauchy-Schwarz Cov( X , Y )2 ≤ V( X ) V( Y ) Dimostrazione: Cioè: 61

Poiché l’espressione precedente è non – negativa, cioè si ha sempre y ≥ 0 ed a > 0, quindi il polinomio in l, (a) (b) (c) non ammette radici reali e distinte, cioè il suo discriminante Δ è Δ ≤ 0 (perché y ≥ 0) , cioè: 62

ma, sostituendo al posto di zi e wi gli scarti di xi e yi dalle rispettive medie, avremo: cioè: Cov( X , Y )2 ≤ V( X ) V( Y ) c. d. d. da cui consegue: 63

Nella diseguaglianza di Cauchy-Schwarz vale il segno “=“ quando X ed Y sono legate da una perfetta relazione lineare, cioè Y=a+b. X. Infatti, se Y=a+b. X allora yi = a + b xi , quindi, ricordando che M(Y) = a + b M(X), avremo: 64

inoltre, essendoci una relazione lineare tra le medie avremo anche: M(X)=-(a/b)+M(Y)/b pertanto: 65

quindi, in ultima analisi: Cov(X, Y)=b. V(X) Cov(X, Y)=V(Y)/b pertanto se: Y=a+b. X allora Cov(X, Y)2=V(X)V(Y) c. d. d. inoltre, se b>0 si ha Cov(X, Y)=b. V(X)≥ 0 , quindi: se, invece, b<0 si ha Cov(X, Y)=b. V(X)≤ 0 , quindi: 66

Indice relativo di dipendenza lineare o correlazione: il significato di r(X, Y), detto coefficiente di correlazione di Bravais – Pearson, è identico a quello di Cov(X, Y) ma, a differenza di quest’ultima, r(X, Y) è una misura relativa di correlazione. 67

Per il Data Set (a) avremo: M(X)=11, 87; M(Y)=9, 87; V(X)=58, 74; V(Y)=102, 84; Cov(X, Y)=41, 42; r(X, Y)=0, 53. Per il data set (b) avremo: M(X)=11, 87; M(Y)=10, 29; V(X)=58, 78; V(Y)=33, 21; Cov(X, Y)=41, 64; r(X, Y)=0, 94. Per il data set (c) avremo: M(X)=11, 88; M(Y)=15, 40; V(X)=59, 05; V(Y)=36, 31; Cov(X, Y)=-43, 72; r(X, Y)=-0, 94. Per il data set (d) avremo: M(X)=11, 82; M(Y)=1, 17; V(X)=57, 42; V(Y)=9, 28; Cov(X, Y)=-0, 20; r(X, Y)=-0, 01. Per il data set (e) avremo: M(X)=2, 91; M(Y)=0, 14; V(X)=2, 01; V(Y)=6, 17; Cov(X, Y)=-0, 03; r(X, Y)=-0, 01. 68


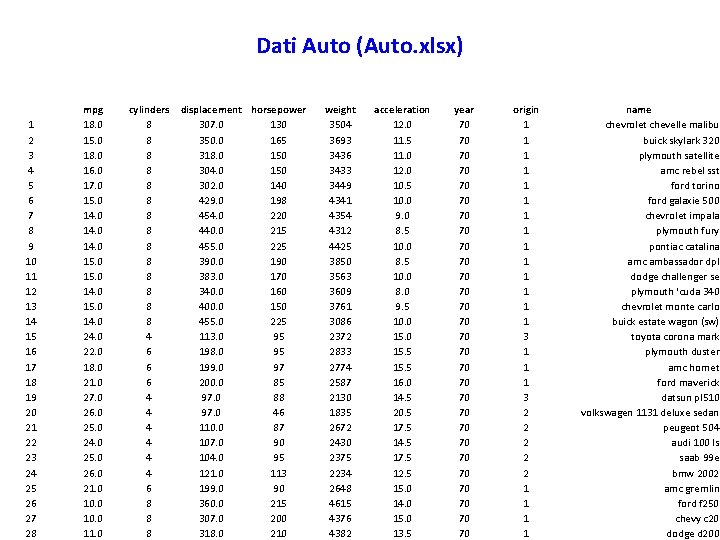
Dati Auto (Auto. xlsx) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 mpg 18. 0 15. 0 18. 0 16. 0 17. 0 15. 0 14. 0 22. 0 18. 0 21. 0 27. 0 26. 0 25. 0 24. 0 25. 0 26. 0 21. 0 10. 0 11. 0 cylinders displacement horsepower 8 307. 0 130 8 350. 0 165 8 318. 0 150 8 304. 0 150 8 302. 0 140 8 429. 0 198 8 454. 0 220 8 440. 0 215 8 455. 0 225 8 390. 0 190 8 383. 0 170 8 340. 0 160 8 400. 0 150 8 455. 0 225 4 113. 0 95 6 198. 0 95 6 199. 0 97 6 200. 0 85 4 97. 0 88 4 97. 0 46 4 110. 0 87 4 107. 0 90 4 104. 0 95 4 121. 0 113 6 199. 0 90 8 360. 0 215 8 307. 0 200 8 318. 0 210 weight 3504 3693 3436 3433 3449 4341 4354 4312 4425 3850 3563 3609 3761 3086 2372 2833 2774 2587 2130 1835 2672 2430 2375 2234 2648 4615 4376 4382 acceleration 12. 0 11. 5 11. 0 12. 0 10. 5 10. 0 9. 0 8. 5 10. 0 8. 0 9. 5 10. 0 15. 5 16. 0 14. 5 20. 5 17. 5 14. 5 17. 5 12. 5 15. 0 14. 0 15. 0 13. 5 year 70 70 70 70 70 70 70 origin 1 1 1 1 3 1 1 1 3 2 2 2 1 1 name chevrolet chevelle malibu buick skylark 320 plymouth satellite amc rebel sst ford torino ford galaxie 500 chevrolet impala plymouth fury pontiac catalina amc ambassador dpl dodge challenger se plymouth 'cuda 340 chevrolet monte carlo buick estate wagon (sw) toyota corona mark plymouth duster amc hornet ford maverick datsun pl 510 volkswagen 1131 deluxe sedan peugeot 504 audi 100 ls saab 99 e bmw 2002 amc gremlin ford f 250 chevy c 20 dodge d 200

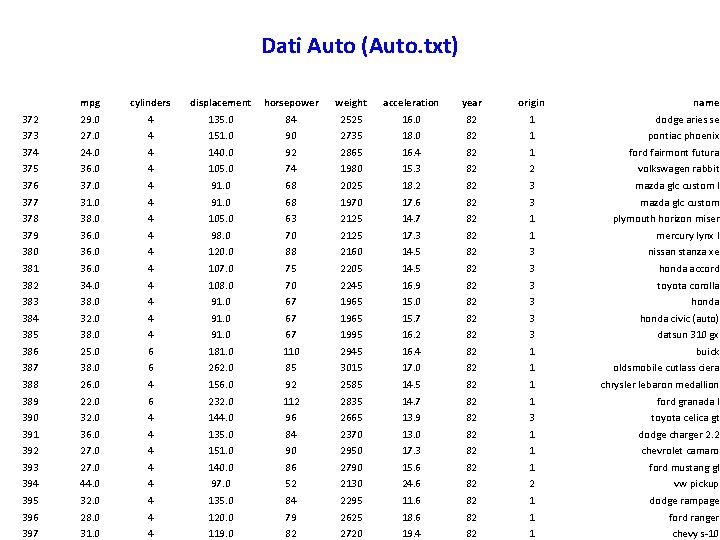
Dati Auto (Auto. txt) mpg cylinders displacement horsepower weight acceleration year origin name 372 29. 0 4 135. 0 84 2525 16. 0 82 1 dodge aries se 373 27. 0 4 151. 0 90 2735 18. 0 82 1 pontiac phoenix 374 24. 0 4 140. 0 92 2865 16. 4 82 1 ford fairmont futura 375 36. 0 4 105. 0 74 1980 15. 3 82 2 volkswagen rabbit 376 37. 0 4 91. 0 68 2025 18. 2 82 3 mazda glc custom l 377 31. 0 4 91. 0 68 1970 17. 6 82 3 mazda glc custom 378 38. 0 4 105. 0 63 2125 14. 7 82 1 plymouth horizon miser 379 36. 0 4 98. 0 70 2125 17. 3 82 1 mercury lynx l 380 36. 0 4 120. 0 88 2160 14. 5 82 3 nissan stanza xe 381 36. 0 4 107. 0 75 2205 14. 5 82 3 honda accord 382 34. 0 4 108. 0 70 2245 16. 9 82 3 toyota corolla 383 38. 0 4 91. 0 67 1965 15. 0 82 3 honda 384 32. 0 4 91. 0 67 1965 15. 7 82 3 honda civic (auto) 385 38. 0 4 91. 0 67 1995 16. 2 82 3 datsun 310 gx 386 25. 0 6 181. 0 110 2945 16. 4 82 1 buick 387 38. 0 6 262. 0 85 3015 17. 0 82 1 oldsmobile cutlass ciera 388 26. 0 4 156. 0 92 2585 14. 5 82 1 chrysler lebaron medallion 389 22. 0 6 232. 0 112 2835 14. 7 82 1 ford granada l 390 32. 0 4 144. 0 96 2665 13. 9 82 3 toyota celica gt 391 36. 0 4 135. 0 84 2370 13. 0 82 1 dodge charger 2. 2 392 27. 0 4 151. 0 90 2950 17. 3 82 1 chevrolet camaro 393 27. 0 4 140. 0 86 2790 15. 6 82 1 ford mustang gl 394 44. 0 4 97. 0 52 2130 24. 6 82 2 vw pickup 395 32. 0 4 135. 0 84 2295 11. 6 82 1 dodge rampage 396 28. 0 4 120. 0 79 2625 18. 6 82 1 ford ranger 397 31. 0 4 119. 0 82 2720 19. 4 82 1 chevy s-10

Diagrammi di Dispersione per coppie di variabili (dati Auto. txt)

Sino ad ora, nello studio dei delle distribuzioni bivariate abbiamo supposto che i dati siano forniti sotto forma di n coppie di modalità rilevate (xi , yi ). Analizzeremo ora il caso in cui, invece, essi siano forniti sotto forma di: tabella a doppia entrata o tabella di contingenza. I dati da prendere in considerazione saranno ora le r x s coppie (xi , yj ) di modalità diverse ciascuna considerata con la propria frequenza nij. 73

Tabella a Doppia Entrata La covarianza rimane definita come la media aritmetica, in questo caso “ponderata”, dei prodotti degli scarti dalla media, 74 rispettivamente, di X e di Y.

Si noti che se le variabili X e Y sono indipendenti allora si avrà che: nij = ni. n. j / n , (i, j), sostituendo nella formula della covarianza avremo: =0 0=0 In conclusione: se (X, Y) sono Indipendenti Cov(X, Y)=0 , r(X, Y)=0. NON E’ VERO IL VICEVERSA 75

Calcolo semplificato della Covarianza da cui: 76

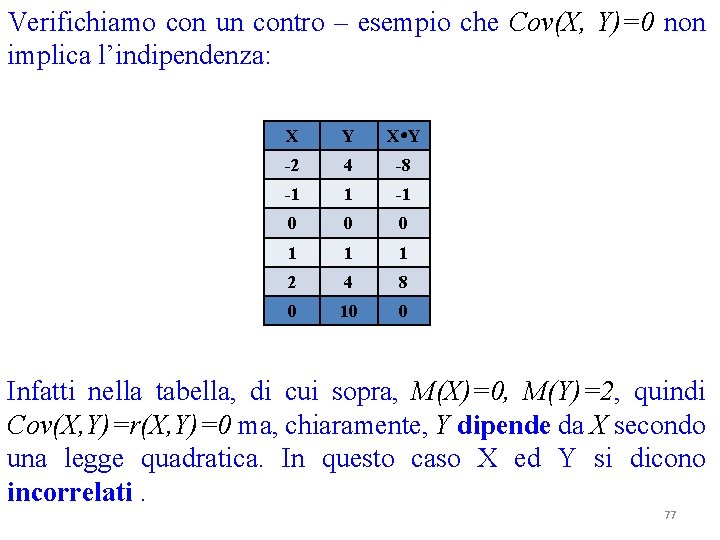
Verifichiamo con un contro – esempio che Cov(X, Y)=0 non implica l’indipendenza: X Y -2 4 -8 -1 1 -1 0 0 0 1 1 1 2 4 8 0 10 0 Infatti nella tabella, di cui sopra, M(X)=0, M(Y)=2, quindi Cov(X, Y)=r(X, Y)=0 ma, chiaramente, Y dipende da X secondo una legge quadratica. In questo caso X ed Y si dicono incorrelati. 77

se i dati sono organizzati in una tabella a doppia entrata avremo analogamente: il calcolo del coefficiente di correlazione si effettuerà come di consueto: 78
 Indipendenza lineare
Indipendenza lineare Definizioni geometria piana
Definizioni geometria piana Formule geometria piana
Formule geometria piana Cerchio definizione
Cerchio definizione Distanza tra due ounti
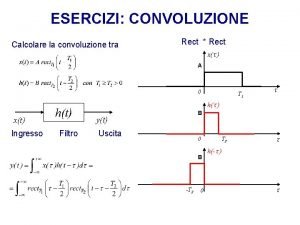
Distanza tra due ounti Esercizi convoluzione
Esercizi convoluzione Architettura tra le due guerre
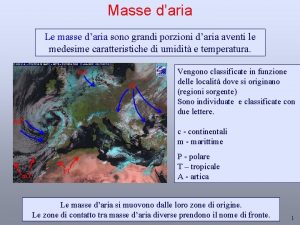
Architettura tra le due guerre Confine tra due masse d'aria
Confine tra due masse d'aria Rette perpendicolari
Rette perpendicolari Profilo egiziano
Profilo egiziano Distanza tra due punti sulla stessa retta
Distanza tra due punti sulla stessa retta La relazione d'aiuto slide
La relazione d'aiuto slide Mappa piano cartesiano
Mappa piano cartesiano Rapporto tra due aree con notazione scientifica
Rapporto tra due aree con notazione scientifica Unione tra due insiemi
Unione tra due insiemi Funzione di proporzionalità quadratica
Funzione di proporzionalità quadratica Il concetto di rapporto
Il concetto di rapporto Geometria ammoniaca
Geometria ammoniaca Rapporto di due numeri
Rapporto di due numeri La differenza tra due angoli complementari è di 24
La differenza tra due angoli complementari è di 24 Ha quattro lati uguali
Ha quattro lati uguali Substantive vs procedural due process
Substantive vs procedural due process Slidetodoc. com
Slidetodoc. com Principio di conservazione della quantità di moto
Principio di conservazione della quantità di moto I gradi della proposizione subordinata
I gradi della proposizione subordinata Linvenzione della stampa
Linvenzione della stampa Interpretazione delle norme giuridiche mappa concettuale
Interpretazione delle norme giuridiche mappa concettuale Avanguardie artistiche del 900
Avanguardie artistiche del 900 Caratteri dell'ellenismo
Caratteri dell'ellenismo Caratteristiche del positivismo
Caratteristiche del positivismo Caratteri generali dell'impressionismo
Caratteri generali dell'impressionismo Caratteri tipografici giambattista
Caratteri tipografici giambattista Caratteristiche del genere epico
Caratteristiche del genere epico Caratteristiche norma giuridica
Caratteristiche norma giuridica Caratteri ereditari esempi
Caratteri ereditari esempi Polsi periferici
Polsi periferici Post impressionismo caratteri generali
Post impressionismo caratteri generali Caratteri generali del barocco
Caratteri generali del barocco Famiglia reale inglese albero genealogico
Famiglia reale inglese albero genealogico Postimpressionismo caratteristiche
Postimpressionismo caratteristiche Caratteri lapidari
Caratteri lapidari Caratteri generali del romanticismo
Caratteri generali del romanticismo Esempi di norme religiose
Esempi di norme religiose Caratteri mendeliani
Caratteri mendeliani Romanticismo caratteri generali
Romanticismo caratteri generali Sexo toluca tra
Sexo toluca tra Quale fu il rapporto tra i tiranni è il demos
Quale fu il rapporto tra i tiranni è il demos Brandtermostat honeywell
Brandtermostat honeywell Kim tra
Kim tra Equazione di 2 grado esercizi
Equazione di 2 grado esercizi Tra bài
Tra bài Regola della divisione
Regola della divisione Tra bài
Tra bài Slidetodoc.com
Slidetodoc.com Differenza tra mandato e protettorato
Differenza tra mandato e protettorato Architettura cisc
Architettura cisc Sammansatta sockerarter
Sammansatta sockerarter Complemento oggetto
Complemento oggetto Chọn câu trả lời
Chọn câu trả lời Wanax miceneo
Wanax miceneo Prima declinazione greco alfa impuro
Prima declinazione greco alfa impuro Strofa 8 versi
Strofa 8 versi Tabella verbi da completare
Tabella verbi da completare Equazioni con le frazioni
Equazioni con le frazioni Addizioni tra polinomi
Addizioni tra polinomi Distanza tra rette
Distanza tra rette Pr��ca na ministerstve kult��ry
Pr��ca na ministerstve kult��ry Differenza tra classe e oggetto
Differenza tra classe e oggetto Ideogramma matematica
Ideogramma matematica Un poeta tra i precursori dello stilnovo
Un poeta tra i precursori dello stilnovo Risoluzione contratto
Risoluzione contratto Differenza tra cgm e fgm
Differenza tra cgm e fgm Tra bong vietnam
Tra bong vietnam Urto elastico
Urto elastico Kim tra
Kim tra Le forze endogene ed esogene
Le forze endogene ed esogene Competenze chiave europee
Competenze chiave europee Differenza tra sistema informatico e informativo
Differenza tra sistema informatico e informativo Dialogo nella coppia
Dialogo nella coppia