Indexing the Positions of Continuously Moving Objects Saltenis

Indexing the Positions of Continuously Moving Objects Saltenis, Jensen, Leutenegger and Lopez April 3 rd 2002 Indexing Moving Objects

Applications Mobile phones -> wireless internet terminals l Location aware service can be provided -> improvement in Qo. S l Vehicle navigation l Monitoring positions of air, sea or land based equipments l – Airplanes, boats, trucks, … April 3 rd 2002 Indexing Moving Objects 2

Conventional Approach Data assumed constant - modification explicit l Capture Continuous movement l – Very frequent updates – Outdated, inaccurate data l Requirement – Capture movement directly – Advancement of time ~-> necessary explicit updates l Solution – Object’s position –function of time and store – Updates(explicit) – function parameters changes April 3 rd 2002 Indexing Moving Objects 3

Indexing of history Indexing current and anticipated future positions (focus) l ü – Approach l – l l April 3 rd 2002 Time-Parameterized R-tree(TPR-tree) Index functional indefinitely – optimized for specific time horizondeteriorates as time progresses TPR , Bounding rectangles and the moving points are functions of time Intuitively – bounding rectangles follow moving points or other rectangles as they move Indexing Moving Objects 4

Problem Setting l Object’s position at time t : X(t) =(x 1(t), x 2(t), …. . xd(t)) – Position modeled as a linear fn of time – 2 params – 1 st : position of object at tref i. e. X(tref) – 2 nd : Velocity of the object V = (v 1, v 2, …. vd) X(t)=X(tref) + V(tref) – Modeling as fn of time enables future prediction and solves frequent update problem – Objects report positions and velocity vectors when they deviate from the current value (db value) by certain threshold April 3 rd 2002 Indexing Moving Objects 5

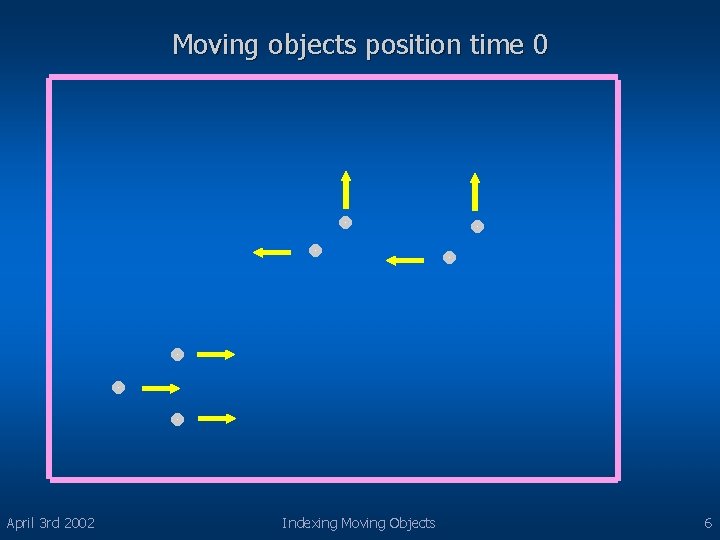
Moving objects position time 0 April 3 rd 2002 Indexing Moving Objects 6

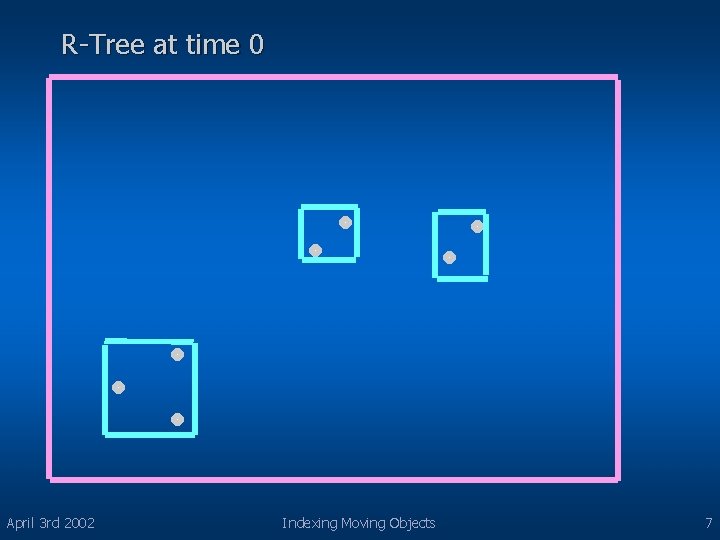
R-Tree at time 0 April 3 rd 2002 Indexing Moving Objects 7

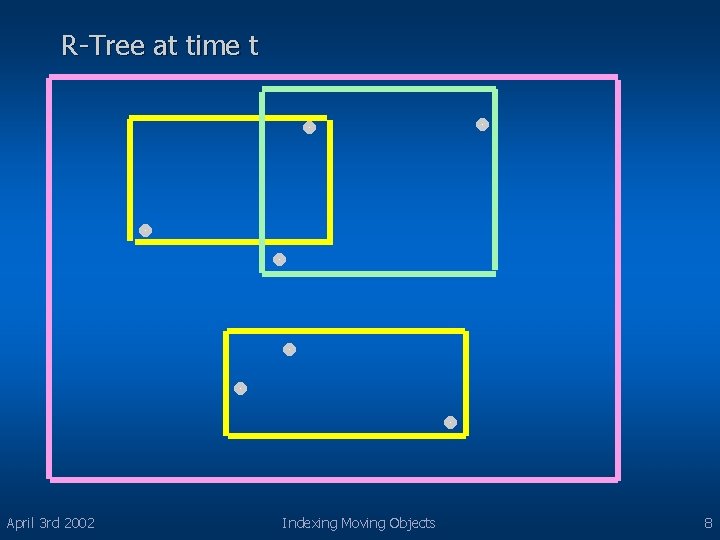
R-Tree at time t April 3 rd 2002 Indexing Moving Objects 8

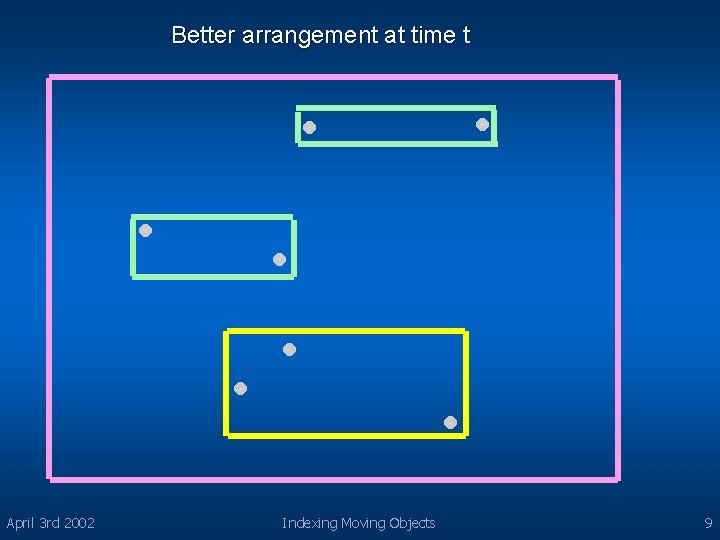
Better arrangement at time t April 3 rd 2002 Indexing Moving Objects 9

Assignment l From perspective of queries at time t, the last assignment of objects to MBRs is better – This yields worst performance @ time 0 l Assignment of objects to MBRs must take into a/c when most queries will arrive April 3 rd 2002 Indexing Moving Objects 10

Query types Retrieve all points with positions within specified regions. l d-dimensional rectangle R spec d projections l – [a 1|-, a 1 -|], …. [ad|-, ad-|] R, R 1, R 2 all d-dimensional rectangles l t, t |- < t -| 3 time values not less than current time l April 3 rd 2002 Indexing Moving Objects 11

Queries(contd) Time Slice query : Q = (R, t) specifies a hyper rectangle R located at time point t Ø Window query : Q=(R, t|-, t-|) specifies a hyper rectangle R that covers [t|-, t-|] Ø v Retrieves all points with trajectories crossing (d+1) hyper rectangle (a 1|-, a 1 -|), …, (ad|-, ad-|), [t|-, t-|] Ø Moving query : Q=(R 1, R 2, t|-, t-|) specifies the (d+1) dimensional trapezoid obtained by connecting R 1 at time t|- to R 2 at time t-| Window query generalises timeslice query l Moving query generalises window query l April 3 rd 2002 Indexing Moving Objects 12

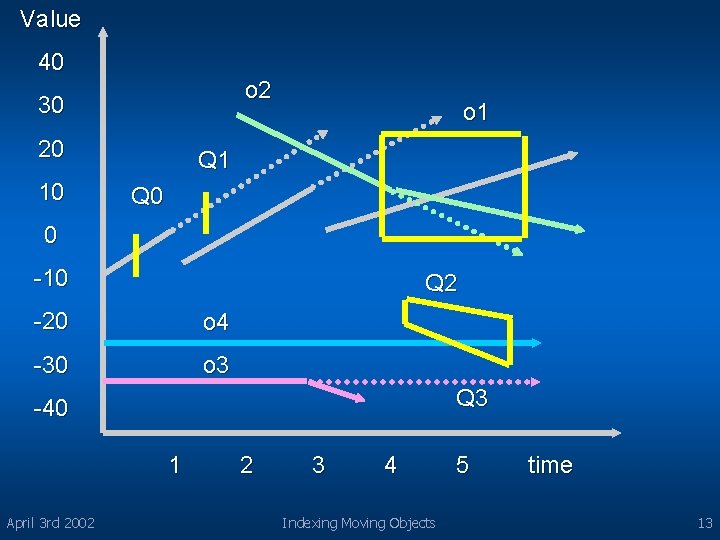
Value 40 o 2 30 20 10 o 1 Q 0 0 -10 Q 2 -20 o 4 -30 o 3 Q 3 -40 1 April 3 rd 2002 2 3 4 Indexing Moving Objects 5 time 13

Query examples Q 0 and Q 1 are timeslice queries l Q 2 is window query and Q 3 moving query l Iss(Q) – time when query issued l – Ref position and velocity depend on issue(Q) because objects update their parameters as time goes l O 1 : movement desc by 1 trajectory for iss(Q) < 1 – Another for 1<= iss(Q) < 3 and another for iss(Q) >= 3 Answer to query Q 1 is o 1 if iss(Q 1) < 1 and none if iss(Q 1) >1 l Queries in far future little value because positions predicted less accurate l Real World – expect queries concentrated in some limited time window extending from current time l April 3 rd 2002 Indexing Moving Objects 14

Problem Parameters 3 params affect indexing problem and qualities of TPR-tree l Querying window(W) : how far queries can look into the future l – Iss(Q) <= t <= Iss(Q) + W for timeslice queries – Iss(Q) <= t |- <= t -| <= Iss(Q) + W for other queries l Index Usage Time(U) : time interval during which an index will be used for querying – tl <= Iss(Q) <= tl + U tl index creation time l Time Horizon(H) : length of the time interval from which t, t |-, t -| are drawn – Time horizon for an index is index usage time plus the querying window April 3 rd 2002 Indexing Moving Objects 15

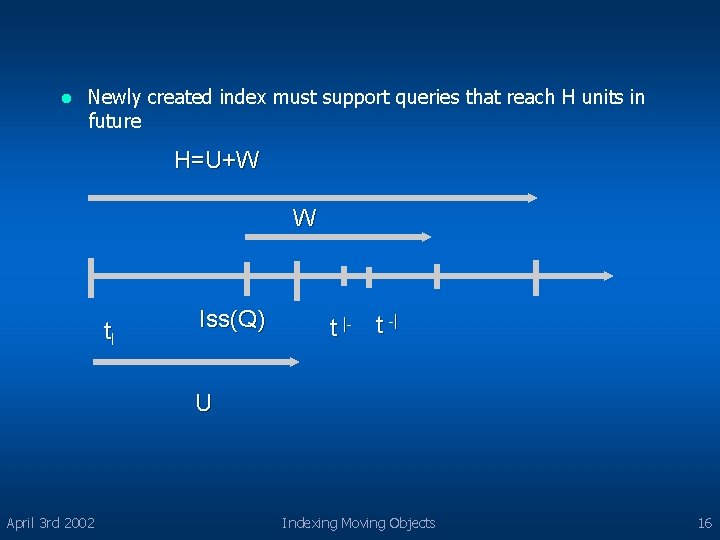
l Newly created index must support queries that reach H units in future H=U+W W tl Iss(Q) t |- t -| U April 3 rd 2002 Indexing Moving Objects 16

Index Structure TPR tree is a balanced, multi way tree with structure of an Rtree l Leaf nodes – pairs of positions of a moving point and a pointer to the moving point l Internal nodes – pairs of pointer to subtree and a rectangle that bounds the positions of all moving points or other bounding rectangles in subtree l Time parameterized d-dimensional bounding rectangles bound d -dimensional moving points or rectangles at all time not earlier than current time l April 3 rd 2002 Indexing Moving Objects 17

Conservative bounding rectangles Min at some time but possibly not at later times l In 1 d case lower bound of a conservative interval is set to move with the minimum speed of the enclosed points , upper bounds move with max speed of enclosed points l – Speeds +ve or –ve dep on direction Conservative bounding intervals never shrink l Constant size when all points have same velocity vector l – It may move April 3 rd 2002 Indexing Moving Objects 18

Querying l A bounding interval (x |-, x -|, v |-, v -|) satisfies a query (([a |-, a -|]), tq) iff – a|- <= x l -| + v -|(tq – tl) ^ a-| >= x |- + v|-(tq-tl) To answer window queries and moving queries we need to check if in (X, t) space the trapezoid of a query intersects with the trapezoid of a bounding rectangle that is b/n the start and end times of the query – Generic polyhedron-polyhedron intersection tests may be used April 3 rd 2002 Indexing Moving Objects 19