Independent samples Wilcoxon rank sum test Example n

Independent samples. Wilcoxon rank sum test

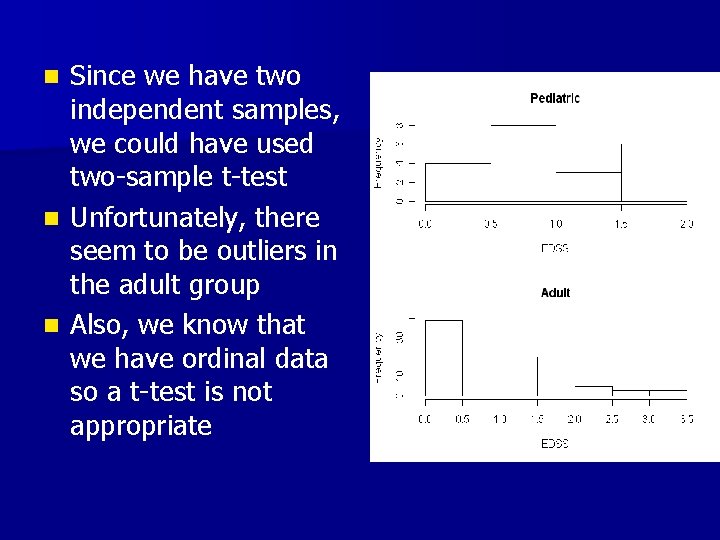
Example n n n The main outcome measure in MS is the expanded disability status scale (EDSS) The EDSS is a 0 -10 scale with steps of 0. 5 Ordinal scale – Ordered, but magnitude between steps is uncertain n Dr. Kurtzke who developed the scale believes the steps of scale are just a rank, not a measure of magnitude – This makes a t-test inappropriate

Pediatric vs. adult n Most MS patients develop the disease between age 20 -40, but a subset of patients develop MS younger n What is different about these patients? n If we investigated patients at similar disease duration, is there a significant difference in EDSS?

Since we have two independent samples, we could have used two-sample t-test n Unfortunately, there seem to be outliers in the adult group n Also, we know that we have ordinal data so a t-test is not appropriate n

Wilcoxon rank sum test Since we have two independent samples and the t-test is not appropriate, we need a nonparametric test. The test for two independent samples is Wilcoxon rank sum. n Again, we are interested in the median rather than the mean. n The hypothesis test of interest is n – H 0: medianadult = medianpediatric – HA: medianadult != medianpediatric

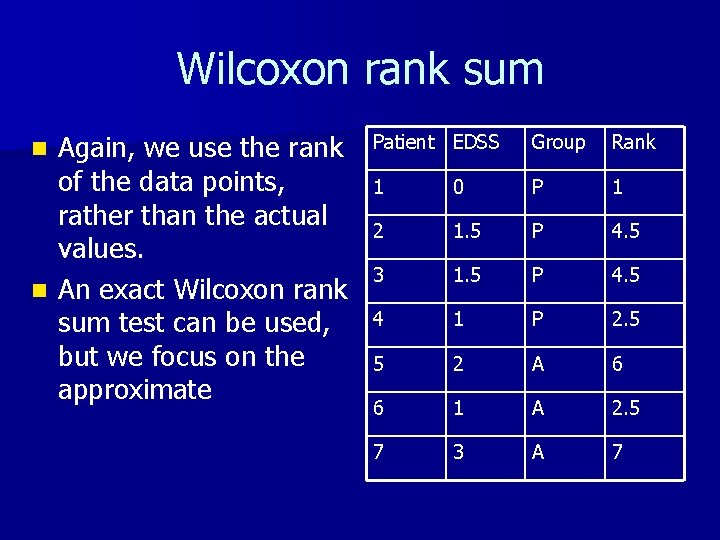
Wilcoxon rank sum Again, we use the rank of the data points, rather than the actual values. n An exact Wilcoxon rank sum test can be used, but we focus on the approximate n Patient EDSS Group Rank 1 0 P 1 2 1. 5 P 4. 5 3 1. 5 P 4. 5 4 1 P 2. 5 5 2 A 6 6 1 A 2. 5 7 3 A 7

Approximate Wilcoxon test n If the sample size is large enough (rule of thumb, n=20) an approximate Wilcoxon test based on the normal approximation can be used – W=sum of ranks in smaller group – m. W =expected sum of ranks in smaller group under null – s. W =standard deviation of sum of ranks in smaller group under null

m. T and s. T n Under the null of no difference between the groups, this expression is the expected sum of ranks in the small group n The standard deviation is given by this formula

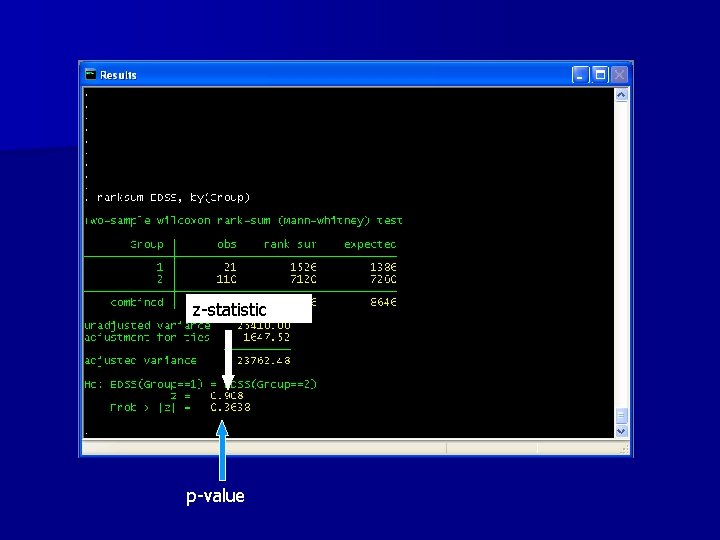
Results n From our results, – sum of the ranks in smaller group: W=1526 – expected value of sum of positive ranks: – Standard deviation of sum of positive ranks n Our approximate test statistic is

Ties n In this example, we have many ties n As with the Wilcoxon signed rank test, a correction for ties can be made to the variance (see Rosner or other text book) n This correction is included in STATA and all other computer packages

Hypothesis test 1) 2) 3) 4) 5) 6) 7) H 0: median difference=0 Continuous outcome from paired data Wilcoxon signed rank test Test statistic: z=0. 91 p-value= 0. 36 Since the p-value is more than 0. 05, we fail to reject the null hypothesis We conclude that there is no significant difference in terms of EDSS in pediatric and adult MS patients

z-statistic p-value

Comments n Wilcoxon rank sum test is becoming more prominent because computers allow this statistic to be calculated very quickly n There is not a large loss of power in using a Wilcoxon rank sum test compared to a ttest even when the normality assumption holds. n If normality does not hold or ordinal data, Wilcoxon test is better

Parametric tests-nonparametric equivalent n Paired t-test – Wilcoxon signed rank n Two sample t-test – Wilcoxon rank sum n ANOVA – Kruskal-Wallis test – When you have two or more independent samples and the assumptions of ANOVA are not met, you can use the Kruskal-Wallis test. This is a rank based test.