Independent Component Analysis ICA and Factor Analysis FA




























- Slides: 28

Independent Component Analysis (ICA) and Factor Analysis (FA) Amit Agrawal Sep 10, 2003 ENEE 698 A Seminar 1

Outline • • • Motivation for ICA Definitions, restrictions and ambiguities Comparison of ICA and FA with PCA Estimation Techniques Applications Conclusions Sep 10, 2003 ENEE 698 A Seminar 2

Motivation • Method for finding underlying components from multi-dimensional data • Focus is on Independent and Non-Gaussian components in ICA as compared to uncorrelated and gaussian components in FA and PCA Sep 10, 2003 ENEE 698 A Seminar 3

Cocktail-party Problem • Multiple speakers in room (independent) • Multiple sensors receiving signals which are mixture of original signals • Estimate original source signals from mixture of received signals • Can be viewed as Blind-Source Separation as mixing parameters are not known Sep 10, 2003 ENEE 698 A Seminar 4

ICA Definition • Observe n random variables combinations of n random variables mutually independent • • which are linear which are In Matrix Notation, X = AS Assume source signals are statistically independent Estimate the mixing parameters and source signals Find a linear transformation of observed signals such that the resulting signals are as independent as possible Sep 10, 2003 ENEE 698 A Seminar 5

Restrictions and Ambiguities • Components are assumed independent • Components must have non-gaussian densities • Energies of independent components can’t be estimated • Sign Ambiguity in independent components Sep 10, 2003 ENEE 698 A Seminar 6

Gaussian and Non-Gaussian components • If some components are gaussian and some are non-gaussian. – Can estimate all non-gaussian components – Linear combination of gaussian components can be estimated. – If only one gaussian component, model can be estimated Sep 10, 2003 ENEE 698 A Seminar 7

Why Non-Gaussian Components • Uncorrelated Gaussian r. v. are independent • Orthogonal mixing matrix can’t be estimated from Gaussian r. v. • For Gaussian r. v. estimate of model is up to an orthogonal transformation • ICA can be considered as non-gaussian factor analysis Sep 10, 2003 ENEE 698 A Seminar 8

ICA vs. PCA • PCA – Find smaller set of components with reduced correlation. Based on finding uncorrelated components – Needs only second order statistics • ICA – Based on finding independent components – Needs higher order statistics Sep 10, 2003 ENEE 698 A Seminar 9

Factor Analysis • Based on a generative latent variable model – where Y is zero mean, gaussian and uncorrelated – N is zero mean gaussian noise – Elements of Y are the unobservable factors – Elements of A are called factor loadings • In practice, have a good estimated of covariance of X – Solve for A and Noise Covariance – Variables should have high loadings on a small number of factors Sep 10, 2003 ENEE 698 A Seminar 10

FA vs. PCA • PCA – Not based on generative model, although can be derived from one – Linear transformation of observed data based on variance maximization or minimum mean-square representation – Invertible, if all components are retained • FA – Based on generative model – Value of factors cannot be directly computed from observations due to noise – Rows of Matrix A (factor loadings) are NOT proportional to eigenvectors of covariance of X • Both are based on second order statistics due to the assumption of gaussianity of factors Sep 10, 2003 ENEE 698 A Seminar 11

Whitening as Preprocessing for ICA • Elements are uncorrelated and have unit variances • Decorrelation followed by scaling • Any orthogonal transformation of whitened r. v. will be white • So whitening gives components up to orthogonal transformation. • Useful as preprocessing step for ICA. • Search is restricted to orthogonal mixing matrices • Parameters reduced from Sep 10, 2003 ENEE 698 A Seminar 12

ICA Techniques • • Maximization of non-gaussianity Maximum Likelihood Estimation Minimization of Mutual Information Non-Linear Decorrelation Sep 10, 2003 ENEE 698 A Seminar 13

ICA by Maximization of nongaussianity • S is linear combination of observed signals X • By Central Limit Theorem (CLT), sum is more gaussian. So maximize non-gaussianity of mixture of observed signals • How to measure non-gaussianity – Kurtosis – Negentropy Sep 10, 2003 ENEE 698 A Seminar 14

Non-gaussianity using Kurtosis • • Kurtosis = 0 for gaussian r. v. Kurtosis < 0 sub-gaussian e. g. uniform Kurtosis > 0 super-gaussian e. g. laplacian Simple to compute Whiten observed data x to get z; z = Vx Maximize absolute value (or square) of kurtosis of w. Tz subject to ||w|| = 1 Sep 10, 2003 ENEE 698 A Seminar 15

Gradient Algorithm using Kurtosis • Start from some initial w • Compute direction in which absolute value of kurtosis of y = w. Tz is increasing • Move vector w in that direction (Gradient Descent) Sep 10, 2003 ENEE 698 A Seminar 16

Fast. ICA Algorithm • Usual problems with gradient descent such as learning rate, slow convergence • Fast. ICA is a fixed point algorithm • Main Idea – At convergence, gradient must point in direction of true w or – Use – Normalize w to unit vector after each step Sep 10, 2003 ENEE 698 A Seminar 17

Non-gaussianity using Negentropy • • • Kurtosis is sensitive to outliers. Not a robust measure Negentropy based on information-theoretic concepts Underlying Principle – Gaussian r. v. has largest entropy among all r. v. ’s of equal variance. So gaussian r. v. is most random Negentropy = H(Ygauss) – H(Y) where Ygauss is a gaussian r. v. with same variance as Y Negentropy >= 0. Is an optimal estimator of nongaussianity Computationally difficult. Require an estimate of pdf. Approximate using higher order statistics Sep 10, 2003 ENEE 698 A Seminar 18

Negentropy… – This is same as square of kurtosis if first term is zero ( for r. v. with symmetric pdf ) – Suffers from same problems as kurtosis • Generalize higher order cumulant information – Replace y^2 and y^3 by some other functions – where v is a gaussian r. v. with zero mean and unit variance and G is a non-quadratic function – Useful choices Sep 10, 2003 ENEE 698 A Seminar 19

ICA using Maximum Likelihood (ML) Estimation • Express the Likelihood as a function of parameters of model, i. e. the elements of the mixing matrix Sep 10, 2003 ENEE 698 A Seminar 20

ML estimation • But the likelihood is also a function of densities of independent components. Hence semiparametric estimation. • Estimation is easier – If prior information on densities is available. • Likelihood is a function of mixing parameters only – If the densities can be approximated by a family of densities which are specified by a limited no. of parameters Sep 10, 2003 ENEE 698 A Seminar 21

ICA by Minimizing Mutual Information • In many cases, we can’t assume that data follows ICA model • This approach doesn’t assume anything about data • ICA is viewed as a linear decomposition that minimizes the dependence measure among components or finding maximally independent components • Mutual Information >=0 and zero if and only if the variables are statistically independent Sep 10, 2003 ENEE 698 A Seminar 22

Mutual Information • Minimization of mutual information is equivalent to maximizing the sum of nongausssianities of estimates of independent components • But in maximizing sum of nongausssianities, the estimates are forced to be uncorrelated Sep 10, 2003 ENEE 698 A Seminar 23

ICA by Non-Linear Decorrelation • Independent components can be found as nonlinearly uncorrelated linear combinations • Non-Linear Correlation is defined as where f and g are two functions with at least one of them being nonlinear • Y 1 and Y 2 are independent if and only if • Assume Y 1 and Y 2 are non-linearly decorrelated i. e. • A sufficient condition for this is that Y 1 and Y 2 are independent and for one of them the non-linearity is an odd function such that has zero mean Sep 10, 2003 ENEE 698 A Seminar 24

Applications • Feature Extraction – Taking windows from signals and considering them as multidimensional signals • Medical Applications – Removing artifacts (due to muscle activity) from Electroencephalography (EEG) and MEG data in Brain Imaging – Removal of artifacts from cardio graphic signals • Telecommunications: CDMA signal model can be cast in form of a ICA model • Econometrics: Finding hidden factors in financial data Sep 10, 2003 ENEE 698 A Seminar 25

Conclusions • • General purpose technique Formulated as estimation of a generative model Problem can be simplified by whitening of data Estimated techniques include ML estimation, non -gaussianity maximization, minimization of mutual information • Can be applied in diverse fields Sep 10, 2003 ENEE 698 A Seminar 26

References • A. Hyvarinen, J. Karhunen, E. Oja, Independent Component Analysis, Wiley Interscience, 2001 • A. Hyvarinen, E. Oja, Independent Component Analysis: A tutorial, April 1999 (http: //www. cis. hut. fi/projects/ica/) Sep 10, 2003 ENEE 698 A Seminar 27

Thank You Sep 10, 2003 ENEE 698 A Seminar 28
 Pca vs ica
Pca vs ica Cocktail party problem demo
Cocktail party problem demo Ica
Ica Observed demand formula
Observed demand formula Two main clauses
Two main clauses Ica protocol
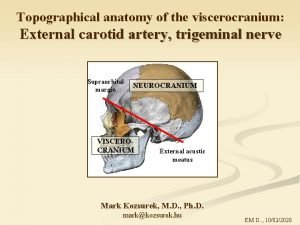
Ica protocol Internal maxillary artery branches
Internal maxillary artery branches Ica vs rdp
Ica vs rdp Indice ica
Indice ica Pca and lda
Pca and lda Pca vs ica
Pca vs ica Ica hörnan enhörna
Ica hörnan enhörna Streaming xxnx
Streaming xxnx Hotel de turistas ica
Hotel de turistas ica Ica-nsf
Ica-nsf Paraclinoid ica
Paraclinoid ica Strandzon
Strandzon ενδοθήλιο
ενδοθήλιο Organisasi ica
Organisasi ica Cocktail party problem ica
Cocktail party problem ica Ica puspita dewi anggraini
Ica puspita dewi anggraini Ica puspita dewi anggraini
Ica puspita dewi anggraini Ica puspita dewi anggraini
Ica puspita dewi anggraini Ica
Ica Validador medios ica cali
Validador medios ica cali Curso de sgso
Curso de sgso Teff ica
Teff ica Ica
Ica Pendekatan ekologi
Pendekatan ekologi