Independent and Dependent Events Slide 1 Independent Events

Independent and Dependent Events Slide 1

Independent Events Whatever happens in one event has absolutely nothing to do with what will happen next because: 1. The two events are unrelated OR 2. You repeat an event with an item whose numbers will not change (eg. : spinners or dice) OR 3. You repeat the same activity, but you REPLACE the item that was removed. The probability of two independent events, A and B, is equal to the probability of event A times the probability of event B. Slide 2

Independent Events Example: Suppose you spin each of these two spinners. What is the probability of spinning an even number and a vowel? P(even) = (3 evens out of 6 outcomes) (1 vowel out of 5 outcomes) P(vowel) = P(even, vowel) = 1 6 P S 5 2 O T 3 4 R Slide 3

Dependent Event • What happens the during the second event depends upon what happened before. • In other words, the result of the second event will change because of what happened first. The probability of two dependent events, A and B, is equal to the probability of event A times the probability of event B. However, the probability of event B now depends on event A. Slide 4

Dependent Event Example: There are 6 black pens and 8 blue pens in a jar. If you take a pen without looking and then take another pen without replacing the first, what is the probability that you will get 2 black pens? P(black first) = P(black second) = (There are 13 pens left and 5 are black) THEREFORE……………………… P(black, black) = Slide 5

TEST YOURSELF Are these dependent or independent events? 1. Tossing two dice and getting a 6 on both of them. 2. You have a bag of marbles: 3 blue, 5 white, and 12 red. You choose one marble out of the bag, look at it then put it back. Then you choose another marble. 3. You have a basket of socks. You need to find the probability of pulling out a black sock and its matching black sock without putting the first sock back. 4. You pick the letter Q from a bag containing all the letters of the alphabet. You do not put the Q back in the bag before you pick another tile. Slide 6

Independent Events Find the probability • P(jack, factor of 12) 1 5 5 x 8 5 40 = 1 8 Slide 7

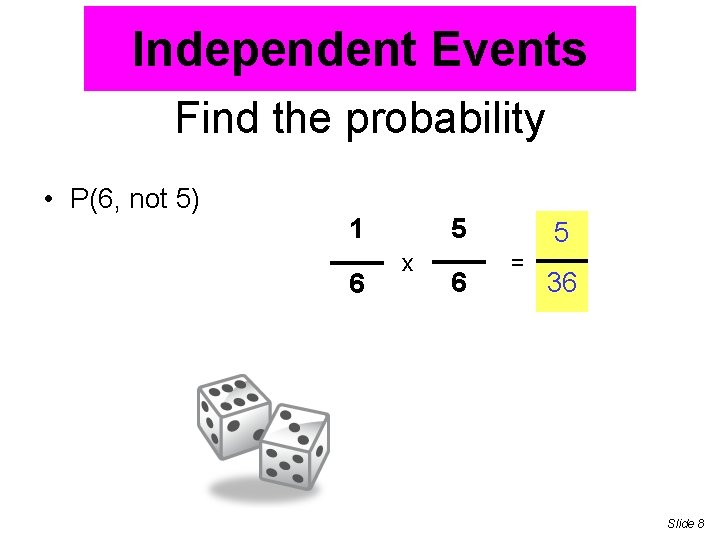
Independent Events Find the probability • P(6, not 5) 1 6 5 x 6 5 = 36 Slide 8

Dependent Events Find the probability • P(Q, Q) • All the letters of the alphabet are in the bag 1 time • Do not replace the letter 1 26 0 x 25 0 = 650 0 Slide 9