Independence and Bernoulli Trials Independence Events A and

Independence and Bernoulli Trials

Independence Events A and B are independent if § A, B independent implies: Proof for independence of are also independent. : Sharif University of Technology 2

Application Example § let : § Then § Also § Hence it follows that Ap and Aq are independent events! Sharif University of Technology 3

Some Properties of Independence The event of zero probability is independent of every other event § Let P(A)=0, § Then: § Thus: P(AB) = P(A) P(B) = 0 Other independent events cannot be ME § Since: Sharif University of Technology 4

Application Remark § A family of events {Ai} are said to be independent, if for every finite sub collection Application § If and Ais are independent, § Application in solving number theory problems. Sharif University of Technology 5

Example Three independent parallel switches Each switch remains closed with probability p. (a) Find the probability of receiving an input signal at the output. Solution § Let Ai = “Switch Si is closed” and R = “input signal is received at the output”. Then Sharif University of Technology 6

Example – continued Another Solution § Since any event and its complement form a trivial partition, § Thus: Note: The events A 1, A 2, A 3 do not form a partition, since they are not ME. Moreover, Sharif University of Technology 7

Example – continued (b) Find the probability that switch S 1 is open given that an input signal is received at the output. Solution § From Bayes’ theorem § Also, because of the symmetry : Sharif University of Technology 8

Repeated Trials § A joint performance of the two experiments with probability models ( 1, F 1, P 1) and ( 2, F 2, P 2). § Two models’ elementary events: 1, 2 § How to define the combined trio ( , F, P)? § = 1 2 § Every elementary event in is of the form = ( , ). § Events: Any subset A B of such that A F 1 and B F 2 § F : all such subsets A B together with their unions and complements. Sharif University of Technology 9

Repeated Trials § In this model, The events A 2 and 1 B are such that § Since the events A 2 and 1 B are independent for any A F 1 and B F 2. § So, for all A F 1 and B F 2 § Now, we’re done with definition of the combined model. Sharif University of Technology 10

Generalization § Experiments with § let § Elementary events § Events in are of the form and their unions and intersections. § If s are independent, and event in then is the probability of the Sharif University of Technology 11

Example § A has probability p of occurring in a single trial. § Find the probability that A occurs exactly k times, k n in n trials. Solution § The probability model for a single trial : ( , F, P) § Outcome of n experiments is : where and § A occurs at trial # i , if § Suppose A occurs exactly k times in . Sharif University of Technology 12

Example - continued § If belong to A, § Ignoring the order, this can happen in N disjoint equiprobable ways, so: § Where Sharif University of Technology 13

Bernoulli Trials § Independent repeated experiments § Outcome is either a “success” or a “failure” § The probability of k successes in n trials is given by the above formula, where p represents the probability of “success” in any one trial. Sharif University of Technology 14

Example § Toss a coin n times. Obtain the probability of getting k heads in n trials. § “head” is “success” (A) and let § Use the mentioned formula. Example § In rolling a fair dice for eight times, find the probability that either 3 or 4 shows up five times ? § Thus Sharif University of Technology 15

Bernoulli Trials § Consider a Bernoulli trial with success A, where § Let: § As § are mutually exclusive, so, Sharif University of Technology 16

Bernoulli Trials § For a given n and p what is the most likely value of k ? § Thus if or as a function of k increases until § The is the most likely number of successes in n trials. Fig. 2. 2 Sharif University of Technology 17

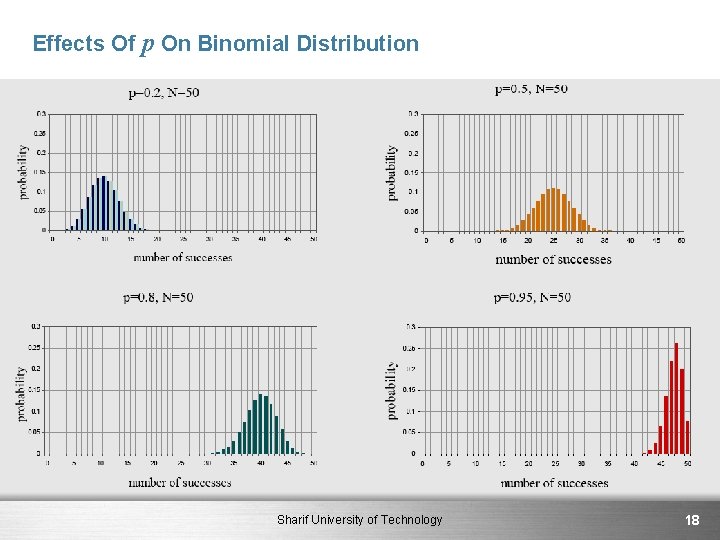
Effects Of p On Binomial Distribution Sharif University of Technology 18

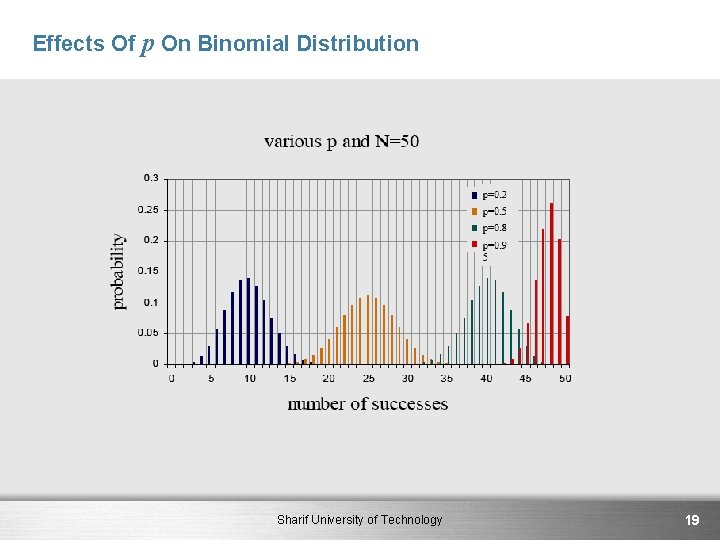
Effects Of p On Binomial Distribution Sharif University of Technology 19

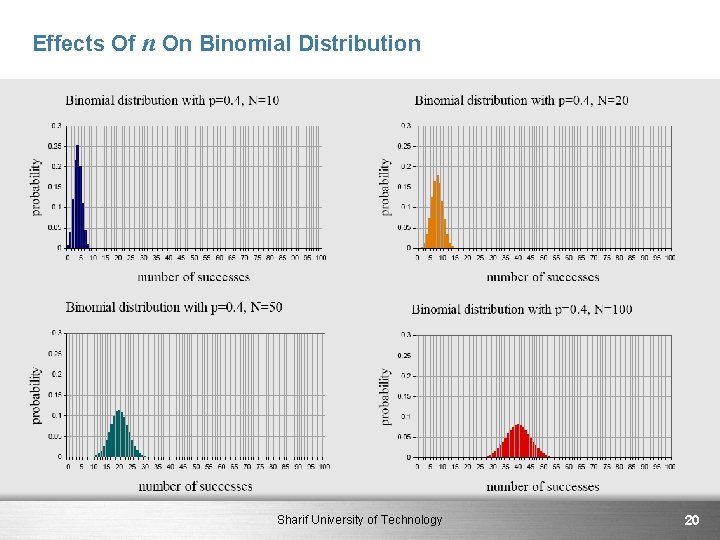
Effects Of n On Binomial Distribution Sharif University of Technology 20

Example § In a Bernoulli experiment with n trials, find the probability that the number of occurrences of A is between k 1 and k 2. Solution Sharif University of Technology 21

Example § Suppose 5, 000 components are ordered. The probability that a part is defective equals 0. 1. What is the probability that the total number of defective parts does not exceed 400 ? Solution Sharif University of Technology 22

§ If kmax is the most likely number of successes in n trials, § or § So, § This connects the results of an actual experiment to the axiomatic definition of p. Sharif University of Technology 23

Bernoulli’s Theorem § A : an event whose probability of occurrence in a single trial is p. § k : the number of occurrences of A in n independent trials § Then , § i. e. the frequency definition of probability of an event and its axiomatic definition ( p) can be made compatible to any degree of accuracy. Sharif University of Technology 24

Proof of Bernoulli’s Theorem § Direct computation gives: § Similarly, Sharif University of Technology 25

Proof of Bernoulli’s Theorem - continued § § Equivalently, § Using equations derived in the last slide, Sharif University of Technology 26

Proof of Bernoulli’s Theorem - continued § Using last two equations, Conclusion § For a given large. can be made arbitrarily small by letting n become § Relative frequency can be made arbitrarily close to the actual probability of the event A in a single trial by making the number of experiments large enough. § As the plots of tends to concentrate more and more around Sharif University of Technology 27

Example: Day-trading strategy § A box contains n randomly numbered balls (not necessarily 1 through n) § m = np (p<1) of them are drawn one by replacement § The drawing continues until a ball is drawn with a number larger than the first m numbers. § Determine the fraction p to be initially drawn, so as to maximize the probability of drawing the largest among the n numbers using this strategy. Sharif University of Technology 28

Day-trading strategy: Solution § Let drawn ball has the largest number among: all n balls, the first k balls is in the group of first m balls, k > m. § = where A = “largest among the first k balls is in the group of first m balls drawn” B = (k+1)st ball has the largest number among all n balls”. § Since A and B are independent , § So, P (“selected ball has the largest number among all balls”) Sharif University of Technology 29

Day-trading strategy: Solution § To maximize with respect to p, let: § So, p = e-1 ≈ 0. 3679 § This strategy can be used to “play the stock market”. § Suppose one gets into the market and decides to stay up to 100 days. § When to get out? § According to the solution, when the stock value exceeds the maximum among the first 37 days. § In that case the probability of hitting the top value over 100 days for the stock is also about 37%. Sharif University of Technology 30

Example: Game of Craps § A pair of dice is rolled on every play, - Win: sum of the first throw is 7 or 11 - Lose: sum of the first throw is 2, 3, 12 - Any other throw is a “carry-over” § If the first throw is a carry-over, then the player throws the dice repeatedly until: - Win: throw the same carry-over again - Lose: throw 7 Find the probability of winning the game. Sharif University of Technology 31

Game of Craps - Solution P 1: the probability of a win on the first throw Q 1: the probability of loss on the first throw B: winning the game by throwing the carry-over C: throwing the carry-over Sharif University of Technology 32

Game of Craps - Solution The probability of win by throwing the number of Plays that do not count is: The probability that the player throws the carry-over k on the j-th throw is: Sharif University of Technology 33

Game of Craps - Solution the probability of winning the game of craps is 0. 492929 for the player. Thus the game is slightly advantageous to the house. Sharif University of Technology 34

Game Of Craps Using Biased Dice § Now assume that for each dice, - Faces 1, 2 and 3 appear with probability - Faces 4, 5 and 6 appear with probability § If T represents the combined total for the two dice, we get Sharif University of Technology 35

Game Of Craps Using Biased Dice T=k 4 pk = P{T = k} 0. 0706 5 0. 1044 6 0. 1353 7 0. 1661 8 0. 1419 9 0. 1178 10 0. 0936 11 0. 0624 § This gives the probability of win on the first throw to be § and the probability of win by throwing a carry-over to be § Thus § Although perfect dice gives rise to an unfavorable game, Sharif University of Technology 36

Game Of Craps Using Biased Dice § Even if we let the two dice to have different loading factors situation described above), similar conclusions do follow. and (for the § For example, § gives: Sharif University of Technology 37

Euler, Ramanujan and Bernoulli Numbers

Euler’s Identity § S. Ramanujan in (J. of Indian Math Soc; V, 1913): § if are numbers less than unity § where the subscripts are the series of prime numbers, then § The terms above arranged so that the product obtained by multiplying the subscripts are the series of all natural numbers § This follows by observing that the natural numbersare formed by multiplying primes and their powers. Sharif University of Technology 39

Euler’s Identity § This is used to derive a variety of interesting identities including the Euler’s identity. § By letting § This gives the Euler identity § The right side can be related to the Bernoulli numbers (for s even). § Bernoulli numbers are positive rational numbers defined through the power series expansion of the even function § Thus if we write § Then Sharif University of Technology 40

Euler’s Identity § Alse we can obtain : § This is another way to define Bernoulli numbers § Further § which gives § Thus Sharif University of Technology 41