Incremental Support Vector Machine Classification Second SIAM International

Incremental Support Vector Machine Classification Second SIAM International Conference on Data Mining Arlington, Virginia, April 11 -13, 2002 Glenn Fung & Olvi Mangasarian Data Mining Institute University of Wisconsin - Madison

Key Contributions v. Fast incremental classifier based on PSVM u Proximal Support Vector Machine v. Capable of modifying an existing linear classifier by both adding and retiring data v. Extremely simple to implement u Small memory requirement ³ Even for huge problems (1 billion) u NO optimization packages (LP, QP) needed

Outline of Talk v (Standard) Support vector machines (SVM) u Classification by halfspaces v Proximal linear support vector machines (PSVM) u Classification by proximity to planes v. The incremental and decremental algorithm u Option of keeping or retiring old data v. Numerical results u 1 Billion points in 10 dimensional space classified in less than 3 hours! u. Numerical results confirm that algorithm time is linear in the number of data points

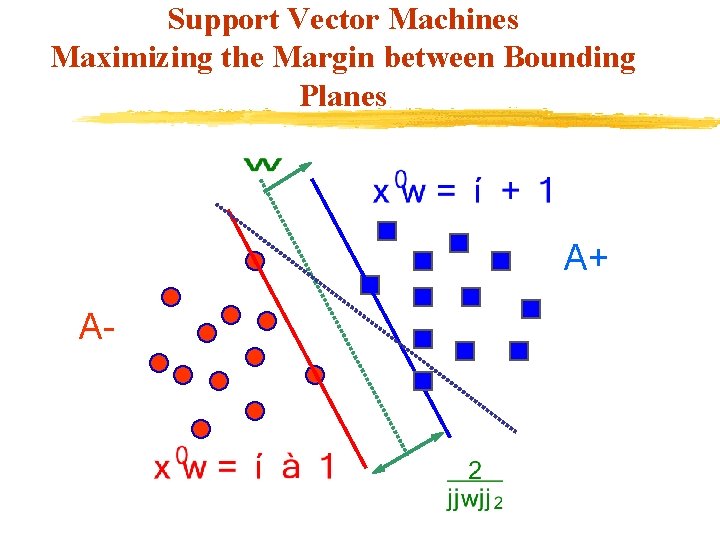
Support Vector Machines Maximizing the Margin between Bounding Planes A+ A-

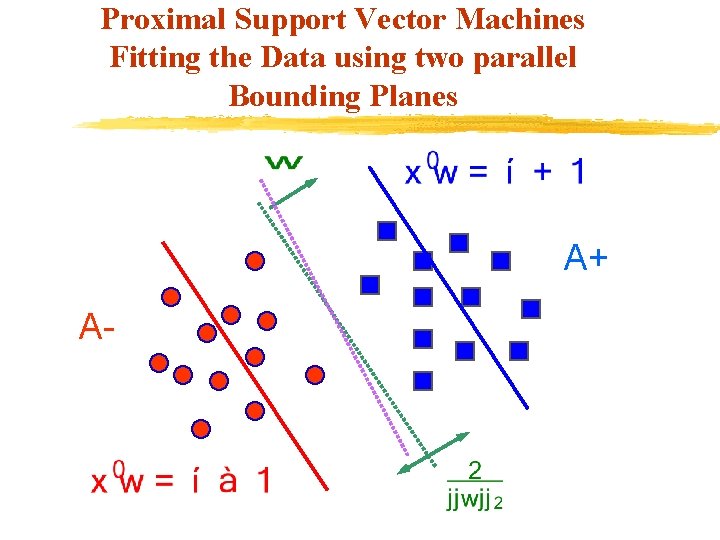
Proximal Support Vector Machines Fitting the Data using two parallel Bounding Planes A+ A-

Standard Support Vector Machine Algebra of 2 -Category Linearly Separable Case v Given m points in n dimensional space v Represented by an m-by-n matrix A v Membership of each in class +1 or – 1 specified by: v An m-by-m diagonal matrix D with +1 & -1 entries v Separate by two bounding planes, v More succinctly: where e is a vector of ones.

Standard Support Vector Machine Formulation v Solve the quadratic program for some min (QP) s. t. where : , denotes or , membership. v Margin is maximized by minimizing

PSVM Formulation We have from the standard QP SVM formulation: min (QP) s. t. Solving for in terms of and gives: min This simple, but critical modification, changes the nature of the optimization problem tremendously!!

Advantages of New Formulation v Objective function remains strongly convex. v An explicit exact solution can be written in terms of the problem data. v PSVM classifier is obtained by solving a single system of linear equations in the usually small dimensional input space. v Exact leave-one-out-correctness can be obtained in terms of problem data.

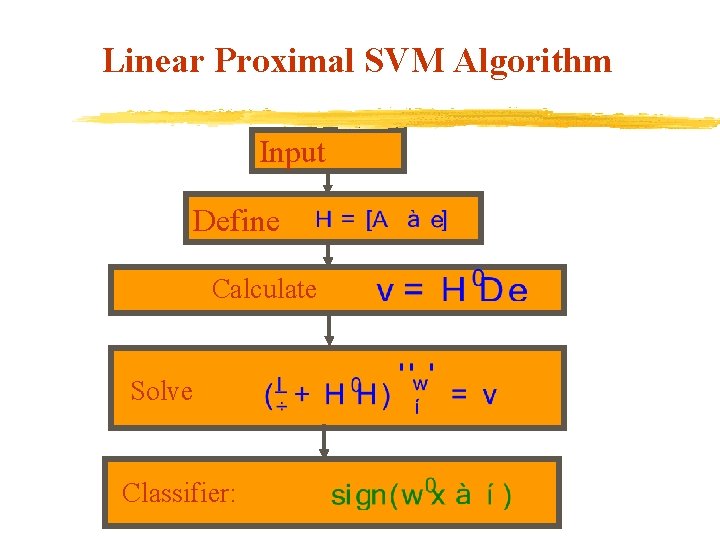
Linear PSVM v. We want to solve: min v. Setting the gradient equal to zero, gives a nonsingular system of linear equations. v. Solution of the system gives the desired PSVM classifier.

Linear PSVM Solution Here, v The linear system to solve depends on: which is of size v is usually much smaller than

Linear Proximal SVM Algorithm Input Define Calculate Solve Classifier:

Linear & Nonlinear PSVM MATLAB Code function [w, gamma] = psvm(A, d, nu) % PSVM: linear and nonlinear classification % INPUT: A, d=diag(D), nu. OUTPUT: w, gamma % [w, gamma] = psvm(A, d, nu); [m, n]=size(A); e=ones(m, 1); H=[A -e]; v=(d’*H)’ %v=H’*D*e; r=(speye(n+1)/nu+H’*H)v % solve (I/nu+H’*H)r=v w=r(1: n); gamma=r(n+1); % getting w, gamma from r

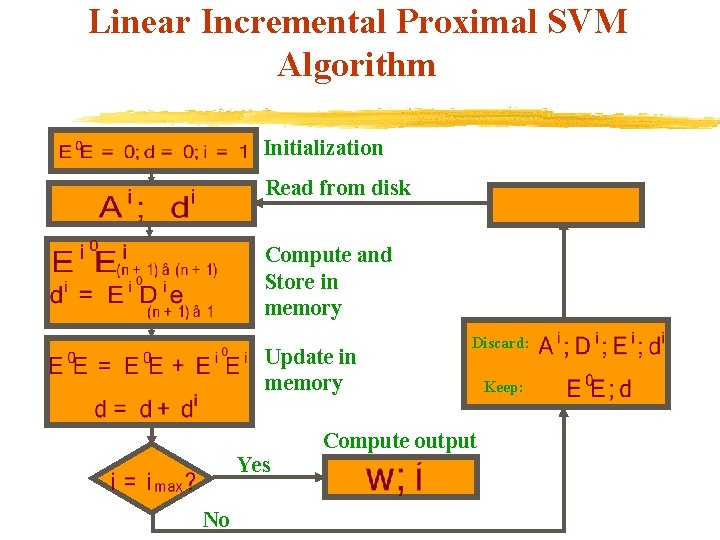
Incremental PSVM Classification v Suppose we have two “blocks” of data and v The linear system to solve depends on the compressed blocks: which are of the size

Linear Incremental Proximal SVM Algorithm Initialization Read from disk Compute and Store in memory Update in memory Yes No Discard: Compute output Keep:

Linear Incremental Proximal SVM Adding – Retiring Data v Capable of modifying an existing linear classifier by both adding and retiring data v Option of retiring old data is similar to adding new data u Financial Data: old data is obsolete v Option of keeping old data and merging it with the new data: u Medical Data: old data does not obsolesce.

Numerical experiments One-Billion Two-Class Dataset v Synthetic dataset consisting of 1 billion points in 10 dimensional input space v Generated by NDC (Normally Distributed Clustered) dataset generator v. Dataset divided into 500 blocks of 2 million points each. v. Solution obtained in less than 2 hours and 26 minutes v About 30% of the time was spent reading data from disk. v. Testing set Correctness 90. 79%

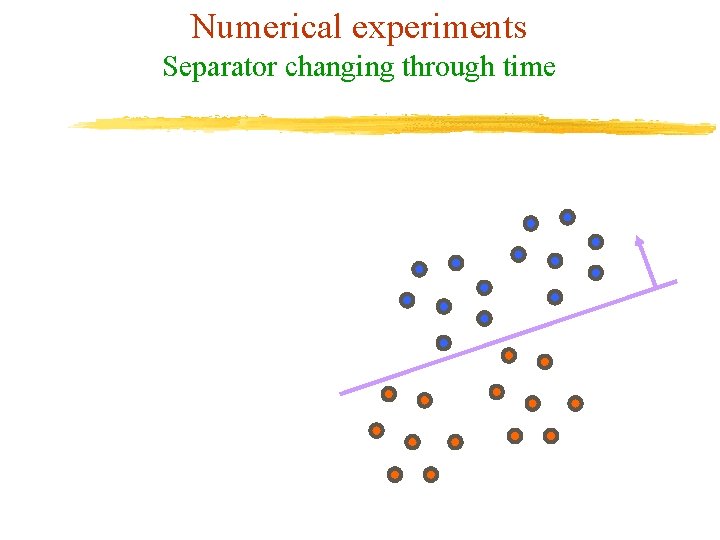
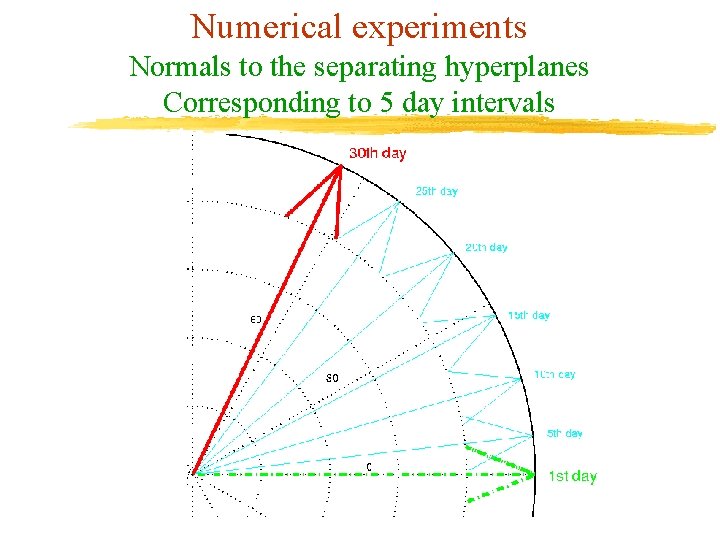
Numerical Experiments Simulation of Two-month 60 -Million Dataset v Synthetic dataset consisting of 60 million points (1 million per day) in 10 - dimensional input space v Generated using NDC v At the beginning, we only have data corresponding to the first month v Every day: u The oldest block of data is retired (1 Million) u A new block is added (1 Million) u A new linear classifier is calculated daily v Only an 11 by 11 matrix is kept in memory at the end of each day. All other data is purged.

Numerical experiments Separator changing through time

Numerical experiments Normals to the separating hyperplanes Corresponding to 5 day intervals

Conclusion v Proposed algorithm is an extremely simple procedure for generating linear classifiers in an incremental fashion for huge datasets. v The linear classifier is obtained by solving a single system of linear equations in the small dimensional input space. v The proposed algorithm has the ability to retire old data and add new data in a very simple manner. v Only a matrix of the size of the input space is kept in memory at any time

Future Work v Extension to nonlinear classification v Parallel formulation and implementation on remotely located servers for massive datasets v Real time on-line application, e. g. fraud detection