Incorporating uncertainty in distancematrix phylogenetics Wally Gilks Tom

  • Slides: 14
Download presentation
Incorporating uncertainty in distance-matrix phylogenetics Wally Gilks Tom Nye Pietro Liò Leeds University Newcastle

Incorporating uncertainty in distance-matrix phylogenetics Wally Gilks Tom Nye Pietro Liò Leeds University Newcastle University Cambridge University Isaac Newton Institute December 17, 2007

Distance-based methods • Larger trees • Faster algorithms • Less model-dependent – Genome-scale evolutionary

Distance-based methods • Larger trees • Faster algorithms • Less model-dependent – Genome-scale evolutionary rearrangements

Agglomerative distance methods • NJ (Saitou and Nei, 1987) • Bio. NJ (Gascuel, 1997)

Agglomerative distance methods • NJ (Saitou and Nei, 1987) • Bio. NJ (Gascuel, 1997) • Weighbor (Bruno et al, 2000) • MVR (Gascuel, 2000) • Fast. ME (Desper and Gascuel, 2004)

Variance models • Independent distances – Ordinary Least Squares (OLS) – Weighted Least Squares

Variance models • Independent distances – Ordinary Least Squares (OLS) – Weighted Least Squares (WLS) A – NJ, Weighbor, Fast. ME • Correlated distances – – shared evolutionary paths (Chakraborty, 1977) computed from shared sequences: Bio. NJ induced by estimation process (we show) Generalised Least Squares (GLS) – Hasegawa (1985), Bulmer (1991), MVR A B C

Two types of tree Ultrametric time tree Time (mya) Non-ultrametric divergence tree Divergence =

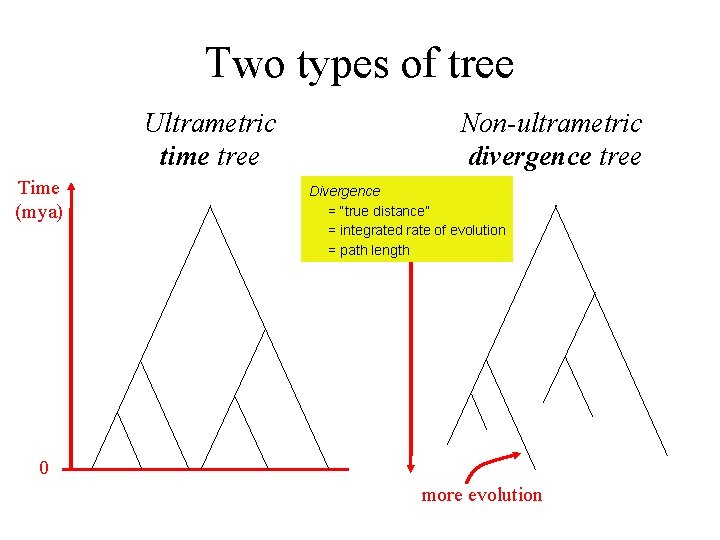
Two types of tree Ultrametric time tree Time (mya) Non-ultrametric divergence tree Divergence = “true distance” = integrated rate of evolution = path length 0 more evolution

Which tree type to assume? • • Ultrametric tree makes stronger assumptions Different methods

Which tree type to assume? • • Ultrametric tree makes stronger assumptions Different methods for estimating each type But both types are in principle correct! Our method coherently integrates both types – Produces rooted tree, no need for outgroup

An agglomerative stage time tree Time (mya) divergence tree Divergence E E 0 A

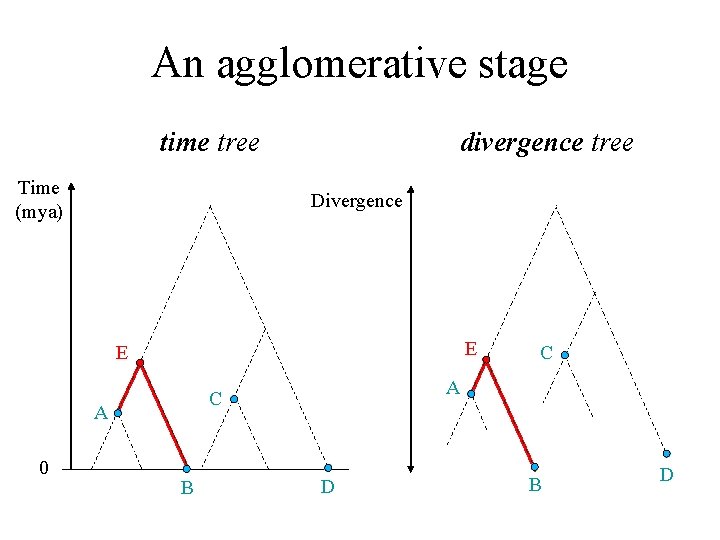
An agglomerative stage time tree Time (mya) divergence tree Divergence E E 0 A C A B C D B D

Divergence additivity divergence tree and for X = C, D, … E C A

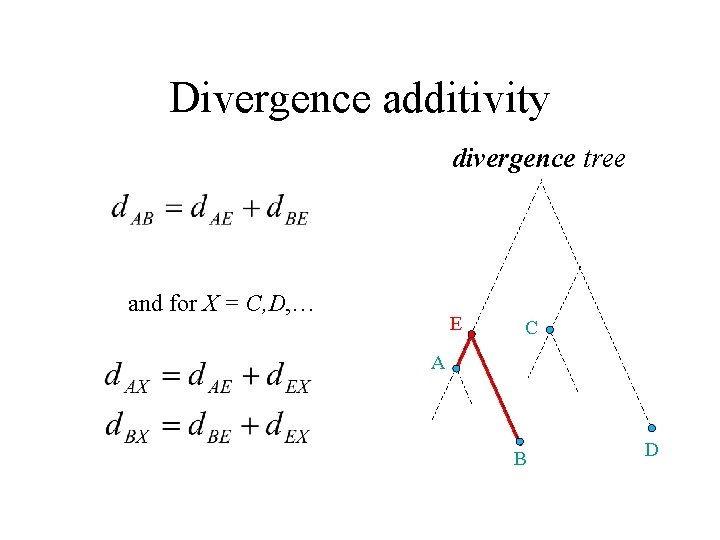
Divergence additivity divergence tree and for X = C, D, … E C A B D

Distances are estimated divergences Regression model divergence tree and for X = C, D,

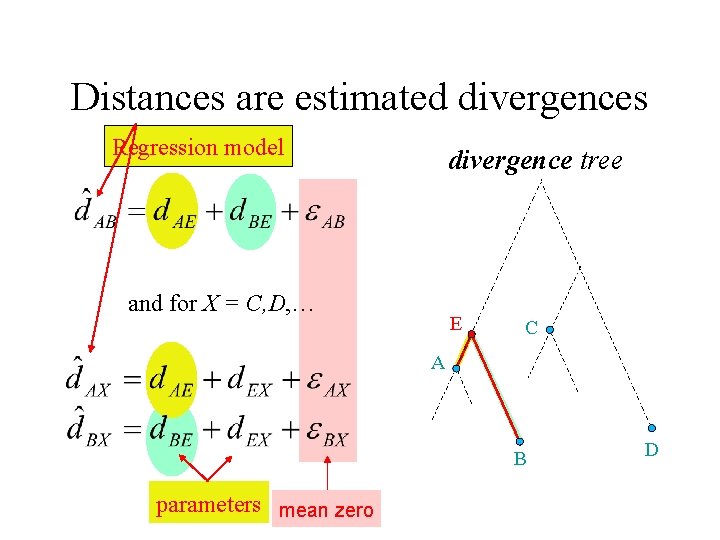
Distances are estimated divergences Regression model divergence tree and for X = C, D, … E C A B parameters mean zero D

Divergences are distorted times time tree Time (mya) E parameter mean zero uncorrelated 0

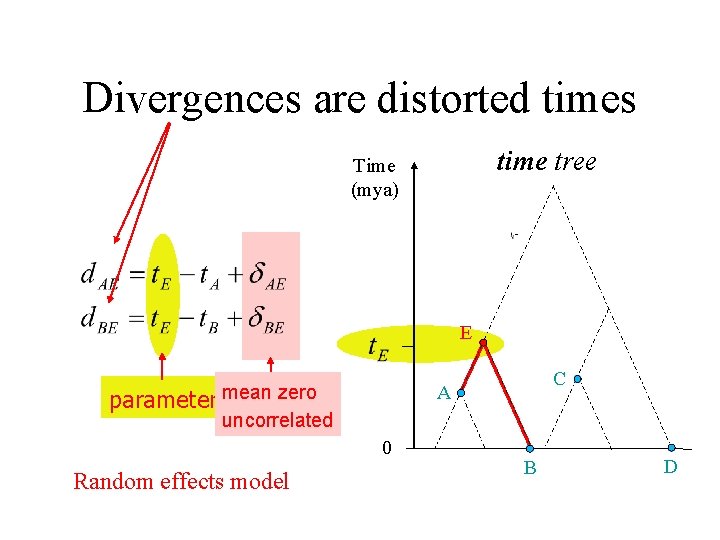
Divergences are distorted times time tree Time (mya) E parameter mean zero uncorrelated 0 Random effects model C A B D

Variance assumptions controls noise function of clade A structure clade A size shared node

Variance assumptions controls noise function of clade A structure clade A size shared node A elapsed time Chakraborty (1977) Nei et al (1985) Bulmer (1991) variance parameters controls distortion

Estimation • Time tree and divergence tree are estimated simultaneously – by GLS (Hasegawa,

Estimation • Time tree and divergence tree are estimated simultaneously – by GLS (Hasegawa, 1985; Bulmer, 1991) • Choose most recent agglomeration always • Estimated divergences become the distances for the next stage – Variance formula accommodates estimation-induced correlations

Notes • Can estimate variance parameters s 2 and n • Computationally efficient algorithm

Notes • Can estimate variance parameters s 2 and n • Computationally efficient algorithm – same time-complexity as Bio. NJ – we call it Stat. Tree

Simulations Mean topological correctness n=1% n=5% n=10% s=5% Stat. Tree = 95% Stat. Tree

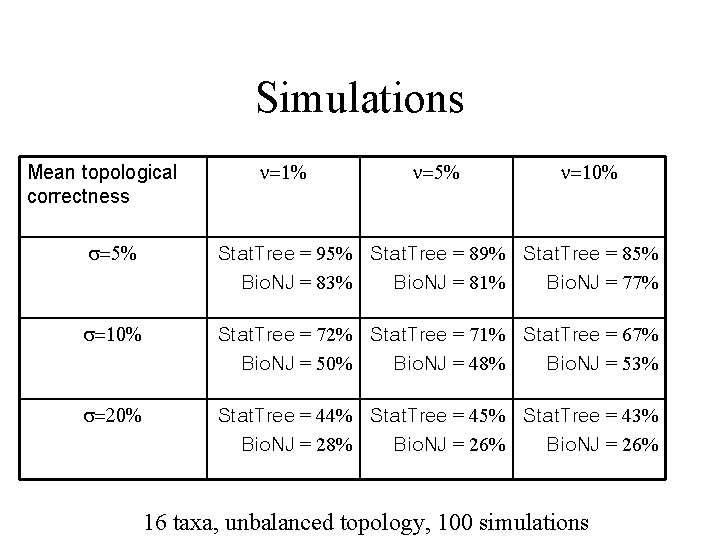
Simulations Mean topological correctness n=1% n=5% n=10% s=5% Stat. Tree = 95% Stat. Tree = 89% Stat. Tree = 85% Bio. NJ = 83% Bio. NJ = 81% Bio. NJ = 77% s=10% Stat. Tree = 72% Stat. Tree = 71% Stat. Tree = 67% Bio. NJ = 50% Bio. NJ = 48% Bio. NJ = 53% s=20% Stat. Tree = 44% Stat. Tree = 45% Stat. Tree = 43% Bio. NJ = 28% Bio. NJ = 26% 16 taxa, unbalanced topology, 100 simulations

Introduction to Phylogenetics Phylogenetics Phylogenetics is the studyIntroduction to Phylogenetics Phylogenetics Phylogenetics is the study
Wally Olins Designer Wally Olins is generally recognizedWally Olins Designer Wally Olins is generally recognized
Distance based phylogenetics Usman Roshan Phylogenetics Study ofDistance based phylogenetics Usman Roshan Phylogenetics Study of
PHYLOGENETIC ANALYSIS Phylogenetics Phylogenetics is the study ofPHYLOGENETIC ANALYSIS Phylogenetics Phylogenetics is the study of
Molecular Phylogenetics Dan Graur 1 Objectives of phylogeneticsMolecular Phylogenetics Dan Graur 1 Objectives of phylogenetics
CS 177 Phylogenetics I Taxonomy and phylogenetics PhylogeneticCS 177 Phylogenetics I Taxonomy and phylogenetics Phylogenetic
Biogeography and Phylogenetics Phylogenetics What did our phylogeneticBiogeography and Phylogenetics Phylogenetics What did our phylogenetic
Molecular phylogenetics Molecular phylogenetics fundamentals All of lifeMolecular phylogenetics Molecular phylogenetics fundamentals All of life
CS 177 Phylogenetics I Taxonomy and phylogenetics PhylogeneticCS 177 Phylogenetics I Taxonomy and phylogenetics Phylogenetic
Uncertainty Uncertainty n n n Uncertainty is aUncertainty Uncertainty n n n Uncertainty is a
Incorporating Social Media into Your Marketing Strategy IncorporatingIncorporating Social Media into Your Marketing Strategy Incorporating
INCORPORATING TECHNOLOGY IN EDUCATION ITE Incorporating Technology inINCORPORATING TECHNOLOGY IN EDUCATION ITE Incorporating Technology in
Incorporating Sources Quoting Paraphrasing and Citing 20120917 IncorporatingIncorporating Sources Quoting Paraphrasing and Citing 20120917 Incorporating