INCIDENCE GEOMETRIES Part II Further Examples and Properties

INCIDENCE GEOMETRIES Part II Further Examples and Properties

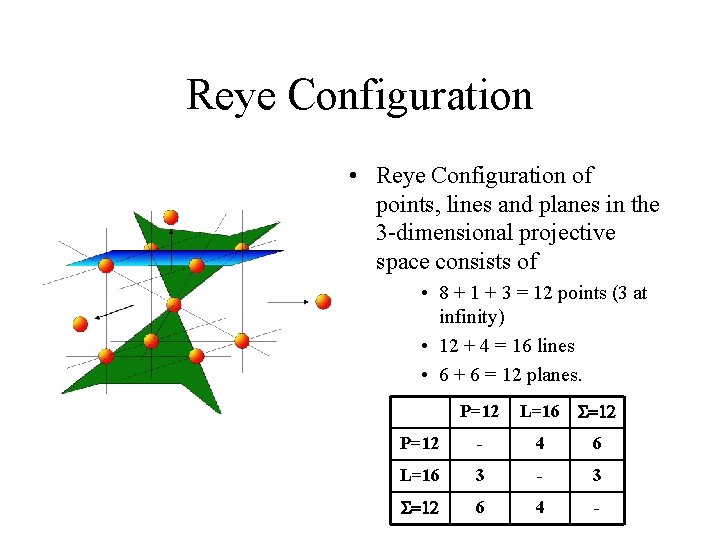
Reye Configuration • Reye Configuration of points, lines and planes in the 3 -dimensional projective space consists of • 8 + 1 + 3 = 12 points (3 at infinity) • 12 + 4 = 16 lines • 6 + 6 = 12 planes. P=12 L=16 S=12 P=12 - 4 6 L=16 3 - 3 S=12 6 4 -

Theodor Reye • Theodor Reye (1838 1919), German Geometer. • Known for his book : Geometrie der Lage (1866 in 1868). • Published this configuration in 1878. • Posed “the problem of configurations. ”

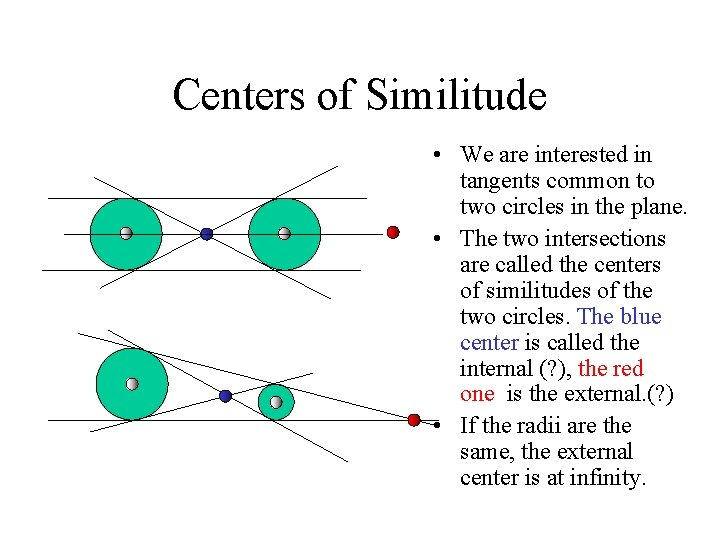
Centers of Similitude • We are interested in tangents common to two circles in the plane. • The two intersections are called the centers of similitudes of the two circles. The blue center is called the internal (? ), the red one is the external. (? ) • If the radii are the same, the external center is at infinity.

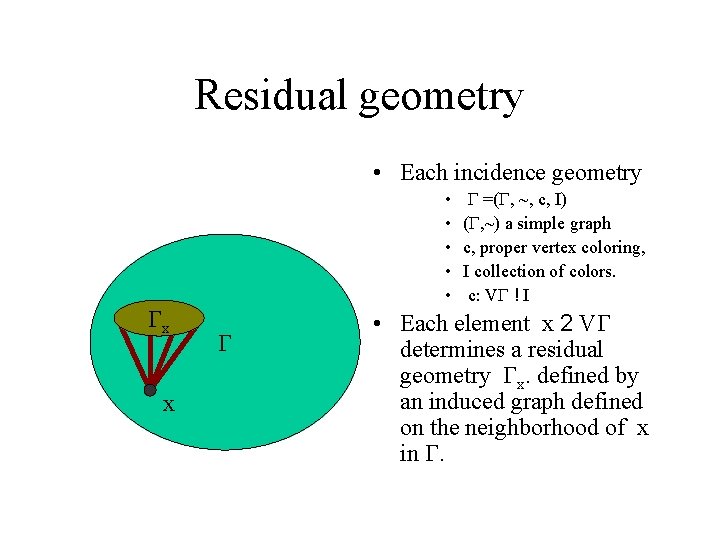
Residual geometry • Each incidence geometry Gx x • • • G G =(G, ~, c, I) (G, ~) a simple graph c, proper vertex coloring, I collection of colors. c: VG ! I • Each element x 2 VG determines a residual geometry Gx. defined by an induced graph defined on the neighborhood of x in G.

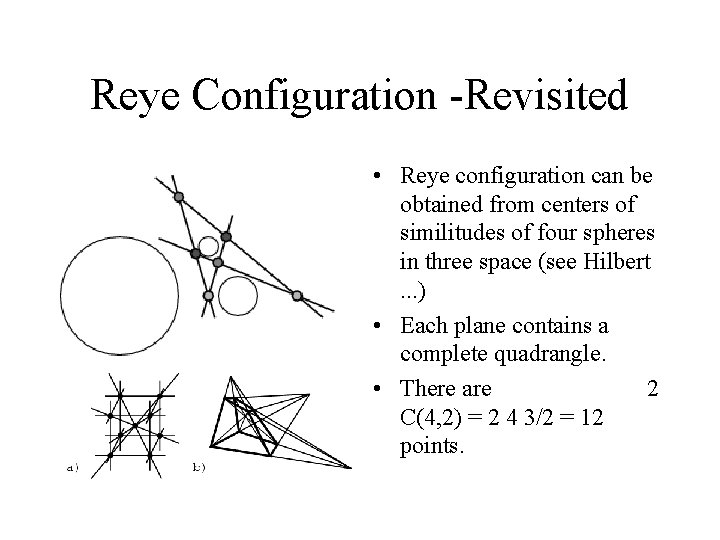
Reye Configuration -Revisited • Reye configuration can be obtained from centers of similitudes of four spheres in three space (see Hilbert. . . ) • Each plane contains a complete quadrangle. • There are 2 C(4, 2) = 2 4 3/2 = 12 points.

Exercises • N 1. Let there be three circles in a plane giving rise to 3 internal and 3 external centers of similitude. Prove that the three external center of similitude are colinear.

Flags and Residuals • In an incidence geometry G a clique on m vertices (complete subgraph) is called a flag of rank m. • Residuum can be definied for each flag F ½ V(G). G(F) = Å{G(x) = Gx |x 2 F}. • A maximal flag (flag of rank |I|} is called a chamber. A flag of rank |I|-1 is called a wall. • To each geometry G we can associate the chamber graph: • Vertices: chambers • Two chamber are adjacent if and only if they share a common wall. • (See Egon Shulte, . . . , Titts systems)

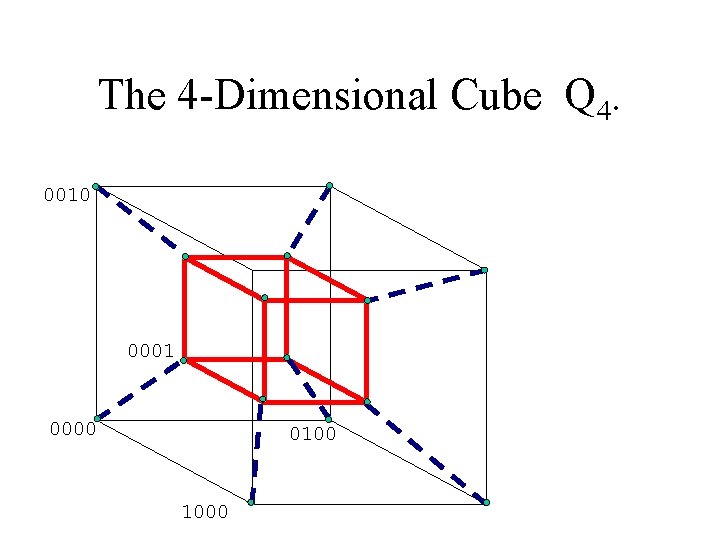
The 4 -Dimensional Cube Q 4. 0010 0001 0000 0100 1000

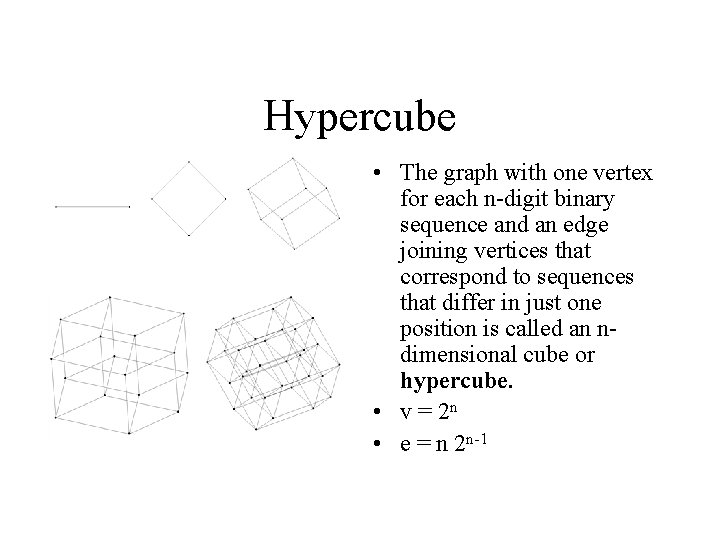
Hypercube • The graph with one vertex for each n-digit binary sequence and an edge joining vertices that correspond to sequences that differ in just one position is called an ndimensional cube or hypercube. • v = 2 n • e = n 2 n-1

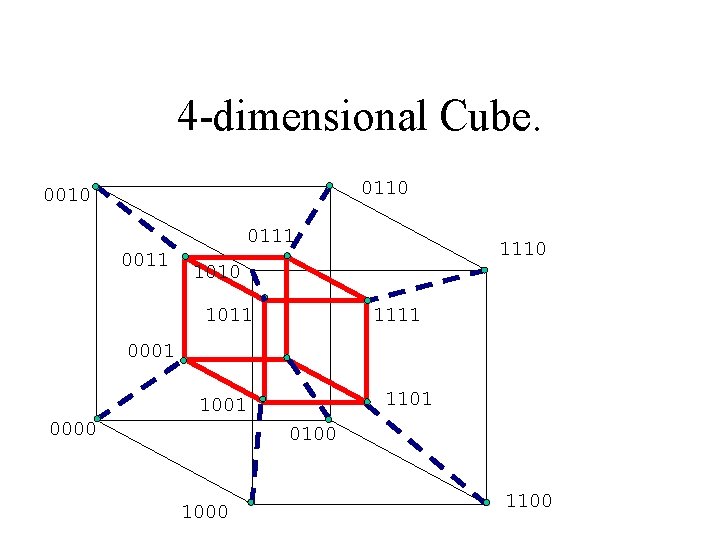
4 -dimensional Cube. 0110 0010 0111 0011 1110 1011 1111 0001 1101 1001 0000 0100 1000 1100

4 -dimensional Cube and a Famous Painting by Salvador Dali • Salvador Dali (1904 – 1998) produced in 1954 the Crucifixion (Metropolitan Museum of Art, New York) in which the cross is a 3 dimensional net of a 4 dimensional hypercube.

4 -dimensional Cube and a Famous Painting by Salvador Dali • Salvador Dali (1904 – 1998) produced in 1954 the Crucifixion (Metropolitan Museum of Art, New York) in which the cross is a 3 dimensional net of a 4 dimensional hypercube.

The Geometry of Q 4. • • • Vertices (Q 0) of Q 4: 16 Edges (Q 1)of Q 4: 32 Squares (Q 2) of Q 4: 24 Cubes (Q 3) of Q 4: 8 Total: 80 The Levi graph of Q 4 has 80 vertices and is colored with 4 colors.

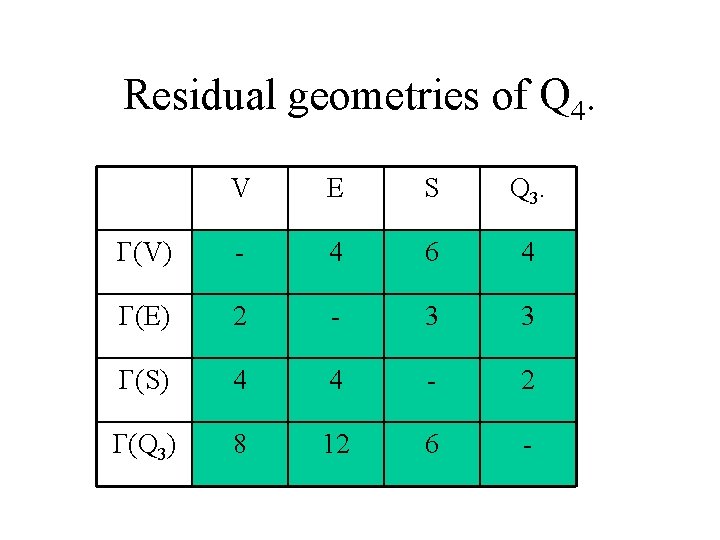
Residual geometries of Q 4. V E S Q 3. G(V) - 4 6 4 G(E) 2 - 3 3 G(S) 4 4 - 2 G(Q 3) 8 12 6 -

Exercises • N 1: Determine all residual geometries of Reyeve configuration • N 2: Determine all residual geometries of Q 4. • N 3: Determine all residual geometries of Platonic solids. • N 4: Determine the Levi graph of the geometry for the grup Z 2 £ Z 2, with three cyclic subgroups, generated by 100, 010, 001, respectively. • (Add Exercises for truncations!!!)

Posets • Let (P, ·) be a poset. We assume that we add two special (called trivial) elements, 0, and 1, such that for each x 2 P, we have 0 · x · 1.

Ranked Posets • Note that a ranked poset (P, ·) or rank n has the property that there exists a rank function r: P ! {1, 0, 1, . . . , n}, r(0) = -1, r(1) = n and if y covers x then r(y) = r(x) +1. • If we are given a poset (P, ·) with a rank function r, then such a poset defines a natural incidence geometry. • V(G) = P. • x ~ y if and only if x < y. • c(x) : = r(x). Vertex color is just the rank.

Intervals in Posets • Let (P, ·) be a poset. • Then I(x, z) = {y| x · y · z} is called the interval between x and z. • Note that I(x, z) is empty if and only if x £ z. • I(x, z) is also a ranked poset with 0 and 1.

Connected Posets. • A ranked poset (P, ·) wih 0 and 1 is called connected, if either rank(P) = 1 or for any two non-trivial elements x and y there exists a sequence x = z 0, z 1, . . . , zm = y, such that there is a path avoiding 0 and 1 in the Levi graph from x to y and rank function is changed by § 1 at each step of the path.

Abstract Polytopes • Peter Mc. Mullen and Egon Schulte define abstract polytopes as special ranked posets. • Their definition is equivalent to the following: • (P, ·) is a ranked poset with 0 and 1 (minimal and maximal element) • For any two elements x and z, such that r(z) = r(x+2), x < y there exist exactly two elements y 1, y 2 such that x < y 1 < z, x < y 2 < z. • Each nonempty interval I(x, y) is connected. • Note that abstract poytopes are a special case of posets but they form also a generalization of the convex polytopes.

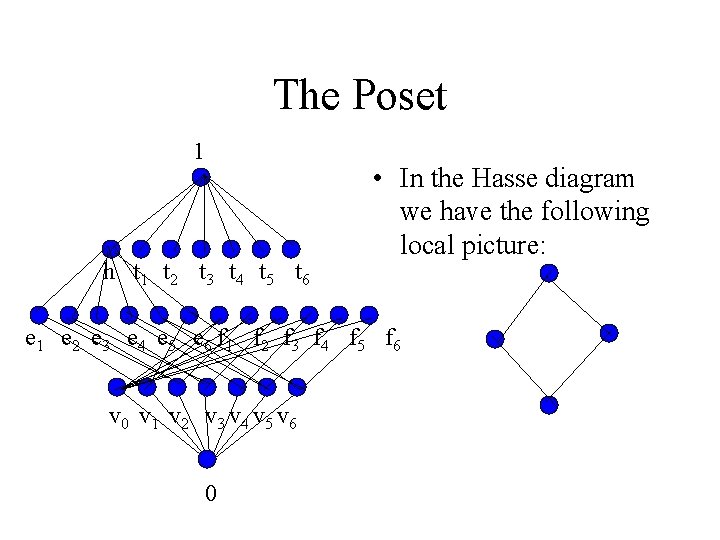
Exercises • Determine the posets and Levi graphs of each of the polytopes on the left. • Solution for the haxagonal pyramid. • 0 • 7 vertices: v 0, v 1, v 2, . . . , v 6. • 12 edges: e 1, e 2, . . . , e 6, f 1, f 2, . . . , f 6 • 7 faces: h, t 1, t 2, t 3, . . , t 6 • 1 • e 1 = v 1 v 2, e 2 = v 2 v 3, e 3 = v 3 v 4, e 4 = v 4 v 5, e 5 = v 5 v 6, e 6 = v 6 v 1, f 1 = v 1 v 0, f 2 = v 2 v 0, f 3 = v 3 v 0, f 4 = v 4 v 0, f 5=v 5 v 0, f 6 = v 6 v 0. • h = v 1 v 2 v 3 v 4 v 5 v 6, • t 1 = v 1 v 2 v 0, t 2 = v 2 v 3 v 0, t 3 = v 3 v 4 v 0, t 4 = v 4 v 5 v 0, t 5 = v 5 v 6 v 0, t 6 = v 6 v 1 v 0,

The Poset 1 h t 1 t 2 t 3 t 4 t 5 t 6 • In the Hasse diagram we have the following local picture: e 1 e 2 e 3 e 4 e 5 e 6 f 1 f 2 f 3 f 4 f 5 f 6 v 0 v 1 v 2 v 3 v 4 v 5 v 6 0