In silico Protein Design Implementing DeadEnd Elimination algorithm

In silico Protein Design: Implementing Dead-End Elimination algorithm CS 273 Tyrone Anderson, Yu Bai & Caroline E. Moore-Kochlacs May 31 st 2005

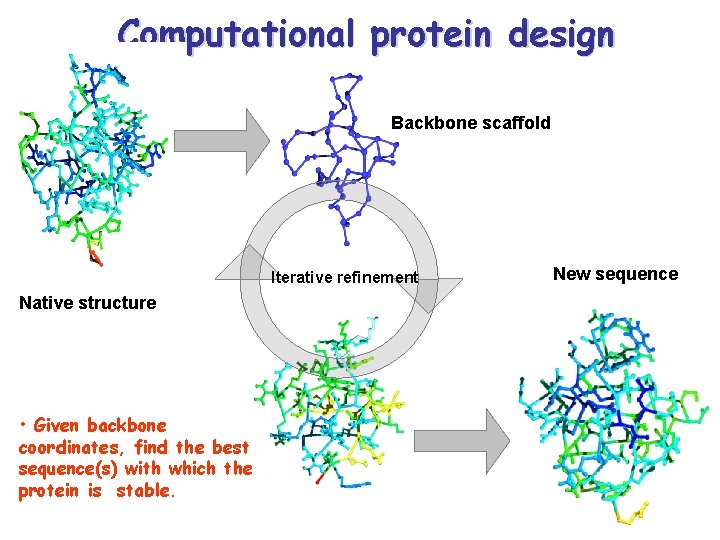
Computational protein design Backbone scaffold Iterative refinement Native structure • Given backbone coordinates, find the best sequence(s) with which the protein is stable. New sequence

Components of the problem The protein design problem can be roughly divided into searching procedure and scoring function. • The searching procedure samples the sequence space AND sidechain conformational space to create conformations. • The scoring function evaluates each conformation created by the searching procedure. The evaluation scores are used to rank the conformations (and therefore the sequences) and pick the best one to be the final model.

Why is searching procedure difficult ? • Consider a short protein with 20 amino acids. Possible sequence: S = 2020 ~1026 • Each side chain has on average 2 dihedral angles (χ angles). Assuming that we will sample every 40º in the dihedral angle space, N = (360/40)(20 2) ~1038 • This number S*N is too large to be naively sampled • Algorithms that find good solutions by screening only parts of the search space are needed

Rotamer libraries • Already in the 70 s, Janin et al. showed that different side chain conformations are not found in equal distribution over the dihedral angle space but tend to cluster at specific regions of the space, much as in the Ramachandran plot. • In the 80’s, this observation was used to improve modeling of side chain conformations. • Today, essentially all programs that model side chain conformations use rotamer libraries.

What do rotamer libraries provide? • Rotamer libraries reduce significantly the number of conformations that need to be evaluated during the search. • This is done with almost no risk of missing the real conformations. • Even small libraries of about 100 -150 rotamers cover about 9697% of the conformations actually found in protein structures. • The probabilities of each rotamer in the library can be applied to estimate the potential energy due to interactions within the side chain and with the local backbone atoms, using the Boltzmann distribution. (Not applied in this project) E ln(P)

Rotamer Library Creation • Source: – http: //honiglab. cpmc. columbia. edu/programs/sid echain/rotamers. html • Parsing: – Select all Nitrogens (N), Oxygens (O), Alpha Carbons (CA) , & all other Carbons i. e CD, CZ, etc. – Exclude all other elements and the end of file – Store in a 3 D array: Residues (1 D) Rotamers (2 D)

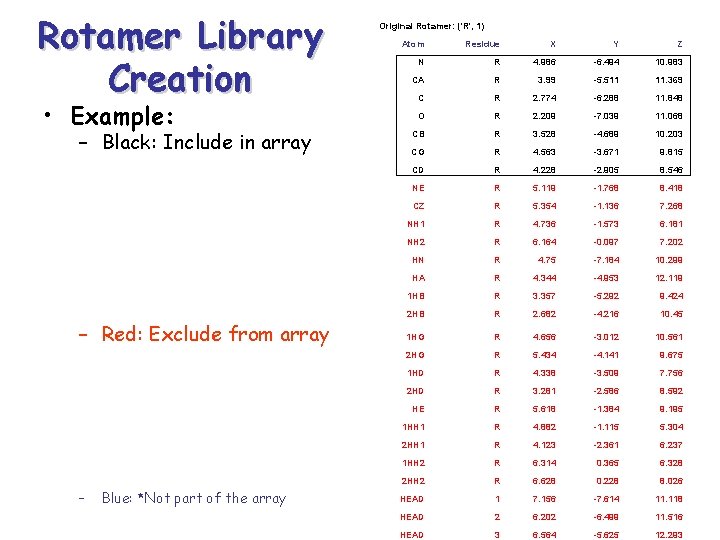
Rotamer Library Creation • Example: – Black: Include in array – Red: Exclude from array – Blue: *Not part of the array Original Rotamer: ('R', 1) Atom Residue X Y Z N R 4. 986 -6. 494 10. 983 CA R 3. 99 -5. 511 11. 369 C R 2. 774 -6. 288 11. 848 O R 2. 209 -7. 039 11. 068 CB R 3. 528 -4. 689 10. 203 CG R 4. 563 -3. 671 9. 815 CD R 4. 228 -2. 905 8. 546 NE R 5. 119 -1. 768 8. 418 CZ R 5. 354 -1. 136 7. 268 NH 1 R 4. 736 -1. 573 6. 181 NH 2 R 6. 164 -0. 097 7. 202 HN R 4. 75 -7. 184 10. 299 HA R 4. 344 -4. 953 12. 119 1 HB R 3. 357 -5. 292 9. 424 2 HB R 2. 682 -4. 216 10. 45 1 HG R 4. 656 -3. 012 10. 561 2 HG R 5. 434 -4. 141 9. 675 1 HD R 4. 338 -3. 509 7. 756 2 HD R 3. 281 -2. 586 8. 592 HE R 5. 618 -1. 384 9. 195 1 HH 1 R 4. 882 -1. 115 5. 304 2 HH 1 R 4. 123 -2. 361 6. 237 1 HH 2 R 6. 314 0. 365 6. 328 2 HH 2 R 6. 628 0. 228 8. 026 HEAD 1 7. 156 -7. 614 11. 118 HEAD 2 6. 202 -6. 499 11. 516 HEAD 3 6. 564 -5. 625 12. 293

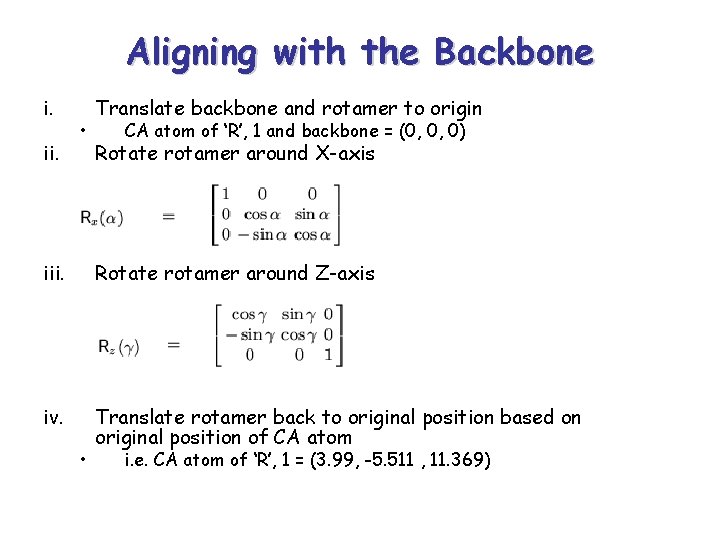
Aligning with the Backbone i. ii. • Translate backbone and rotamer to origin CA atom of ‘R’, 1 and backbone = (0, 0, 0) Rotate rotamer around X-axis iii. Rotate rotamer around Z-axis iv. Translate rotamer back to original position based on original position of CA atom • i. e. CA atom of ‘R’, 1 = (3. 99, -5. 511 , 11. 369)

Rotamer Library Manipulation • Retrieve a specific rotamer: – Provide the residue and the rotamer number • i. e. ‘R’, 1 Gives you the 1 st rotamer related to the Arginine residue • Rotamer is already aligned with the backbone • Only the coordinates of the atoms are returned in a 2 D array Aligned Rotamer: ('R', 1) 5. 0288367 -5. 67582 10. 82734 3. 99 -5. 511 11. 369 2. 7217014 -5. 64128 12. 04117 2. 1324015 -5. 76721 10. 94661 3. 50813 -5. 37317 9. 732783 4. 587644 -5. 20248 9. 188313 4. 2382361 -5. 07404 7. 407558 5. 4126639 -4. 77743 5. 614174 24. 594637 -4. 74892 15. 97595

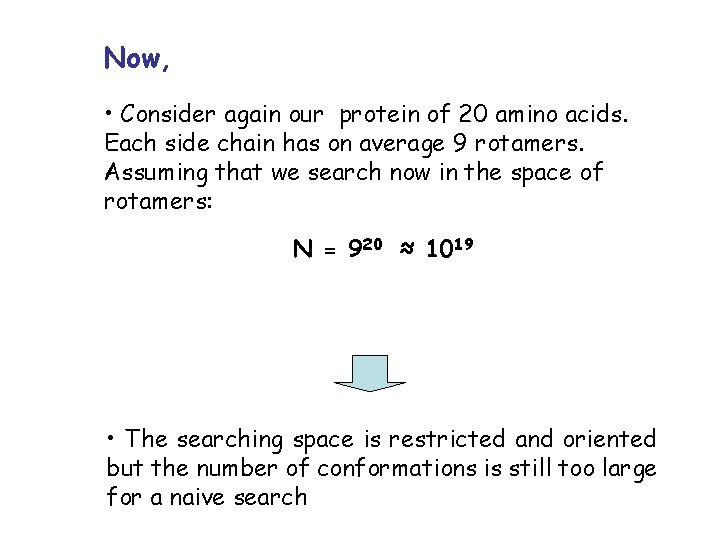
Now, • Consider again our protein of 20 amino acids. Each side chain has on average 9 rotamers. Assuming that we search now in the space of rotamers: N = 920 ≈ 1019 • The searching space is restricted and oriented but the number of conformations is still too large for a naive search

Algorithms in searching (side-chain) conformational space • Greed search (systematically scans the search space) • DEE (Algorithmic approaches to reduce the search space) • Self consistent algorithms (iterative sequential procedure) • Monte Carlo algorithms (random search)

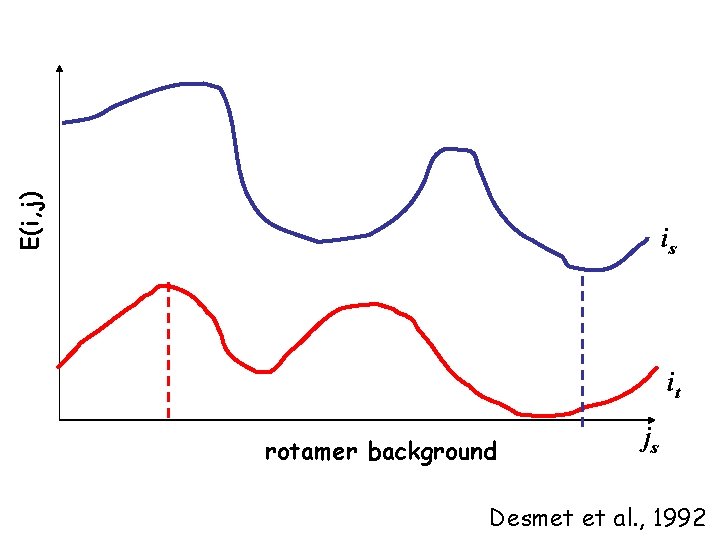
DEE (Dead-End Elimination) Aims to safely eliminates (clusters of) rotamers without loosing the GMEC (Global Minimum Energy Conformation). rotamer ir in force field of backbone only rotamer ir with rotamer(s) of other residues • Given residue i, eliminate a rotamer ir if the minimum energy it can obtain by interaction with conformational background (js) is higher (worse) than the maximum possible energy that another rotamer it (of the same residue) can have

E(i, j) is it rotamer background js Desmet et al. , 1992

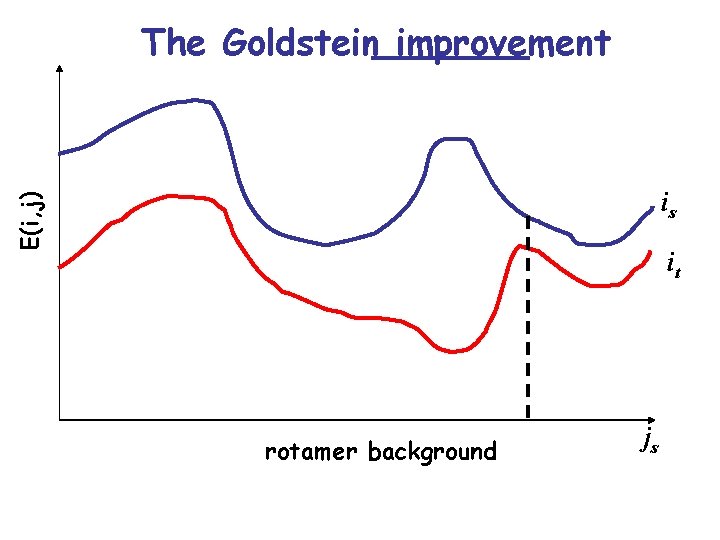
The Goldstein improvement • Rotamer ir can be safely eliminated when some other rotamer it exists with lower (better) energy for a certain environment that mostly favors ir. • This criteria is much less restrictive and therefore more powerful. It requires though more computational time.

The Goldstein improvement E(i, j) is it rotamer background js

Scoring function: Energy function Terms: • Van der Waals – represents packing specificity • Hydrogen bonding – typically represented by an angle dependent, 12 -10 hydrogen bond potential • Electrostatics – Guard against destabilizing interactions between like charged residues • Internal coordinate terms – ‘bonded’ energies • Solvation energy – Protein-solvent interactions • Entropy – Assumes conformational space is completely restricted in the folded state Gordon et al, 1999

Scoring function: Energy function Terms: • Van der Waals – represents packing specificity • Hydrogen bonding – typically represented by an angle dependent, 12 -10 hydrogen bond potential • Electrostatics – Guard against destabilizing interactions between like charged residues • Internal coordinate terms – ‘bonded’ energies • Solvation energy – Protein-solvent interactions • Entropy – Assumes conformational space is completely restricted in the folded state Gordon et al, 1999

Van der Waals • Interaction between two uncharged atoms – Mildly attractive as two atoms approach from a distance – Repulsive as they approach too close • Represents packing specificity • Prefers native-like folded states with wellorganized cores over disordered or moltenglobule states Gordon et al, 1999

Van der Waals http: //employees. csbsju. edu/hjakubowski/classes/ch 331/protstructure/ilennardjones 2. gif • 12 -6 Lennard-Jones potential – Standard approximation • R = distance between atoms • R 0 = van der Waals radii • Dij = well depth – Variation from Kuhlman and Baker, 2004 • Erep is dampened to account for the fixed backbone and rotamer set being used.

Electrostatics • Stability – Moderate temperatures: favorable electrostatic interactions not thought to be strong enough to compensate for the energy of desolvation – Extreme conditions: salt bridges may stabilize • Specificity – folding and functional interactions – maybe the more significant role of electrostatics • Currently, term guards against destabilizing interactions between like-charged residues Gordon et al, 1999

Electrostatics • Approximations: – Coulomb’s Law (Gordon et al, 1999) • Qi, Qj = charge on amino acid • R = distance • ε= dielectric constant = 40 – Bayesian version (Kuhlman & Baker, 2004) • Probability of two amino acids close together given environment and distance (from PDB) • aa=amino acid, d = distance, env =environment

Solvation • Hydrophobic effects drive folding, modeling solvation effects is critical to a protein design force field • Computationally expensive • Solvent model from Lazaridis and Karplus, 1999 – dij = distance between atoms, rij = van der Waals radii, Vi = atomic volume – ΔGref = reference solvation free energy, ΔGfree = solvation free energy of free (isolated) group – λ = correlation length

Energy Function: Incomplete model • Current standard models include Bayesian terms based on PDB statistics • Several terms have not been thoroughly validated as useful for design (Gordon et al, 1999) – Hydrogen bonding – Electrostatics – Internal coordinates • Current standard models are ad hoc, physical quantities and variables are weighted based on “what works best”

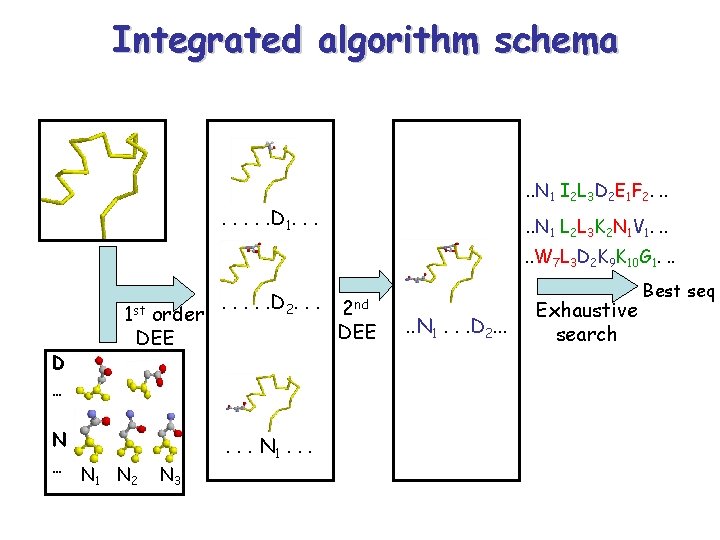
Integrated algorithm schema . . N 1 I 2 L 3 D 2 E 1 F 2. . . . D 1. . . N 1 L 2 L 3 K 2 N 1 V 1. . . W 7 L 3 D 2 K 9 K 10 G 1. . . D … 1 st order DEE N … N N 1 2 N 3 . . . D 2. . . N 1. . . 2 nd DEE . . N 1. . . D 2. . . Exhaustive search Best seq

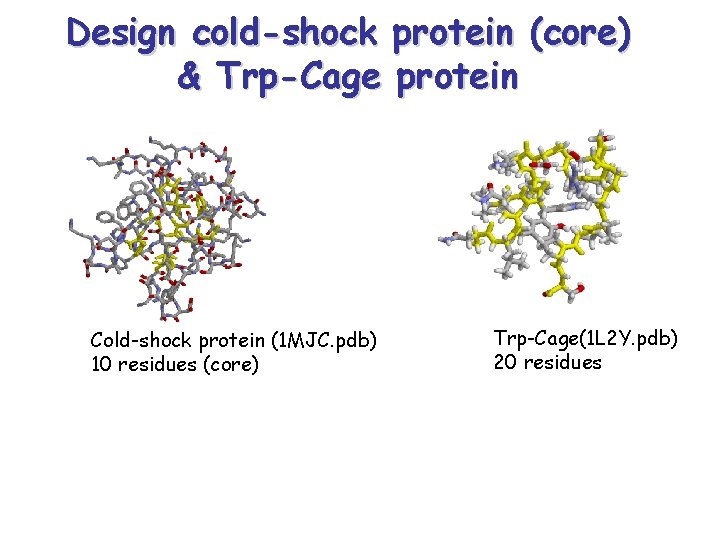
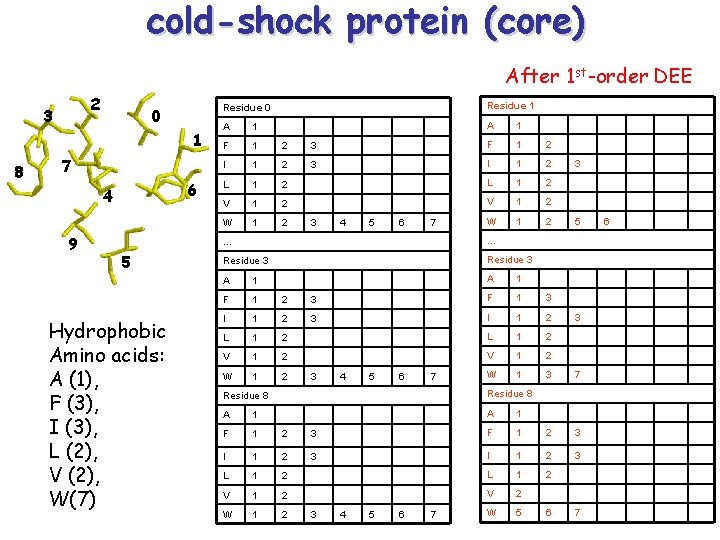
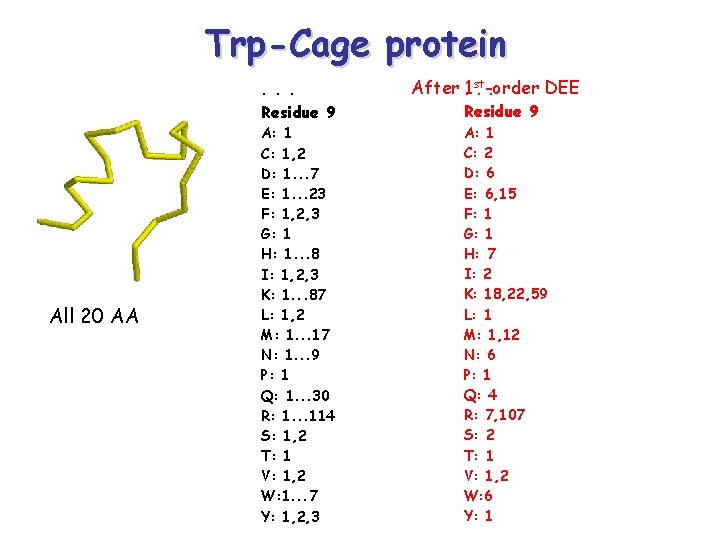
Design cold-shock protein (core) & Trp-Cage protein Cold-shock protein (1 MJC. pdb) 10 residues (core) Trp-Cage(1 L 2 Y. pdb) 20 residues

cold-shock protein (core) After 1 st-order DEE 2 3 0 1 8 7 6 4 9 5 Hydrophobic Amino acids: A (1), F (3), I (3), L (2), V (2), W(7) Residue 0 Residue 1 A 1 F 1 2 3 F 1 2 I 1 2 3 I 1 2 L 1 2 V 1 2 W 1 2 3 4 5 6 7 3 5 … … Residue 3 A 1 F 1 2 3 F 1 3 I 1 2 L 1 2 V 1 2 W 1 3 7 3 4 5 6 7 3 Residue 8 A 1 F 1 2 3 I 1 2 3 L 1 2 V 2 W 1 2 W 5 3 4 5 6 7 6

Trp-Cage protein. . . Residue 9 All 20 AA A: 1 C: 1, 2 D: 1. . . 7 E: 1. . . 23 F: 1, 2, 3 G: 1 H: 1. . . 8 I: 1, 2, 3 K: 1. . . 87 L: 1, 2 M: 1. . . 17 N: 1. . . 9 P: 1 Q: 1. . . 30 R: 1. . . 114 S: 1, 2 T: 1 V: 1, 2 W: 1. . . 7 Y: 1, 2, 3 After. 1 st DEE. -order. Residue 9 A: 1 C: 2 D: 6 E: 6, 15 F: 1 G: 1 H: 7 I: 2 K: 18, 22, 59 L: 1 M: 1, 12 N: 6 P: 1 Q: 4 R: 7, 107 S: 2 T: 1 V: 1, 2 W: 6 Y: 1

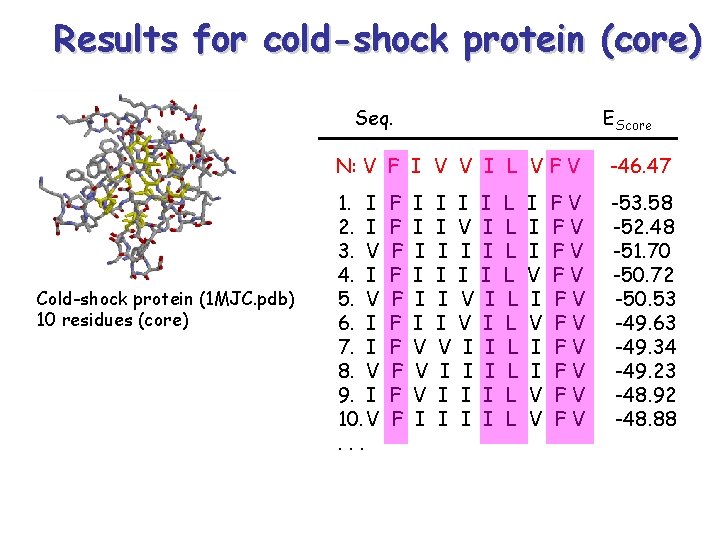
Results for cold-shock protein (core) Seq. Cold-shock protein (1 MJC. pdb) 10 residues (core) EScore N: V F I V V I L V F V -46. 47 1. I 2. I 3. V 4. I 5. V 6. I 7. I 8. V 9. I 10. V. . . -53. 58 -52. 48 -51. 70 -50. 72 -50. 53 -49. 63 -49. 34 -49. 23 -48. 92 -48. 88 F F F F F I I I V V V I I I I V I I V V I I I I L L L L L I I I V V FV FV FV

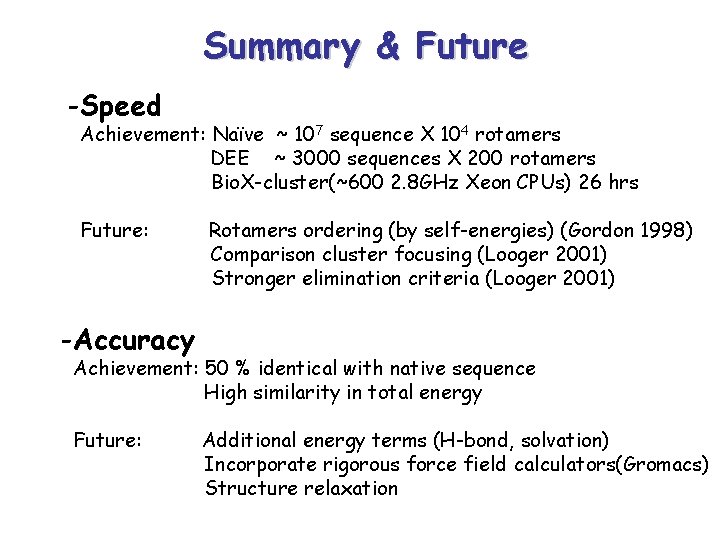
Summary & Future -Speed Achievement: Naïve ~ 107 sequence X 104 rotamers DEE ~ 3000 sequences X 200 rotamers Bio. X-cluster(~600 2. 8 GHz Xeon CPUs) 26 hrs Future: Rotamers ordering (by self-energies) (Gordon 1998) Comparison cluster focusing (Looger 2001) Stronger elimination criteria (Looger 2001) -Accuracy Achievement: 50 % identical with native sequence High similarity in total energy Future: Additional energy terms (H-bond, solvation) Incorporate rigorous force field calculators(Gromacs) Structure relaxation

Thanks !